Нахождение объема пирамиды: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.
Формула вычисления объема пирамиды
1. Общая формула
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.
- ABCD – основание;
- E – вершина;
- h – высота, перпендикулярная основанию.
2. Объем правильной треугольной пирамиды
Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):
Подставляем данное выражение в формулу расчета объема фигуры и получаем:
3. Объем правильной четырехугольной пирамиды
Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a 2 , где а – длина его стороны.
Следовательно, формулу объема можно представить в виде:
4. Объем правильной шестиугольной пирамиды
Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):
С учетом этого, объем фигуры считается так:
Примеры задач
Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:
Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.
Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см 2 (3 см ⋅ 3 см). Следовательно, объем равен:
Объем треугольной пирамиды. Формулы и пример решения задачи
Главной характеристикой любой геометрической фигуры в пространстве является ее объем. В данной статье рассмотрим, что собой представляет пирамида с треугольником в основании, а также покажем, как находить объем треугольной пирамиды – правильной полной и усеченной.
Что это – треугольная пирамида?
Каждый слышал о древних египетских пирамидах, тем не менее они являются четырехугольными правильными, а не треугольными. Объясним, как получить треугольную пирамиду.
Возьмем произвольный треугольник и соединим все его вершины с некоторой одной точкой, расположенной вне плоскости этого треугольника. Образованная фигура будет называться треугольной пирамидой. Она показана на рисунке ниже.
Вам будет интересно: Кашмирский конфликт: участники, причины, ход событий
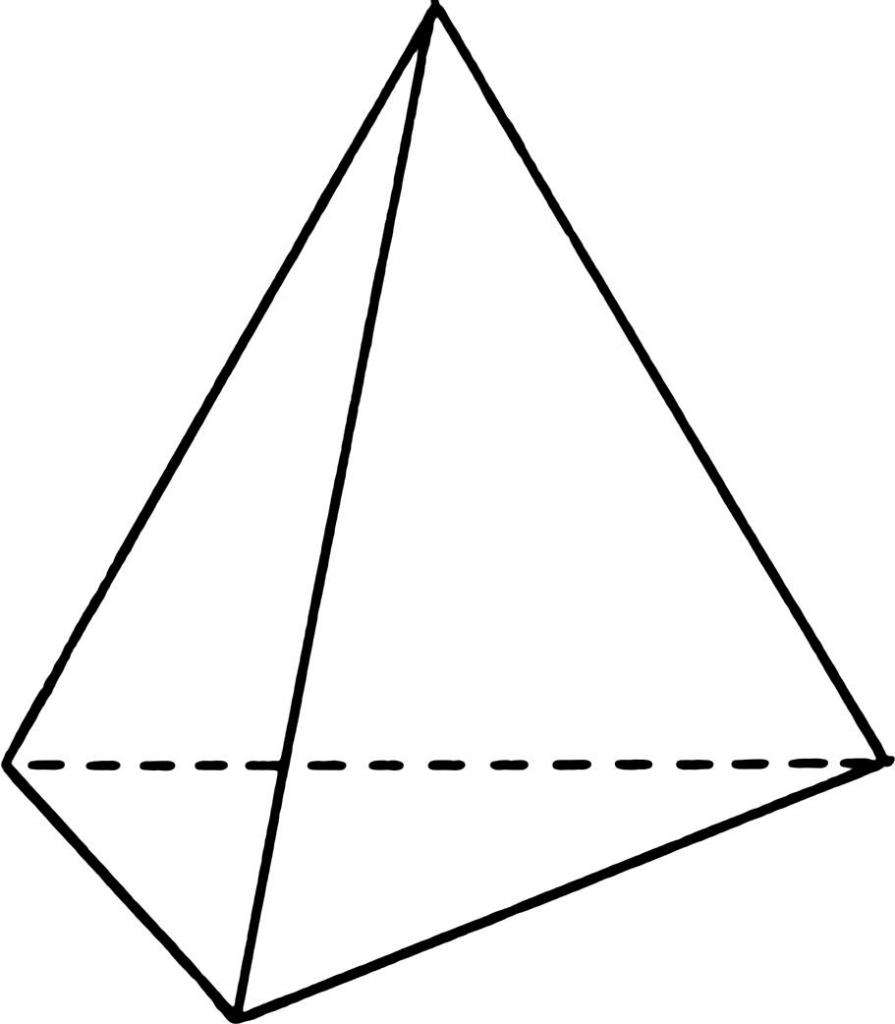
Как видно, рассматриваемая фигура образована четырьмя треугольниками, которые в общем случае являются разными. Каждый треугольник – это стороны пирамиды или ее грань. Эту пирамиду часто называют тетраэдром, то есть четырехгранной объемной фигурой.
Помимо сторон, пирамида также обладает ребрами (их у нее 6) и вершинами (их 4).
Правильная пирамида с треугольным основанием
Фигура, которая получена с использованием произвольного треугольника и точки в пространстве, будет неправильной наклонной пирамидой в общем случае. Теперь представим, что исходный треугольник имеет одинаковые стороны, а точка пространства расположена точно над его геометрическим центром на расстоянии h от плоскости треугольника. Построенная с использованием этих исходных данных пирамида будет правильной.
Очевидно, что число ребер, сторон и вершин у правильной треугольной пирамиды будет таким же, как у пирамиды, построенной из произвольного треугольника.
Однако правильная фигура обладает некоторыми отличительными чертами:
- ее высота, проведенная из вершины, точно пересечет основание в геометрическом центре (точка пересечения медиан);
- боковая поверхность такой пирамиды образована тремя одинаковыми треугольниками, которые являются равнобедренными или равносторонними.
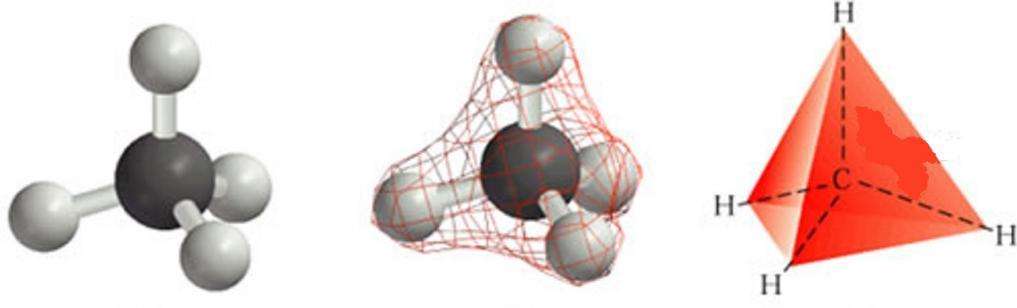
Правильная треугольная пирамида является не только чисто теоретическим геометрическим объектом. Некоторые структуры в природе имеют ее форму, например кристаллическая решетка алмаза, где атом углерода соединен с четырьмя такими же атомами ковалентными связями, или молекула метана, где вершины пирамиды образованы атомами водорода.
Формулы объема треугольной пирамиды
Определить объем совершенно любой пирамиды с произвольным n-угольником в основании можно с помощью следующего выражения:
Здесь символ So обозначает площадь основания, h – это высота фигуры, проведенная к отмеченному основанию из вершины пирамиды.
Поскольку площадь произвольного треугольника равна половине произведения длины его стороны a на апофему ha, опущенную на эту сторону, то формула объема треугольной пирамиды может быть записана в следующем виде:
V = 1/6 × a × ha × h
Для треугольной пирамиды общего типа определение высоты является непростой задачей. Для ее решения проще всего воспользоваться формулой расстояния между точкой (вершиной) и плоскостью (треугольным основанием), представленной уравнением общего вида.
Для правильной пирамиды формула объема имеет конкретный вид. Площадь основания (равностороннего треугольника) для нее равна:
Подставляем ее в общее выражение для V, получаем:
Частным случаем является ситуация, когда у тетраэдра все стороны оказываются одинаковыми равносторонними треугольниками. В этом случае определить его объем можно, только исходя из знания параметра его ребра a. Соответствующее выражение имеет вид:
Усеченная пирамида
Если верхнюю часть, содержащую вершину, отсечь у правильной треугольной пирамиды, то получится усеченная фигура. В отличие от исходной она будет состоять из двух равносторонних треугольных оснований и трех равнобедренных трапеций.
Ниже на фото показано, как выглядит правильная усеченная пирамида треугольная, изготовленная из бумаги.
Для определения объема треугольной пирамиды усеченной необходимо знать три ее линейных характеристики: каждую из сторон оснований и высоту фигуры, равную расстоянию между верхним и нижним основаниями. Соответствующая формула для объема записывается так:
V = √3/12 × h × (A2 + a2 + A × a)
Здесь h – высота фигуры, A и a – длины сторон большого (нижнего) и малого (верхнего) равносторонних треугольников соответственно.
Решение задачи
Чтобы приведенная информация в статье была понятнее для читателя, покажем на наглядном примере, как пользоваться некоторыми из записанных формул.
Пусть объем треугольной пирамиды равен 15 см3. Известно, что фигура является правильной. Следует найти апофему ab бокового ребра, если известно, что высота пирамиды составляет 4 см.
Поскольку известны объем и высота фигуры, то можно воспользоваться соответствующей формулой для вычисления длины стороны ее основания. Имеем:
a = 12 × V / (√3 × h) = 12 × 15 / (√3 × 4) = 25,98 см
Апофему ab можно рассчитать, если рассмотреть соответствующий прямоугольный треугольник внутри пирамиды. Катетами треугольника являются 1/3 длины высоты основания и высота пирамиды, гипотенузой будет искомая апофема. Тогда:
ab = √(h2 + a2 / 12) = √(16 + 25,982 / 12) = 8,5 см
Рассчитанная длина апофемы фигуры получилась больше ее высоты, что справедливо для пирамиды любого типа.
Объем треугольной пирамиды
Многогранник, в основании которого лежит правильный треугольник, а остальные грани представлены равнобедренными треугольниками называется треугольной пирамидой. Еще такую пирамиду называют тетраэдром. 
Правильная пирамида обладает множеством свойств, которые выводятся из составляющих ее фигур:
- Все стороны основания равны между собой, потому что оно представлено правильным треугольником;
- Все ребра пирамиды также равны между собой;
- Т.к. каждая грань образует равнобедренный треугольник, в котором ребра равны и основания равны, то можно сказать, что площадь каждой грани одинакова;
- Все двугранные углы при основании равны.
Площадь треугольной пирамиды рассчитывается, как сумма площадей основания и боковой развертки. Также ее можно найти, если рассчитать площадь одной из боковых граней и основания. Формула объема треугольной пирамиды также выводится из свойств треугольников, из которых она состоит:
Площадь основания рассчитывается из формулы площади правильного треугольника: 
Рассмотрим пример расчета объема треугольной пирамиды.
Используя эту формулу, важно строго следить за подсчетами и сокращениями. Одна маленькая ошибка может привести к неверному результату. В целом, найти объем правильной треугольной пирамиды очень просто.
[spoiler title=”источники:”]
http://24simba.ru/zdorove-i-bezopasnost/6384-obem-treugolnoj-piramidy-formuly-i-primer-reshenija-zadachi/
http://2mb.ru/matematika/geometriya/obem-treugolnoj-piramidy/
[/spoiler]
a – сторона куба
Формула объема куба, (V):
a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
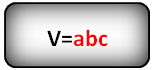
R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):
R – радиус основания
H – высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
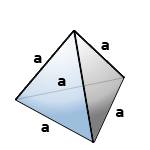
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
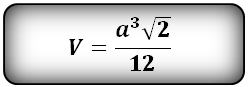
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
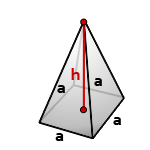
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
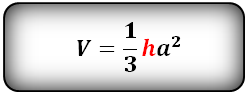
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
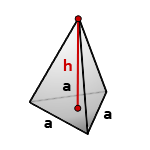
a – сторона основания
h – высота пирамиды
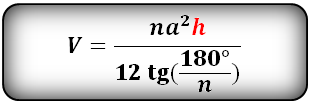
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
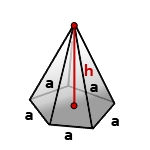
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
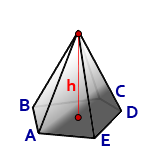
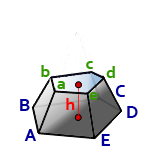
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
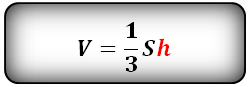
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
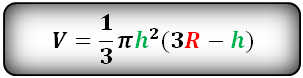
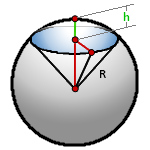
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):
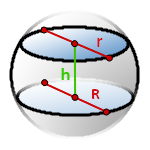
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
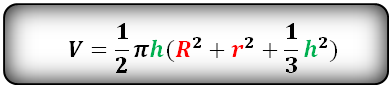
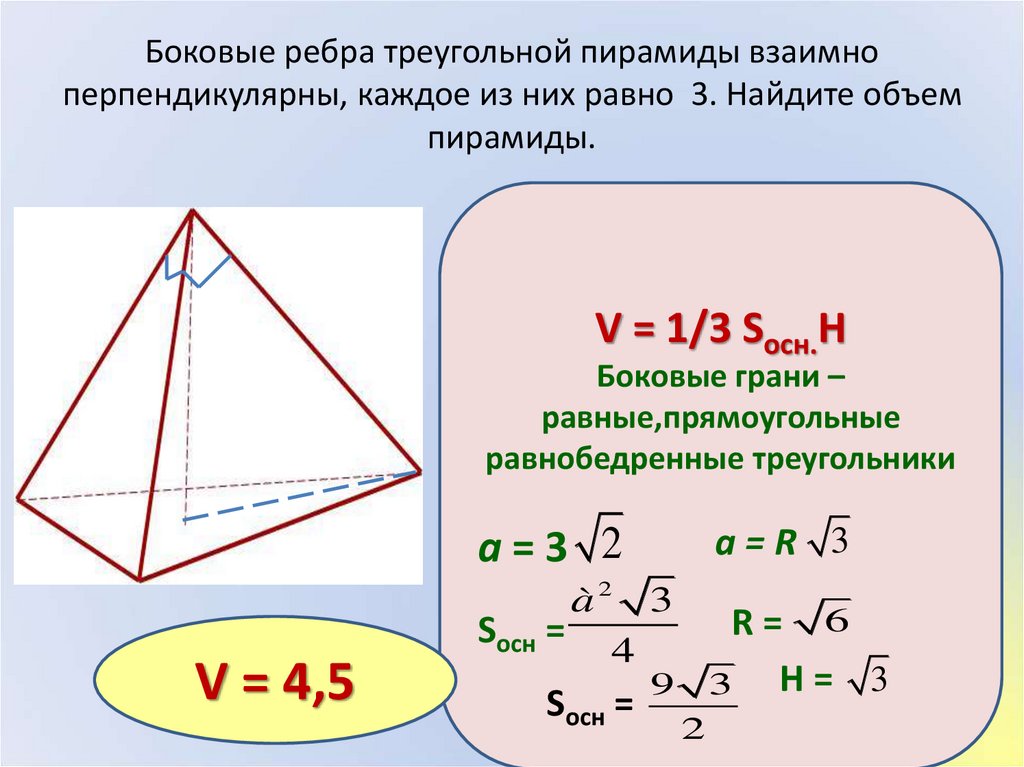
Объем правильной треугольной пирамиды
Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle H).
( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).
Вспомним, как искать эту площадь. Используем формулу площади:
( displaystyle S=frac{1}{2}abcdot sin gamma ).
У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» — это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).
Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).
Теперь найдем ( displaystyle H).
По теореме Пифагора для ( displaystyle Delta SOC)
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}).
Чему же равно ( displaystyle OC)? Это радиус описанной окружности в ( displaystyle Delta ABC), потому что пирамидаправильная и, значит, ( displaystyle O) — центр ( displaystyle Delta ABC).
Найдем ( displaystyle OC) (Подробнее смотри в теме «Правильный треугольник»).
( displaystyle OC=frac{2}{3}CK), так как ( displaystyle O) — точка пересечения и медиан тоже.
( displaystyle C{{K}^{2}}=A{{C}^{2}}-A{{K}^{2}}) (теорема Пифагора для ( displaystyle Delta ACK))
( displaystyle C{{K}^{2}}-{{a}^{2}}-frac{{{a}^{2}}}{4}=frac{3{{a}^{2}}}{4}); ( displaystyle CK=frac{asqrt{3}}{2})
Значит, ( displaystyle OC=frac{2}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{3})
Подставим ( displaystyle OC) в формулу для ( displaystyle H).
( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}={{b}^{2}}-{{left( frac{asqrt{3}}{3} right)}^{2}}={{b}^{2}}-frac{{{a}^{2}}}{3})
И подставим все в формулу объема:
( displaystyle V=frac{1}{3}{{S}_{ABC}}cdot H=frac{1}{3}cdot frac{{{a}^{2}}sqrt{3}}{4}cdot sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}})
( displaystyle V=frac{{{a}^{2}}sqrt{3}}{12}sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}}).
Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:
( displaystyle V=frac{{{a}^{3}}}{6sqrt{2}}).
формула для правильной треугольной и четырехугольной
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение объема пирамиды: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема пирамиды
- 1. Общая формула
- 2. Объем правильной треугольной пирамиды
- 3. Объем правильной четырехугольной пирамиды
- 4. Объем правильной шестиугольной пирамиды
- Примеры задач
Формула вычисления объема пирамиды
1. Общая формула
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.
- ABCD – основание;
- E – вершина;
- h – высота, перпендикулярная основанию.
2. Объем правильной треугольной пирамиды
Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):
Подставляем данное выражение в формулу расчета объема фигуры и получаем:
3.
Объем правильной четырехугольной пирамиды
Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a2, где а – длина его стороны.
Следовательно, формулу объема можно представить в виде:
4. Объем правильной шестиугольной пирамиды
Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):
С учетом этого, объем фигуры считается так:
Примеры задач
Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:
Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.
Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см2 (3 см ⋅ 3 см). Следовательно, объем равен:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Объем треугольной призмы Калькулятор | Вычислить Объем треугольной призмы
|
✖Длина — это измерение или протяженность чего-либо от конца до конца. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
|
|
✖Высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего прямо. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
|
|
✖Основание — это самая нижняя часть или край чего-либо, особенно та часть, на которой оно опирается или поддерживается. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
ⓘ Длина [L]
ⓘ Высота [h]
ⓘ Основание [b]|
✖Объем — это количество пространства, которое занимает вещество или объект или которое заключено в контейнере. |
Акр-футАкр-фут (исследование США)Акко-дюймовыйБочка (масло)Бочка (UK)Ствол (США)Ванна (библейский)Совет для ногКабина (библейский)СантилитрКентум кубический футКор (библейский)шнурКубический Ангстремкубический сантиметркубический дециметркубический футкубический дюймКилометры CubicКубический метрКубический Mileкубический миллиметркубический ярдКубок (метрический)Кубок (Великобритания)Кубок (США)ДекалитрДецилитрДестистерДекастерДесертная ложка (Великобритания)Десертная ложка (США)драхмаКапляFemtoliterЖидкость Унция (Великобритания)Жидкость Унция (США)Галлон (Великобритания)Галлона (США)гигалитрГилл (Великобритания)Гилл (США)ГектолитрHin (библейский)хогсхедГомер (библейский)Сто кубический футкилолитрЛитрLog (библейский)мегалитрМикролитрМиллилитрMinim (Великобритания)Minim (США)нанолитрPetaliterпиколитрПинта (Великобритания)Пинта (США)Кварта (Великобритания)Quart (США)StereСтоловая ложка (метрическая)Столовая ложка (Великобритания)Столовая ложка (США)Таза (испанский)Чайная ложка (метрическая)Чайная ложка (Великобритания)Чайная ложка (США)тералитрTon РегистрацияТунОбъем Земли |
⎘ копия |
ⓘ Объем треугольной призмы [VT]
👎
Формула
сбросить
👍
Объем треугольной призмы Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Преобразование входов в базовый блок
Длина: 3 метр —> 3 метр Конверсия не требуется
Высота: 12 метр —> 12 метр Конверсия не требуется
Основание: 2 метр —> 2 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
36 Кубический метр —> Конверсия не требуется
<
10+ объем Калькуляторы
<
5 Объем треугольной призмы Калькуляторы
Объем треугольной призмы формула
Объем = (Длина*Высота*Основание)/2
VT = (L*h*b)/2
Что такое треугольная призма?
Треугольная призма — это многогранник (трехмерная форма), состоящий из двух треугольных оснований и трех прямоугольных сторон. Как и другие призмы, здесь два основания параллельны и конгруэнтны друг другу.
Всего у него 5 граней, 6 вершин и 9 ребер. Треугольная призма — это пентаэдр с девятью отдельными сетками.
Share
Copied!
Калькулятор треугольной призмы
Создано Ханной Памула, докторантом и Жасмин Дж. Мах
Отредактировано Богной Шик, Джеком Боуотером и Аденой Бенн
Последнее обновление: 05 октября 2022 г.
Содержание:
- Формулы треугольной призмы
- Объем треугольной призмы
- Площадь поверхности треугольной призмы
- Как найти объем треугольной призмы с помощью этого инструмента?
- Часто задаваемые вопросы
Если вы когда-нибудь задавались вопросом, как найти объем треугольной призмы, этот калькулятор треугольной призмы — то, что вам нужно. Он не только может рассчитать объем, но также может быть полезен, если вам нужно определить площадь поверхности треугольной призмы. Выберите вариант, который соответствует вашим потребностям, и экспериментируйте с инструментом! Если вам интересны формулы треугольной призмы за калькулятором, прокрутите вниз, чтобы узнать больше.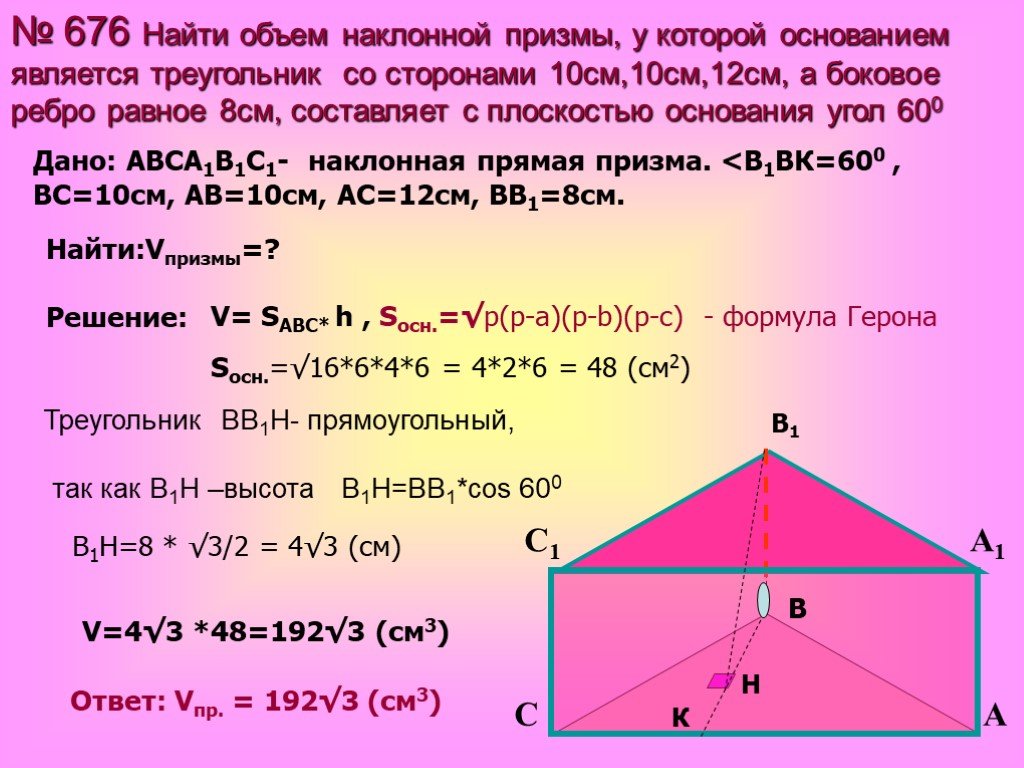
Что такое треугольная призма?
Треугольная призма представляет собой твердое тело, имеющее:
- два одинаковых треугольных основания
- три прямоугольные грани (прямая призма) или в форме параллелограмма (косая призма)
- одинаковое поперечное сечение по всей длине
Мы используем термин треугольная призма для описания правильной треугольной призмы, что является довольно распространенной практикой. Если вы ищете другой тип призмы, воспользуйтесь нашим калькулятором прямоугольных призм.
Формулы треугольной призмы
Обычно вам необходимо рассчитать объем треугольной призмы и площадь ее поверхности. Два самых основных уравнения:
-
объем = 0,5 * b * h * длина, гдеbдлина основания треугольника,hвысота треугольника,длинадлина призмы -
площадь = длина * (a + b + c) + (2 * base_area), гдеa, b, c— это стороны треугольника, аbase_area— это базовая площадь треугольника.
Но что, если у нас нет высоты и основания треугольника? А как найти площадь поверхности треугольной призмы без учета всех сторон треугольного основания? Ознакомьтесь с другими формулами треугольной призмы!
Объем треугольной призмы
В калькуляторе треугольной призмы вы можете легко узнать объем этого твердого тела. Общая формула: объем = длина * базовая_площадь ; единственный параметр, который вам всегда нужно указывать, — это длина призмы, и есть четыре способа рассчитать площадь основания — треугольника. Все они реализованы в нашем калькуляторе треугольной призмы. Разве это не потрясающе?
Конкретные формулы выглядят следующим образом:
-
Длина * Площадь основания треугольника Даны основание и высота треугольника
Это известная формула, упомянутая ранее:
объем = длина * 0,5 * ширина * высота -
Длина * Треугольная площадь основания с учетом трех сторон (SSS)
Если известны длины всех сторон, используйте
формулу Герона , чтобы найти площадь основания треугольника:объем = длина * 0,25 * √( (a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)) -
Длина * Площадь треугольного основания с учетом двух сторон и угла между ними (SAS)
Вы можете легко вычислить площадь треугольника с помощью тригонометрии:
объем = длина * 0,5 * a * b * sin(γ) -
Длина * Площадь основания треугольника с учетом двух углов и стороны между ними (ASA)
Вы можете вычислить это с помощью тригонометрии:
объем = = длина * a² * sin(β) * sin(γ) / (2 * sin(β + γ))
Площадь поверхности треугольной призмы
Если вы хотите рассчитать площадь поверхности твердого тела, наиболее известной формулой является формула для трех сторон треугольного основания:
-
площадь = длина * (a + b + c) + (2 * базовая_площадь) = длина * базовый_периметр + (2 * базовая_площадь)
Однако нам не всегда известны три стороны.
Что тогда?
-
Треугольное основание: по двум сторонам и углу между ними (SAS)
Используя закон косинусов, мы можем найти третью сторону треугольника:
площадь = длина * (a + b + √( b² + a² - (2 * b * a * cos(угол)))) + a * b * sin(угол) -
Треугольное основание: даны два угла и сторона между ними (ASA)
Используя закон синусов, мы можем найти две стороны треугольного основания:
площадь = (длина * (a + a * (sin(угол1) / sin(угол1+угол2)) + a * (sin(угол2) / sin(угол1+угол2)))) + a * ((a * грех(угол1)) / грех(угол1 + угол2)) * грех(угол2)
Единственный вариант, когда вы не можете вычислить объем треугольной призмы, это иметь заданное основание треугольника и его высоту (знаете почему? Задумайтесь об этом на минутку). Все остальные варианты можно рассчитать с помощью нашего калькулятора треугольной призмы.
Как найти объем треугольной призмы с помощью этого инструмента?
Проверим, каковы объем и площадь поверхности палатки в виде треугольной призмы:
- Выясним, какова длина треугольной призмы . Предположим, что оно равно 80 дюймам, введите это значение в первое поле калькулятора треугольной призмы.
- Выберите вариант с указанными параметрами . Например, даны три стороны нашей базы.
- Введите стороны основания . Наша палатка имеет a = 60 дюймов, b = 50 дюймов и c = 50 дюймов.
- Площадь поверхности и объем треугольной призмы появляются мгновенно . Это 96 000 кубических дюймов (55,56 кубических футов) и 15 200 дюймов² (105,56 футов²).
Предположим, что оно равно 80 дюймам, введите это значение в первое поле калькулятора треугольной призмы. FAQ
Как нарисовать треугольную призму?
Чтобы нарисовать треугольную призму:
- Нарисуйте основание призмы в виде треугольника.
- Нарисуйте верхнюю грань призмы в виде треугольника, параллельного основанию.
- Соедините соответствующие вершины обоих треугольников так, чтобы они не пересекались.
Сколько ребер у треугольной призмы?
Треугольная призма имеет 9 ребер, по три из которых образуют нижнюю и верхнюю грани.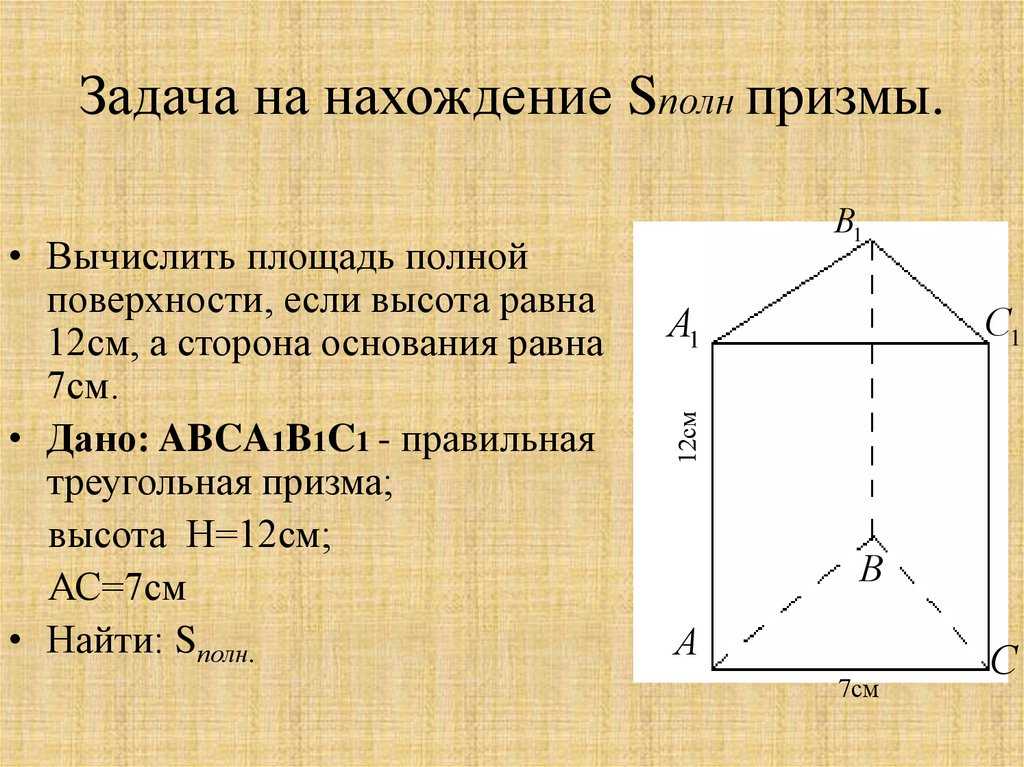
Остальные из них образуют боковые грани.
Сколько граней у треугольной призмы?
Треугольная призма имеет 5 граней, т. е. основание и верхнюю грань, а также 3 боковые грани.
Сколько вершин у треугольной призмы?
Треугольная призма имеет 6 вершин, т. е. по 3 на верхней и нижней треугольных гранях.
Ханна Памула, кандидат доктора философии и жасмин J MAH
Треугольный тип
Основание (B)
Высота (H)
Длина призмы (L)
Prism Том
Проверьте 21 Аналогичные геометрические раскаты 📦
. Площадь полушарияКубКуб Рассчитать: найти v, a, d… 18 больше
Объем треугольной призмы — Формула, определение, примеры
Объем треугольной призмы — это пространство, занимаемое ею со всех трех измерений. Призма представляет собой твердое тело, имеющее одинаковые основания, плоские прямоугольные боковые грани и одинаковое поперечное сечение по всей длине. Существуют различные типы призм, которые классифицируются и называются в соответствии с формой их основания.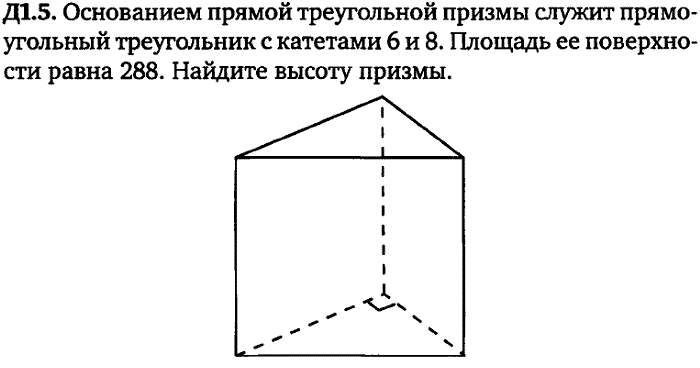
Треугольная призма имеет 2 одинаковых треугольных основания и 3 прямоугольные боковые грани.
| 1. | Каков объем треугольной призмы? |
| 2. | Объем треугольной призмы Формула |
| 3. | Как найти объем треугольной призмы? |
| 4. | Часто задаваемые вопросы по объему треугольной призмы |
Каков объем треугольной призмы?
Объем треугольной призмы можно рассчитать, взяв произведение площади треугольного основания и высоты призмы, также известной как длина призмы. Для этого давайте сначала разберемся, как выглядит треугольная призма.
Определение треугольной призмы
Треугольная призма представляет собой многогранник, состоящий из двух треугольных оснований и трех прямоугольных сторон. Или его можно рассматривать как пятигранник (всего у него 5 граней), в котором ребра и вершины оснований соединены друг с другом тремя прямоугольными сторонами.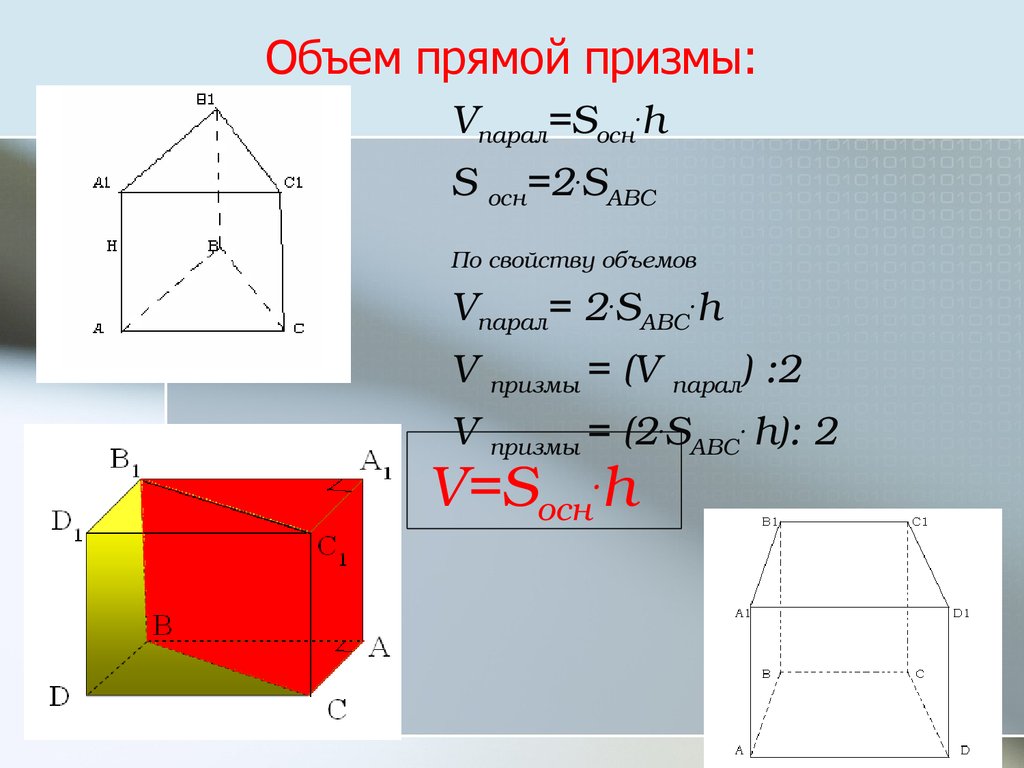
По определению, два треугольных основания параллельны и конгруэнтны друг другу. Он имеет:
- 2 основания (равные треугольники)
- 3 боковые грани (конгруэнтные прямоугольники)
- Общее количество граней — 5
- 9 ребер
- 6 углов или вершин
Длина треугольной призмы – это перпендикулярное расстояние между центрами двух оснований. Он представлен буквой «l» на рисунке ниже.
Обратите внимание на треугольную призму, показанную выше, где «b» — основание каждой стороны двух конгруэнтных треугольников, «h» — высота треугольника в основании, а «l» — длина призмы.
Объем треугольной призмы Формула
Объем треугольной призмы – это пространство внутри нее или занимаемое ею пространство. Он измеряется в кубических единицах, таких как см 3 , м 3 , 3 и т. д. Мы увидим формулы для расчета объемов различных типов треугольных призм. Объем любой призмы получается путем умножения площади ее основания на длину.
Объем призмы = площадь основания × длина призмы
Мы также будем использовать эту формулу для вычисления объема треугольной призмы. Мы знаем, что основание треугольной призмы — треугольник. Применяя приведенную выше формулу к треугольной призме, мы получаем:
Объем треугольной призмы = площадь треугольника с основанием × длина призмы
Здесь мы можем найти площадь треугольника с основанием на основе его типа и доступных Информация. В следующем списке показаны формулы для нахождения площади треугольника с основанием.
- Если треугольник в основании является равносторонним треугольником (в этом случае призма называется равносторонней треугольной призмой) с каждой стороной ‘a’, то его площадь = √3a 2 /4
- Если известны основание треугольника b и высота h, то его площадь = (1/2) bh
- Если треугольник в основании представляет собой прямоугольный треугольник (в этом случае призма называется прямоугольной треугольной призмой) с двумя катетами ‘b’ и ‘h’, то его площадь = (1/2) bh
- Если треугольник с основанием равнобедренный, стороны которого равны ‘a’, ‘a’ и ‘b’, то его площадь равна (b/4) × √(4a 2 — б 2 )
- Если треугольник с основанием представляет собой разносторонний треугольник, в котором даны все три стороны ‘a’, ‘b’ и ‘c’, то его площадь вычисляется по формуле √[s(s-a)(s-b)(s-c)]; где s = (а + b + с)/2. Обратите внимание, что вы можете применить эту формулу (которую также называют формулой Герона) для равнобедренного треугольника (или) равностороннего треугольника.
- Если известны две стороны базового треугольника ‘a’ и ‘b’ и угол между ними ‘θ’, то его площадь находится с помощью 1/2 ab sin θ
Обратите внимание, что вы можете применить эту формулу (которую также называют формулой Герона) для равнобедренного треугольника (или) равностороннего треугольника. Как найти объем треугольной призмы?
Объем треугольной призмы можно рассчитать с помощью следующих шагов и приведенного ниже примера. Перед этим убедитесь, что все измерения в одних и тех же единицах.
- Шаг 1: Определите тип базового треугольника и найдите его площадь, используя подходящую формулу (как описано в предыдущем разделе).
- Шаг 2: Определите длину призмы (Обратите внимание, что эта длина призмы также известна как высота призмы, и ее не следует путать с высотой треугольника основания).
- Шаг 3: Умножьте площадь основания (из шага 1) и длину призмы, чтобы найти объем.
Пример: Вычислите объем треугольной призмы длиной 15 дюймов, основанием которой является равносторонний треугольник со стороной 6 дюймов.
Решение: Объем треугольной призмы можно рассчитать, выполнив следующие действия.
- Шаг 1: Треугольник с основанием является равносторонним треугольником со стороной a = 6. Таким образом, его площадь находится по формуле √3a 2 /4 = √3(6) 2 /4 = 9√3 квадратных дюйма.
- Шаг 2: Длина призмы 15 дюймов.
- Шаг 3: Объем заданной треугольной призмы = площадь основания × длина = 9√3 × 15 = 135√3 кубических дюйма.
Советы по объему треугольной призмы
- Длина треугольной призмы также известна как высота призмы.
- Эту высоту призмы не следует путать с высотой основания треугольника.
☛ Статьи по теме
- Объем 3D-фигур
- Объем куба
- Объем цилиндра
- Объем кубоида
- Объем сферы
- Объем прямоугольной призмы
Примеры объема треугольной призмы
-
Пример 1: Определите объем треугольной призмы, в которой основание равно 7 дюймов, высота 5 дюймов, а длина призмы 10 дюймов.
Решение:
Основание треугольника (b) = 7 дюймов, высота основания треугольника (h) = 5 дюймов
Итак, площадь основания = (1/2)(bh) = (1/2) × (7 × 5) = 35/2 в 2 .
Длина призмы L = 10 дюймов.
Используя формулу объема треугольной призмы,
Объем данной треугольной призмы = площадь основания × длина призмы = (35/2) × (10) = 175 в 3 .
-
Пример 2: Найдите объем следующей прямоугольной призмы.
Решение:
Основание треугольника (b) = 14 футов, а его высота (h) = 8 футов.
Таким образом, площадь основания = (1/2) × (bh) = (1/2) × (14 × 8) = 56 квадратных футов.
Длина призмы L = 10 футов.
Используя формулу объема треугольной призмы,
Объем данной треугольной призмы = площадь основания × длина призмы = 56 × 10 = 560 футов 3 .
-
Пример 3: Укажите истинное или ложное значение.
а.) Треугольная призма – это многогранник, состоящий из двух треугольных оснований и трех прямоугольных сторон.
b.) Объем треугольной призмы измеряется в квадратных единицах, таких как см 2 , м 2 , 2 и так далее.
Решение:
а.) Верно, что треугольная призма представляет собой многогранник, состоящий из двух треугольных оснований и трех прямоугольных сторон.
б.) Неверно, объем треугольной призмы измеряется в кубических единицах, таких как см 3 , м 3 , в 3 и так далее.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по объему треугольной призмы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по объему треугольной призмы
Каков объем треугольной призмы?
Объем треугольной призмы — это пространство внутри нее.
Он рассчитывается путем умножения площади треугольного основания на высоту призмы, также известную как длина призмы. Объем треугольной призмы выражается в кубических единицах, таких как см 3 , м 3 , 3 и т. д.
Какая формула для нахождения объема треугольной призмы?
Формула для нахождения объема треугольной призмы: Объем = площадь основания × длина, где
- Площадь основания = площадь основания (треугольника)
- Длина = длина треугольной призмы (также известная как высота призмы)
Как найти высоту треугольной призмы по объему?
Высота треугольной призмы также известна как длина призмы. Его можно вычислить, если известны площадь основания и объем призмы. Формула объема треугольной призмы = площадь основания × длина призмы. Отсюда высота треугольной призмы получается делением ее объема на площадь основания.
Как найти объем треугольной призмы с прямым углом?
Если основание треугольной призмы представляет собой прямоугольный треугольник с основанием «b» и высотой «h», а длина призмы равна «L», то площадь ее основания = (1/2) bh.
Мы знаем что объем призмы = площадь основания × длина призмы, поэтому объем призмы в этом случае рассчитывается по той же формуле Объем треугольной призмы = (1/2) bh × L.
По какой формуле вычислить объем равносторонней треугольной призмы?
Рассмотрим треугольную призму, длина которой равна «L», а основание — равносторонний треугольник со стороной «а». Тогда его базовая площадь равна √3a 2 /4. Мы знаем, что объем призмы = площадь основания × длина призмы, следовательно, объем призмы в данном случае находится по формуле (√3a 2 × L)/4
Как найти объем треугольной призмы с заданным углом?
Рассмотрим треугольную призму, длина которой равна «L», а «а» и «b» — это две стороны ее основания с прилежащим к ней углом θ. Тогда его базовая площадь равна (1/2) ab × sin θ. Мы знаем, что объем призмы равен площади основания × длине призмы, поэтому объем призмы в данном случае находится по формуле (1/2) ab sin θ × L.
Как площадь треугольника связана с объемом треугольной призмы?
Площадь треугольника используется для нахождения объема треугольной призмы, поскольку основание треугольной призмы представляет собой треугольник, а формула, используемая для нахождения объема треугольной призмы, такова: Объем = площадь основания × длина призма, где площадь основания равна площади треугольника.
Объём — это аддитивная функция от множества (мера), характеризующая вместимость области пространства, которую оно занимает. Изначально возникло и применялось без строгого определения в отношении тел трёхмерного евклидова пространства. Первые точные определения были даны Пеано (1887) и Жорданом (1892). Впоследствии понятие было обобщено Лебегом на более широкий класс множеств.
Для определения объёма существует несколько существенно различных подходов, которые дополняют друг друга и согласованы по конечному результату на «хороших множествах». Обычно под понятием объёма понимается мера Жордана, но иногда мера Лебега. Для римановых многообразий понятие объёма вводится аналогично понятию площади поверхности.
Все формулы объема геометрических тел
Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a 3
где:
V – объем куба,
a – длина грани куба.
Объем призмы
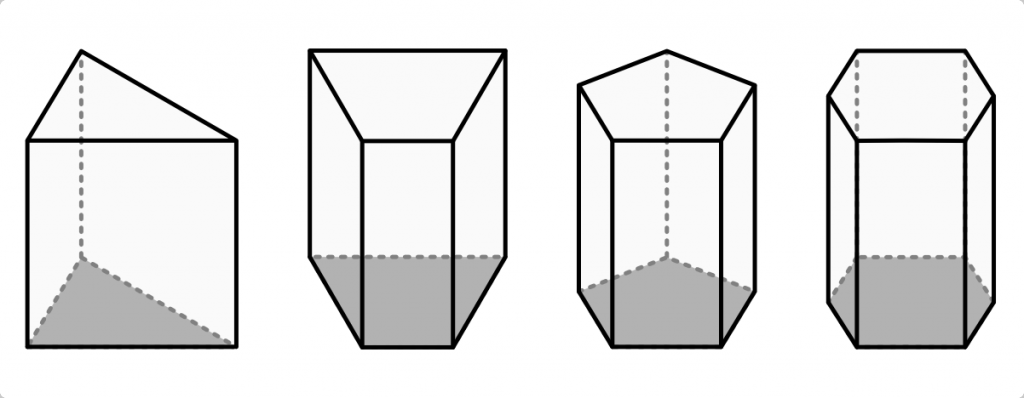
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
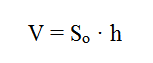
где:
V- объем призмы,
So – площадь основания призмы,
h – высота призмы.
Объем параллелепипеда
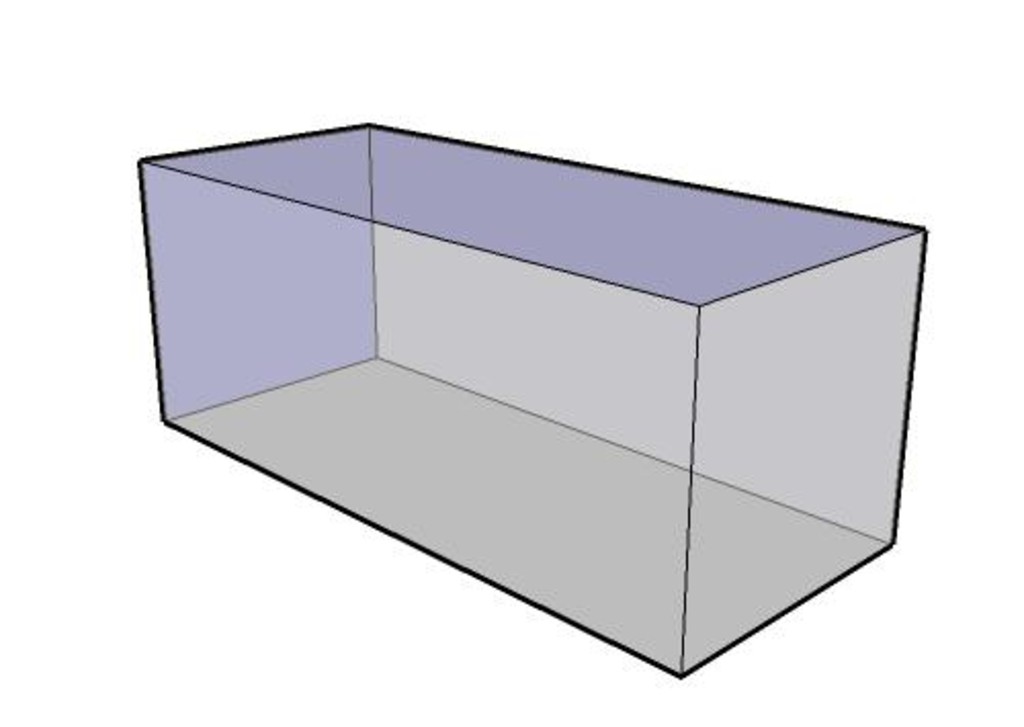
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
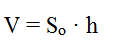
где:
V- объем параллелепипеда,
So – площадь основания,
h – длина высоты.
Объем пирамиды
Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).
Формула объема пирамиды:
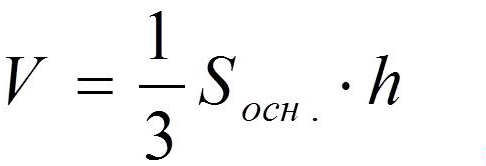
где:
V – объем пирамиды,
So – площадь основания пирамиды,
h – длина высоты пирамиды.
Объем усеченной пирамиды
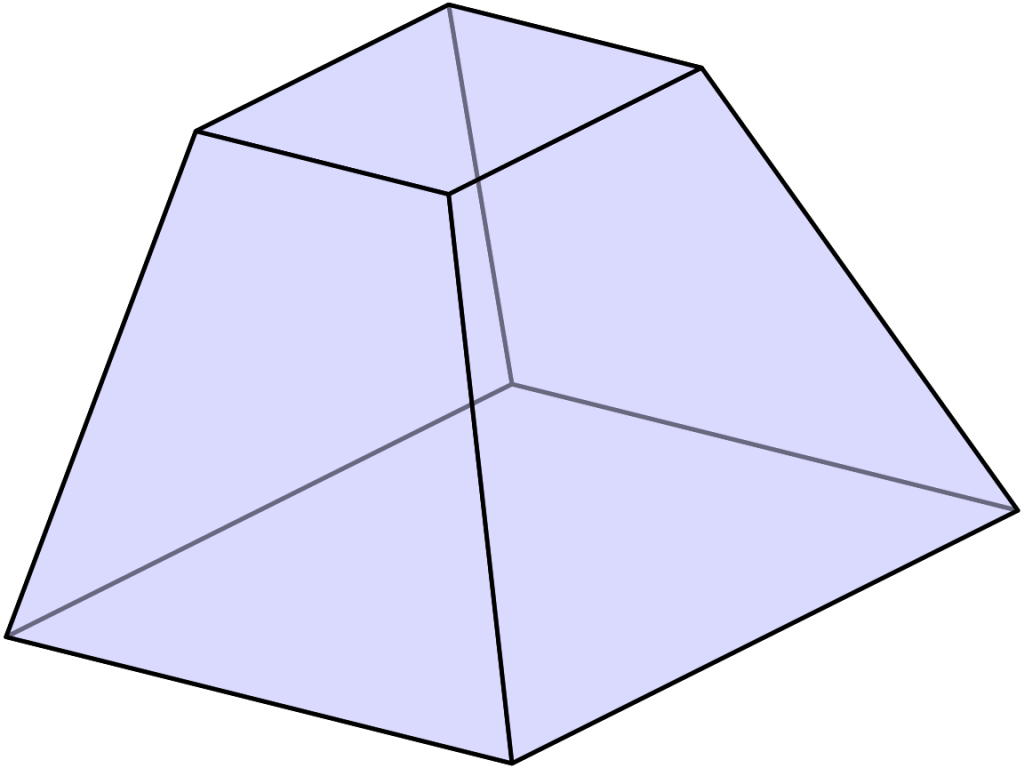
Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1(abcde), нижнего основания усеченной пирамиды S2 (ABCDE) и средней пропорциональной между ними.
Формула объема усеченной пирамиды:
Где:
S1 – площадь верхнего основания усеченной пирамиды,
S2 – площадь нижнего основания усеченной пирамиды,
h – высота усеченной пирамиды.
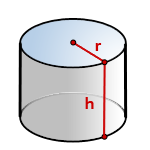
Объем цилиндра
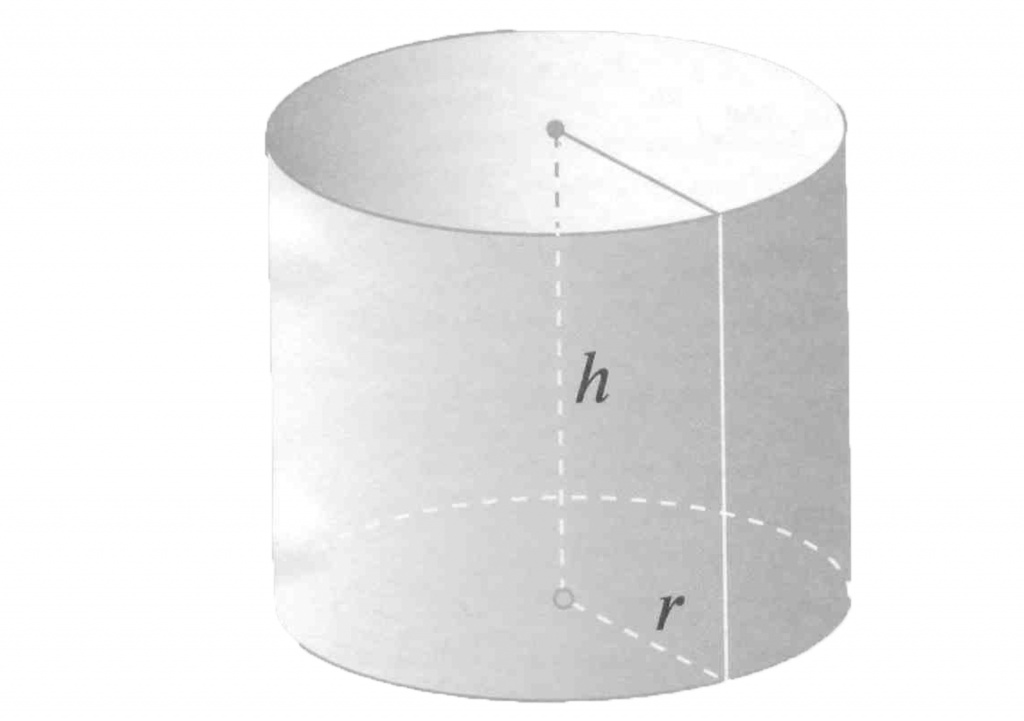
Объем цилиндра равен произведению площади его основания на высоту.
Формула объема цилиндра:
V= π R2 h
V= Sоh
Где:
V – объем цилиндра,
So – площадь основания цилиндра,
R – радиус цилиндра,
h – высота цилиндра,
π = 3.141592
Объем правильной треугольной пирамиды
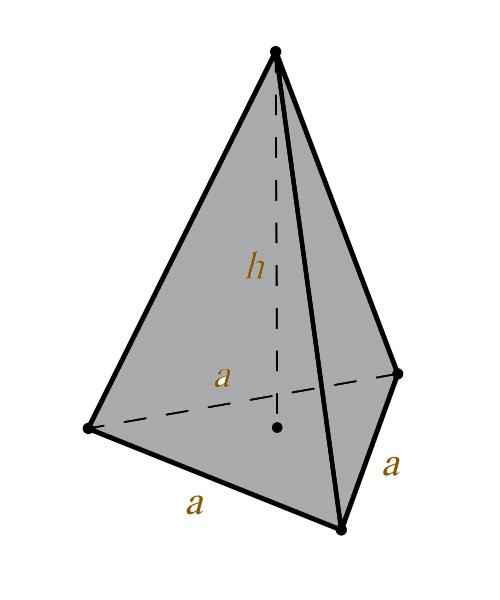
Объем правильной треугольной пирамиды равен одной трети произведения площади правильного треугольника, являющегося основанием S (ABC) на высоту h (OS).
Формула объема правильной треугольной пирамиды:
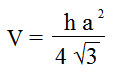
Где:
V – объем пирамиды;
h – высота пирамиды;
a – сторона основания пирамиды.
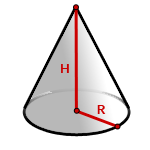
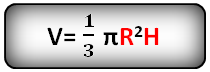
Объем конуса
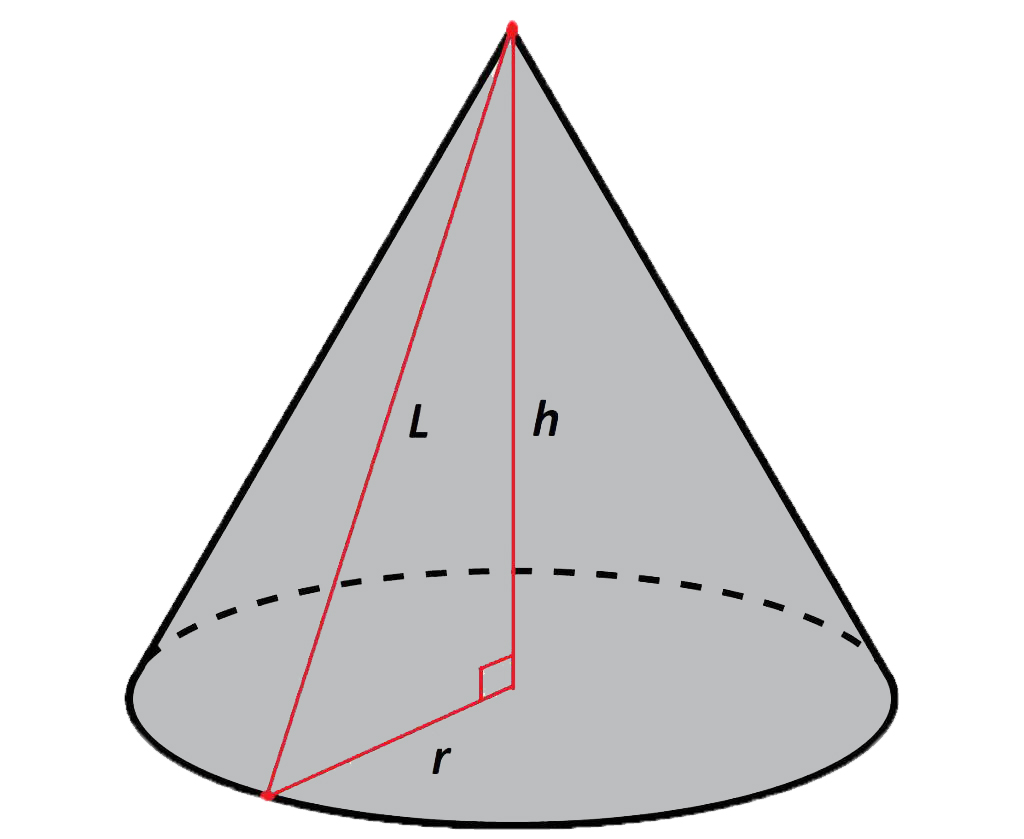
Объем круглого конуса равен трети произведения площади основания S на высоту H.
Формула объема конуса:
Где:
V – объем конуса;
R – радиус основания;
H – высота конуса;
I – длина образующей;
S – площадь боковой поверхности конуса.
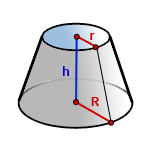
Объем усеченного конуса
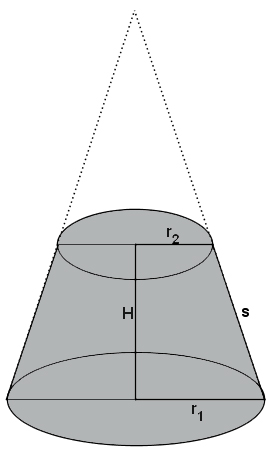
Объем усеченного конуса равен разности объемов двух полных конусов.
Формула объема усеченного конуса:
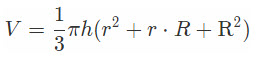
Где:
V – объем усеченного конуса;
H – высота усеченного конуса;
R и R2 – радиусы нижнего и верхнего оснований.
Объем тетраэдра
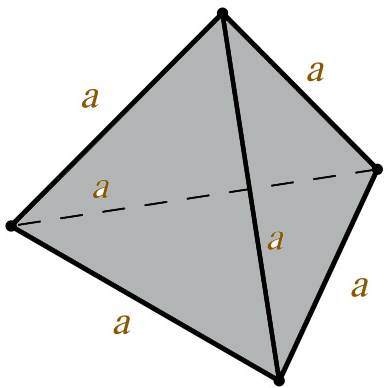
Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.
Формула тетраэдра:
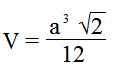
Где:
V – объем тетраэдра;
a – ребро тетраэдра.
Объем шара
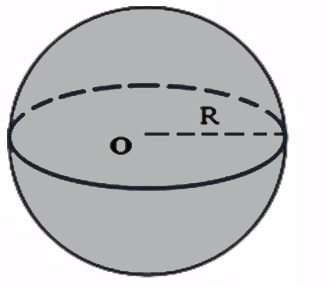
Объем шара равен четырем третьим от его радиуса в кубе перемноженного на число пи.
Формула объема шара:
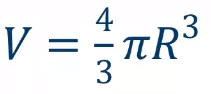
Где:
V – объем шара;
R – радиус шара;
S – площадь сферы.
Объем шарового сегмента и сектора
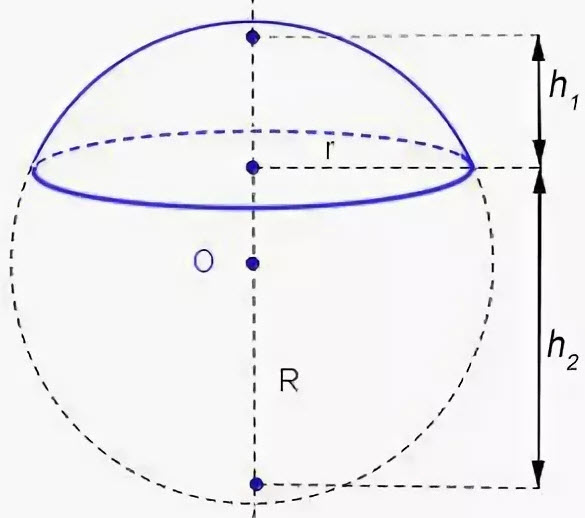
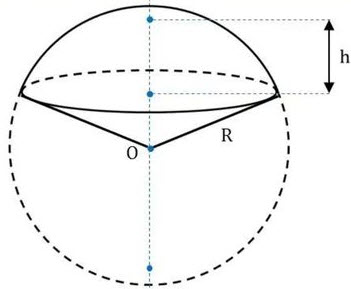
Шаровый сегмент – это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.
Формула объема шарового сегмента:
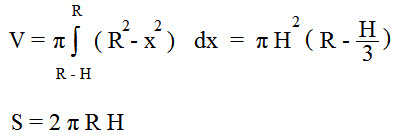
Где:
R – радиус шара
H – высота сегмента
π ≈ 3,14
Формула объема шарового сектора:
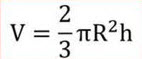
Где:
h – высота сегмента
R – радиус шара
π ≈ 3,14
Объем прямоугольного параллелепипеда
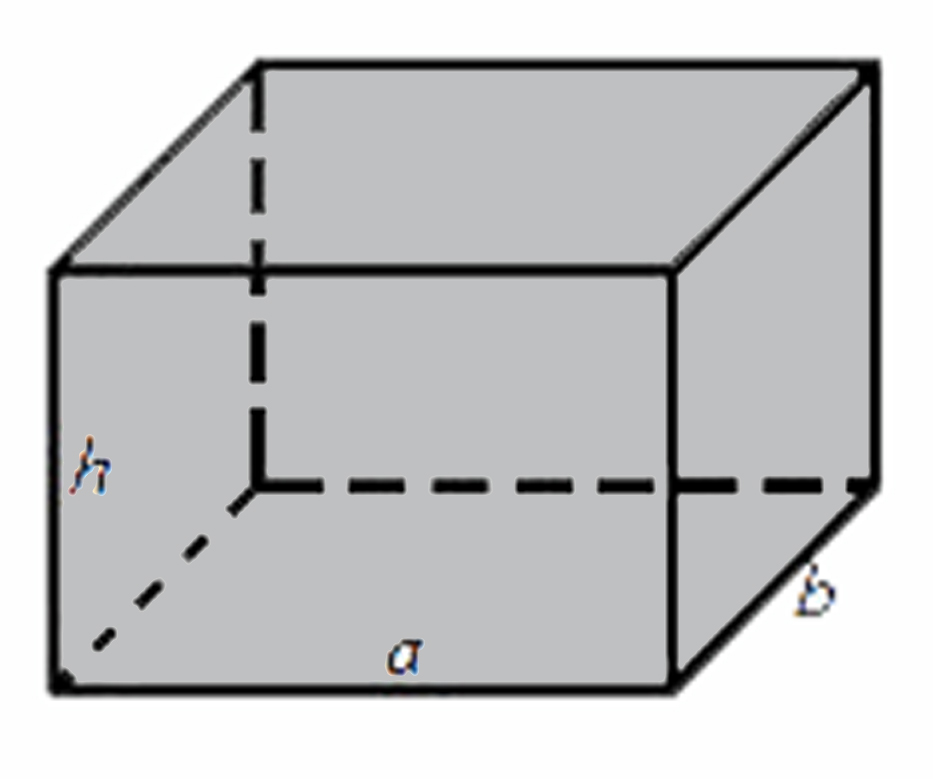
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
Где:
V – объем прямоугольного параллелепипеда,
a – длина,
b – ширина,
h – высота.
