Как найти объем правильной квадратной призмы

A square prism is a three-dimensional-shaped geometric structure that has two congruent square bases that are connected by four rectangular faces. A prism having a square base is defined as a square prism. All cubes fulfill all the properties of a square prism, so all cubes are square prisms, but not all square prisms are cubes. A square prism has a total of six faces (two square bases and four rectangular faces), twelve edges, and eight vertices. The lateral faces (or) sides faces are rectangles, and the two bases are squares, the area of the prism is the total area of all its faces. Depending upon the alignment of the square bases, a square prism is classified into two types, a right square prism, and an oblique square prism. Right square prisms have lateral faces that are perpendicular to their square bases, whereas oblique square prisms have lateral faces that aren’t perpendicular to the square bases.

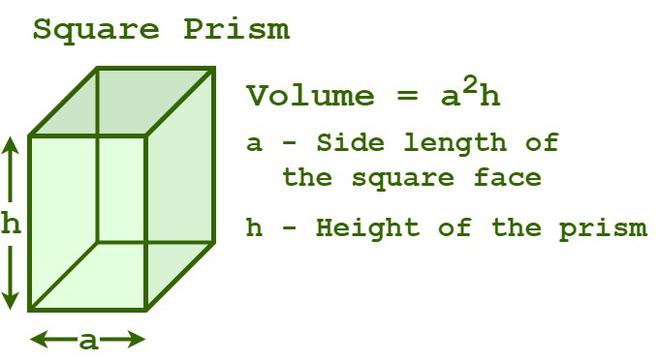
Volume of Square Prism

The volume of a square prism is the total amount of space that is enclosed by the prism. The volume or capacity is in terms of cubic units and is equal to the product of the base area and the height.

Formula for calculating the volume of any prism is given as follows:

Volume of a prism (V) = Base area × Height of the prism

Volume of Square Prism Formula

The formula for finding the volume of a square prism is base multiplied by area.

Now, the two congruent bases of the prism are squares. 

Hence, the base area = (edge)² = a² square units

Now, substitute the values in the above formula, we get

Volume of a square prism = a²h cubic units

Where “a” is the side of the square base and, “h” is the height of the square prism.

How To Calculate the Volume of Square Prism?

Steps to Calculate the Volume of Square Prism are explained below:

Step 1: 

Write the given dimensions of the square prism. Now s = side of square prism, s² = area of the base, and h = height of square prism.
Make sure that the units of s and h should be the same.

Step 2: 

Put these respective values in the volume of square prism formula s²h.

Step 3: 

The value obtained is the volume of the square prism. Write the unit of the volume of the square prism is in terms of units³.

Consider the following example:

Example: Find the volume of a square prism if the edge of the base is 9 and its height is 11.

Solution:

Given data,

edge of base = 9

height of a square prism (h) = 11

We have,

The Volume of a square prism = Base area × height of the prism

By substituting the values in the formula, we get

= 9² × 11 = 891 cu. units

Therefore, the volume of a square prism is 891 cu. units.

Solved Examples based on the Volume of a Square Prism

Example 1: Calculate the volume of a square prism whose side is 10 inches and whose height is 15 inches.

Solution:

Given data,

The length of the side of a square prism (a) = 10 inches

The height of a square prism (h) = 15 inches

We have,

The Volume of a square prism = a²h cubic units

= (10)² × 15

= 100 × 15 = 1500 cu. in

Thus, the volume of the given prism is 1500 cu. in.

Example 2: Find the volume of a square prism if the length of the side of the square face of a square prism is 12 cm and its height is 17 cm.

Solution:

Given data,

The length of the side of a square prism (a) = 12 cm

The height of a square prism (h) = 17 cm

We have,

The Volume of a square prism = a²h cubic units

= (12)² × 17

= 144 × 17 = 2448 cu. cm

Therefore, the volume of a square prism is 2448 cu. cm.

Example 3: Determine the volume of a square prism whose length of the side of the square face is 8 units and whose height is 10 units.

Solution:

Given data,

The length of the side of a square prism (a) = 8 units

The height of a square prism (h) = 10 units

We have,

The Volume of a square prism = a²h cubic units

Now, substitute the values of a and h in the formula.

= (8)² × 10

= 64 × 10 = 640 cubic units

Thus, the volume of the given prism is 640 cubic units.

Example 4: Find the length of the edge of the square prism if the volume of the square prism is 1,694 cu. cm and the height is 14 cm. 

Solution:

Given data,

The height of a square prism (h) = 14 cm

The volume of a square prism = 1694 cu. cm

We have,

The Volume of a square prism = a²h cubic units

By substituting the values in the formula, we get

⇒ 1694 = (a²) × (14)

⇒  a² = 1694 ÷ 14 = 121

⇒ a = √121 = 11 cm

Thus, the length of the edge of the square prism is 11 cm.

FAQs on Volume of a Square Prism

Question 1: What is the formula for finding the volume of a square prism?

Answer:

Formula for calculating the volume of prism is given by V = (base area) × (height of the prism). A square prism is a prism whose base is in the shape of a square. 

Volume of a square prism = a²h cubic units.

 Here, “a” is the length of the side of the square face and “h” is the height of the square prism.

Question 2: What will happen to the volume of a square prism if the height of the square prism is doubled?

Answer:

We know that the formula for calculating the volume of any prism is (base area) × (height of the prism). We can clearly say that the volume of the prism is directly proportional to its height. So, as the height of the square prism is doubled, its volume will also be doubled.

Question 3: What happens to the volume of a square prism if the length of the square face is reduced to half?

Answer:

The formula for calculating the volume of a square prism.

V = a²h cubic units. 

Here, “a” is the edge length of the square face, and “h” is the height of the square prism. Thus, the volume of the prism is directly proportional to the square of the length of edge of square face.

V’ = (a/2)²h = (a²h)/4 = V/4

So, the new volume of the square prism is one-fourth of its old volume.

Question 4: How can we find the height of a square prism if the volume of the square prism and the length of the edge of the base are given?

Answer:

Follow the given steps below to find the height of a square prism if the volume of the square prism and the length of the edge of the base are given:

Step 1: First, note down the given dimensions of the prism, i.e., the volume (V), and length of the edge (a).

Step 2: Now, substitute the given values in the formula V = a² h.

Step 3: Finally, solve the equation to get the height (h) of the square prism.

Last Updated :
22 Aug, 2022

Like Article

Save Article

В школьной программе по курсу стереометрии изучение объёмных фигур обычно начинается с простого геометрического тела — многогранника призмы. Роль её оснований выполняют 2 равных многоугольника, лежащих в параллельных плоскостях. Частным случаем является правильная четырёхугольная призма. Её основами являются 2 одинаковых правильных четырёхугольника, к которым перпендикулярны боковые стороны, имеющие форму параллелограммов (или прямоугольников, если призма не наклонная).

Как выглядит призма

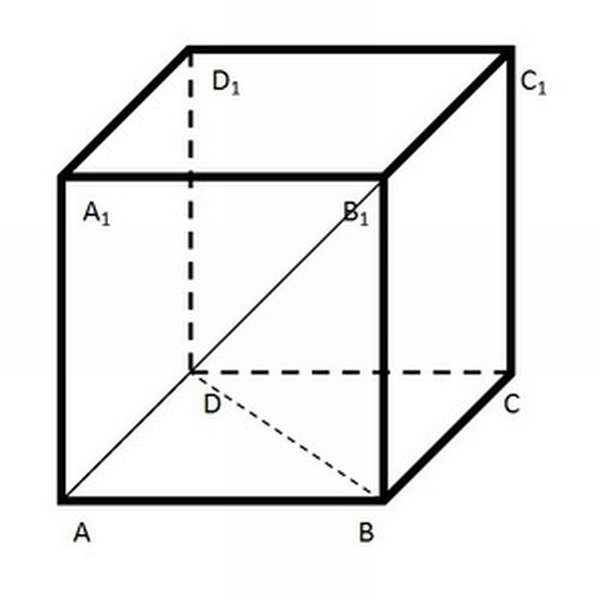
Правильной четырёхугольной призмой называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Иное название для этой геометрической фигуры — прямой параллелепипед.

Рисунок, на котором изображена четырёхугольная призма, показан ниже.

На картинке также можно увидеть важнейшие элементы, из которых состоит геометрическое тело. К ним принято относить:

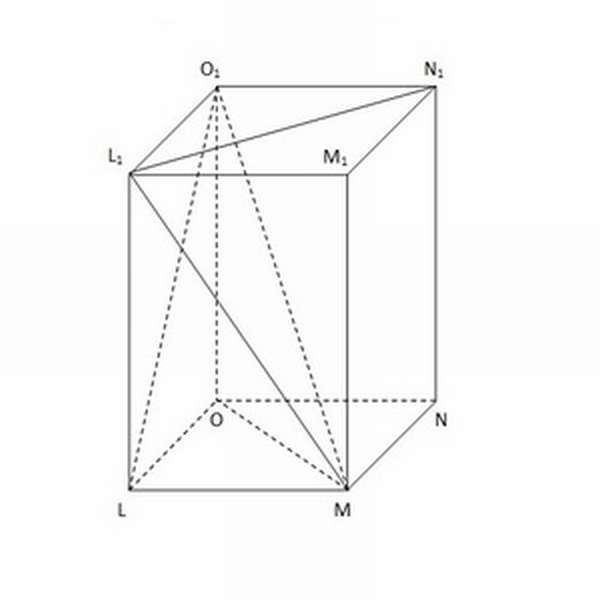1. Основы призмы — квадраты LMNO и L₁M₁N₁O₁.
2. Боковые грани — прямоугольники MM₁L₁L, LL₁O₁O, NN₁O₁O и MM₁N₁N, расположенные под прямым углом к основаниям.
3. Боковые рёбра — отрезки, расположенные на стыке между двумя боковыми гранями: M₁M, N₁N, O₁O и L₁L. Также выполняют роль высоты (поскольку лежат в параллельной основаниям плоскости). В призме боковые рёбра всегда равны между собой — это одно из важнейших свойств этого геометрического тела.
4. Диагонали, которые, в свою очередь, подразделяются ещё на 3 категории. К ним относится 4 диагонали основания (MO, N₁L₁), 8 диагоналей боковых граней (ML₁, O₁L) и 4 диагонали призмы, начала и концы которых являются вершинами 2 разных оснований и боковых сторон (MO₁, N₁L).

Иногда в задачах по геометрии можно встретить понятие сечения. Определение будет звучать так: сечение — это все точки объёмного тела, принадлежащие секущей плоскости. Сечение бывает перпендикулярным (пересекает рёбра фигуры под углом 90 градусов). Для прямоугольной призмы также рассматривается диагональное сечение (максимальное количество сечений, которых можно построить — 2), проходящее через 2 ребра и диагонали основания.

Если же сечение нарисовано так, что секущая плоскость не параллельна ни основам, ни боковым граням, в результате получается усечённая призма.

Для нахождения приведённых призматических элементов используются различные отношения и формулы. Часть из них известна из курса планиметрии (например, для нахождения площади основания призмы достаточно вспомнить формулу площади квадрата).

Площадь поверхности и объём

Чтобы определить объём призмы по формуле, необходимо знать площадь её основания и высоту:

V = Sосн·h

Так как основанием правильной четырёхгранной призмы является квадрат со стороной a, можно записать формулу в более подробном виде:

V = a²·h

Если речь идёт о кубе — правильной призме с равной длиной, шириной и высотой, объём вычисляется так:

V = a³

Чтобы понять, как найти площадь боковой поверхности призмы, необходимо представить себе её развёртку.

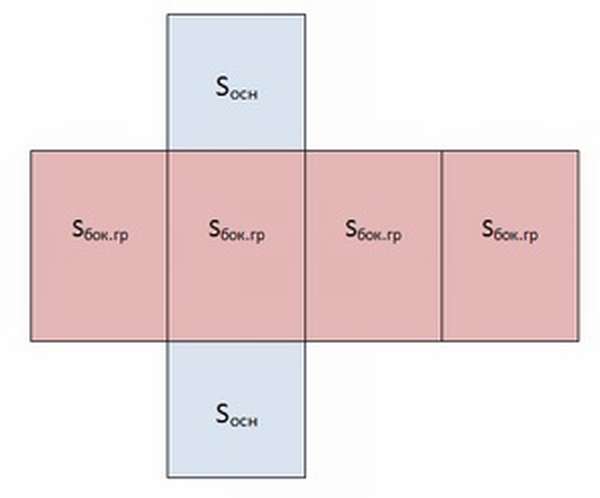
Из чертежа видно, что боковая поверхность составлена из 4 равных прямоугольников. Её площадь вычисляется как произведение периметра основания на высоту фигуры:

Sбок = Pосн·h

С учётом того, что периметр квадрата равен P = 4a, формула принимает вид:

Sбок = 4a·h

Для куба:

Sбок = 4a²

Для вычисления площади полной поверхности призмы нужно к боковой площади прибавить 2 площади оснований:

Sполн = Sбок + 2Sосн

Применительно к четырёхугольной правильной призме формула имеет вид:

Sполн = 4a·h + 2a²

Для площади поверхности куба:

Sполн = 6a²

Зная объём или площадь поверхности, можно вычислить отдельные элементы геометрического тела.

Нахождение элементов призмы

Часто встречаются задачи, в которых дан объём или известна величина боковой площади поверхности, где необходимо определить длину стороны основания или высоту. В таких случаях формулы можно вывести:

• длина стороны основания: a = Sбок / 4h = √(V / h),
• длина высоты или бокового ребра: h = Sбок / 4a = V / a²,
• площадь основания: Sосн = V / h,
• площадь боковой грани: Sбок. гр = Sбок / 4.

Чтобы определить, какую площадь имеет диагональное сечение, необходимо знать длину диагонали и высоту фигуры. Для квадрата d = a√2. Из этого следует:

Sдиаг = ah√2

Для вычисления диагонали призмы используется формула:

dприз = √(2a² + h²)

Чтобы понять, как применять приведённые соотношения, можно попрактиковаться и решить несколько несложных заданий.

Примеры задач с решениями

Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.

Задание 1.

В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?

Решение.

Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:

V₁ = ha² = 10a²

Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:

V₂ = h (2a)² = 4ha²

Поскольку V₁ = V₂, можно приравнять выражения:

10a² = 4ha²

После сокращения обеих частей уравнения на a² получается:

10 = 4h

В результате новый уровень песка составит h = 10 / 4 = 2,5 см.

Задание 2.

ABCDA₁B₁C₁D₁ правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.

Решение.

Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.

Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.

Длина любого ребра определяется через известную диагональ:

a = d / √2 = 6√2 / √2 = 6

Площадь полной поверхности находится по формуле для куба:

Sполн = 6a² = 6·6² = 216

Задание 3.

В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?

Решение.

Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.

Длина комнаты составляет a = √9 = 3 м.

Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².

Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.

Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.

Как найти площадь куба

Проститутки Ростов на Дону rostovchanotki.ru

Определение призмы

Призма — многогранное тело, основаниями которого являются два равных многоугольника, лежащие в параллельных плоскостях. Остальными гранями являются параллелограммы.

Такие параллелограммы в призме называются боковыми.

Онлайн-калькулятор объема призмы

Призмы разделяют на некоторые типы:

1. Треугольная призма — у нее основания — треугольники;
2. Четырехугольная призма — у нее основания — четырехугольники;
3. Пентапризма — пятиугольная призма.

Деление, в общем, продолжается до бесконечности.

Виды призм

Прямая — у такой призмы боковые грани образуют с основаниями прямой угол.
Правильная — ее основанием является какой-либо правильный многоугольник.
Усеченной называется призма, у которой основания не параллельны друг другу.

Формула объема призмы

Объем прямой призмы находится так же, как и объем других многогранников — путем умножения площади основания на высоту.

Объем призмы

V=Sосн⋅hV=S_{text{осн}}cdot h

SоснS_{text{осн}} — площадь основания призмы;
hh — высота призмы.

Разберем задачу на нахождение объема прямой призмы.

Задача

Найти объем призмы, если ее основанием является равнобедренный треугольник с равными сторонами по 5 см5text{ см} и основанием в 6 см6text{ см}. Высота призмы равна 10 см10text{ см}.

Решение

a=5a=5
b=6b=6
h=10h=10

Вычисляем площадь основания. Нужно провести высоту в данном равнобедренном треугольнике. Тогда, по теореме Пифагора, получаем:

a2=l2+(b2)2a^2=l^2+Big(frac{b}{2}Big)^2,

где ll — высота равнобедренного треугольника.

Отсюда:

l2=a2−(b2)2l^2=a^2-Big(frac{b}{2}Big)^2

l=a2−(b2)2l=sqrt{a^2-Big(frac{b}{2}Big)^2}

l=25−9l=sqrt{25-9}

l=4l=4

Площадь равнобедренного треугольника SS это половина от произведения его основания на высоту:

S=12⋅b⋅l=12⋅6⋅4=12S=frac{1}{2}cdot bcdot l=frac{1}{2}cdot 6cdot 4=12

В нашем случае этот треугольник является основанием призмы, поэтому:

S=SоснS=S_{text{осн}}

Тогда объем призмы найдется по формуле:

V=Sосн⋅h=12⋅10=120 см3V=S_{text{осн}}cdot h=12cdot 10=120text{ см}^3

Ответ

120 см3.120text{ см}^3.

На нашем сайте вы можете оформить решение задач на заказ по самым низким ценам!

Тест по теме «Объем призмы»

В данной публикации мы рассмотрим, как можно найти объем призмы и разберем примеры решения задач для закрепления материала.

• Формула вычисления объема призмы

• Примеры задач

Формула вычисления объема призмы

Объем призмы равняется произведению площади ее основания на высоту.

V = S_осн ⋅ h

• S_осн – площадь основания, т.е. в нашем случае – четырехугольника ABCD или EFGH (равны между собой);
• h – высота призмы.

Приведенная выше формула подходит для следующих видов призм: 

• прямой – боковые ребра перпендикулярны основанию;
• правильной – прямая призма, основанием которой является правильный многоугольник;
• наклонной – боковые ребра расположены под углом по отношению к основанию.

Примеры задач

Задание 1
Найдите объем призмы, если известно, что площадь ее основания равна 14 см², а высота – 6 см.

Решение:
Подставляем в формулу известные нам значения и получаем:
V = 14 см² ⋅ 6 см = 84 см³.

Задание 2
Объем призмы равняется 106 см³. Найдите ее высоту, если известно, что площадь основания составляет 10 см².

Решение:
Из формулы расчета объема следует, что высота равняется объему, разделенному на площадь основания:
h = V / S_осн = 106 см³ / 10 см² = 10,6 см.

Что такое призма

Призма — это трехмерное геометрическое тело с двумя равными основаниями и плоскими гранями. Название зависит от фигуры, которая лежит в ее основании. Например, если это треугольник, призму называют «треугольной».

Эта объемная фигура может быть нескольких видов:

1. Прямая. То есть с боковыми ребрами, перпендикулярными основанию.
2. Правильная. В основании лежит правильный многоугольник.
3. Наклонная. Ее ребра расположены под углом к основанию.

Формулы вычисления объема правильной призмы

Правильные призмы могут быть разных видов, в зависимости от многоугольника, который лежит в их основании. Формула вычисления объема во всех случаях выглядит одинаково:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(V=Scdot h)

Разница лишь в том, каким образом находится площадь S для каждой из фигур.

Треугольная

Чтобы вычислить объем призмы, в основании которой лежит правильный треугольник, используем формулу:

(V=frac{sqrt3}4cdot a^2cdot h)

Где (frac{sqrt3}4cdot a^2=S) — площадь правильного треугольника в основании, a — сторона треугольника, h — высота всей фигуры.

Четырехугольная  

Для фигуры, в основании которой лежит квадрат, используем следующую формулу для вычисления объема:

(V=a^2cdot h)

Где a — сторона квадрата.

Пятиугольная

В этом случае объем будет вычисляться по формуле:

(V=frac52cdot acdotsqrt{left(frac a{2sinleft({displaystylefracpi5}right)}right)^2-frac{a^2}4}cdot h\)

Шестиугольная

Для призмы с правильным шестиугольником в основании формула объема выглядит так:

(x = V=frac{3sqrt3}2cdot a^2cdot h\)

Объем наклонной и прямой

Он находится через произведение площади основания на высоту:

(V=Scdot h\)

Таким образом, формула вычисления объема совпадает с предыдущими вариантами и зависит лишь от фигуры в основании.

С прямой призмой все то же самое. Сначала нужно вычислить площадь ее основания, а потом умножить на высоту.

Примеры задач

Решение:

Так как уже дана площадь основания, нам не важно какая фигура лежит в основании. Подставляем известные значения в формулу:

(V=Scdot h=12cdot5=60 ) (см^3)

Ответ: V=60 (см^3.)

Решение:

Так как сначала для вычисления объема нам нужно определить площадь четырехугольника, будем использовать уравнение: (V=acdot bcdot h)

Подставляем значения: (V=6cdot3cdot10=180) (см^3)

Ответ: V=180 (см^3.)