Как найти объем призмы правильной четырехугольной пирамиды

Найдите объём правильной четырёхугольной пирамиды

Формулировка задачи: Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна K, а боковое ребро равно N.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

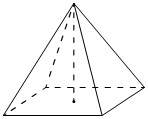
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 8, а боковое ребро равно √41.

Объем любой пирамиды равен:

В основании правильной четырехугольной пирамиды лежит квадрат со стороной 8. Поэтому площадь основания равна:

Теперь нужно вычислить высоту пирамиды, используя сторону основания и боковое ребро. Для этого проведем диагональ в основании правильной четырёхугольной пирамиды. Диагональ квадрата в основании равна:

Получим прямоугольный треугольник, катетами которого являются половина диагонали и высота пирамиды, а гипотенузой – боковое ребро пирамиды. Поэтому высоту пирамиды можно вычислить по теореме Пифагора:

h = √ 41 – (4√ 2 ) 2 = √ 41 – 32 = 3

Осталось найти объем пирамиды, подставив все полученные данные:

В общем виде решение данной задачи по стереометрии выглядит следующим образом:

V = 1/3 ⋅ K 2 ⋅ √ N 2 – (K/2 ⋅ √ 2 ) 2

где K – сторона основания, N – боковое ребро.

Остается лишь подставить конкретные значения и подсчитать результат.

Поделитесь статьей с одноклассниками «Найдите объём правильной четырёхугольной пирамиды – как решать».

Источник

Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

1. Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
2. Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Многогранник на рисунке – это прямая призма с высотой 12.

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

(больший квадрат), (маленький прямоугольник),

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

(большой прямоугольник), (маленький прямоугольник).

Найдем площадь полной поверхности:

Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Пусть АВ = 5 см, ВС = 3 см, тогда

Из по теореме косинусов найдем ребро АС:

Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.

Теперь две задачи на площадь боковой поверхности пирамиды.

Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного получим:

(по двум катетам), тогда следовательно

Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания .

Апофему найдем по теореме Пифагора:

Как решать задачи на нахождение объема многогранника сложной формы?

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, Так как высота воды должна быть в 81 раз меньше, чем Она равна (см).

Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды

Решение.
Опустим из вершины высоту Н на основание

Диагональ основания делит его на два равных треугольника, следовательно,

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Так как точки М и К – середины АD и DС соответственно, то

Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен

Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

Больше задач на формулы объема и площади поверхности здесь.

Благодарим за то, что пользуйтесь нашими публикациями. Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Источник

Объем правильной четырехугольной пирамиды, формула

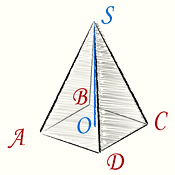
Правильная четырехугольная пирамида — это многогранник, у которого одна грань — основание пирамиды — квадрат, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр пересечения диагоналей квадрата основания из вершины.

Объем правильной четырехугольной пирамиды равен одной трети произведения площади квадрата, являющегося основанием S (ABCD) на высоту h (OS)

[ V = frac{1}{3}ha^2 ]

a — сторона квадрата – основания правильной четырехугольной пирамиды

h — высота правильной четырехугольной пирамиды

Вычислить, найти объем правильной четырехугольной пирамиды, формуле (1)

Объем правильной четырехугольной пирамиды	стр. 354

В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.

Формула вычисления объема пирамиды

1. Общая формула

Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.

• ABCD – основание;
• E – вершина;
• h – высота, перпендикулярная основанию.

2. Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Подставляем данное выражение в формулу расчета объема фигуры и получаем:

3. Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a², где а – длина его стороны.

Следовательно, формулу объема можно представить в виде:

4. Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):

С учетом этого, объем фигуры считается так:

Примеры задач

Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:

Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.

Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см² (3 см ⋅ 3 см). Следовательно, объем равен:

• Главная

• Образование

• Школьное образование
• 
  Объем четырехугольной призмы: как вычислить, формулы и примеры
  

Объем правильной треугольной пирамиды

Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle H).

( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).

Вспомним, как искать эту площадь. Используем формулу площади:

( displaystyle S=frac{1}{2}abcdot sin gamma ).

У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» — это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).

Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).

Теперь найдем ( displaystyle H).

По теореме Пифагора для ( displaystyle Delta SOC)

( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}).

Чему же равно ( displaystyle OC)? Это радиус описанной окружности в ( displaystyle Delta ABC), потому что пирамидаправильная и, значит, ( displaystyle O) — центр ( displaystyle Delta ABC).

Найдем ( displaystyle OC) (Подробнее смотри в теме «Правильный треугольник»).

( displaystyle OC=frac{2}{3}CK), так как ( displaystyle O) — точка пересечения и медиан тоже.

Подставим ( displaystyle OC) в формулу для ( displaystyle H).

( displaystyle V=frac{{{a}^{3}}}{6sqrt{2}}).