Как найти объем призмы вписанной в шар

Как найти объем призмы вписанной в шар

Решение ОГЭ по стереометрии на тему Шар из базы №332

В шар радиуса

R=sqrt11

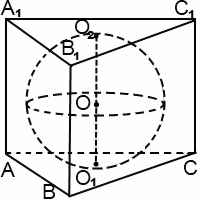
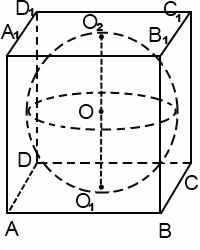
вписана правильная треугольная призма ABCDA’D’C’D’. Прямая (AB’) образует с плоскостью (ACC’) угол

45^@

. Найти объём призмы

Ответ: 36

Ключевые слова:

Стереометрия | Призма | Шар | Геометрия |

ФИПИ 2023 🔥 …

Примечание:

10%

Рейтинг сложности задачи:

Источник

Шар вписанный в призму, касается каждой ее грани. Диаметр вписанного шара равен высоте призмы, а также равен диаметру окружности, вписанной в основание призмы.

шар в призмешар, вписанный в призму

Центр шара лежит на середине высоты призмы, проведенной через центр вписанной в основание окружности. Если в основание призмы нельзя вписать окружность либо высота призмы не равна диаметру вписанной в основание окружности, то в такую призму шар вписать нельзя.

Если призма правильная, центр вписанного в нее шара является точкой пересечения бисекторных плоскостей призмы.

При решении задач на шар,вписанный в призму, можно рассмотреть сечение комбинации тел плоскостью, параллельной основаниям. Она представляет собой многоугольник, равный многоугольнику основания, с вписанной в него окружностью, радиус которой равен радиусу шара. Далее используем формулы, связывающие радиус вписанной окружности со сторонами основания, а также то, что центр вписанной в многоугольник окружности является точкой пересечения его биссектрис.

Выразим объем призмы через радиус вписанного шара — R. Объем призмы равен

    [{V_n} = {S_{ocn}} cdot H]

Площадь основания ищем по формуле S=pr, где p — полупериметр основания, r — радиус вписанной в него окружности. Поскольку в нашем случае r=R и высота призмы H=2R, то

    [{V_n} = pR cdot 2R = 2p cdot {R^2}]

Но 2p=P — периметру основания. Окончательно имеем

    [{V_n} = P{R^2}]

Выразим площадь полной поверхности прямой призмы через радиус вписанного в нее шара. Площадь полной поверхности прямой призмы равна сумме площадей оснований и боковой поверхности:

    [{S_{n.n.}} = {S_{bok}} + 2{S_{ocn}}]

Боковая поверхность

    [{S_{bok}} = PH = 2PR]

Отсюда

    [{S_{n.n.}} = 2PR + 2pR = 2PR + PR]

Таким образом, пришли к формуле

    [{S_{n.n.}} = 3PR]

Источник

Ответ:

V = R³

Объяснение:

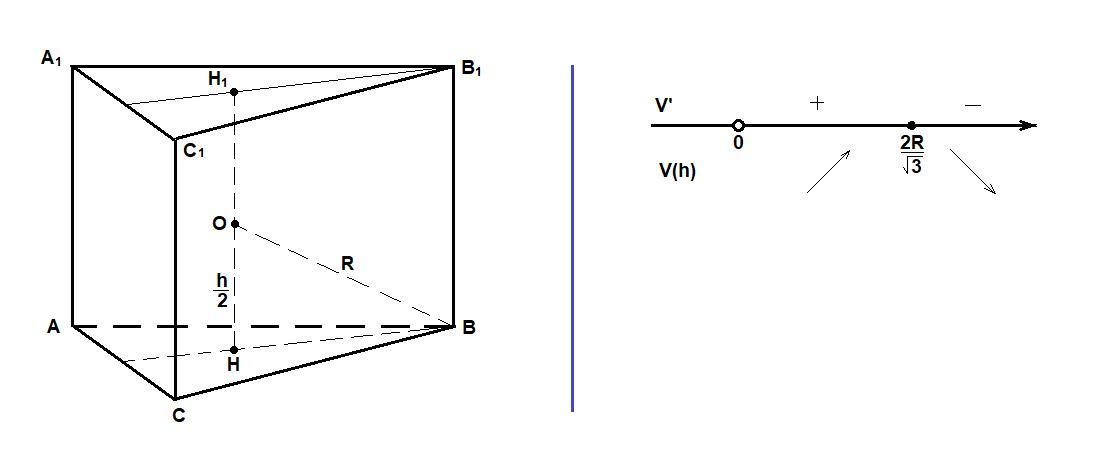
Правильная треугольная пирамида вписана в шар. Значит, центр шара лежит на середине отрезка HH₁, соединяющего центры оснований.

О – центр шара,

OB = R,

OH=dfrac{h}{2}

HB=dfrac{asqrt{3}}{3} как радиус окружности, описанной около правильного треугольника.

Из прямоугольного треугольника АВС по теореме Пифагора:

R^2=left(dfrac{asqrt{3}}{3}right)^2+left(dfrac{h}{2}right)^2

R^2=dfrac{a^2}{3}+dfrac{h^2}{4}

a^2=3R^2-dfrac{3h^2}{4}

Объем призмы:

V=S_{ABC}cdot h=dfrac{a^2sqrt{3}}{4}cdot h

Выразим объем через высоту призмы:

V=dfrac{left(3R^2-dfrac{3h^2}{4}right)cdot sqrt{3}}{4}cdot h

V=dfrac{3sqrt{3}R^2}{4}h-dfrac{3sqrt{3}}{16}h^3

Рассмотрим объем как функцию от высоты. Найдем точку максимума этой функции.

V'=dfrac{3sqrt{3}R^2}{4}-dfrac{9sqrt{3}}{16}h^2

dfrac{3sqrt{3}R^2}{4}-dfrac{9sqrt{3}}{16}h^2=0; : ; : |cdot dfrac{16}{9sqrt{3}}

dfrac{4R^2}{3}-h^2=0

h=dfrac{2R}{sqrt{3}},  

h > 0

Отметим знаки производной на интервалах (см. рисунок)

h=dfrac{2R}{sqrt{3}} – точка максимума.

Найдем объем призмы при найденном значении высоты.

V=dfrac{3sqrt{3}R^2}{4}h-dfrac{3sqrt{3}}{16}h^3=dfrac{3sqrt{3}R^2}{4}cdot dfrac{2R}{sqrt{3}}-dfrac{3sqrt{3}}{16}cdot dfrac{8R^3}{3sqrt{3}}=

=dfrac{3R^3}{2}-dfrac{R^3}{2}=R^3

Приложения:

Источник
Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

  • Все категории
  • экономические
    43,653
  • гуманитарные
    33,653
  • юридические
    17,917
  • школьный раздел
    611,926
  • разное
    16,901

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Источник



Знаток

(276),
на голосовании



5 лет назад

Голосование за лучший ответ

Михаил Ужов

Эксперт пока не указал должность



5 лет назад

В сечении, перпендикулярном боковым граням призмы и проходящем через центр шара, имеем правильный треугольник, с вписанной окружностью.
Радиус окружности R=(a²√3/4)/(3a/2)=2a√3/12=a√3/6
Сторона основания равна 6R/√3=2R√3
Высота призмы равна 2R
S=2(3R²√3)+3(2R√3×2R)=6R²√3+12R²√3=18R²√3
V=3R²√3×2R=6R³√3

Источник

Добавить комментарий