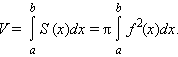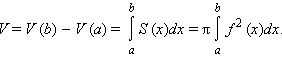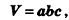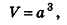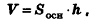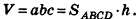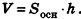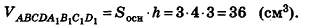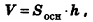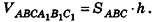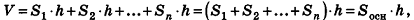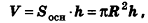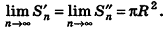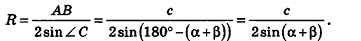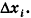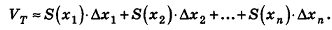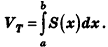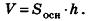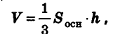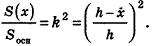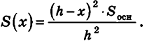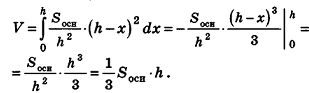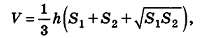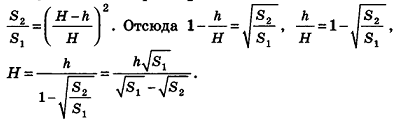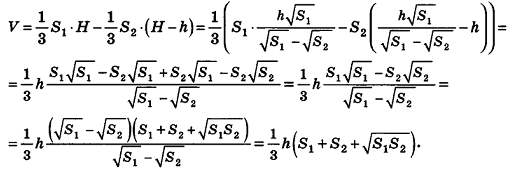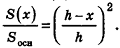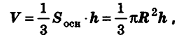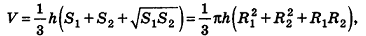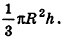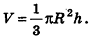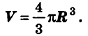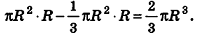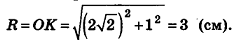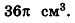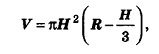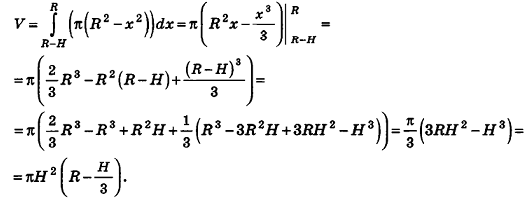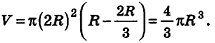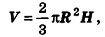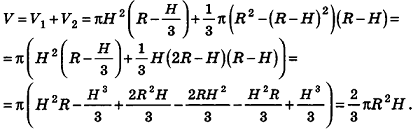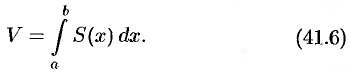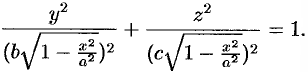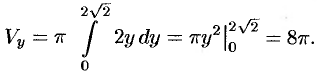Как найти объем произвольного тела

План урока:

Вычисление объема тела с помощью интеграла

Вычисление объема тел вращения

Объем наклонной призмы

Объем пирамиды

Объем конуса

Объем шара

Шаровой сегмент

Площадь сферы

Вычисление объема тела с помощью интеграла

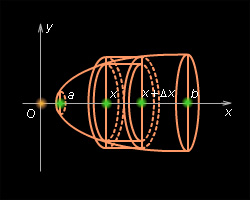
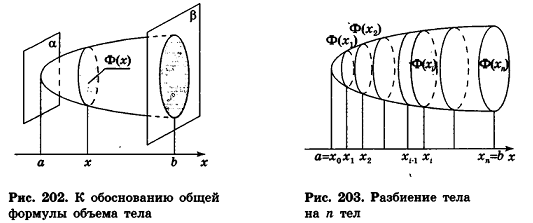
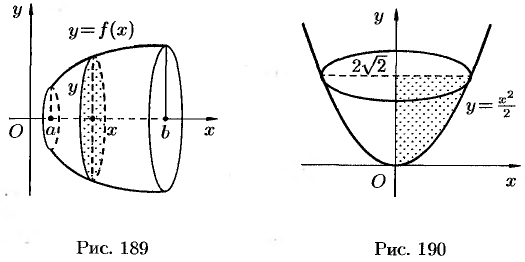
Пусть у нас есть произвольная фигура, расположенная между двумя параллельными плоскостями:

Как найти ее объем? Поступим следующим образом. Проведем прямую, перпендикулярную этим плоскостям. Эта прямая будет осью координат х. Пусть одна из плоскостей пересекает эту ось в точке а, а другая – в точке b. Таким образом, на координатной прямой появляется отрезок [a; b]. Далее разобьем этот отрезок на n равных отрезков, длина каждого из них будет равна величина ∆х. Обозначим концы этих отрезков как х₀, х₁, х₂…, х_n, причем точке х₀ будет совпадать с точкой а, а точка х_n – с точкой b. Ниже показано такое построение для n = 10:

Далее через полученные точки проведем сечения, параллельные двум плоскостям, ограничивающим фигуру. Площадь сечения, проходящую через точку с номером i, обозначим как S(x_i). Эти плоскости рассекут тело на n других тел. Обозначим объем тела, заключенного между сечениями с площадями S(x_i) и S(x_i+1) как V(x_i). Можно приближенно считать, что эти тела имеют форму прямых цилиндров (напомним, что в общем случае цилиндром необязательно считается фигура, основанием которой является круг, основание может иметь и любую другую форму). Высота всех этих цилиндров будет равна величине ∆х. Тогда объем V(x_i) может быть приближенно рассчитан так:

Общий же объем исследуемой фигуры будет суммой объемов этих прямых цилиндров:

Здесь знак ∑ означает сумму i слагаемых, каждое из которых равно величине S(x_i)•∆х. Ясно, что чем больше мы возьмем число n, тем точнее будет полученная нами формула. Поэтому будет увеличивать число n до бесконечности, тогда приближенная формула станет точной:

В правой части стоит предел суммы бесконечного числа слагаемых. Мы уже сталкивались с такими пределами, когда изучали определенный интеграл в курсе алгебры. Так как х₀ = a, а число х_n-1 при бесконечном увеличении n приближается к числу х_n, то есть к b, то можно записать следующее:

Здесь S(x) – это некоторая функция, которая устанавливает зависимость между площадью сечения объемной фигуры и координатой х, указывающей расположение этого сечения. Данная формула позволяет вычислять объем с помощью интеграла.

Итак, для вычисления объема тела необходимо:

1) выбрать в пространстве какую-то удобную ось координат Ох;

2) найти площадь произвольного сечения фигуры, проходящей перпендикулярно оси Ох через некоторую координату х;

3) найти значение чисел а и b – координат сечений, ограничивающих тело в пространстве;

4) выполнить интегрирование.

Понятно, что сразу понять, как используется эта формула, тяжело. Поэтому рассмотрим простой пример.

Задание. Фигура расположена в пространстве между двумя плоскостями, перпендикулярными оси Ох, причем координаты этих сечений равны 1 и 2. Каждое сечение фигуры с координатой х является квадратом, причем его сторона равна величине 1/х. Найдите объем тела.

Решение. В данной задаче ось Ох уже проведена. Известны и числа а и b – это 1 и 2, ведь именно плоскости, проходящие через точки х =1 и х = 2, ограничивают исследуемое тело. Теперь найдем площадь произвольного сечения с координатой х. Так как оно является квадратом со стороной 1/х, то его площадь будет квадратом этой стороны:

Вычисление объема тел вращения

Телом вращения называют тело, которое может быть получено вращением какой-то плоской фигуры относительно некоторой оси вращения. Например, цилиндр получают вращением прямоугольника вокруг одной из его сторон, а усеченный конус – вращением прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.

В задачах на вычисление объемов таких тел ось координат Ох уже задана естественным образом – это ось вращения тела. Ясно, что каждое сечение тела, перпендикулярное оси вращения, будет являться кругом.

Рассмотрим случай, когда вокруг оси Ох поворачивают график некоторой функции у = f(x), ограниченный прямыми х = а и у = b. Тогда получится тело, сечениями которого являются круги, причем их радиусы будут равны величине f(x). Напомним, что площадь круга вычисляют по формуле:

Рассмотрим, как на практике используется эта формула.

Задание. Объемное тело получено вращением ветви параболы

вокруг оси Ох. Оно ограничено плоскостями х = 0 и х = 4. Каков объем такой фигуры?

Решение. Здесь пределами интегрирования, то есть числами а и b, будут 0 и 4. Используем формулу для тела вращения:

Объем наклонной призмы

Теперь, используя методы интегрирования, мы можем составить формулы для вычисления объема некоторых фигур. Начнем с треугольной наклонной призмы.

Пусть есть треугольная призма АВСА₂В₂С₂. Проведем ось Ох так, чтобы точка О располагалась в плоскости АВС. Пусть Ох пересечет плоскость А₂В₂С₂ в некоторой точке О₂. Тогда отрезок ОО₂ будет высотой призмы, ведь он окажется перпендикулярным к обоим основаниям.

Обозначим длину высоты ОО₂ буквой h. Далее докажем, что всякое сечение А₁В₁С₁ призмы, перпендикулярное оси Ох, будет равно ∆АВС. Действительно, если АВС⊥ОО₂ и А₁В₁С₁⊥ОО₂, то АВС||А₁В₁С₁. Прямые АВ и А₁В₁ принадлежат одной грани АВВ₂А₁, но не пересекаются, ведь они находятся в параллельных плоскостях. Аналогично АС||А₁С₁ и ВС||В₁С₁. Теперь посмотрим на четырехугольник АВВ₁А₁. АВ||A₁В₁ и АА₁||ВВ₁. Тогда АВВ₁А₁ по определению является параллелограммом. Это означает, что отрезки АВ и А₁В₁ одинаковы. Аналогично доказывается, что одинаковы отрезки АС и А₁С₁, а также ВС и В₁С₁. Но тогда одинаковы и ∆АВС и ∆А₁В₁С₁.

Итак, площади всех сечений одинаковы и равны площади основания призмы. Обозначим ее как S. Так как S не зависит от координаты, то интегрирование будет выглядеть так:

Итак, объем треугольной наклонной призмы – это произведение площади ее основания на высоту. Теперь рассмотрим произвольную призму, в чьем основании находится n-угольник. Такой n-угольник можно разбить на треугольные призмы с общей высотой h и площадями оснований S₁, S₂, S₃, …

Тогда площадь S основания всей призмы будет суммой этих чисел:

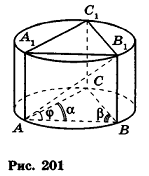
Задание. Основание призмы – это треугольник со сторонами 10, 10 и 12. Боковое ребро имеет длину 8 и образует с основанием угол в 60°. Вычислите объем призмы.

Решение. Пусть в основании призмы АВСА₁В₁С₁ лежит ∆АВС со сторонами АВ = 12 и АС = ВС = 10. Его площадь можно найти разными способами, но быстрее всего применить формулу Герона. Сначала найдем полупериметр ∆АВС:

Далее надо найти высоту призмы. Опустим из точки В₁ перпендикуляр В₁О на плоскость АВС. Тогда в прямоугольном ∆ОВВ₁ ∠В = 60° (по условию задачи и по определению угла между плоскостью и прямой). Зная длину бокового ребра ВВ₁, найдем высоту ОВ₁:

Объем пирамиды

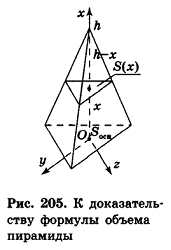
Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.

Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.

Далее построим сечение А₁В₁С₁, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ₁. Тогда ОМ₁ – это координата х, характеризующая расположение сечения А₁В₁С₁.

Осталось составить выражение для площади ∆А₁В₁С₁. Так как АВ||A₁B₁, то ∠АВО и ∠А₁В₁О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А₁В₁О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что

Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ₁В₁. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому

Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:

Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S₁, S₂, S₃…, которые в сумме составляют площадь многоугольника S.

Объем треугольных пирамид рассчитывается по выведенной нами формуле:

Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.

Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:

Задание. В кубе АВСDA₁В₁С₁D₁ отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С₁EFC меньше объема куба?

Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:

Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?

Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.

Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.

Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А₁В₁С₁, параллельное основанию.

Обозначим площадь нижнего основания пирамиды как S₂, а площадь верхнего основания – как S₁. Далее высоту усеченной пирамиды (отрезок ММ₁) обозначим как h. Мы уже выяснили ранее, что основания АВС и А₁В₁С₁ – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ₁. Тогда можно записать:

Далее используем основное свойство пропорции:

Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:

Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.

Сначала вычислим площади оснований:

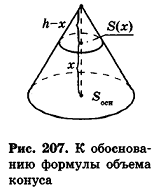
Объем конуса

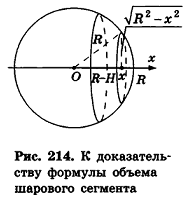
Рассмотрим конус с высотой h и радиусом основания R. Совместим начало координат с вершиной конуса и направим ось Ох в сторону основания конуса. Тогда она пересечет основание в какой-то точке М c координатой h. Далее через точку М₁ на оси Ох, имеющей координату х, проведем сечение, перпендикулярное оси Ох. Это сечение будет окружностью.

Также построим образующую ОА, которая будет проходить через сечение в точке А₁. Теперь сравним ∆ОАМ и ∆ОА₁М₁. Они прямоугольные, и у них есть общий угол ∠АОМ. Это значит, что они подобны, и поэтому справедливо отношение:

Полученную формулу можно переписать в другом виде так, чтобы она содержала площадь основания, причем она будет похожа на аналогичную формулу для пирамиды:

Задание. Радиус конуса – 8 см, а его высота составляет 12 см. Определите его объем.

Решение. Здесь надо просто применить выведенную формулу:

Задание. В сосуде, имеющем форму перевернутого конуса, вода доходит до уровня, соответствующего 2/3 высоты сосуда. При этом ее объем составляет 192 мл. Каков объем всего сосуда?

Решение. В задаче фигурируют два конуса. Один из них – это сам сосуд, а второй – его часть, заполненная водой. При выведении формулы объема мы уже выяснили, что радиусы таких конусов пропорциональны их высотам:

Мы уже заметили, что формулы для объема пирамида и конуса идентичны. По сути, конус можно рассматривать как особый случай пирамиды, у которой в основании лежит не многоугольник, а окружность. Аналогично и усеченный конус можно считать особым случаем усеченной пирамиды, а поэтому для расчета его объема можно применять такую же формулу:

Задание. Вычислите объем усеченного конуса с высотой 9 и радиусами оснований 7 и 4.

Решение. Сначала находим площади оснований:

Объем шара

Пришло время разобраться и с таким телом, как шар. Здесь можно использовать тот же метод интегрирования, что и в случае с конусом и пирамидой. Но можно поступить и иначе – использовать выведенную нами для тел вращения формулу

Шар как раз является телом вращения. Он получается при вращении полуокружности вокруг диаметра, на который эта дуга опирается.

Напомним известное нам уравнение окружности, чей центр совпадает с началом координат:

Здесь надо уточнить, что если у получившейся функции впереди записан знак «+», то ее график соответствует полуокружности, находящейся над осью Ох. Если же используется знак «–», то получается уже нижняя полуокружность, расположенная под осью Ох:

В принципе мы можем поворачивать любую из этих полуокружностей вокруг Ох, но мы выберем верхнюю полуокружность. Заметим, что эта дуга начинается в точке х = – R и заканчивается в точке х = R, эти числа будут пределами интегрирования. Тогда объем шара равен:

Задание. Найдите объем шара с радиусом 6.

Решение. Подставляем радиус из условия в формулу:

Задание. В цилиндр вписан шар. Во сколько раз объем цилиндра больше объема такого шара?

Решение. Ясно, что так как шар вписан в цилиндр, то радиусы этих тел одинаковы. Обозначим этот радиус как R. Также ясно, что раз шар касается оснований цилиндра, то расстояние между ними (то есть высота цилиндра) равно двум радиусам шара:

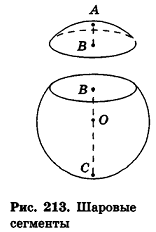
Шаровой сегмент

Когда плоскость проходит через шар, она рассекает его на две фигуры, которые именуются шаровым сегментом. Если из центра шара О провести радиус ОА длиной R в направлении плоскости сечения, который перпендикулярен этой плоскости, то он пересечет ее какой-то точке В. Длину отрезка АВ называют высотой шарового сегмента и обозначают буквой h:

Ясно, что при этом отрезок ОВ – это расстояние от секущей плоскости (или от основания сегмента) до центра шара, причем этот отрезок имеет длину R –h.

Можно считать, что шаровой сегмент, как и шар, получается при вращении дуги окружности вокруг оси Ох. Однако если сам шар при этом ограничен плоскостями x = R и х = – R, то сегмент ограничен другими плоскостями: х = R и х = R – h. Это значит, что его объем можно вычислить с помощью интеграла также, как и объем шара, отличаться будет лишь нижний предел интегрирования:

Заметим, что шар можно рассматривать как шаровой сегмент, чья высота вдвое больше его радиуса. И действительно, если в выведенную формулу мы подставим значение h = 2R, то получим уже известную нам формулу объема шара.

Задание. Найдите объем шарового сегмента высотой 6, если он отсечен от шара радиусом 15.

Решение. Используем выведенную формулу:

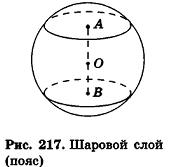
Задание. Диаметр шара разделили на три равных отрезка. Через концы этих отрезков провели секущие плоскости, перпендикулярные диаметру. Чему равен объем тела, заключенного между этими двумя плоскостями (оно называется шаровым слоем), если радиус шара обозначен буквой R?

Решение. Ясно, что для вычисления объема шарового слоя достаточно вычесть из объема шара объемы двух шаровых сегментов, образующихся при проведении секущих плоскостей. Так как они разделили диаметр на три одинаковых отрезка, то высота этих сегментов будет в три раза меньше диаметра шара:

Площадь сферы

В предыдущих уроках мы уже узнали формулу для вычисления площади сферы, однако тогда мы ее не доказывали. Однако теперь мы можем ее доказать, используя формулу объема шара. Но сначала напомним саму формулу:

Впишем сферу в многогранник с n гранями. Ясно, что расстояние от граней этого многогранника до центра сферы равно радиусы сферы R. Далее построим пирамиды, чьи вершины находятся в центре сферы, а основания – это грани многогранника. Заметим, что такие пирамиды будут иметь одинаковые высоты длиной R.

Обозначим площади граней многогранника как S₁, S₂, S₃,…S_n. Тогда объемы пирамид, построенных на этих гранях, вычисляются так:

Заметим, что в сумме эти объемы дают объем всего многогранника, а сумма площадей S₁, S₂, S₃,…S_n – это площадь всей его поверхности. Тогда можно записать:

Теперь начнем неограниченно уменьшать размеры граней многогранника. Тогда число n будет расти, объем многогранника будет приближаться к объему шара, а площадь многогранника – к площади к сфере. Тогда и доказанное равенство можно будет записать так:

Задание. Необходимо изготовить закрытый сосуд с заранее заданным объемом V. Предлагается два варианта формы этого сосуда – шар и куб. Так как поверхность сосуда покрывается очень дорогой краской, то необходимо выбрать вариант с меньшей площадью поверхности. Какую форму для сосуда следует выбрать?

Решение. Обозначим радиус шара как R, а ребро куба как а. Тогда можно записать:

Теперь надо выяснить, какое из полученных значений больше. Для этого поделим площадь куба на площадь сферы. Если получится число, большее единицы, то площадь куба больше:

Получившееся число больше единицы, ведь 6 больше числа π, равного 3,1415926… Значит, и площадь куба больше, а потому необходимо выбрать сосуд, имеющий форму шара.

Ответ: шар.

Примечание. Более сложными математическими методами можно доказать, что если второй сосуд имеет не форму куба, а вообще любую форму, отличную от шара, то всё равно следует выбирать именно сосуд в форме шара. То есть из всех поверхностей, ограничивающих определенный объем, именно сфера имеет наименьшую площадь. Этот факт имеет и физическое следствие – капли дождя и мыльные пузыри стремятся принять форму шара, также как и любые жидкости, находящиеся в невесомости.

Итак, мы научились вычислять объемы таких тел, как конус, пирамида, шар, призма. Также помощью интегрирования можно находить объемы и ещё более сложных тел, если мы можем составить функцию, описывающую площадь их сечения.

Объём
произвольного тела может быть вычислен
с помощью интегрального исчисления.

Если
задано тело вращения заданное функцией
y = f(x), то его объём можно определить по
формуле

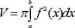
34.Объем тела вращения.

Объем
тела вращения равен 

Придадим x приращение Δx > 0 (x + Δx < b).
Построим два цилиндра с общей
высотой Δx (рис. 7.2.2).
Меньший цилиндр имеет своим основанием
круг площадью S (x),
а больший – круг площадью S (x + Δx).
Если ΔV –
прирост объема тела вращения,
то S (x)Δx < ΔV < S (x + Δx)Δx,
откуда 

Поскольку
функция f (x) непрерывна,
то непрерывна и функция 

следовательно, 

Переходя
к пределу в двойном неравенстве, имеем 

то
есть V’ (x) = S (x).

Объем V (x) является
первообразной для функции S (x) на
промежутке [a; b].
Отсюда имеем 

35.Площадь поверхности вращения

Поверхность
вращения — поверхность,
образуемая при вращении вокруг прямой
(оси поверхности) произвольной линии
(прямой,
плоской или пространственной кривой).
Например, если прямая пересекает ось
вращения, то при её вращении
получится коническая поверхность,
если параллельна оси — цилиндрическая,
если скрещивается с осью —
однополостныйгиперболоид
вращения.
Одна и та же поверхность может быть
получена вращением самых разнообразных
кривых. Площадь
поверхности вращения,
образованной вращением плоской кривой
конечной длины вокруг оси, лежащей в
плоскости кривой, но не пересекающей
кривую, равна произведению длины кривой
на длину окружности с радиусом, равным
расстоянию от оси до центра
масс кривой.
Это утверждение называется второй теоремой
Гюльдена,
или теоремой Паппа о центроиде.

Площадь
поверхности вращения,
образованной вращением кривой 
 вокруг
оси 
 можно
вычислить по формуле

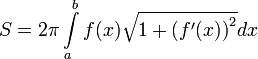
Площадь
поверхности вращения,
образованной вращением кривой 
 вокруг
оси 
можно
вычислить по формуле

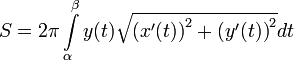
Для
случая, когда кривая задана в полярной
системе координат 
 действительна
формула

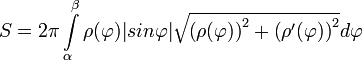
36. Механические приложения определённого интеграла (работа сил, статические моменты, центр тяжести).

Вычисление
работы сил

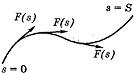
Материальная
точка движется по непрерывно
дифференцируемой кривой, при этом на
нее действует сила, направленная по
касательной к траектории в направлении
движения. Полная работа, совершаeмая
силой F(s):

Если
положение точки на траектории движения
описывается другим параметром, то
формула приобретает вид:

Вычисление
статических моментов и центра тяжести

Пусть
на координатной плоскости Оху некоторая
масса М распределена с плотностью р =
р(у) на некотором множестве точек S (это
может быть дуга кривой или ограниченная
плоская фигура). Обозначим s(у) – меру
указанного множества (длина дуги или
площадь).

Определение
2. Число 
 называется
k-м моментом массы М относительно оси
Ох.

При
k = 0 М₀ =
М – масса,

k
= 1 М₁ –
статический момент,

k
= 2 М₂ –
момент инерции.

Аналогично
вводятся моменты относительно оси Оу.
В пространстве подобным же образом
вводятся понятия моментов массы
относительно координатных плоскостей.

Если
р = 1, то соoтветствующие моменты называются
геометрическими. Координаты центра
тяжести однородной (р – const) плоской
фигуры определяются по формулам:

где
М₁^y,
М₁^x –
геометрические статические моменты
фигуры относительно осей Оу и Ox; S –
площадь фигуры.

37.
n-мерное
евклидово пространство.

Определение
1. Упорядоченная последовательность n
действительных чисел {х₁,
х₂;…;
х_n}
называется точкой п- мерного пространства,
при этом числа x_i,
i = 1,…, n называются координатами
точки.

Обозначение:
X = (х₁,
х₂;…;
х_n).

Определение
2. Если для любых двух точек X = (х₁,
х₂;…;
х_n)
и У = (y₁,
y₂;…;
y_n)
n-мерного пространства определено
расстояние между ними по формуле

,

то
такое пространство называется n-мерным
евклидовым.

Обозначение:
Еⁿ.

Определение
3. Пусть X – фиксированная точка пространства
Еⁿ; 
 >
0 – произвольное положительное число.
Множество точек Y пространства Еⁿ таких,
что

р(Х;
Y) ,

называется
n-мерным шаром с центром в точке X и
радиусом 
 или
просто 
-окрестностъю
точки X в пространстве Еⁿ.

Определение
4. Если существует отображение множества
натуральных чисел в множество точек
пространства Еⁿ

то
множество точек Х₁;
Х₂;
… называется последовательностью точек
этого пространства.

Обозначение:
{Х_m}.

Определение
5. Точка X 
 Еⁿ называется
пределом последовательности {Х_m},
если

Определение
6. Пусть Е 
 Еⁿ –
некоторое подмножество n-мерного
евклидова пространства. Отображение
точек множества Е в множество действительных
чисел R называется функцией п
переменных.

Обозначение:
у = f(х₁,
х₂;…;
х_n);
у = f(Х).

Множество
Е называется областью определения
функции n переменных.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

Объёмы поверхностей геометрических тел:

То, чем в предыдущие эпохи занимались только зрелые умы ученых мужей, в более позднее время стало доступным для понимания юношей.

С древних времен люди применяли геометрию для решения конкретных житейских проблем — нахождения объемов сосудов, строений и кораблей, количества краски, необходимой для ремонта помещения. На основании практического опыта были разработаны методы вычисления объемов тел и площадей поверхностей. Но нахождение соответствующих формул, а тем более их доказательств заняло немало страниц в истории геометрической науки. Многие выдающиеся ученые внесли свой вклад в развитие теории объемов, а популяризаторы математики — в упрощение и доступное изложение этой теории.

Основной целью данной главы является формирование представлений об объемах и площадях поверхностей, обоснование соответствующих формул для основных пространственных фигур. Вы. научитесь использовать различные методы нахождения объемов, как строго геометрические, так и те, которые объединяют в себе геометрию и начала анализа. При изучений объемов тел полезно будет вспомнить и систематизировать материал о площадях фигур на плоскости. Подходы, которые применялись для получения основных формул площадей, будут надежным фундаментом для построения теории объемов.

В данной главе речь пойдет о всех основных фигурах, которые вы изучали в течение года, в частности о тесной связи многогранников и тел вращения. Это даст вам возможность, с одной стороны, вспомнить основные факты из курса геометрии, а с другой — на основании формул для площадей поверхностей многогранников получить соответствующие результаты для тел вращения.

Задачи данной главы содержат много геометрических конфигураций, что позволит вам переосмыслить весь курс стереометрии с точки зрения применения своих знаний на практике, в частности для нахождения, пожалуй, самых распространенных в жизни геометрических величин — объемов и площадей поверхностей. Ради этого бесценного опыта вы и изучали, в конце концов, геометрию в пространстве.

Объемы

Понятие объема хорошо известно на уровне повседневного опыта: мы покупаем пакет сока определенного объема, рассчитываем, какой объем займет в квартире новая мебель, берем для приготовления блюда кастрюлю соответствующего объема. Придадим этим наглядным представлениям об объеме тела определенную математическую строгость.

Понятие объема многогранников

Для дальнейших рассуждений полезно объединить практический опыт и известную уже теорию площадей многоугольников. По аналогии с ней мы и будем строить теорию объемов пространственных тел, в первую очередь многогранников.

Объем характеризует величину части пространства, которую занимает геометрическое тело, и измеряется, как и площадь, в определенных единицах. Единицей измерения площадей является площадь единичного квадрата, а за единицу измерения объема принимается объем единичного куба, то есть куба, ребро которого равно единице длины. Например, если за единицу измерения длины принимается 1 мм, 1 см, 1 дм или 1 м, то за единицу измерения объема принимается объем куба с ребром 1 мм, 1 см, 1 дм или 1 м. Соответствующая единица объема называется кубическим миллиметром (1 мм³), кубическим сантиметром (1 см³), кубическим дециметром или литром (1 дм³ или 1 л), кубическим метром (1 м³). Таким образом, вычисление объемов тел разной формы основано на сравнении с объемом единичного куба.

Измерить объем тела на практике можно, например, погрузив его в воду и подсчитав количество вытесненной телом воды. Но во многих случаях это не целесообразно, поэтому очень полезно вывести и научиться применять формулы для вычисления объемов. Соответствующая теория основана на аксиомах объема многогранников.

1. Равные многогранники имеют равные объемы.
2. Бели многогранник составлен из нескольких многогранников, то его объем равен сумме объемов этих многогранников.
3. Объем куба с ребром, равным единице длины, равен единице объема.

Итак, объем многогранника — это положительная величина, Числовое значение которой удовлетворяет аксиомам объема. : – Как правило, объем обозначают буквой V.

Приведенные аксиомы имеют и практическую основу. Действительно, все пакеты, имеющие форму прямоугольного параллелепипеда и одинаковые размеры, содержат одинаковое количество сока.

Тела, имеющие равные объемы, называются равновеликими.

Если же каждый из двух пакетов можно разлить в одинаковое количество маленьких пакетиков, то сумма объемов этих пакетиков будет равна объему каждого из них, то есть данные пакеты имеют одинаковый объем.

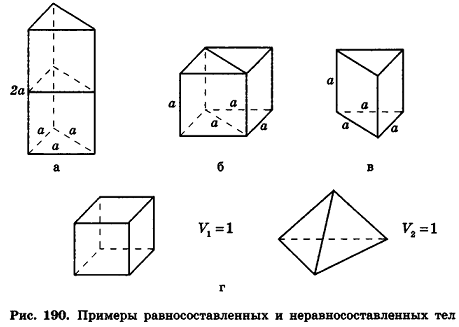
Тела, составленные из одних и тех же многогранников, называются равносоставленными. Например, равносоставленными будут тела, изображенные на рисунке 190, а, б: прямая треугольная призма и прямой параллелепипед. Действительно, каждая из этих фигур составлена из двух одинаковых прямых призм, таких как на рисунке 190, в.

Очевидно, что объемы равносоставленных многогранников равны по второй аксиоме. Интересно, что обратное утверждение неверно (в отличие от аналогичной теоремы для площадей). Так, многогранники равного объема не всегда можно разбить на конечное число равных многогранников. В частности, куб и правильный тетраэдр равных объемов (рис. 190) не являются равносоставленными.

Объем параллелепипеда

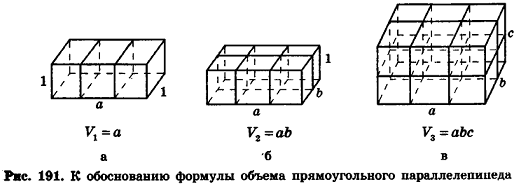
Простейшей фигурой с точки зрения вычисления объема является прямоугольный параллелепипед.

Теорема (формула объема прямоугольного параллелепипеда)

Объем прямоугольного параллелепипеда равен произведению трех его измерений:

где 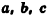— измерения прямоугольного параллелепипеда.

Приведем рассуждения, на которых основано доказательство данной теоремы.

Сначала рассмотрим прямоугольный параллелепипед с измерениями а, 1, 1. Так как в отрезке а единица измерения длины помещается а раз, то единичный куб помещается в параллелепипед также а раз. Значит, объем прямоугольного параллелепипеда равен а (рис. 191, а).

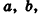
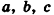
Аналогично объем прямоугольного параллелепипеда с измерениями 1 равен (рис. 191, б), а прямоугольного параллелепипеда с измерениями — равен abc (рис. 191, в).

Полное доказательство данной теоремы приведено в Приложении 2.

Следствие (формула объема куба)

Объем куба равен кубу его ребра:

где а – ребро куба.

Нам известно, что площадь прямоугольника равна произведению двух его измерений, а параллелограмма — произведению его стороны на проведенную к ней высоту. По аналогии нетрудно предположить, что объем произвольного параллелепипеда также можно найти через площадь основания и соответствующую высоту.

Теорема (формула объема параллелепипеда)

Объем параллелепипеда равен произведению площади его основания на высоту:

где 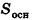— площадь основания параллелепипеда, h — высота.

Доказательство:

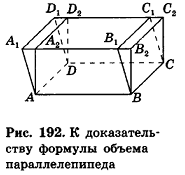
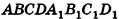
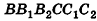
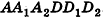
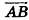
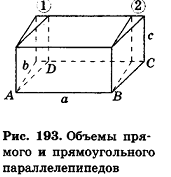
Очевидно, что для прямоугольного параллелепипеда данная формула верна. Докажем ее для наклонного параллелепипеда (рис. 192). Проведем через ребра ВС и AD плоскости, перпендикулярные основанию ABCD. Дополним наклонный параллелепипед треугольной призмой и отсечем треугольную призму Эти призмы равны, так как совмещаются параллельным переносом на вектор . Значит, полученный параллелепипед имеет тот же объем, что и исходный.

При описанном преобразовании параллелепипеда площадь его основания и высота сохраняются, а две боковые грани становятся перпендикулярными плоскости основания ABC. Если выполнить аналогичное преобразование с помощью плоскостей, проходящих через АВ и DC перпендикулярно основанию ABCD, получим прямой параллелепипед с основанием ABCD, равновеликий исходному. При этом высоты параллелепипедов также сохраняются.

Теперь проведем через точки А я В плоскости, перпендикулярные АВ (рис. 193). Дополняя прямой параллелепипед одной треугольной призмой (I) и отсекая равную ей другую призму (2), получим прямоугольный параллелепипед, равновеликий предыдущему.

Объем полученного прямоугольного параллелепипеда равен 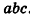. Так как при описанных выше преобразованиях данного параллелепипеда в прямоугольный каждый раз образуется параллелепипед, равновеликий предыдущему, а площадь

основания и высота сохраняются, то и объем исходного параллелепипеда можно вычислить с помощью полученной формулы. Итак, объем наклонного параллелепипеда

Таким образом, объем произвольного параллелепипеда вычисляется по формуле

Теорема доказана.

Пример №1

В основании наклонного параллелепипеда лежит прямоугольник со сторонами 3 см и 4 см. Боковое ребро параллелепипеда равно 6 см. Найдите объем данного параллелепипеда, если две его боковые грани перпендикулярны плоскости основания, а две другие наклонены к ней под углом 30°.

Решение:

Пусть дан параллелепипед 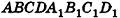(рис. 194), в основании которого лежит прямоугольник ABCD со сторонами 3 см и 4 см. Боковые ребра параллелепипеда равны и имеют длину б см. Противолежащие боковые грани параллелепипеда параллельны, следовательно, наклонены к плоскости его основания под равными углами.

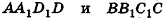
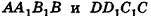
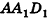
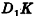
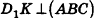
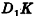
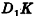
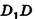
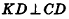
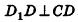
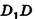
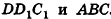
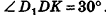
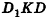
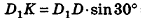
Пусть грани перпендикулярны грани ABCD, а грани образуют с ABCD угол 30°. Проведем в плоскости перпендикуляр к AD. По свойству перпендикулярных плоскостей , следовательно, — высота данного параллелепипеда. Так как является перпендикуляром, — наклонной, KD — ее проекцией на плоскость ABC, причем , то по теореме о трех перпендикулярах . Значит, угол равен углу между плоскостями . По условию . Из прямоугольного треугольника получим: = 3 см.

Таким образом,

Ответ: 36 см³.

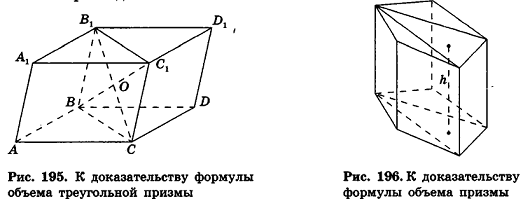
Объем призмы

На плоскости для получения формулы площади треугольника было удобно дополнить треугольник до параллелограмма. Далее, для получения формулы площадей других многоугольников, целесообразно было разбить их на треугольники. Применим аналогичные приемы для вывода формулы объема призмы.

Теорема (формула объема призмы)

Объем призмы равен произведению площади ее основания на высоту:

где — площадь основания призмы, h — ее высота.

Доказательство:

Пусть дана треугольная призма . Дополним ее до параллелепипеда , как показано на рисунке 195. Дополняющая призма симметрична данной относительно центра симметрии параллелепипеда точки О. Значит, она равна данной призме. Тогда, по аксиомам объема, объем параллелепипеда равен удвоенному объему данной призмы. Но значит,

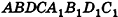
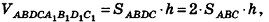
Применим только что выведенную формулу объема треугольной призмы к рассмотрению произвольной призмы.

Разобьем основание призмы на треугольники, а призму — на соответствующие треугольные призмы с высотой h (рис. 196).

По аксиоме, объем данной призмы равен сумме объемов составляющих ее треугольных призм:

где 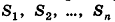— площади треугольников, на которые разбито основание призмы.

Теорема доказана.

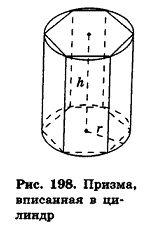
Пример №2

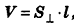
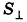
Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения: , где I — боковое ребро призмы, — площадь перпендикулярного ему сечения. Докажите.

Решение:

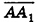
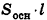
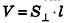
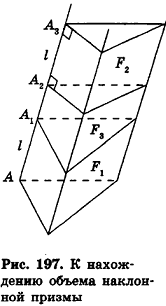
Рассмотрим наклонную призму F₁ с ребром АА₁ = I (рис. 197). Проведем два ее перпендикулярных сечения, расстояние между плоскостями которых I и которые не имеют с данной призмой общих точек. При этом получим прямую призму F₂ и многогранник F₃ (рис. 197). Многогранник, гранник, как совмещаются параллельным переносом на вектор . Поэтому их объемы равны. Эти многогранники имеют общую часть F₃. Отсюда по аксиоме объема следует, что объемы призм F₁ и F₂ также равны. Но последняя призма является прямой, и ее объем равен . Значит, объем данной призмы равен .

Объем цилиндра

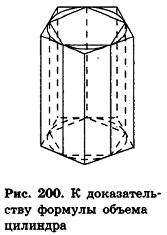
При обосновании формулы площади круга в планиметрии мы использовали вписанные в окружности и описанные около них многоугольники. Применим аналогичные рассуждения и в пространстве, заменив круг на цилиндр, а многоугольники — на призмы. Дадим соответствующие определения.

Определение:

Прямая призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра.

При этом цилиндр называется описанным около призмы. Очевидно, что боковые ребра призмы — образующие цилиндра, а высоты прямой призмы и описанного около нее цилиндра равны (рис. 198).

Определение:

Прямая призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра.

При этом цилиндр называется вписанным в призму (рис. 199). Очевидно, что высоты прямой призмы и вписанного в нее цилиндра равны.

Теорема (формула объема цилиндра)

Объем цилиндра равен произведению площади его основания на высоту:

где 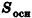— площадь основания цилиндра, h — высота, R — радиус цилиндра.

Доказательство:

Впишем в данный цилиндр радиуса R и высоты h правильную п-угольную призму с площадью основания S’_n и опишем около него правильную n-угольную призму с площадью основания 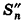(рис. 200). Тогда, по доказанному при обосновании формулы для площади круга,

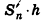
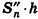
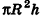
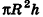
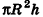
Отсюда следует, что при неограниченном возрастании п объемы вписанных призм и объемы описанных призм стремятся к величине . Значит, существуют призмы, содержащиеся в данном цилиндре, и призмы, содержащие его, объемы которых сколь угодно мало отличаются от . Тогда объем цилиндра выражается формулой V = .

Теорема доказана.

Пример №3

Основание прямой призмы — треугольник со стороной с-и прилежащими к ней углами 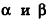. Диагональ грани, содержащей сторону с, образует с плоскостью основания призмы угол ф. Найдите объем цилиндра, описанного около призмы.

Решение:

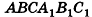
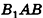
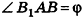
Пусть дана прямая треугольная призма , в основании которой лежит треугольник . Так как , то — наклонная, АВ — ее проекция на плоскость ABC. Значит, по определению угол равен углу между АВ и плоскостью ABC. По условию (рис. 201).

Рассмотрим цилиндр, описанный около данной призмы. Его основания описаны около оснований призмы, высота равна высоте призмы.

По теореме синусов для треугольника ABC имеем:

Из прямоугольного треугольника

Следовательно, объем цилиндра равен:

Ответ:

Объемы пирамиды, конуса и шара

Рассмотрим способ вычисления объемов тел, в основе которого лежит понятие интеграла, известное из курса алгебры и начал анализа.

Общая формула объема

Пусть тело Т, объем которого требуется вычислить, расположено между двумя параллельными плоскостями . Введем систему координат так, чтобы ось Ох была перпендикулярна плоскостям (рис. 202). Пусть плоскость а задана уравнением х = а, а плоскость — х = Ь (а<Ь).

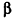
Будем рассматривать случай, когда любое сечение тела Ф(х) плоскостью, перпендикулярной-оси Ох и пересекающей эту ось в точке (х;0;0), является кругом или многоугольником (такой случай возможен, если Ф(х) — точка).

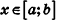
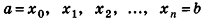
Обозначим площадь фигуры Ф(х) через S(x). Допустим, что S(x) — непрерывная функция при . Разобьем отрезок [a;b] на n равных отрезков точками и через точки с абсциссами х, проведем плоскости, перпендикулярные оси Ох (рис. 203).

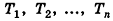
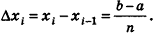
Эти плоскости разобьют тело Т на n тел: . Если сечение Ф(х₁) — круг, то объем тела Т, приближенно равен объему цилиндра с основанием Ф(х₁) и высотой Если сечение Ф(х₁) — многоугольник, то объем тела T_i приближенно равен объему прямой призмы с основанием ф(х, ) и высотой

Учитывая, что объем цилиндра и призмы равен произведению площади основания на высоту, то есть 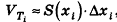получаем:

При неограниченном возрастании n правая часть данной формулы приближается сколь угодно близко к объему тела Т. С другой стороны, так как S(x) непрерывна на 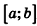, это же выражение приближается к соответствующему интегралу. Итак,

Таким образом, мы получили формулу для вычисления объема тела с помощью интеграла. Будем называть ее интегральной формулой объема.

Из этой формулы вытекает интересное и удобное в применении следствие, формулировка которого принадлежит итальянскому математику Бонавентуре Кавальери.

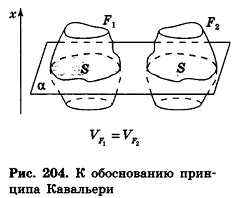
Принцип Кавальери

Если при пересечении двух тел F₁ и F₂ плоскостями, параллельными одной и той же плоскости а, в сечениях получаются фигуры с равными площадями, то объемы данных тел равны.

Это утверждение легко вывести из интегральной формулы объема, если расположить систему координат так, чтобы ось Ох была перпендикулярна плоскости а (рис. 204). Применение интеграла и принципа Кавальери позволяет значительно упростить нахождение формул, выражающих объемы многих важных тел.

Объем пирамиды и конуса

В пунктах 15.3 и 15.4 мы установили, что объемы призмы и цилиндра определяются одной и той же формулой:

Поэтому вполне естественно предположить, что будут совпадать формулы для объемов пирамиды и конуса.

Теорема (формула объема пирамиды)

Объем пирамиды равен трети произведения площади основания на высоту:

где — площадь основания пирамиды, h — высота.

Доказательство:

Разместим пирамиду в системе координат так, чтобы ось Ох была направлена вдоль высоты, а основание’ принадлежало бы плоскости 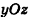(рис. 205). Пусть некоторая плоскость параллельна основанию пирамиды и пересекает ее высоту в точке (х;0;0). Обозначим через S(x) площадь сечения пирамиды этой плоскостью. По доказанному в п. 10.2 она отсекает пирамиду, подобную данной. В частности, подобными являются многоугольники основания и сечения. Пусть k — коэффициент подобия. Тогда

Отсюда

Применяя теперь для пирамиды интегральную формулу объема, получим:

Теорема доказана.

Следствие (формула объема усеченной пирамиды)

Объем усеченной пирамиды вычисляется по формуле:

где h – высота усеченной пирамиды, 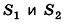площади ее оснований.

Доказательство:

Дополним данную усеченную пирамиду до полной с высотой Н (рис. 206). Тогда высота дополняющей пирамиды будет равна H-h. Из подобия полной и дополняющей пирамид, площади оснований которых равны 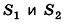соответственно, получаем:

По аксиомам объема, объем усеченной пирамиды равен разности объемов полной и дополняющей пирамид. Следовательно,

Формула доказана.

Заметим, что при доказательстве теоремы об объеме пирамиды и ее следствия, кроме интегральной формулы объема, мы применили только тот факт, что плоскость, параллельная основанию, отсекает пирамиду, для площади основания S(x) и высоты h-x которой верна формула

Но эта формула, по доказанному в п. 13.2, также верна и для конуса (рис. 207). Поэтому аналогичными формулам объема и их доказательствам для пирамиды и усеченной пирамиды будут формулы объема и их доказательства для конуса и усеченного конуса.

Теорема (формула объема конуса)

Объем конуса равен трети произведения площади основания на высоту:

где 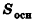— площадь основания конуса, R — радиус, h — высота.

Следствие (формула объема усеченного конуса)

Объем усеченного конуса вычисляется по формуле

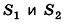
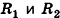
где h – высота усеченного конуса, – площади его оснований, – радиусы его оснований.

С помощью вписанных и описанных призм мы вывели формулу для объема цилиндра. Подобную связь можно установить также для конусов и пирамид.

Определение:

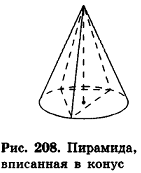
Пирамида называется вписанной в конус, если их вершины совпадают, а основание пирамиды вписано в основание конуса.

При этом конус называется описанным около пирамиды.

Очевидно, что высоты пирамиды и описанного конуса равны, а боковые ребра пирамиды являются образующими конуса (рис. 208).

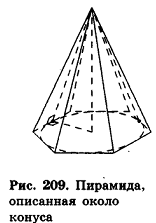
Определение:

Пирамида называется описанной около конуса, если их вершины совпадают, а основание пирамиды описано около основания конуса.

При этом конус называется вписанным в пирамиду.

Очевидно, что высоты пирамиды и вписанного конуса равны, а высоты боковых граней пирамиды являются образующими конуса (рис. 209).

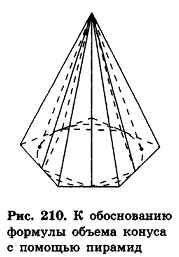
Рассмотрим правильные л-угольные пирамиды, вписанные в данный конус, и правильные л-угольные пирамиды, описанные около него (рис. 210).

Если число n сторон оснований этих пирамид неограниченно возрастает, то площади их оснований стремятся к площади круга, лежащего в основании конуса. Следовательно, их объемы стремятся 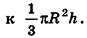Тогда существуют вписанные в конус и описанные около него пирамиды с объемами, сколь угодно мало отличающимися от

Из этих рассуждений становится понятным другое обоснование формулы объема конуса

Объем шара и его частей

Непосредственно получить только из геометрических рассуждений формулу для объема шара очень сложно. Но с помощью интегральной формулы объема и принципа Кавальери доказательство соответствующих результатов является простым и наглядным.

Теорема (формула объема шара)

Объем шара радиуса R вычисляется по формуле

Доказательство:

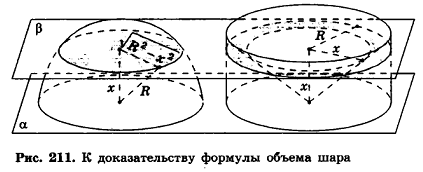
Найдем сначала объем полушара, применив принцип Кавальери.

Пусть дан полушар F_l радиуса R. На плоскость а, содержащую основание полушара, поставим цилиндр, радиус и высота которого также равны R. В цилиндр впишем конус, вершина которого совпадает с центром основания цилиндра в плоскости а, а основание — с другим основанием цилиндра (рис. 211).

Сравним объем V₁ полушара с объемом V₂ тела F₂, ограниченного нижним основанием цилиндра и боковыми поверхностями цилиндра и конуса.

Проведем плоскость , параллельную плоскости а и удаленную от нее на расстояние х . Эта плоскость пересечет данный полушар по кругу радиуса и площади , а тело F₂ — по кольцу. Так как осевое сечение конуса является равнобедренным прямоугольным треугольником, внешний радиус кольца равен R, а внутренний — х. Значит, площадь полученного кольца составит и будет равна площади сечения полушара. По принципу Кавальери, объем полушара равен объему тела F₂, то есть разности объемов цилиндра и конуса:

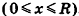
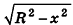
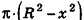
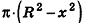
Объем шара вдвое больше объема полушара, следовательно, вычисляется по формуле 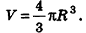. Теорема доказана.

Пример №4

Сечение шара, удаленное от его центра на 1 см, имеет площадь 8л см². Найдите объем шара.

Решение:

Пусть дан шар с центром О. Сечение шара некоторой плоскостью а является кругом с центром , причем . Так как О удалена от а на 1 см, то = 1 см.

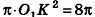
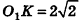
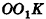
Пусть точка К сферы, ограничивающей шар, принадлежит данному сечению (рис. 212). Тогда площадь сечения равна , откуда (см). Из прямоугольного треугольника по теореме Пифагора имеем:

По формуле объема шара

Ответ:

Найдем теперь объемы частей шара.

Определение:

Шаровым сегментом называется часть шара, отсекаемая от него некоторой плоскостью.

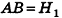
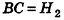
На рисунке 213 плоскость сечения, проходящая через точку В, разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется основанием этих сегментов, а длины отрезков диаметра, перпендикулярного плоскости сечения,— высотами сегментов. Так, на рисунке 213 — высота меньшего сегмента, — высота большего сегмента.

Теорема (формула объема шарового сегмента)

Объем шарового сегмента вычисляется по формуле

где R — радиус шара, Н — высота сегмента.

Доказательство:

Применим для шарового сегмента интегральную формулу объема.

Введем декартову систему координат так, чтобы ее начало совпадало с центром шара.

Тогда часть шара, ограниченная плоскостями 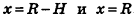, является шаровым сегментом с высотой Н (рис. 214).

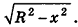
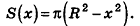
Радиус сечения шарового сегмента плоскостью, пересекающей ось Ох в точке (х;0;0), равен Следовательно, площадь этого сечения По интегральной формуле объема для шарового сегмента получаем:

Теорема доказана.

Заметим, что при Н -2R из только что доказанной формулы следует еще один способ нахождения формулы объема шара:

Определение:

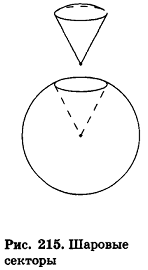
Шаровым сектором называется тело, ограниченное сферической поверхностью шарового сегмента и боковой поверхностью конуса, основанием которого является основание сегмента, а вершиной – центр шара.

Очевидно, что если шаровой сегмент меньше полушара, его дополняют конусом для получения шарового сектора; если же шаровой сегмент больше полушара, то для получения шарового сектора конус из него удаляют (рис. 215).

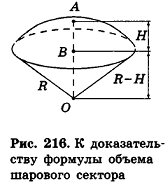
Теорема (формула объема шарового сектора)

Объем шарового сектора вычисляется по формуле

где R — радиус шара, Я — высота соответствующего шарового сегмента.

Доказательство:

Рассмотрим случай шарового сектора, высота Я соответствующего шарового сегмента для которого меньше R (рис. 216).

Тогда его объем равен сумме объема сегмента 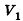и объема конуса V₂. Следовательно,

Случай, когда высота Н больше или равна R, рассмотрите самостоятельно.

Теорема доказана.

Определение:

Шаровым слоем (поясом) называется часть шара, заключенная между двумя параллельными секущими плоскостями.

Расстояние между этими плоскостями называется высотой шарового слоя, а сечения, ограничивающие слой,— основаниями шарового слоя (рис. 217).

Заметим, что объем шарового слоя можно вычислить двумя способами:

1. как разность объемов двух шаровых сегментов;
2. как разность объема шара и объемов двух сегментов, не входящих в слой.

Объемы подобных тел

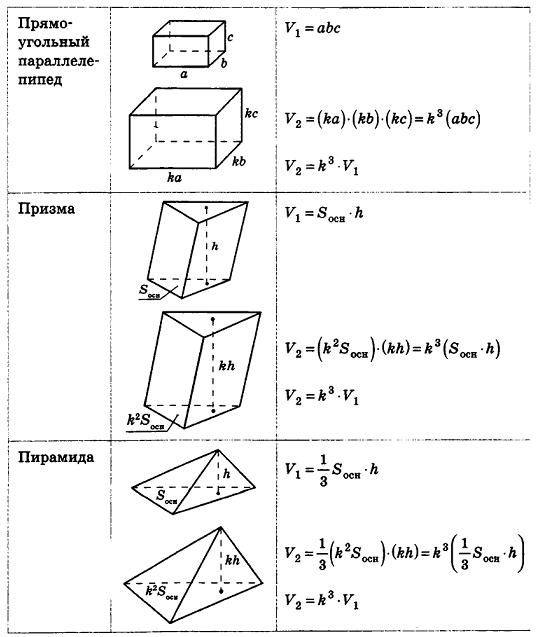
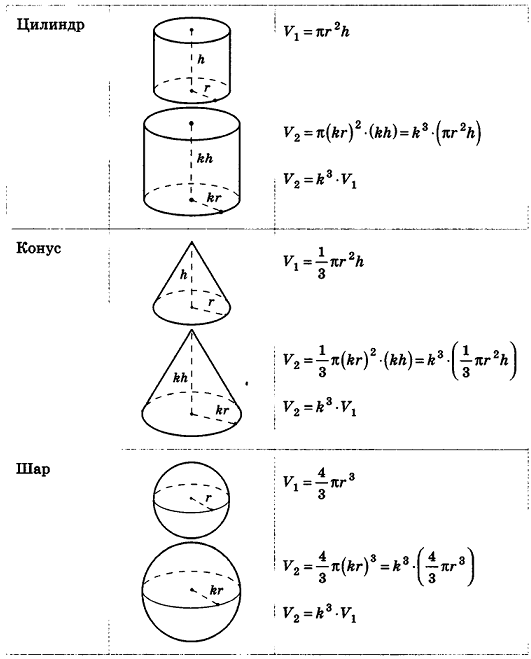
Из повседневного опыта нам хорошо известно, что при увеличении размеров предмета его объем также увеличивается. Например, легко сравнить объемы двух аквариумов, размеры одного из которых вдвое меньше соответствующих размеров другого (рис. 218): объемы отличаются в 8 раз.

Кроме того, можно проследить за подобными с коэффициентом k многоугольниками на плоскости. Как известно, их периметры отличаются в k раз, площади — в k² раз. Естественно предположить, что объемы подобных с коэффициентом k пространственных тел отличаются к³ раз. Проверим это для тел, формулы объема которых нам уже известны.

Итак, для всех рассмотренных тел верно следующее утверждение: объемы тел, подобных с коэффициентом k, относятся как k³.

Этот факт верен и для любых простых тел, то есть тел, которые можно разбить на конечное число треугольных пирамид. В частности, любые многогранники, подобные с коэффициентом к, имеют объемы, которые отличаются в k³ раз.

Пример №5

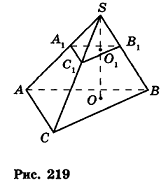
Через середину высоты пирамиды проведена плоскость, параллельная основанию. В каком отношении она делит объем пирамиды?

Решение:

Пусть дана пирамида с вершиной S и высотой SO. Плоскость, параллельная основанию пирамиды, пересекает SO в точке 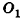(рис. 219).

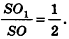
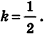
По условию = Но отсекаемая пирамида подобна данной, причем отношение их высот равно коэффициенту подобия, то есть По свойству объемов подобных тел объем отсекаемой пирамиды в 8 раз меньше объема данной пирамиды. Следовательно, данная плоскость, параллельная основанию пирамиды, делит ее объем в отношении 1:7.

Ответ: 1:7.

Была ли эта статья полезной?

Вычисление объема тела

Вычисление объема тела по известным площадям параллельных сечений

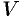
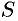
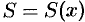
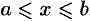
Пусть требуется найти объем тела, причем известны площади сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси : , .

Применим схему II (метод дифференциапа).

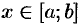
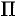
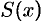
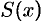
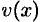
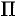
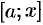
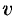
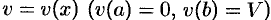
1. Через произвольную точку проведем плоскость , перпендикулярную оси (см. рис. 187). Обозначим через площадь сечения тела этой плоскостью; считаем известной и непрерывно изменяющейся при изменении . Через обозначим объем части тела, лежащее левее плоскости . Будем считать, что на отрезке величина есть функция от , т. е. .

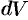
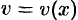
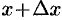
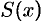
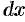
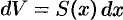
2. Находим дифференциал функции . Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось в точках и , который приближенно может быть принят за цилиндр с основанием и высотой . Поэтому дифференциал объема .

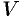
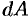
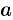
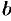
3. Находим искомую величину путем интегрирования в пределах от до :

Полученная формула называется формулой объема тела по площади параллельных сечений.

Пример №41.6.

Найти объем эллипсоида .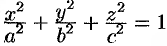

Решение:

Рассекая эллипсоид плоскостью, параллельной плоскости и на расстоянии от нее , получим эллипс (см. рис. 188):

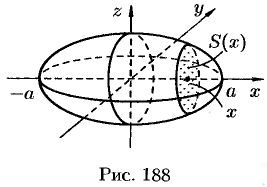
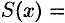
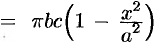
Площадь этого эллипса равна . Поэтому, по формуле (41.6), имеем

Объем тела вращения

Пусть вокруг оси вращается криволинейная трапеция, ограниченная непрерывной линией , отрезком и прямыми и (см. рис. 189). Полученная от вращения фигура, называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси , проведенной через произвольную точку оси (), есть круг с радиусом . Следовательно, .

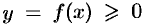
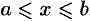
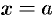
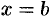
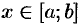
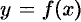
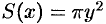
Применяя формулу (41.6) объема тела по площади параллельных сечений, получаем

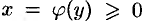
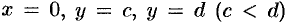
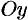
Если криволинейная трапеция ограничена графиком непрерывной функции и прямыми , то объем тела, образованною вращением этой трапеции вокруг оси , по аналогии с формулой (41.7), равен

Пример №41.7.

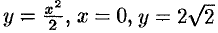
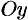
Найти объем тела, образованною вращением фигуры, ограниченной линиями вокруг оси (см. рис. 190).

Решение:

По формуле (41.8) находим:

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

• Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны: