
{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
Формула объема прямоугольного параллелепипеда через три стороны
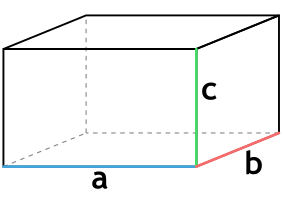
{V= a cdot b cdot c}
a – длина параллелепипеда
b – ширина параллелепипеда
c – высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab – это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
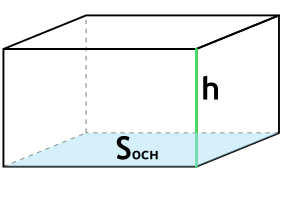
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
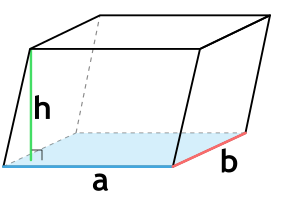
{V= a cdot b cdot h}
a – длина основания параллелепипеда
b – ширина основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через площадь основания и высоту
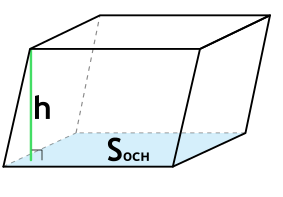
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
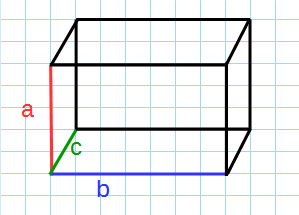
Формула объема параллелепипеда через его ребра:
a,b,c – ребра параллелепипеда.
Через стороны и высоту
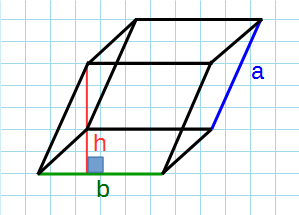
Формула объема параллелепипеда:
a,b – ребра параллелепипеда; h – высота параллелепипеда.
Калькулятор объема параллелепипеда
Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
Что известно
Размерность
Длина
см
Ширина
см
Площадь основания
см2
Высота
см
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🧑🏾💻 Что считает калькулятор
Калькулятор объема параллелепипеда – это инструмент, который позволяет вычислять объем любого параллелепипеда и выводить результат в разных единицах измерения.
📦 Как использовать калькулятор
Укажите значение сторон для прямоугольного параллелепипеда или сторон и высоты для наклонного, после этого калькулятор произведет расчёт и выдаст его в указанных единицах измерения.
📐 Что влияет на точность расчетов калькулятора
Точность расчетов калькулятора объема параллелепипеда зависит от нескольких факторов:
- Корректность ввода данных. Если вводимые значения длины, ширины и высоты параллелепипеда некорректны, то расчет объема будет неправильным. Поэтому, важно убедиться в правильности вводимых значений перед выполнением расчета.
- Точность математических операций. Расчет объема параллелепипеда требует выполнения математических операций, таких как умножение. Если калькулятор не выполняет математические операции точно, то результаты расчетов будут неточными.
- Точность округления. в некоторых случаях, результаты расчетов могут быть округлены. Если калькулятор округляет результаты до неправильного числа знаков, то результаты будут неточными.
- Алгоритм расчета. Различные калькуляторы могут использовать разные алгоритмы расчета. Если алгоритм расчета неправильный, то результаты могут быть неточными.
- Ошибки программирования. Если в программе калькулятора есть ошибки, то результаты расчетов могут быть неправильными. Поэтому, важно использовать калькуляторы, которые были разработаны и протестированы надежными разработчиками.
🗂️ Где можно применить калькулятор
Калькулятор объема параллелепипеда может быть использован во многих областях, где требуется расчет объема параллелепипеда. Некоторые из таких областей включают:
- Строительство. Калькулятор объема параллелепипеда может использоваться строителями при расчете объема блоков в форме параллелепипеда, бетонных блоков, кирпичей и других материалов, используемых в строительстве.
- Производство. Калькулятор объема параллелепипеда может использоваться в производственных процессах для расчета объема материалов, таких как металл, пластик, стекло и другие, используемых в производстве изделий.
- Логистика. Калькулятор объема параллелепипеда может использоваться при планировании грузоперевозок, чтобы определить, сколько грузовых мест может вместить транспортное средство.
- Образование. Калькулятор объема параллелепипеда может использоваться учителями математики в школах и университетах для обучения геометрии и расчета объема.
- Интерьер и дизайн. Калькулятор объема параллелепипеда может использоваться в дизайне интерьера для расчета объема элементов в форме параллелепипеда, таких как шкафы, полки, столы и другие.
- Ремонт и обслуживание. Калькулятор объема параллелепипеда может использоваться в ремонте и обслуживании, чтобы определить количество материалов, необходимых для замены элементов, таких как плитка, обои и другие.
🤔 Как вычислить объем параллелепипеда самостоятельно
Объем параллелепипеда можно вычислить самостоятельно, используя формулу:
V = a * b * h
где a, b, и h – это соответственно длины трех сторон параллелепипеда.
Шаги для вычисления объема параллелепипеда:
- Измерьте длину одной из сторон параллелепипеда и запишите ее значение. Обозначим ее как “a”.
- Измерьте длину второй стороны и запишите ее значение. Обозначим ее как “b”.
- Измерьте высоту параллелепипеда и запишите ее значение. Обозначим ее как “h”.
- Умножьте значение “a” на значение “b”.
- Умножьте результат из шага 4 на значение “h”.
- Полученный результат будет объемом параллелепипеда.
Например, если длина первой стороны равна 3 см, длина второй стороны равна 4 см, а высота равна 5 см, то объем параллелепипеда будет:
V = 3 см * 4 см * 5 см = 60 куб. см
🤓 Полезные советы
Несколько советов, которые могут помочь при вычислении объема параллелепипеда:
- Определите тип параллелепипеда: правильный, прямоугольный или наклонный. Это позволит выбрать правильную формулу для расчета объема.
- Измерьте длину, ширину и высоту параллелепипеда в соответствующих единицах измерения. Обычно используются метры, сантиметры или дюймы.
- Убедитесь, что все измерения были взяты в одной системе измерения. Если это не так, преобразуйте измерения в одну систему измерения.
- Примените правильную формулу для расчета объема, в зависимости от типа параллелепипеда. Для правильного параллелепипеда объем равен длине ребра в кубе. Для прямоугольного параллелепипеда объем равен произведению длины, ширины и высоты. Для наклонного параллелепипеда объем равен площади основания, умноженной на высоту.
- Проверьте свои вычисления, чтобы избежать ошибок. Дважды проверьте формулу и убедитесь, что все измерения были взяты правильно.
- Используйте калькулятор или компьютерную программу для автоматического расчета объема. Это может сократить время и снизить вероятность ошибок.
- Округляйте результат до нужного количества знаков после запятой, в зависимости от требований задачи.
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемые вопросы про вычисление объема параллелепипеда.
Что такое параллелепипед и как он выглядит?
Параллелепипед – это геометрическое тело, имеющее шесть прямоугольных граней. Он выглядит как прямоугольный блок с равными гранями и прямыми углами между ними.
Как рассчитать объем параллелепипеда?
Объем параллелепипеда можно вычислить, умножив длину, ширину и высоту параллелепипеда. Формула для расчета объема V = l * w * h, где V – объем, l – длина, w – ширина и h – высота параллелепипеда.
Как измерить длину, ширину и высоту параллелепипеда?
Для измерения длины, ширины и высоты параллелепипеда необходимо использовать линейку или мерную ленту. Длину измеряют вдоль одной из его граней, ширину – вдоль другой грани, а высоту – перпендикулярно этим граням.
Как связаны площадь основания и высота с объемом параллелепипеда?
Объем параллелепипеда зависит от площади его основания и высоты. Чем больше площадь основания и высота параллелепипеда, тем больше будет его объем.
В каких единицах измеряется объем параллелепипеда?
Объем параллелепипеда измеряется в кубических единицах длины, таких как кубические метры, кубические сантиметры, кубические дюймы и т. д.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
- Калькулятор площади трапеции. Рассчитайте онлайн площадь трапеции, не только зная длины ее оснований и высоту, но и по другим известным параметрам, например, диагоналям.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
В данной публикации мы рассмотрим, как можно найти объем параллелепипеда и разберем примеры решения задач для закрепления материала.
-
Формула вычисления объема параллелепипеда
- 1. Общая формула
- 2. Объем прямоугольного параллелепипеда
-
Примеры задач
Формула вычисления объема параллелепипеда
1. Общая формула
Объем любого параллелепипеда равняется произведению площади его основания на высоту.
V = Sосн ⋅ h

- Sосн – площадь основания (ABCD или EFHG, равны между собой);
- h – высота.
Данная формула справедлива для всех видов геометрической фигуры:
- наклонной – боковые грани не перпендикулярны основаниям;
- прямой – все боковые грани (4 шт.) являются прямоугольниками;
- прямоугольной – все грани (боковые и основания) являются прямоугольниками;
- ромбоэдра – все грани являются равными ромбами;
- куба – все грани представляют собой равные квадраты.
2. Объем прямоугольного параллелепипеда
Объем фигуры равен произведению его длины на ширину на высоту.
V = a ⋅ b ⋅ c

Формула следует из следующих утверждений:
- Основанием фигуры является прямоугольник, площадь которого считается как произведение его длины (a) на ширину (b).
- Высота фигуры – это длина боковой грани (c).
Примеры задач
Задание 1
Найдите объем параллелепипеда, если известно, что площадь его основания равняется 20 см2, а высота – 7 см.
Решение:
Используем первую формулу, подставив в нее известные нам значения:
V = 20 см2 ⋅ 7 см = 140 см3.
Задание 2
Дан прямоугольный параллелепипед. Длина и ширина его основания равны 9 см и 5 см, соответственно, а высота составляет 6 см. Найдите объем фигуры.
Решение:
Воспользуемся формулой для данного типа фигуры:
V = 9 см ⋅ 5 см ⋅ 6 см = 270 см3.
Параллелепипед — это призма, основанием которой является параллелограмм.
Онлайн-калькулятор объема параллелепипеда
Как и у куба, у этого многогранного тела есть двенадцать ребер, шесть граней и восемь вершин. Вид параллелепипеда зависит от геометрической фигуры, лежащей в основании, и от угла, образованного им при пересечении с гранями.
Если его гранями являются прямоугольники, то он называется прямоугольным.
Если такие прямоугольники имеют отношение только к боковым граням, то он называется прямым.
Иногда бывают случаи, когда эти грани образуют не прямой угол с основанием. Тогда в данном случае параллелепипед является наклонным.
Если он состоит исключительно из равных ромбов, то он называется ромбоэдром.
Если все грани параллелепипеда являются одинаковыми квадратами, то получаем куб. Таким образом, куб — это частный случай параллелепипеда.
Формула объема прямоугольного параллелепипеда
Объемом такого параллелепипеда называется произведение всех его трех измерений: длины, ширины, высоты. Вычисляется он так:
V=a⋅b⋅cV=acdot bcdot c
a,b,ca, b, c — длина, ширина и высота прямоугольного параллелепипеда.
Рассмотрим несколько примеров.
Найти объем прямоугольного параллелепипеда, если известны его длина, равная 5 см.5text{ см.}, ширина, имеющая длину 10 см.10text{ см.} и высота длиной в 7 см.7text{ см.}
Решение
a=5a=5
b=10b=10
c=7c=7
Сразу подставляем в формулу численные значения:
V=a⋅b⋅c=5⋅10⋅7=350 см3V=acdot bcdot c=5cdot 10cdot 7=350text{ см}^3
Ответ
350 см3.350text{ см}^3.
Формула объема наклонного параллелепипеда
V=Sосн⋅hV=S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания наклонного параллелепипеда;
hh — его высота.
Вычислить объем наклонного параллелепипеда, если в его основании лежит прямоугольник со сторонами в 4 см.4text{ см.} и 5 см.5text{ см.}, а высота его равна 10 см.10text{ см.}
Решение
a=4a=4
b=5b=5
h=10h=10
Находим площадь основания, то есть площадь прямоугольника:
Sосн=a⋅b=4⋅5=20S_{text{осн}}=acdot b=4cdot 5=20
Сам объем равен:
V=Sосн⋅h=20⋅10=200 см3V=S_{text{осн}}cdot h=20cdot 10=200text{ см}^3
Ответ
200 см3.200text{ см}^3.
Формула объема параллелепипеда через определитель
Альтернативным способом нахождения объема параллелепипеда является вычисление смешанного произведения векторов, на которых построен данный параллелепипед.
Пусть параллелепипед построен на векторах a⃗vec{a}, b⃗vec{b} и c⃗vec{c} с координатами:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующего параллелепипеда это определитель, составленный из этих координат:
V=∣axayazbxbybzcxcycz∣V=begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем параллелепипеда через смешанное произведение векторов, координаты которых таковы: a⃗=(2,3,5)vec{a}=(2, 3, 5), b⃗=(1,4,4)vec{b}=(1, 4, 4), c⃗=(3,5,7)vec{c}=(3, 5, 7).
Решение
a⃗=(2,3,5)vec{a}=(2, 3, 5)
b⃗=(1,4,4)vec{b}=(1, 4, 4)
c⃗=(3,5,7)vec{c}=(3, 5, 7)
По формуле:
V=∣235144357∣=2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7=56+36+25−60−40−21=−4V=begin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 – 5cdot4cdot3 – 2cdot4cdot5 – 3cdot1cdot7 = 56 + 36 + 25 – 60 – 40 – 21 = -4
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=4 см3V=4text{ см}^3
Ответ
4 см3.4text{ см}^3.
У вас не получается решить задачу по геометрии? Наши эксперты помогут вам!
