Объем прямоугольника

4.6
Средняя оценка: 4.6
Всего получено оценок: 107.
4.6
Средняя оценка: 4.6
Всего получено оценок: 107.
В этой статье мы поговорим о разности определений объема и площади, а так же о прямоугольнике и параллелепипеде. Разделим все понятия, обсудим, как найти площадь и как определить объем.
Определения
Часто в жизни люди совершают математические ошибки. Причем зачастую не в силу какого-то грубого незнания, а просто из-за громоздкости названий. Это не совсем верно, поскольку ведет к увеличению числа ошибок.
Формулы объема прямоугольника не существует.
Фигура может быть:
- одномерной, то есть представлять собой точку или прямую
- двумерной, то есть быть составленной из точек или прямых в плоскости
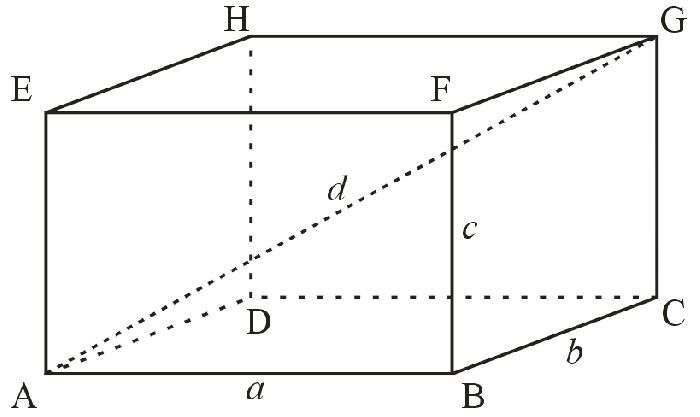
- трехмерной, то есть воплощенной в пространстве. Трехмерные фигуры это то, что нас окружает. Арбуз идеальной формы – это пример шара, а пятирублевая монетка – круга; коробка здания представляет собой параллелепипед, колпаки волшебников из книг – конусы. Пространственная геометрия повсюду. Но если листовка с рекламой, это прямоугольник, то коробка – параллелепипед.
Разделение определений поможет избежать ошибок.
Двумерная фигура характеризуется периметром и площадью. Трехмерная имеет периметр, площадь поверхности и объем. Как понять, есть ли объем у фигуры? Достаточно представить себе, что засыпаешь в нее песок. Задержится ли он в фигуре?
В трехмерной: конусе, цилиндре, параллелепипеде – песок останется лежать, заполняя собой внутренне пространство (то есть объем). В двумерной песок просто насыплется сверху. Разделочную доску нельзя заполнить песком, так же как и нельзя найти объем прямоугольника.
Объем и площадь
Объем это пространственная характеристика. Она показывает, сколько место фигура занимает в пространстве или сколько нужно сыпучего материала или воды, чтобы заполнить фигуру изнутри.
Площадь это двумерная характеристика. Она показывает, к примеру, сколько места займет фигура на столе. Если нам нужно понять, сколько места занимает лист на столе, то считаем площадь, для того, что понять вместится ли учебник в ящик стола, нужно посчитать объем.
Из двумерных прямоугольников составляют трехмерную фигуру, которую называют прямоугольным параллелепипедом. Прямоугольный параллелепипед состоит из шести прямоугольников, которые называют гранями. Четыре боковых грани равны между собой, так же как равны между собой две оставшиеся грани-основания.
Чтобы найти площадь прямоугольника нужно перемножить между собой две стороны, выходящие из одной точки, то есть смежные. Для того, чтобы найти площадь поверхности прямоугольного параллелепипеда нужно сложить площади всех его граней.
Удивительно, но понятие объема появилось еще в Древней Греции. Им оперировал Евклид, Аристотель и Архимед. Но определение было размытым и неточным. Древние ученые увлекались двумерным пространством. Точное определение объема было дано лишь в 19 веке учеными Пеано и Жорданом.
Чтобы найти объем прямоугольного параллелепипеда, нужно так же перемножить между собой стороны, выходящие из одной точки. Но в пространстве их будет три: длина, ширина и высота.
Что мы узнали?
Мы разделили понятия фигур по пространственным характеристикам. Узнали как создается прямоугольный параллелепипед и разделили параллелепипед и прямоугольник, поговорили о расчете площади и объема. Привели примеры геометрических фигур из реальной жизни. Узнали, что объема прямоугольника не существует.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Ксения Кузнецова
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 107.
А какая ваша оценка?
Калькулятор для расчета объема параллелепипеда
C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер “a”, “b”, “c” и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку “Рассчитать”
Округлить результат до
знаков после запятой
Рассчитать
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
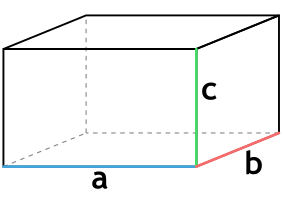
где a, b, c – ребра параллелепипеда.

{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
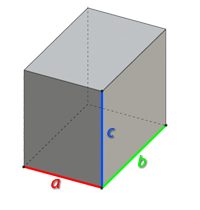
Формула объема прямоугольного параллелепипеда через три стороны
{V= a cdot b cdot c}
a – длина параллелепипеда
b – ширина параллелепипеда
c – высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab – это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
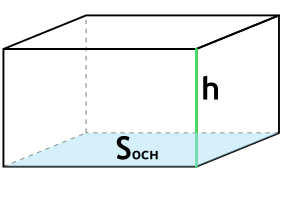
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
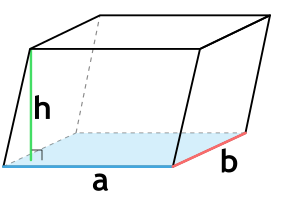
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
{V= a cdot b cdot h}
a – длина основания параллелепипеда
b – ширина основания параллелепипеда
h – высота параллелепипеда
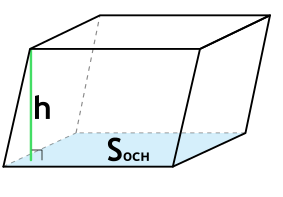
Формула объема наклонного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Введите а — длину прямоугольника в м (метрах):
Введите b — ширину прямоугольника в м (метрах):
Введите h — толщину прямоугольника в м (метрах):
Как рассчитать объем прямоугольника?
Если прямоугольник имеет толщину, то фактически это параллелепипед. Объем параллелепипед в общем случае рассчитывается по формуле:
V = a x b х h
V — объем параллелепипеда . Объем прямоугольника имеющего толщину (высоту).
a — длина прямоугольника основания параллелепипеда
b — ширина прямоугольника основания параллелепипеда
h — высота параллелепипеда. Толщина прямоугольника.
Объем в миллиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vмм3 = aм х bм х hм x 1 000 000 000
Vмм3 — объем в миллиметрах кубических (мм3).
aм — длина прямоугольника в метрах (м).
bм — ширина прямоугольника в метрах (м).
hм — толщина прямоугольника в метрах (м).
Объем в сантиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vсм3 = aм х bм х hм x 1 000 000
Vсм3 — объем в сантиметрах кубических (см3).
aм — длина прямоугольника в метрах (м).
bм — ширина прямоугольника в метрах (м).
hм — толщина прямоугольника в метрах (м).
Объем в метрах кубических прямоугольника имеющего толщину (параллелепипед):
Vм3 = aм х bм х hм
Vм3 — объем в метрах кубических (м3).
aм — длина прямоугольника в метрах (м).
bм — ширина прямоугольника в метрах (м).
hм — толщина прямоугольника в метрах (м).
Объем в литрах прямоугольника имеющего толщину (параллелепипед):
Vл = aм х bм х hм x 1 000
Vл — объем в литрах (л).
aм — длина прямоугольника в метрах (м).
bм — ширина прямоугольника в метрах (м).
hм — толщина прямоугольника в метрах (м).
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
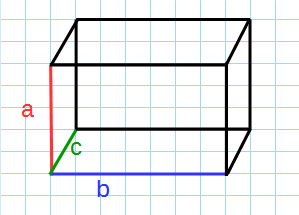
Формула объема параллелепипеда через его ребра:
a,b,c – ребра параллелепипеда.
Через стороны и высоту
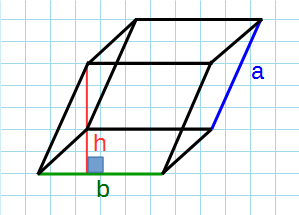
Формула объема параллелепипеда:
a,b – ребра параллелепипеда; h – высота параллелепипеда.