{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
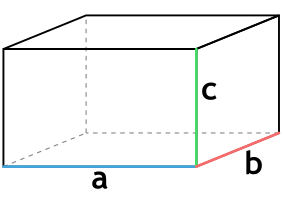
Формула объема прямоугольного параллелепипеда через три стороны
{V= a cdot b cdot c}
a – длина параллелепипеда
b – ширина параллелепипеда
c – высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab – это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
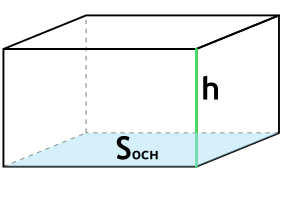
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
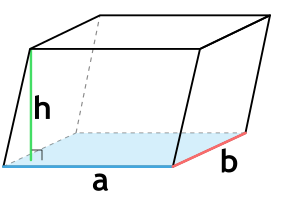
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
{V= a cdot b cdot h}
a – длина основания параллелепипеда
b – ширина основания параллелепипеда
h – высота параллелепипеда
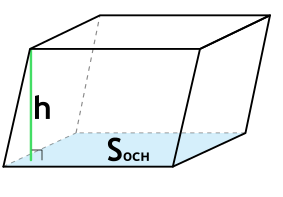
Формула объема наклонного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Сегодня Бим, Бом и ребята изучают объем геометрических фигур, геометрическую фигуру — прямоугольный параллелепипед, а также как найти объем прямоугольного параллелепипеда, и какие существуют единицы измерения объема.
Содержание статьи:
Объем геометрических фигур
Определение. Объем — это сколько места занимает фигура в пространстве.
Сегодня в цирке выходной. Бом прогуливает своих питомцев в парке, Бим помогает Бому.
— Вот я перед прогулкой зашел в магазин “Товары для животных” и купил специальные конфеты для твоих обезьянок, — обрадовал друга Бим. — Посмотри в какой объемной упаковке конфеты! Здесь можно измерить и длину, и ширину, и высоту коробки. А ведь раньше мы измеряли только длину и ширину донышка коробки.
— А ну-ка дай посмотреть! — попросил Бом. — Какая интересная коробка! Смотри, ее можно раскрыть с разных сторон.
— Ну да, — ответил Бим. — Ты только осторожнее, старайся открыть так, чтобы конфеты можно было вынуть только сверху. А то вдруг они разлетятся по всему парку! Попробуй тогда найди их все, да еще ведь и непонятно, сколько их там!
— Да, раньше мы рассматривали только плоские фигуры, — задумался Бом. — А у этой коробки могут быть три разных донышка, смотря с какой стороны ее открывать. И что же тогда в ней донышком называть? И как считать, сколько конфет в нее может поместиться? Вот если у донышка есть длина и ширина, но коробочка еще и высокая, то получается, что у нее и высота есть?
— Смотри, вон гуляют Коля, Вася и Оля! Может они нам объяснят?
Ребята тоже увидали Бима и Бома, да еще и с обезьянками. Как тут не подойти! Все радостно поздоровались друг с другом.
— Ой, какие обезьянки! — закричали дети.
Оля достала из сумочки банан:
— Можно угостить обезьянок? — спросила девочка.
— Конечно можно, — ответил Бом.
— Ой, у тебя, Оля, сумочка похожа на вот эту коробочку, у нее есть донышко, но она высокая. Значит, у сумочки тоже есть длина, ширина и высота. — удивился Бим. — Как же такие фигуры называются?
— Такие фигуры называются объемными, — ответил Вася. — Мы видим предметы вокруг нас: деревья, людей, машины, сумки, животных и еще очень много других предметов и у всех у них есть длина, ширина и высота.
— Люди договорились между собой, что такие предметы называются объемными, — добавил Коля, — и ввели понятие объема, то есть, сколько места занимает фигура в пространстве. Также решили, как измерять объем, — и ввели единицы измерения объема.
Объем прямоугольного параллелепипеда
Прямоугольный параллелепипед
Определение. Прямоугольный параллелепипед — это геометрическая фигура, имеющая внизу и вверху два одинаковых прямоугольника, у которых соответствующие вершины соединены отрезками, перпендикулярными к сторонам этих прямоугольников.
Объяснение продолжила Оля:
— Проще всего вычислить объем прямоугольного параллелепипеда. Прямоугольный параллелепипед — это геометрическая фигура, у которой внизу и вверху два одинаковых прямоугольника, соответствующие вершины прямоугольников соединяются отрезками. Эти отрезки перпендикулярны сторонам прямоугольников в верхнем и нижнем основаниях. Таких точек 8: 4 снизу и 4 сверху. В каждой такой точке получается 3 прямых угла и 3 отрезка.
Вот, посмотрите: на коробке тоже всего таких точек 8, из них 4 снизу на донышке и 4 сверху на крышечке. Эти 8 точек называют вершинами параллелепипеда. 12 линий (4 вверху, 4 внизу и 4 по бокам), которые соединяют вершины параллелепипеда называют ребрами, ребра образуют 6 прямоугольников (2 основания — донышко и крышечка, и 4 боковые стороны), которые называются гранями параллелепипеда.
Находим объем прямоугольного параллелепипеда
Правило. Для вычисления объема прямоугольного параллелепипеда надо длину основания умножить на ширину основания и умножить на высоту параллелепипеда.
Дальше объяснял Вася:
— Для того чтобы вычислить объем прямоугольного параллелепипеда, надо измерить длину двух прилегающих сторон прямоугольников (a, b) в основании и измерить длину ребра соединяющего нижнее и верхнее основания — это высота параллелепипеда (h). И потом перемножить длину этих сторон.
V = a × b × h (куб. ед. дл.).
— Давайте измерим объем вашей коробки и объем Олиной сумки, — предложил Коля.
Мальчик достал из портфеля угольник и начал прикладывать его по очереди к каждому углу коробки:
— Видно, что все углы прямые, — сделал вывод Коля. — Значит у нас прямоугольный параллелепипед. Длина и ширина сторон основания 5 см и 4 см:
a = 5 см, b = 4 см.
Высота параллелепипеда, то есть, длина отрезка, соединяющего верхнее и нижнее основания, — равна 6 см:
h = 6 см.
Значит, объем параллелепипеда равен
V = a × b × h, V = 5 × 4 × 6 = 120 (куб. см).
— Теперь измерим объем моей сумки-портфеля, — продолжила Оля. — Смотрим: все углы прямые, значит — можем воспользоваться формулой для объема прямоугольного параллелепипеда. Здесь у нас:
длина 30 см = 3 дм, ширина 20 см = 2 дм, высота 40 см = 4 дм.
Объем равен
V = 3 × 2 × 4 = 24 куб. дм.
Единицы измерения объема.
Единицами измерения объема являются:
1 куб. мм, 1 куб. см, 1 куб. дм, 1 куб. м, 1 куб. км,1 л.
— А в каких еще единицах измеряют объем? — поинтересовался Бим.
— Кроме кубических сантиметров и кубических дециметров, объем измеряют еще в кубических метрах, кубических миллиметрах, кубических километрах и в литрах, — ответил Вася. — Один литр равен объему куба (прямоугольный параллелепипед, у которого все стороны одинаковые) со стороной в 1 дм.
1 л = 1 куб. дм.
Кстати, Оля! Получается, что объем твоей сумки равен 24 л.
— При вычислении объема все три измерения — длина, ширина и высота, — должны быть записаны в одинаковых единицах измерения длины: или в миллиметрах, или в сантиметрах, или в дециметрах, или в метрах, или в километрах, — заметил Коля. Затем применяют формулу вычисления объема прямоугольного параллелепипеда:
V = a × b × h (куб. ед. дл.).
Если надо, то числа раздробляют, а уже после вычисления объем укрупняют. Есть специальные таблицы для перевода одних единиц измерения объема в другие единицы измерения объема.
Таблицы перевода единиц измерения объема
1 куб. см = 1000 куб. мм
1 куб. дм = 1000 куб. см
1 куб. дм = 1000 000 куб. мм
1 куб. дм = 1л
1 куб. м = 1000 000 000 куб. мм
1 куб. м = 1000 000 куб. см
1 куб. м = 1000 куб. дм
1 куб. м = 1000 л
1 куб. км = 1018 куб. мм
1 куб. км = 1015 куб. см
1 куб. км = 1012 куб. дм
1 куб. км = 109 куб. м
— Давайте теперь запишем для ребят вопросы, — подытожил Бом:
- Что такое объем?
- Что такое прямоугольный параллелепипед?
- Как найти объем прямоугольного параллелепипеда?
- Единицы измерения объема — это?
И ответы:
- Объем — это количество места, которое занимает фигура в пространстве.
- Прямоугольный параллелепипед — это геометрическая фигура, имеющая внизу и вверху два одинаковых прямоугольника, у которых соответствующие вершины соединены отрезками, перпендикулярными к сторонам этих прямоугольников.
- Для вычисления объема прямоугольного параллелепипеда надо длину основания умножить на ширину основания и умножить на высоту параллелепипеда.
- Единицы измерения объема — это:
1 куб. мм, 1 куб.см, 1 куб.дм, 1 куб. м , 1 куб.км,1 л.
Заключение
— Бим, пойдем отведем обезьянок в цирк, — поглядел на часы Бом. — Им пора обедать. Спасибо, ребята! Вы нам с Бимом помогли разобраться, что такое объем, что такое прямоугольный параллелепипед, найти объем прямоугольного параллелепипеда, узнать единицы измерения объема. До встречи в цирке!
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания! Комментарии приветствуются!)))
Объём — количественная характеристика пространства, занимаемого телом или веществом.
Эту характеристику можно измерить с помощью выбранной единицы измерения объёмов.
Единицей измерения объёмов будем считать куб, ребро которого равно единице измерения длины.
В СИ основная единица измерения объёма — кубический метр. Kубический метр — куб, ребро которого равно (1) м. Kубический метр обозначают
м3
.
Применяются также производные от основной единицы измерения: кубический миллиметр, кубический сантиметр, кубический дециметр (литр), кубический километр. Встречаются и внесистемные единицы измерения объёма жидкостей: баррель, пинта, кварта, кубический дюйм.
Рис. (1). Кубик Рубика.
Cвойства объёмов
1. Объём тела есть неотрицательное число.
Рис. (2). Чашка чая.
2. Равные геометрические тела имеют равные объёмы.
Рис. (3). Одинаковые банки.
3. Если геометрическое тело составлено из геометрических тел, не имеющих общих внутренних точек, то объём данного тела равен сумме объёмов составляющих его тел.
Рис. (4). Фигура из кубиков.
Объём прямоугольного параллелепипеда
Призма — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы.
Параллелепипед — призма, основанием которой является параллелограмм.
Прямой параллелепипед — это параллелепипед, у которого (4) боковые грани — прямоугольники.
Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.
Прямоугольный параллелепипед — это прямой параллелепипед, основанием которого является прямоугольник.
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Рис. (5). Прямоугольный параллелепипед.
1. Следствие.
Объём прямоугольного параллелепипеда равен произведению площади основания на высоту.
2. Следствие.
Объём прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту.
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
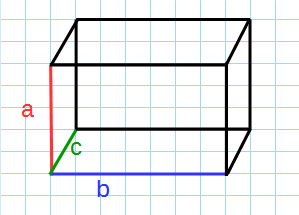
Формула объема параллелепипеда через его ребра:
a,b,c – ребра параллелепипеда.
Через стороны и высоту
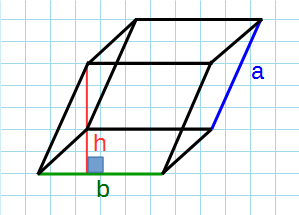
Формула объема параллелепипеда:
a,b – ребра параллелепипеда; h – высота параллелепипеда.
Параллелепипед — это призма, основанием которой является параллелограмм.
Онлайн-калькулятор объема параллелепипеда
Как и у куба, у этого многогранного тела есть двенадцать ребер, шесть граней и восемь вершин. Вид параллелепипеда зависит от геометрической фигуры, лежащей в основании, и от угла, образованного им при пересечении с гранями.
Если его гранями являются прямоугольники, то он называется прямоугольным.
Если такие прямоугольники имеют отношение только к боковым граням, то он называется прямым.
Иногда бывают случаи, когда эти грани образуют не прямой угол с основанием. Тогда в данном случае параллелепипед является наклонным.
Если он состоит исключительно из равных ромбов, то он называется ромбоэдром.
Если все грани параллелепипеда являются одинаковыми квадратами, то получаем куб. Таким образом, куб — это частный случай параллелепипеда.
Формула объема прямоугольного параллелепипеда
Объемом такого параллелепипеда называется произведение всех его трех измерений: длины, ширины, высоты. Вычисляется он так:
V=a⋅b⋅cV=acdot bcdot c
a,b,ca, b, c — длина, ширина и высота прямоугольного параллелепипеда.
Рассмотрим несколько примеров.
Найти объем прямоугольного параллелепипеда, если известны его длина, равная 5 см.5text{ см.}, ширина, имеющая длину 10 см.10text{ см.} и высота длиной в 7 см.7text{ см.}
Решение
a=5a=5
b=10b=10
c=7c=7
Сразу подставляем в формулу численные значения:
V=a⋅b⋅c=5⋅10⋅7=350 см3V=acdot bcdot c=5cdot 10cdot 7=350text{ см}^3
Ответ
350 см3.350text{ см}^3.
Формула объема наклонного параллелепипеда
V=Sосн⋅hV=S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания наклонного параллелепипеда;
hh — его высота.
Вычислить объем наклонного параллелепипеда, если в его основании лежит прямоугольник со сторонами в 4 см.4text{ см.} и 5 см.5text{ см.}, а высота его равна 10 см.10text{ см.}
Решение
a=4a=4
b=5b=5
h=10h=10
Находим площадь основания, то есть площадь прямоугольника:
Sосн=a⋅b=4⋅5=20S_{text{осн}}=acdot b=4cdot 5=20
Сам объем равен:
V=Sосн⋅h=20⋅10=200 см3V=S_{text{осн}}cdot h=20cdot 10=200text{ см}^3
Ответ
200 см3.200text{ см}^3.
Формула объема параллелепипеда через определитель
Альтернативным способом нахождения объема параллелепипеда является вычисление смешанного произведения векторов, на которых построен данный параллелепипед.
Пусть параллелепипед построен на векторах a⃗vec{a}, b⃗vec{b} и c⃗vec{c} с координатами:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующего параллелепипеда это определитель, составленный из этих координат:
V=∣axayazbxbybzcxcycz∣V=begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем параллелепипеда через смешанное произведение векторов, координаты которых таковы: a⃗=(2,3,5)vec{a}=(2, 3, 5), b⃗=(1,4,4)vec{b}=(1, 4, 4), c⃗=(3,5,7)vec{c}=(3, 5, 7).
Решение
a⃗=(2,3,5)vec{a}=(2, 3, 5)
b⃗=(1,4,4)vec{b}=(1, 4, 4)
c⃗=(3,5,7)vec{c}=(3, 5, 7)
По формуле:
V=∣235144357∣=2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7=56+36+25−60−40−21=−4V=begin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 – 5cdot4cdot3 – 2cdot4cdot5 – 3cdot1cdot7 = 56 + 36 + 25 – 60 – 40 – 21 = -4
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=4 см3V=4text{ см}^3
Ответ
4 см3.4text{ см}^3.
У вас не получается решить задачу по геометрии? Наши эксперты помогут вам!