Как найти объем равностороннего цилиндра

Как найти объем равностороннего цилиндра

Здание Планетария Тихо Браге, Копенгаген, его крыша является примером цилиндрического сечения

Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Связанные определения[править | править код]

  • Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей).
  • Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр, называются основаниями этого цилиндра.
  • Часть цилиндрической поверхности, находящаяся между плоскостями оснований, называется боковой поверхностью цилиндра.
  • Высотой цилиндра называется отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка.

Типы цилиндров[править | править код]

  • Прямым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
  • Косым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
  • Круговым называется цилиндр с окружностью в роли направляющей.
  • Цилиндром вращения, или прямым круговым цилиндром (часто под цилиндром подразумевают именно его) называется цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
  • Цилиндр, основания которого являются эллипсами, параболами или гиперболами, называют соответственно эллиптическим, параболическим и гиперболическим; последние два имеют бесконечный объём.
  • Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
  • Равносторонним называется цилиндр вращения, диаметр основания которого равен его высоте[1].

Свойства[править | править код]

  • Если плоскость основания цилиндра параллельна плоскости направляющей, то граница этого основания будет по форме совпадать с направляющей кривой.

Площадь поверхности цилиндра[править | править код]

Площадь боковой поверхности[править | править код]

К вычислению площади боковой поверхности цилиндра

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой h и длиной P, равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

S_{b}=Ph

В частности, для прямого кругового цилиндра:

P=2pi R, и S_{b}=2pi Rh, здесь и далее R — радиус основания цилиндра.

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

S_{b}=P_{perp }h

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма не существует. Для наклонного кругового цилиндра можно воспользоваться приближёнными формулами для периметра эллипса, а затем умножить полученное значение на длину образующей.

Площадь полной поверхности[править | править код]

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:
S_{p}=2pi Rh+2pi R^{2}=2pi R(h+R)

Объём цилиндра[править | править код]

Для наклонного цилиндра существуют две формулы:

  • Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
    V=S_{perp }l,
  • Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания):
    V=Sh=Slsin {varphi },
где l — длина образующей, а varphi  — угол между образующей и плоскостью основания. Для прямого цилиндра h=l.

Для прямого цилиндра sin {varphi }=1, l=h и S_{perp }=S, и объём равен:

  • V=Sl=Sh

Для кругового цилиндра:

V=pi R^{2}h=pi {frac {d^{2}}{4}}h,

где d — диаметр основания.

Примечания[править | править код]

  1. ↑ Математический справочник
Источник

Как рассчитать объем цилиндра

На данной странице калькулятор поможет рассчитать объем цилиндра онлайн. Для расчета задайте высоту, радиус или площадь основания. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

По высоте и радиусу

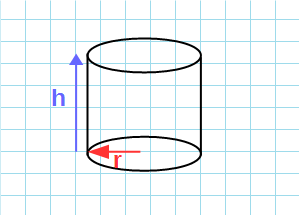
Цилиндр с высотой и радиусом

Формула объема цилиндра через высоту и радиус:

V=π·r²·h

π – константа равная (3.14); r – радиус основания; h – высота цилиндра.

Через площадь основания и высоту

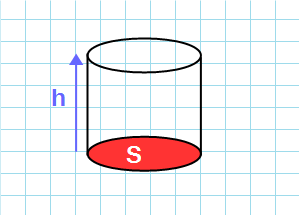
Цилиндр с площадью основания и высотой

Формула объема цилиндра через высоту и площадь основания:

V=S·h

S – площадь основания цилиндра; h – высота цилиндра.

Источник

Объем цилиндра через радиус оснований и высоту

{V= pi R^2 h}

Цилиндр представляет собой простое геометрическое тело, получаемое при вращении прямоугольника вокруг одной из его сторон.

Другое определение: цилиндр – это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.

Рассчитать объем цилиндра можно по нескольким формулам. Для расчета необходимо знать высоту цилиндра и один из параметров – радиус основания, диаметр основания или площадь основания.

Содержание:
  1. калькулятор объема цилиндра
  2. формула объема цилиндра через высоту и радиус
  3. формула объема цилиндра через высоту и площадь основания
  4. формула объема цилиндра через высоту и диаметр
  5. примеры задач

Формула объема цилиндра через высоту и радиус

Объем цилиндра через высоту и радиус

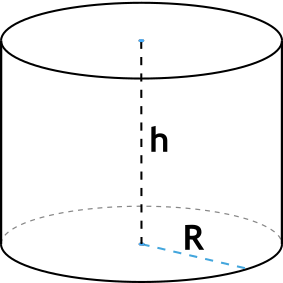
{V= pi R^2 h}

R – радиус основания цилиндра

h – высота цилиндра

Если внимательно посмотреть на эту формулу, то можно заметить, что {pi R^2} – это формула площади круга, а в нашем случае – площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:

Формула объема цилиндра через высоту и площадь основания

Объем цилиндра через высоту и площадь основания

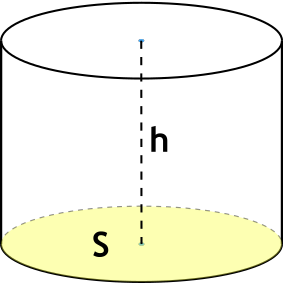
{V= S h}

S – площадь основания цилиндра

h – высота цилиндра

Так как диаметр окружности равен двум радиусам, мы легко можем преобразовать формулу объема цилиндра через радиус и высоту в формулу через диаметр и высоту. Для этого выразим радиус через диаметр и получим необходимую формулу:

D = 2R to R = dfrac{D}{2}

V = pi R^2 h = pi {Big( dfrac{D}{2} Big) }^2 h = pi dfrac{D^2}{4} h

Формула объема цилиндра через высоту и диаметр

Объем цилиндра через высоту и диаметр

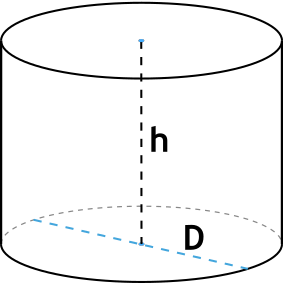
{V= pi {dfrac{D^2}{4}} h}

D – диаметр основания цилиндра

h – высота цилиндра

Примеры задач на нахождение объема цилиндра

Задача 1

Найти объём цилиндра с высотой 3см и диаметром основания 6см.

Решение

Так как в условии задачи нам дан диаметр основания цилиндра, мы будем использовать формулу объема через диаметр. Подставим в нее известные высоту и диаметр, чтобы получить объем цилиндра.

V = pi dfrac{D^2}{4} h = pi dfrac{6^2}{4} 3 = pi dfrac{36}{4} 3 = pi cdot 9 cdot 3 = 27 pi : см^3 approx 84.823 : см^3

Ответ: 27 pi : см^3 approx 84.823 : см^3

Ответ легко проверить с помощью калькулятора .

Задача 2

Найдите объем цилиндра с радиусом основания 5см и высотой 16см.

Решение

Для решения этой задачи воспользуемся формулой объема через радиус.

V = pi R^2 h = pi cdot 5^2 cdot 16 = pi cdot 25 cdot 16 = pi cdot 25 cdot 16 = 400 pi : см^3 approx 1 256.63706 : см^3

Ответ: 400 pi : см^3 approx 1 256.63706 : см^3

Проверить ответ поможет калькулятор .

Источник

4.png

Рис. (1). Цилиндр

Площадь поверхности цилиндра состоит из площади боковой поверхности и площади оснований цилиндра.

Площадь боковой поверхности цилиндра

где (R) — радиус цилиндра,

(H) — высота цилиндра

р 7.png

Рис. (2). Боковая поверхность цилиндра

Развёртка боковой поверхности цилиндра на плоскости — прямоугольник.

Одна сторона прямоугольника является  высотой цилиндра.

(AB = H).

Вторая сторона прямоугольника является длиной окружности основания цилиндра.

Основания цилиндра — круги.  (S(круга) =)

πR2

.

Площадь полной поверхности цилиндра равна:

(S(полн.) = 2S(осн.) + S(бок.) =)

2πR2

 (+)

2πRH

.

Объём цилиндра (V)(цилиндра) (=)

πR2
·H

.

Источники:

Рис. 1. Цилиндр, © ЯКласс.
Рис. 2. Боковая поверхность цилиндра, © ЯКласс. 

Источник

Добавить комментарий