Как найти объем с помощью архимедовой силы - Сайт, где вы сможете решить свои вопросы

Опубликовано 3 года назад по предмету
Физика
от mumea

Как найти объём тела через силу Архимеда

Ответ

Ответ дан
Helenn2

FA=pgV, где V-объем погруженного тела
p- плотность жидкость
g=9,8 Н/кг

Поэтому V=FA/pg

Самые новые вопросы

Математика – 3 года назад

Решите уравнения:
а) 15 4 ∕19 + x + 3 17∕19 = 21 2∕19;
б) 6,7x – 5,21 = 9,54

Информатика – 3 года назад

Помогите решить задачи на паскаль.1)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти произведение всех элементов массива.2)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти сумму четных элементов массива.3)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива.4)
дан массив случайных чисел (количество элементов
вводите с клавиатуры). найти максимальный элемент массива среди элементов,
кратных 3.

География – 3 года назад

Почему япония – лидер по выплавке стали?

Математика – 3 года назад

Чему равно: 1*(умножить)х? 0*х?

Русский язык – 3 года назад

В каком из предложений пропущена одна (только одна!) запятая?1.она снова умолкла, точно некий внутренний голос приказал ей замолчать и посмотрела в зал. 2.и он понял: вот что неожиданно пришло к нему, и теперь останется с ним, и уже никогда его не покинет. 3.и оба мы немножко удовлетворим свое любопытство.4.впрочем, он и сам только еле передвигал ноги, а тело его совсем застыло и было холодное, как камень. 5.по небу потянулись облака, и луна померкла.

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Источник

Дан 1 ответ

Исходная формула F(А)=р(ж) х V(т), где р(ж) – плотность жидкости, а V(т) – объем тела. Из этого получается формула V(т) = F(А)/р(ж)

morganadi_zn

17 Апр, 18

Источник

Нахождение погруженного в жидкость объема тела через силу Архимеда

Задача обратная задаче расчета силы Архимеда, по известной силе Архимеда найти объем тела.

Задача обратная задаче расчета силы Архимеда см. Сила Архимеда, по известной силе Архимеда найти объем тела, погруженный в воду.

Поскольку сила Архимеда нам известна и соответствует она объему вытесненной жидкости — то есть, той части объема тела, которая погрузилась в воду, — калькулятор получается в одно действие:
$V=frac{F_A}{{rho}{g}}$

Нахождение объема тела через силу Архимеда

Ускорение св. падения, м/с2

Ускорение свободного падения, м/с2

Точность вычисления

Знаков после запятой: 6

Ссылка скопирована в буфер обмена

Описание[править | править код]

Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.

Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.

Плавание тела. Сила Архимеда ( $F_{A}$ ) уравновешивает вес тела ( $F_{p}$ ):

${displaystyle F_{A}=F_{p};}$
ρ_ж g V_ж = ρ_т g V_т

Например, воздушный шарик объёмом , наполненный гелием, летит вверх из-за того, что плотность гелия ( ${displaystyle rho _{He}}$ ) меньше плотности воздуха ( ${displaystyle rho _{air}}$ ):

${displaystyle F_{A}>F_{p};}$

${displaystyle rho _{air}gV>rho _{He}gV.}$

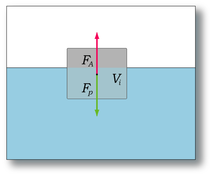
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление ( ${displaystyle P_{A}}$ ) и сила давления ( ${displaystyle F_{A}}$ ), действующие на верхнюю грань тела, равны:

${displaystyle P_{A}=rho gh_{A};}$

${displaystyle F_{A}=rho gh_{A}S,}$

где:

Давление ( ${displaystyle P_{B}}$ ) и сила давления ( ${displaystyle F_{B}}$ ), действующие на нижнюю грань тела, равны:

${displaystyle P_{B}=rho gh_{B};}$

${displaystyle F_{B}=rho gh_{B}S,}$

где:

Сила давления жидкости или газа на тело определяется разностью сил ${displaystyle F_{B}}$ и ${displaystyle F_{A}}$ :

${displaystyle F_{B}-F_{A}=rho gh_{B}S-rho gh_{A}S=rho gleft(h_{B}-h_{A}right)S=rho ghS=rho gV,}$

где:

Разница давлений:

${displaystyle P_{B}-P_{A}=rho gh_{B}-rho gh_{A}=rho gh.}$

В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляцию жилых отсеков космических аппаратов необходимо производить принудительно вентиляторами.

Обобщения[править | править код]

Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.

Вывод закона Архимеда для тела произвольной формы[править | править код]

Вывод через мысленный эксперимент[править | править код]

Если мысленно заменить погружённое в жидкость тело той же жидкостью, мысленно размещённая в том же объёме порция воды будет находиться в равновесии и действовать на окружающую воду с силой, равной силе тяжести, действующей на порцию воды. Так как перемешивания частиц воды не происходит, можно утверждать, что окружающая вода действует на выделенный объём с той же силой, но направленной в противоположном направлении, то есть с силой, равной ^[4]^[5]^[6].

Расчёт силы[править | править код]

Гидростатическое давление на глубине , оказываемое жидкостью с плотностью rho на тело, есть . Пусть плотность жидкости ( rho ) и напряжённость гравитационного поля () — постоянные величины, а — параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат Oxyz , причём выберем направление оси z совпадающим с направлением вектора . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку . На неё будет действовать сила давления жидкости, направленная внутрь тела, $d{vec {F}}_{A}=-pd{vec {S}}$ . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:

${displaystyle {vec {F}}_{A}=-int limits _{S}{p,d{vec {S}}}=-int limits _{S}{rho gh,d{vec {S}}}=-rho gint limits _{S}{h,d{vec {S}}}=^{*}-rho gint limits _{V}{operatorname {grad} (h),dV}=^{**}-rho gint limits _{V}{{vec {e}}_{z}dV}=-rho g{vec {e}}_{z}int limits _{V}{dV}=(rho gV)(-{vec {e}}_{z}).}$

При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.

${displaystyle {}^{*}h(x,y,z)=z;}$

${displaystyle ^{**}operatorname {grad} h=nabla h={vec {e}}_{z}.}$

Получаем, что модуль силы Архимеда равен , и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.

Вывод через закон сохранения энергии[править | править код]

Закон Архимеда можно также вывести из закона сохранения энергии. Работа силы, действующей со стороны погружённого тела на жидкость, приводит к изменению её потенциальной энергии:

${displaystyle A=-F*(h_{1}-h_{2})=-Delta E_{p}=-m_{text{ж}}gDelta h,}$

где ${displaystyle m_{text{ж}}}$ — масса вытесненной части жидкости, Delta h — перемещение её центра масс. Отсюда модуль вытесняющей силы:

${displaystyle F=m_{text{ж}}g.}$

По третьему закону Ньютона эта сила, равна по модулю и противоположна по направлению силе Архимеда, действующей со стороны жидкости на тело. Объём вытесненной жидкости равен объёму погруженной части тела, поэтому массу вытесненной жидкости можно записать как:

${displaystyle m_{text{ж}}=rho _{text{ж}}V_{text{т}},}$

где ${displaystyle V_{text{т}}}$

— объем погружённой части тела.

Таким образом, для силы Архимеда имеем:

${displaystyle F_{A}= F=m_{text{ж}}g=rho _{text{ж}}gV_{text{т}}.}$

Условие плавания тел[править | править код]

Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести ${displaystyle F_{T}}$ и силы Архимеда ${displaystyle F_{A}}$ , которые действуют на это тело. Возможны следующие три случая:

${displaystyle F_{T}>F_{A}}$ — тело тонет;
${displaystyle F_{T}=F_{A}}$ — тело плавает в жидкости или газе;
${displaystyle F_{T}<F_{A}}$ — тело всплывает до тех пор, пока не начнёт плавать.

Другая формулировка (где ${displaystyle rho _{t}}$ — плотность тела, ${displaystyle rho _{s}}$ — плотность среды, в которую тело погружено):

${displaystyle rho _{t}>rho _{s}}$ — тело тонет;
${displaystyle rho _{t}=rho _{s}}$ — тело плавает в жидкости или газе;
${displaystyle rho _{t}<rho _{s}}$ — тело всплывает до тех пор, пока не начнёт плавать.

Примечания[править | править код]

↑ Архимеда закон : [арх. 1 января 2023] // Анкилоз — Банка. — М. : Большая российская энциклопедия, 2005. — С. 331. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 2). — ISBN 5-85270-330-3.
↑ Архимеда закон // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 123. — 707 с. — 100 000 экз.
↑ Всё написанное ниже, если не оговорено иное, относится к однородному полю силы тяжести (например, к полю, действующему вблизи поверхности планеты).
↑ Перышкин А. , Оригинальное доказательство закона Архимеда. Дата обращения: 28 сентября 2020. Архивировано 20 июля 2020 года.
↑ Доказательство закона Архимеда для тела произвольной формы. Дата обращения: 28 сентября 2020. Архивировано 21 сентября 2020 года.
↑ Buoyancy (англ.). Архивировано 14 июля 2007 года.

Ссылки[править | править код]

Архимедов закон // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Закон Архимеда // Энциклопедия «Кругосвет».

Источник

Как найти объём тела через силу Архимеда

Информация

Нахождение объема тела через силу Архимеда

Похожие калькуляторы

Экзотические единицы длины

Чей фунт тяжелее?

Уровень жидкости в наклоненном цилиндрическом баке

Температурные шкалы

Старинные русские деньги

Соответствие размеров обуви

Системы измерения плоских углов

Рост в русской системе мер

Размер экрана

Размер снимка в пикселях и формат фотографии

Перевод числа плиток в единицы площади и обратно

Перевод мер площади из метрической в английскую систему и обратно

Перевод мер длины из русской системы в метрическую и обратно

Перевод мер длины из метрической в имперскую систему и обратно

Перевод кельвинов в градусы цельсия

Перевод из фунтов в килограммы и обратно

Перевод из фунтов в дюймы

Перевод из градусов Фаренгейта в градусы Цельсия

Перевод дробных чисел из одной системы счисления в другую

Перевод градусов Цельсия в градусы Фаренгейта

Перевод градусов минут и секунд в десятичные градусы и обратно

Перевод градусов в радианы

Объем сегмента цилиндра

Объем жидкости в наклоненном цилиндрическом баке

Общее время наработки аппарата

Сочетание цветов

О римских цифрах

Метров в секунду и километров в час

Конвертер единиц давления

Калькулятор горловины для цилиндрического бака

Описание[править | править код]

Обобщения[править | править код]

Вывод закона Архимеда для тела произвольной формы[править | править код]

Вывод через мысленный эксперимент[править | править код]

Расчёт силы[править | править код]

Вывод через закон сохранения энергии[править | править код]

Условие плавания тел[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Как найти маленькие магниты

Как можно найти сжатие

Как найти золотое украшение в песке

Добавить комментарий Отменить ответ