Шар — это тело, все точки которого находятся от заданой точки на расстоянии, не превышающем R.
Онлайн-калькулятор объема шара
Заданная точка, о которой говорится в определении шара называется центром этого шара. А упомянутое расстояние — радиусом данного шара.
У шара, по аналогии с кругом, так же есть диаметр DD, который по длине в два раза больше радиуса:
D=2⋅RD=2cdot R
Формула объема шара через его радиус
Объем шара вычисляется по следующей формуле:
V=43⋅π⋅R3V=frac{4}{3}cdotpicdot R^3
RR — радиус данного шара.
Рассмотрим несколько примеров.
Шар вписан в куб, диагональ dd которого равна 500 см.sqrt{500}text{ см.} Найти объем шара.
Решение
d=500d=sqrt{500}
Для начала необходимо определить длину стороны куба. Будем считать, что она равна aa. Следовательно, диагональ куба, равна (исходя из теоремы Пифагора):
d=a2+a2+a2d=sqrt{a^2+a^2+a^2}
d=3⋅a2d=sqrt{3cdot a^2}
d=3⋅ad=sqrt{3}cdot a
500=3⋅asqrt{500}=sqrt{3}cdot a
a=5003a=sqrt{frac{500}{3}}
a≈12.9aapprox12.9
Если в куб вписан шар, то его радиус равен половинке длины стороны этого куба. В результате имеем:
R=12⋅aR=frac{1}{2}cdot a
R=12⋅12.9≈6.4R=frac{1}{2}cdot 12.9approx6.4
Заключительный этап — нахождение объема шара по формуле:
V=43⋅π⋅R3≈43⋅π⋅(6.4)3≈1097,5 см3V=frac{4}{3}cdotpicdot R^3approxfrac{4}{3}cdotpicdot (6.4)^3approx1097,5text{ см}^3
Ответ
1097,5 см3.1097,5text{ см}^3.
Формула объема шара через его диаметр
Так же объем шара можно найти через его диаметр. Для этого используем связь между радиусом и диаметром шара:
D=2⋅RD=2cdot R
R=D2R=frac{D}{2}
Подставим это выражение в формулу для объема шара:
V=43⋅π⋅R3=43⋅π⋅(D2)3=π6⋅D3V=frac{4}{3}cdotpicdot R^3=frac{4}{3}cdotpicdotBig(frac{D}{2}Big)^3=frac{pi}{6}cdot D^3
V=π6⋅D3V=frac{pi}{6}cdot D^3
DD — диаметр данного шара.
Диаметр шара равен 15 см.15text{ см.} Найдите его объем.
Решение
D=15D=15
Сразу подставляем значение диаметра в формулу:
V=π6⋅D3=π6⋅153≈1766.25 см3V=frac{pi}{6}cdot D^3=frac{pi}{6}cdot 15^3approx1766.25text{ см}^3
Ответ
1766.25 см3.1766.25text{ см}^3.
Не знаете, где оформить выполнение контрольных работ на заказ? Профильные эксперты Студворк помогут вам с решением!
Тест по теме «Объем шара»

{V= dfrac{4}{3} pi R^3}
На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.
Шар – это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.
Содержание:
- калькулятор объема шара
- формула объема шара через радиус
- формула объема шара через диаметр
- формула объема шара через длину окружности
- формула объема шара через площадь поверхности
- примеры задач
Формула объема шара через радиус

{V = dfrac{4}{3} pi R^3}
R – радиус шара
Формула объема шара через диаметр
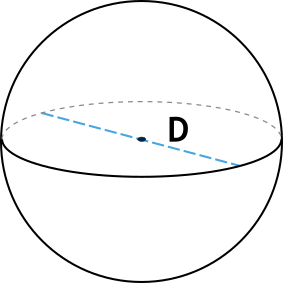
{V = dfrac{1}{6} pi D^3}
D – диаметр шара
Формула объема шара через длину окружности
Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2pi r}
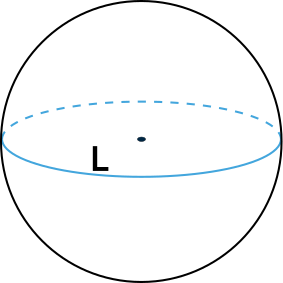
{V = dfrac{L^3}{6 pi^2}}
L – длина окружности
Формула объема шара через площадь поверхности
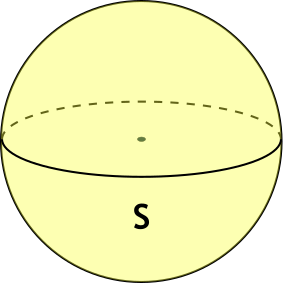
{V = sqrt{ dfrac{S^3}{36 pi}}}
S – площадь поверхности
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объем шара радиус которого равен 12см.
Решение
Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.
V = dfrac{4}{3} pi R^3 = dfrac{4}{3} pi cdot 12^3 = dfrac{4}{3} pi cdot 1728 = dfrac{4 cdot 1728}{3} pi = 2304 cdot pi : см^3 approx 7238.22947 : см^3
Ответ: 2304 cdot pi : см^3 approx 7238.22947 : см^3
Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .
Задача 2
Найдите объем шара диаметр которого равен 12см.
Решение
В этой задаче воспользуемся формулой шара через диаметр.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 12^3 = dfrac{1}{6} pi cdot 1728 = dfrac{1728}{6} pi = 288 pi : см^3 approx 904.77868 : см^3
Ответ: 288 pi : см^3 approx 904.77868 : см^3
И снова в проверке ответа нам поможет калькулятор .
Задача 3
Найдите объем шара диаметр которого равен 6см.
Решение
Эта задача аналогична задаче 2.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 6^3 = dfrac{1}{6} pi cdot 216 = dfrac{216}{6} pi = 36 pi : см^3 approx 113.09734 : см^3
Ответ: 36 pi : см^3 approx 113.09734 : см^3
И снова в проверке ответа нам поможет калькулятор .
В данной публикации мы рассмотрим, как можно найти объем шара и разберем примеры решения задач для закрепления материала.
-
Формула вычисления объема шара
- Примеры задач
Формула вычисления объема шара
1. Через радиус
Объем (V) шара равняется четырем третьим произведения его радиуса в кубе и числа π.


Примечание: в расчетах значение числа π округляется до 3,14.
2. Через диаметр
Диаметр шара равняется двум его радиусам: d = 2R. А значит, формула вычисления объема может выглядеть следующим образом:

Примеры задач
Задание 1
Вычислите объем шара, если его радиус равняется 3 см.
Решение:
Применив первую формулу (через радиус) получаем:![]()
Задание 2
Найдите объем шара, если известно, что его диаметр равен 12 см.
Решение:
Используем вторую формулу, в которой задействован диаметр:![]()
|
Нужно знать его радиус. Умножить 4/3 на число “пи” и на радиус шара в третьей степени. К примеру, объем шара с радиусом 2 метра будет: 4/3х3,14х8=33,5 куб.метра автор вопроса выбрал этот ответ лучшим
Алиса в Стране 5 лет назад Все, что нам нужно для вычисления объема шара – это просто знать его радиус и нехитрую формулу для расчета. Формула вот такая:
Допустим, радиус нашего шара равен 10 сантиметрам, подставляем 10 см в нашу формулу и получаем: V = 4/3 х 3,14 х 1000 = 4187 кубических сантиметров.
Марина Вологда 5 лет назад Чтобы найти объем шара (сферы) следует знать его радиус или диаметр. Если радиус шара (сферы) известен, применяем следующую формулу:
Где “r” – радиус шара. Известно, что “Пи” всегда равно 3,14. Так же иногда в задачах дается диаметр шара (сферы). Если известен диаметр шара, применяется следующая формула:
Где “d” – это диаметр.
Любопытство 5 лет назад В выпускном, одиннадцатом (насколько я помню) классе учат находить объём шара вот так: высчитывают его по формуле: 4/3 Пи Х радиус в кубе. Думаю, что значение Пи всем известно, но на всякий случай сообщаю: π = 3,14.
В Рокотов 5 лет назад Сначала определимся что такое шар – это точки пространства равноудаленные от центра шара. Чтобы найти объем шара, при известном значении пи (3,14), нужно знать значения его радиуса или половины радиуса -диаметра, при известном радиусе искомое можно получить по формуле:
Zolotynka 5 лет назад Для начала разберемся, что представляет собой такая геометрическая фигура как шар. Итак, шар – это твердое тело, у которого есть особенность: любая точка на поверхности шара будет находиться на одном и том же расстоянии от его центра. Данное расстояние известно как радиус. Максимально прямое расстояние через центр шара принято называть диаметром. Диаметр -вдвое больше радиуса. Теперь посмотрим, как найти объем шара? Объем сферы равен четырем третям произведения числа pi и радиуса, возведенного в куб. Формула будет выглядеть следующим образом:
** Число pi, в задачах принято сокращать до двух десятых- 3,14.
Ninaarc 5 лет назад Шар представляет собой часть пространства, которое ограничено сферой. Для определения объема шара имеется специальная формула, в которую следует подставить нужные значения. Формула для вычисления объема шара выглядит таким образом:
Из формулы становится ясно, что нам должен быть известен радиус шара (r), который затем потребуется возвести в третью степень. А число ПИ нам хорошо известно, оно в числовом значении выглядит так: π = 3,14.
Трибунька 8 лет назад Чтобы вычислить объем шара надо знать формулу, где R – радиус шара.
Вот есть отличный сайт где можно онлайн высчитать объём шара. Этот сайт очень полезен для школьников, так как там много формул по геометрии, математике, физике и химии. Кроме формул некоторые задачи можно решить сразу на сайте. Есть справочные таблицы. Сайт очень удобно и грамотно сделан, все легко и просто на нём искать.
Нахождение объема шара, тема урока по Геометрии, если я не ошибаюсь, одиннадцатого класса общеобразовательной школы. Для нахождения объема геометрического тела Шар, нужно знать диаметр диаметр этого тела, разделив который на два получим его радиус. А далее подставляем это значение (радиус) в ниже приведенную формулу, и на выходе получаем объем шара.
РУДЬКО 5 лет назад Объём шара, это всем известная формула, которая на словах звучит как “четыре третьих пи эр в кубе”. То есть это проиизведение частного от 43 умноженное на число “Пи” и радиуса шара, возведённого в третью степень, то есть в “куб”.
vksvovko 6 лет назад 4/3*Пи*радиус в кубе. это и есть объем шара. Есть ещё один интересный способ – опустить его в измерительную емкость с водой, и сколько он вытеснит воды столько и его объем. таким способом можно измерять любой предмет. Знаете ответ? |
Калькулятор объема шара
Рассчитайте онлайн объем любой шарообразной фигуры по ее радиусу или диаметру.
Что известно
Длина
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое калькулятор объема шара или сферы?
Калькулятор объема шара — это онлайн инструмент, который используется для быстрого расчета объема шара по его радиусу или диаметру. Объем шара представляет собой объем пространства, которое занимает шар в трехмерном пространстве.
Калькулятор объема шара может быть полезным инструментом для учебных заданий или практических задач, связанных с расчетами объемов шаров. Он также может использоваться в различных профессиональных областях, где необходимы точные расчеты объемов, например, в архитектуре, инженерии, физике и т.д.
🌎 Где можно применить калькулятор объема шара?

Калькулятор объема шара может быть полезным инструментом в различных областях и сферах деятельности, например:
- Архитектура и строительство: при проектировании и строительстве куполов, бассейнов, шарообразных крыш и других шарообразных конструкций.
- Медицина: при расчете объема опухолей, кровеносных сосудов, сердца и других органов.
- Производство и промышленность: при расчете объема шарообразных резервуаров, емкостей, шарообразных деталей и т.д.
- Космология: при расчете объема планет, галактик и других космических объектов.
- Физика: при расчете объема и массы материалов, например, при изучении свойств и характеристик материалов.
- Образование: при выполнении учебных заданий и проектов в школе, вузе и других образовательных учреждениях.
- Различные хобби и увлечения: при создании шарообразных фигур, скульптур, шариков для игр и других творческих проектов.
Калькулятор объема шара может быть полезным инструментом во многих ситуациях, когда необходимо быстро и точно вычислить объем шара.
🔮 В чем преимущество шарообразной формы?
Шарообразная форма имеет несколько преимуществ, которые делают ее полезной в различных областях:
- Минимальная поверхность: шарообразная форма имеет минимальную поверхность в отношении своего объема. Это значит, что на единицу объема шара приходится меньше поверхности, чем на единицу объема других форм, что может быть полезно, например, для сокращения издержек при производстве.
- Равномерность нагрузки: шарообразная форма имеет равномерное распределение нагрузки на поверхности, что позволяет ей лучше выдерживать внешнее давление.
- Сферическая симметрия: шарообразная форма имеет сферическую симметрию, что означает, что она выглядит одинаково при любом повороте вокруг своей оси. Это может быть полезным, например, при проектировании оптических систем, таких как линзы и зеркала.
- Простота: шарообразная форма является одной из самых простых геометрических форм, и ее параметры (радиус, диаметр, объем и т.д.) легко вычисляются.
- Эстетика: шарообразная форма считается эстетичной и привлекательной для взгляда. Она широко используется в дизайне, искусстве и архитектуре для создания красивых и уникальных форм.
Как вычислить объем шара через радиус?
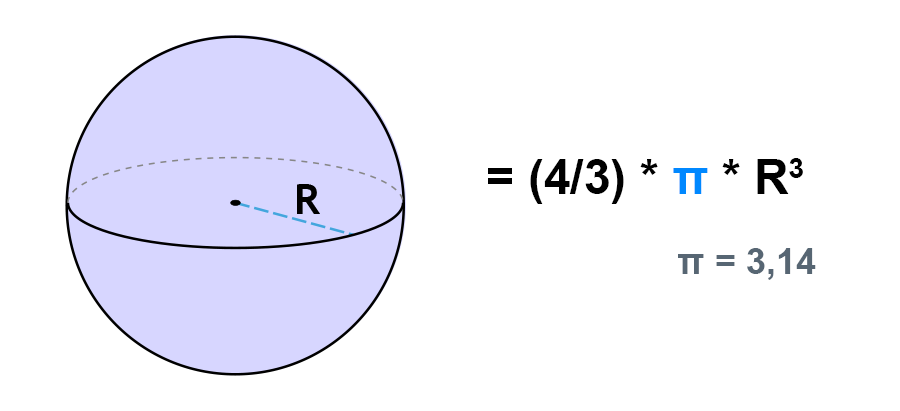
Калькулятор объема шара обычно использует стандартную математическую формулу для расчета объема шара, которая основана на его радиусе. Формула для расчета объема шара выглядит следующим образом:
V = (4/3) * π * r3
где V – объем шара, r – радиус шара, pi – константа, примерно равная 3.14159.
Как вычислить объем шара через диаметр?
Чтобы вычислить объем шара через его диаметр, можно использовать следующую формулу:
V = (4/3) * π * (d/2)3
где V – объем шара, d – диаметр шара, π – число Пи, математическая константа, равная приблизительно 3,14159.
Для расчета объема шара нужно возвести значение d/2 в куб и умножить результат на 4/3 и на π.
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемы вопросе о шаре и его объеме.
Как пользоваться онлайн калькулятором объема шара?
Для того, чтобы использовать калькулятор объема шара, нужно ввести значение радиуса шара или его диаметра в соответствующее поле калькулятора, затем калькулятор автоматически рассчитает объем шара.
Что такое шар?
Шар — это трехмерная геометрическая фигура, которая представляет собой идеальную сферу в трёхмерном пространстве. Все точки поверхности шара находятся на одинаковом расстоянии от его центра.
Для чего нужен расчет объема шара?
Расчет объема шара может быть полезен для решения различных задач в науке, технике и повседневной жизни. Например, зная объем шара, можно вычислить массу сферического объекта, если известна его плотность. Также расчет объема шара может использоваться при проектировании сферических емкостей или устройств.
Какой материал лучше всего подходит для изготовления шаров?
Для изготовления шаров часто используют различные материалы, в том числе металлы, стекло, пластмассу и резину. Выбор материала зависит от конкретной задачи и требований к изделию. Например, если необходима высокая прочность, то лучше выбрать металлический шар, а если необходимо обеспечить прозрачность, то следует выбрать стеклянный шар.
Как найти радиус шара, если известен его объем?
Радиус шара может быть найден по формуле: r = ³√(3V/4π), где r – радиус шара, V – объем шара, π – число пи (3.14159265…).
Как найти диаметр шара, если известен его радиус?
Диаметр шара равен удвоенному радиусу, то есть d = 2r, где d – диаметр шара, r – радиус шара.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии










