Вычисление объёмов
Объём тела, ограниченного сверху и снизу поверхностями $mathbf { textit { z } } =mathbf { textit { f } } _ { 1 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $mathbf { textit { z } } =mathbf { textit { f } } _ { 2 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $(x,y)in D$, с боков – цилиндрической поверхностью с образующими, параллельными оси $mathbf { textit { Oz } } $, равен $v=iintlimits_D { left[ { f_1 (x,y)-f_2 (x,y) }right]dxdy } $; эта формула очевидно следует из геометрического смысла двойного интеграла.
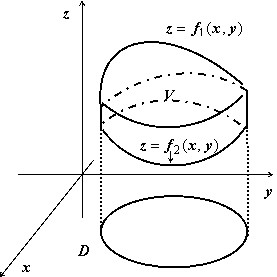
Основной вопрос, который надо решить – на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.
Пример 1
Найти объём тела $V:left[{ begin{array} { l } y=0,;z=0, \ x+y+z=4,; \ 2x+z=4. \ end{array} }right.$
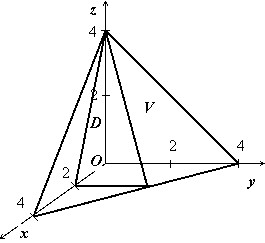
Решение:
Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $mathbf { textit { Oxz } } $:
$V:left[{ begin{array} { l } (x,z)in D, \ 0leqslant yleqslant 4-x-z. \ end{array} }right.$
Область $mathbf { textit { D } } $ – треугольник, ограниченный прямыми $mathbf { textit { x } } $ = 0, $mathbf { textit { z } } $ = 0, 2$mathbf { textit { x } } +mathbf { textit { z } } $ = 4, поэтому
$V=iintlimits_D { (4-x-z)dxdz } =intlimits_0^2 { dxintlimits_0^ { 4-2x } { (4-x-z)dz } } = intlimits_0^2 { dxleft. { left( { 4z-xz-z^2/2 }right) }right|_0^ { 4-2x } } = intlimits_0^2 { left[ { 16-8x-4x+2x^2-(4-2x)^2/2 }right]dx } = \ = intlimits_0^2 { left( { 8-4x }right)dx } = left. { left( { 8x-2x^2 }right) }right|_0^2 =16-8=8$
Пример 2
Найти объём области, ограниченной поверхностями $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { R } } ^ { 2 } $,
$(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$.
Решение:
Первая поверхность – сфера, вторая – цилиндрическая – с образующими, параллельными оси $mathbf { textit { Oz } } $ { в уравнении нет $mathbf { textit { z } } $ в явной форме). Построить в плоскости $mathbf { textit { Oxy } } $ кривую шестого порядка, заданную уравнением $(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей { чётные степени } и точка $mathbf { textit { О } } (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(cos ^4varphi +sin ^4varphi );r^2=R^2((cos ^2varphi +sin ^2varphi )^2-2cos ^2varphi sin ^2varphi )=R^2(1-frac { sin ^22varphi } { 2 } )=$
$=R^2(1-frac { 1-cos 4varphi } { 4 } )=R^2frac { 3+cos 4varphi } { 4 } ;r=Rfrac { sqrt { 3+cos 4varphi } } { 2 } .$ Эту кривую построить уже можно. $r(varphi )$ максимально, когда $cos 4varphi =1;(varphi =0,frac { 2pi } { 4 } =frac { pi } { 2 } ,frac { 4pi } { 4 } =pi ,frac { 6pi } { 4 } =frac { 3pi } { 2 } )$, минимально, когда
$cos 4varphi =-1;(varphi =frac { pi } { 4 } ,frac { 3pi } { 4 } ,frac { 5pi } { 4 } ,frac { 7pi } { 4 } ),$ и гладко меняется между этими пределами { точка $mathbf { textit { О } } (0,0)$ не принадлежит этой кривой, где мы её потеряли? } .
Пользуясь симметрией, получаем $ V=16iintlimits_D { sqrt { R^2-x^2-y^2 } dxdy= } 16iintlimits_D { sqrt { R^2-r^2 } rdrdvarphi = } =16intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } rdr } = $ $ =-8intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } d(R^2-r^2) } =-8frac { 2 } { 3 } intlimits_0^ { frac { pi } { 4 } } { left. { (R^2-r^2)^ { frac { 3 } { 2 } } }right|_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } dvarphi } =-frac { 16 } { 3 } R^3intlimits_0^ { frac { pi } { 4 } } { left. { left[ { left( { frac { sin ^22varphi } { 2 } }right)^ { frac { 3 } { 2 } } -1 }right] }right|dvarphi } = $ и т.д.
Пример 3
Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)
Решение:
Данное тело показано на рисунке.
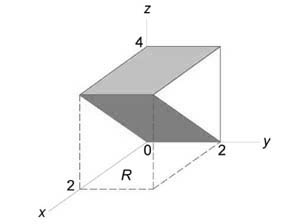
Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 – x.) Тогда объем равен $ { V = iintlimits_R { left[ { left( { 4 – x }right) – x }right]dxdy } } = { intlimits_0^2 { left[ { intlimits_0^2 { left( { 4 – 2x }right)dy } }right]dx } } = { intlimits_0^2 { left[ { left. { left( { 4y – 2xy }right) }right|_ { y = 0 } ^2 }right]dx } } = { intlimits_0^2 { left( { 8 – 4x }right)dx } } = { left. { left( { 8x – 2 { x^2 } }right) }right|_0^2 } = { 16 – 8 = 8. } $
Пример 4
Описать тело, объем которого определяется интегралом (V = intlimits_0^1 { dx } intlimits_0^ { 1 – x } { left( { { x^2 } + { y^2 } }right)dy } .)
Решение:
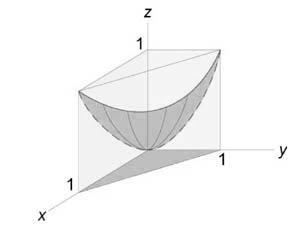
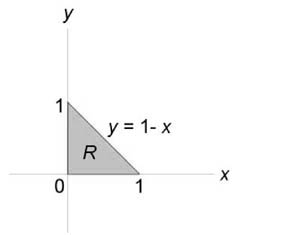
Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 – x) ниже параболической поверхности (z = { x^2 } + { y^2 } .) Объем тела равен $ { V = intlimits_0^1 { dx } intlimits_0^ { 1 – x } { left( { { x^2 } + { y^2 } }right)dy } } = { intlimits_0^1 { left[ { left. { left( { { x^2 } y + frac { { { y^3 } } } { 3 } }right) }right|_ { y = 0 } ^ { 1 – x } }right]dx } } = { intlimits_0^1 { left[ { { x^2 } left( { 1 – x }right) + frac { { { { left( { 1 – x }right) } ^3 } } } { 3 } }right]dx } } = \ = { intlimits_0^1 { left( { { x^2 } – { x^3 } + frac { { 1 – 3x + 3 { x^2 } – { x^3 } } } { 3 } }right)dx } } = { intlimits_0^1 { left( { 2 { x^2 } – frac { { 4 { x^3 } } } { 3 } – x + frac { 1 } { 3 } }right)dx } } = { left. { left( { frac { { 2 { x^3 } } } { 3 } – frac { 4 } { 3 } cdot frac { { { x^4 } } } { 4 } – frac { { { x^2 } } } { 2 } + frac { x } { 3 } }right) }right|_0^1 } = { frac { 2 } { 3 } – frac { 1 } { 3 } – frac { 1 } { 2 } + frac { 1 } { 3 } = frac { 1 } { 6 } . } $
Пример 5
Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)
Решение:
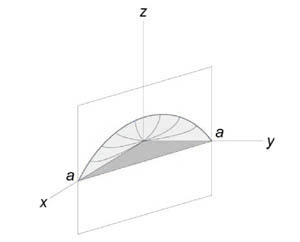
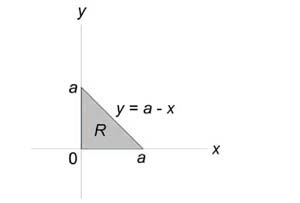
Данное тело лежит над треугольником (R) в плоскости (Oxy) ниже поверхности (z = xy.) Объем тела равен $ { V = iintlimits_R { xydxdy } } = { intlimits_0^a { left[ { intlimits_0^ { a – x } { xydy } }right]dx } } = { intlimits_0^a { left[ { left. { left( { frac { { x { y^2 } } } { 2 } }right) }right|_ { y = 0 } ^ { a – x } }right]dx } } = { frac { 1 } { 2 } intlimits_0^a { x { { left( { a – x }right) } ^2 } dx } } = { frac { 1 } { 2 } intlimits_0^a { xleft( { { a^2 } – 2ax + { x^2 } }right)dx } } = \ = { frac { 1 } { 2 } intlimits_0^a { left( { { a^2 } x – 2a { x^2 } + { x^3 } }right)dx } } = { frac { 1 } { 2 } left. { left( { { a^2 } cdot frac { { { x^2 } } } { 2 } – 2a cdot frac { { { x^3 } } } { 3 } + frac { { { x^4 } } } { 4 } }right) }right|_0^a } = { frac { 1 } { 2 } left( { frac { { { a^2 } } } { 2 } – frac { { 2 { a^4 } } } { 3 } + frac { { { a^4 } } } { 4 } }right) } = { frac { { { a^4 } } } { { 24 } } . } $
Пример 6
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( { x^2 } + { y^2 } = 1,) (z = 1 – x.)
Решение:
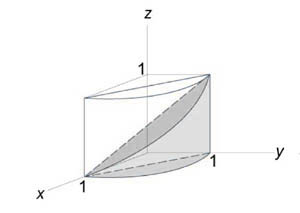
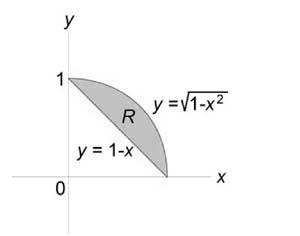
Как видно из рисунков, в области интегрирования (R) при (0 le x le 1) значения (y) изменяются от (1 – x) до (sqrt { 1 – { x^2 } } .)
Сверху тело ограничено плоскостью (z = 1 – x.) Следовательно, объем данного тела равен $ { V = iintlimits_R { left( { 1 – x }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_ { 1 – x } ^ { sqrt { 1 – { x^2 } } } { left( { 1 – x }right)dy } }right]dx } } = { intlimits_0^1 { left[ { left( { 1 – x }right)left. y right|_ { 1 – x } ^ { sqrt { 1 – { x^2 } } } }right]dx } } = { intlimits_0^1 { left( { 1 – x }right)left( { sqrt { 1 – { x^2 } } – 1 + x }right)dx } } = \ = { intlimits_0^1 { left( { sqrt { 1 – { x^2 } } – xsqrt { 1 – { x^2 } } – 1 + 2x – { x^2 } }right)dx } } = { intlimits_0^1 { sqrt { 1 – { x^2 } } dx } } – { intlimits_0^1 { xsqrt { 1 – { x^2 } } dx } } – { intlimits_0^1 { left( { 1 + 2x – { x^2 } }right)dx } . } $
Вычислим полученные три интеграла отдельно. $ { I_1 } = intlimits_0^1 { sqrt { 1 – { x^2 } } dx } .$ Сделаем замену: (x = sin t.) Тогда (dx = cos tdt.) Видно, что (t = 0) при (x = 0) и (t = largefrac { pi } { 2 } normalsize) при (x = 1.) Следовательно, $ { { I_1 } = intlimits_0^1 { sqrt { 1 – { x^2 } } dx } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { sqrt { 1 – { { sin } ^2 } t } cos tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { { { cos } ^2 } tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { frac { { 1 + cos 2t } } { 2 } dt } } = { frac { 1 } { 2 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { left( { 1 + cos 2t }right)dt } } = { frac { 1 } { 2 } left. { left( { t + frac { { sin 2t } } { 2 } }right) }right|_0^ { largefrac { pi } { 2 } normalsize } } = { frac { 1 } { 2 } left( { frac { pi } { 2 } + frac { { sin pi } } { 2 } }right) = frac { pi } { 4 } . } $ { Сравните с площадью сектора единичного круга в первом квадранте).
Вычислим второй интеграл ( { I_2 } = intlimits_0^1 { xsqrt { 1 – { x^2 } } dx } ,) используя замену переменной. Полагаем (1 – { x^2 } = w.) Тогда (-2xdx = dw) или (xdx = largefrac { { – dw } } { 2 } normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ { { I_2 } = intlimits_0^1 { xsqrt { 1 – { x^2 } } dx } } = { intlimits_1^0 { sqrt w left( { – frac { { dw } } { 2 } }right) } } = { – frac { 1 } { 2 } intlimits_1^0 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { { w^ { largefrac { 1 } { 2 } normalsize } } dw } } = { frac { 1 } { 2 } left. { left( { frac { { 2 { w^ { largefrac { 3 } { 2 } normalsize } } } } { 3 } }right) }right|_0^1 = frac { 1 } { 3 } . } $ Наконец, вычислим третий интеграл. $require { cancel } { { I_3 } = intlimits_0^1 { left( { 1 – 2x + { x^2 } }right)dx } } = { left. { left( { x – { x^2 } + frac { { { x^3 } } } { 3 } }right) }right|_0^1 } = { cancel { 1 } – cancel { 1 } + frac { 1 } { 3 } = frac { 1 } { 3 } . } $ Таким образом, объем тела равен $ { V = { I_1 } – { I_2 } – { I_3 } } = { frac { pi } { 4 } – frac { 1 } { 3 } – frac { 1 } { 3 } = frac { pi } { 4 } – frac { 2 } { 3 } approx 0,12. } $
Пример 7
Вычислить объем единичного шара.
Решение:
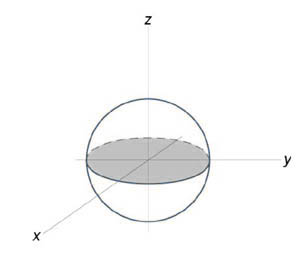
Уравнение сферы радиусом (1) имеет вид ( { x^2 } + { y^2 } + { z^2 } = 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = sqrt { 1 – left( { { x^2 } + { y^2 } }right) } .$ Преобразуя это уравнение в полярные координаты, получаем $zleft( { r,theta }right) = sqrt { 1 – { r^2 } } .$ В полярных координатах область интегрирования (R) описывается множеством (R = left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].) Следовательно, объем верхнего полушара выражается формулой $ { { V_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 – { r^2 } } rdrdtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { sqrt { 1 – { r^2 } } rdr } } = { 2pi intlimits_0^1 { sqrt { 1 – { r^2 } } rdr } . } $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 – { r^2 } = t.) Тогда (-2rdr = dt) или (rdr = – largefrac { { dt } } { 2 } normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ { { V_ { largefrac { 1 } { 2 } normalsize } } = 2pi intlimits_0^1 { sqrt { 1 – { r^2 } } rdr } } = { 2pi intlimits_1^0 { sqrt t left( { – frac { { dt } } { 2 } }right) } } = { – pi intlimits_1^0 { sqrt t dt } } = { pi intlimits_0^1 { { t^ { largefrac { 1 } { 2 } normalsize } } dt } } = { pi left. { left( { frac { { { t^ { largefrac { 3 } { 2 } normalsize } } } } { { frac { 3 } { 2 } } } }right) }right|_0^1 } = { frac { { 2pi } } { 3 } . } $ Таким образом, объем единичного шара равен $V = 2 { V_ { largefrac { 1 } { 2 } normalsize } } = frac { { 4pi } } { 3 } .$
Пример 8
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).
Решение:
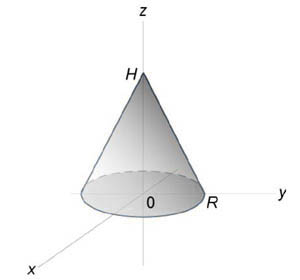
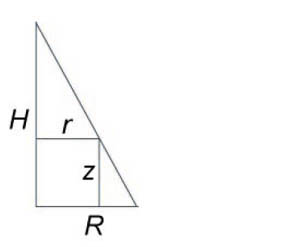
Сначала получим уравнение поверхности конуса. Используя подобные треугольники, можно записать $ { frac { r } { R } = frac { { H – z } } { H } , } ;; { text { где } ;;r = sqrt { { x^2 } + { y^2 } } . } $ Следовательно, $ { H – z = frac { { Hr } } { R } } ;; { text { или } ;;zleft( { x,y }right) } = { H – frac { { Hr } } { R } } = { frac { H } { R } left( { R – r }right) } = { frac { H } { R } left( { R – sqrt { { x^2 } + { y^2 } } }right). } $ Тогда объем конуса равен $ { V = iintlimits_R { zleft( { x,y }right)dxdy } } = { iintlimits_R { frac { H } { R } left( { R – sqrt { { x^2 } + { y^2 } } }right)dxdy } } = { frac { H } { R } iintlimits_R { left( { R – r }right)rdrdtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { left[ { intlimits_0^R { left( { R – r }right)drd } }right]dtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { dtheta } intlimits_0^R { left( { Rr – { r^2 } }right)dr } } = { frac { { 2pi H } } { R } intlimits_0^R { left( { Rr – { r^2 } }right)dr } } = \ = { frac { { 2pi H } } { R } left. { left( { frac { { R { r^2 } } } { 2 } – frac { { { r^3 } } } { 3 } }right) }right|_ { r = 0 } ^R } = { frac { { 2pi H } } { R } left( { frac { { { R^3 } } } { 2 } – frac { { { R^3 } } } { 3 } }right) } = { frac { { 2pi H } } { R } cdot frac { { { R^3 } } } { 6 } = frac { { pi { R^2 } H } } { 3 } . } $
а) Объём.
Как мы знаем, объем
V
тела, ограниченного поверхностью
![]() ,
,
где
![]() –
–
неотрицательная функция, плоскостью![]() и цилиндрической поверхностью,
и цилиндрической поверхностью,
направляющей для которой служит
граница областиD,
а образующие параллельны оси Oz,
равен двойному интегралу от функции
![]() по областиD
по областиD
:
![]()
Пример 1. Вычислить
объем тела, ограниченного поверхностями
x=0,
у=0, х+у+z=1,
z=0
(рис. 17).


Рис.17
Рис.18
Решение.
![]() D
D
– заштрихованная на рис. 17 треугольная
область в плоскости Оху,
ограниченная прямыми x=0,
у=0, x+y=1.
Расставляя пределы в двойном интеграле,
вычислим объем:
![]()
Итак,
![]() куб. единиц.
куб. единиц.
Замечание 1.
Если тело, объем которого ищется,
ограничено сверху поверхностью
![]() а снизу—поверхностью
а снизу—поверхностью![]() ,
,
причем проекцией обеих поверхностей
на плоскостьОху
является область D,
то объем V
этого тела равен разности объемов двух
«цилиндрических» тел; первое из этих
цилиндрических тел имеет нижним
основанием область D,
а верхним – поверхность
![]() второе тело имеет нижним основанием
второе тело имеет нижним основанием
также областьD,
а верхним – поверхность
![]() (рис.18).
(рис.18).
Поэтому объём V
равен разности двух двойных интегралов
:
![]()
или
![]() (1)
(1)
Легко, далее,
доказать, что формула (1) верна не только
в том случае, когда
![]() и
и![]() неотрицательны, но и тогда, когда
неотрицательны, но и тогда, когда![]() и
и![]() –
–
любые непрерывные функции, удовлетворяющие
соотношению
![]()
Замечание 2.
Если в области D
функция
![]() меняет
меняет
знак, то разбиваем область на две части:
1) областьD1
где
![]() 2) областьD2
2) областьD2
,где
![]() .
.
Предположим, что областиD1
и D2
таковы, что двойные интегралы по этим
областям существуют. Тогда интеграл
по области D1
будет положителен и будет равен
объему тела, лежащего выше плоскости
Оху. Интеграл
по D2
будет отрицателен и по абсолютной
величине равен объему тела, лежащего
ниже плоскости Оху,
Следовательно, интеграл по D
будет выражать разность соответствующих
объемов.
б) Вычисление
площади плоской области.
Если мы составим
интегральную сумму для функции
![]() по областиD,
по областиD,
то эта сумма будет равна площади S,
![]()
при любом способе
разбиения. Переходя к пределу в правой
части равенства, получим
![]()
Если область D
правильная , то площадь выразится
двукратным интегралом

Производя
интегрирование в скобках, имеем,
очевидно,
![]()
Пример 2. Вычислить
площадь области, ограниченной кривыми
![]()

Рис.19
Решение. Определим
точки пересечения данных кривых
(Рис.19). В точке пересечения ординаты
равны, т.е.
![]() ,
,
отсюда![]() Мы
Мы
получили две точки пересечения
![]()
Следовательно,
искомая площадь

5. Вычисление площади поверхности.
Пусть требуется
вычислить площадь поверхности,
ограниченной линией Г (рис.20); поверхность
задана уравнением
![]() где функция
где функция![]() непрерывна и имеет непрерывные частные
непрерывна и имеет непрерывные частные
производные. Обозначим проекцию линии
Г на плоскостьOxy
через L.
Область на плоскости Oxy,
ограниченную линией L,
обозначим D.
Разобьём произвольным
образом область D
на n
элементарных площадок
![]() В
В
каждой площадке![]() возьмём точку
возьмём точку![]() ТочкеPi
ТочкеPi
будет соответствовать на поверхности
точка
![]() Через точкуMi
Через точкуMi
проведём касательную плоскость к
поверхности. Уравнение её примет вид
![]() (1)
(1)
На этой плоскости
выделим такую площадку
![]() ,
,
которая проектируется на плоскостьОху
в виде площадки
![]() .
.
Рассмотрим сумму всех площадок![]()
Предел
![]() этой суммы, когда наибольший из диаметров
этой суммы, когда наибольший из диаметров
площадок![]() –
–
стремится к нулю, мы будем называтьплощадью
поверхности,
т. е. по определению положим
 (2)
(2)
Займемся теперь
вычислением площади поверхности.
Обозначим через
![]()
угол между
касательной плоскостью и плоскостью
Оху.

Рис.20
Рис.21
На основании
известной формулы аналитической
геометрии можно написать (рис.21)
![]()
или
![]() (3)
(3)
Угол
![]() есть в то же время угол между осьюOz
есть в то же время угол между осьюOz
и перпендикуляром к плоскости (1). Поэтому
на основании уравнения (1) и формулы
аналитической геометрии имеем
![]() Следовательно,
Следовательно,
![]()
Подставляя это
выражение в формулу (2), получим

Так как предел
интегральной суммы, стоящей в правой
части последнего равенства, по определению
представляет собой двойной интеграл
![]() то окончательно получаем
то окончательно получаем
![]() (4)
(4)
Это и есть формула,
по которой вычисляется площадь поверхности
![]()
Если уравнение
поверхности дано в виде
![]() или в виде
или в виде![]() то соответствующие формулы для вычисления
то соответствующие формулы для вычисления
поверхности имеют вид
 (3’)
(3’)
 (3’’)
(3’’)
где D’
и D’’
– области на плоскостях Oyz
и Oxz,
в которые проектируется данная
поверхность.
а) Примеры.
Пример 1. Вычислить
поверхность
![]() сферы
сферы
![]()
Решение. Вычислим
поверхность верхней половины сферы
![]() (рис.22). В этом случае
(рис.22). В этом случае
![]()
Следовательно,
подынтегральная функция примет вид
![]()
Область интегрирования
определяется условием
![]() .
.
Таким образом, на основании формулы (4)
будем иметь

Для вычисления
полученного двойного интеграла перейдём
к полярным координатам. В полярных
координатах граница области интегрирования
определяется уравнением
![]() Следовательно,
Следовательно,

Пример2. Найти
площадь той части поверхности цилиндра
![]() которая вырезается цилиндром
которая вырезается цилиндром![]()


Рис.22
Рис.23
Решение. На рис.23
изображена
![]() часть искомой поверхности. Уравнение
часть искомой поверхности. Уравнение
поверхности имеет вид![]() ;
;
поэтому
![]()
![]()
Область интегрирования
представляет собой четверть круга, т.е.
определяется условиями
![]()
Следовательно,
Список использованной
литературы.
-
А.Ф. Бермант ,И.Г.
Араманович
Краткий курс
математического анализа для втузов:
Учебное пособие для втузов: – М.: Наука,
Главная редакция физико-математической
литературы , 1971 г.,736с.
-
Н.С. Пискунов
Дифференциальное
и интегральное исчисления для втузов,
Том 2:
Учебное пособие
для втузов.-13-е изд. -М. :Наука, Главная
редакция физико-математической
литературы, 1985.-560с.
-
В.С. Шипачёв
Высшая
математика: Учебное пособие для втузов:
– М: Наука,
Главная редакция
физико-математической литературы.
Соседние файлы в предмете Алгебра и геометрия
- #
- #
- #
Содержание:
- Двойной интеграл
- Двойной интеграл в прямоугольных декартовых координатах
- Двойной интеграл в полярных координатах
- Двойной интеграл в декартовых координатах. Определение, теорема существования
- Геометрический смысл двойного интеграла
- Свойства двойного интеграла
- Вычисление двойного интеграла в декартовых координатах
- Двойной интеграл в полярных координатах
- Вычисление площади плоской фигуры с помощью двойного интеграла
- Вычисление объема тела с помощью двойного интеграла
Двойной интеграл
В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл
На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным интегралом.
Задача.
Найти объем тела, ограниченного сверху непрерывной поверхностью  снизу конечной замкнутой областью
снизу конечной замкнутой областью плоскости
плоскости  и с боков прямой цилиндрической поверхностью, построенной на границе области
и с боков прямой цилиндрической поверхностью, построенной на границе области  и имеющей образующие, перпендикулярные плоскости
и имеющей образующие, перпендикулярные плоскости  (рис. 245).
(рис. 245).

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Тело указанного вида для краткости называется цилиндроидом. В частном случае, когда верхнее основание цилиндроида есть плоскость, параллельная нижнему основанию его, то цилиндроид называется цилиндром.
Примером цилиндра служит круговой цилиндр, рассматриваемый в средней школе.
Обобщая рассуждение, обычно применяемое для нахождения объема кругового цилиндра, нетрудно доказать, что объем  цилиндра с площадью основания
цилиндра с площадью основания  и высотой
и высотой  равен
равен 
Для вычисления объема  данного цилиндроида разобьем основание его
данного цилиндроида разобьем основание его  на конечное число элементарных ячеек
на конечное число элементарных ячеек  (вообще говоря, криволинейных). В каждой из этих ячеек
(вообще говоря, криволинейных). В каждой из этих ячеек  выберем точку
выберем точку  и построим прямой цилиндрический столбик с основанием
и построим прямой цилиндрический столбик с основанием  и высотой
и высотой 
 равной аппликате поверхности в выбранной точке.
равной аппликате поверхности в выбранной точке.
Объем такого столбика на основании формулы объема цилиндра, очевидно, равен

где  — площадь соответствующей ячейки. Сумма объемов этих цилиндрических столбиков представляет собой объем ступенчатого тела, приближенно заменяющего данное криволинейное тело, причем аппроксимация является, вообще говоря, тем более точной, чем меньше диаметры ячеек
— площадь соответствующей ячейки. Сумма объемов этих цилиндрических столбиков представляет собой объем ступенчатого тела, приближенно заменяющего данное криволинейное тело, причем аппроксимация является, вообще говоря, тем более точной, чем меньше диаметры ячеек Поэтому объем нашего цилиндроида приближенно выразится суммой
Поэтому объем нашего цилиндроида приближенно выразится суммой

Формула (2) дает возможность найти объем  с любой степенью точности, если число ячеек
с любой степенью точности, если число ячеек  достаточно велико и линейные размеры их весьма малы. Обозначим через
достаточно велико и линейные размеры их весьма малы. Обозначим через  диаметр ячейки
диаметр ячейки  , т. е. наибольший линейный размер ее. Точнее говоря, под диаметром
, т. е. наибольший линейный размер ее. Точнее говоря, под диаметром  ограниченной замкнутой (т. е. с присоединенной границей) фигуры
ограниченной замкнутой (т. е. с присоединенной границей) фигуры  (дуги, площадки и т. п.) понимается длина наибольшей ее хорды
(дуги, площадки и т. п.) понимается длина наибольшей ее хорды  где
где  (рис. 246)2)
(рис. 246)2) 
Из данного определения следует, что фигура  имеющая диаметр
имеющая диаметр  целиком помещается внутри круга радиуса
целиком помещается внутри круга радиуса  описанного из любой ее точки
описанного из любой ее точки  как из центра. Поэтому если
как из центра. Поэтому если  то фигура
то фигура  «стягивается в точку». Аналогично определяется диаметр пространственного тела.
«стягивается в точку». Аналогично определяется диаметр пространственного тела.
Пусть  — наибольший из диаметров ячеек
— наибольший из диаметров ячеек 
 Предполагая, что в формуле (2) число ячеек
Предполагая, что в формуле (2) число ячеек  неограниченно возрастает
неограниченно возрастает  причем диаметр наибольшей из них становится сколь угодно малым
причем диаметр наибольшей из них становится сколь угодно малым  в пределе получаем точную формулу для объема цилиндроида
в пределе получаем точную формулу для объема цилиндроида 
Выражение, стоящее в правой части формулы (3), называется двойным интегралом от функции  распространенным на область
распространенным на область  и обозначается следующим образом:
и обозначается следующим образом: 
Поэтому для объема цилиндроида окончательно имеем

Обобщая конструкцию, примененную для вычисления объема цилиндроида, приходим к следующим определениям.
Возможно вам будут полезны данные страницы:
Опрелеление 1. Двумерной интегральной суммой (2) от данной функции  распространенной на данную область
распространенной на данную область  называется сумма парных произведений площадей элементарных ячеек
называется сумма парных произведений площадей элементарных ячеек  области
области  назначения
назначения  функции
функции  в выделенных точках этих ячеек (рис. 247).
в выделенных точках этих ячеек (рис. 247). 
Опрелеление 2. Двойным интегралом (4) от функции  распространенным на данную область
распространенным на данную область  называется предел соответствующей двумерной интегральной суммы (2) при неограниченном возрастании числа
называется предел соответствующей двумерной интегральной суммы (2) при неограниченном возрастании числа  элементарных ячеек
элементарных ячеек  и стремлении к нулю их наибольшего диаметра
и стремлении к нулю их наибольшего диаметра  при условии, что этот предел существует и не зависит от способа дробления области
при условии, что этот предел существует и не зависит от способа дробления области  на элементарные ячейки
на элементарные ячейки  и выбора точек в них. В формуле (4)
и выбора точек в них. В формуле (4)  называется подынтегральной функцией,
называется подынтегральной функцией,  — областью интегрирования, а
— областью интегрирования, а  — элементом площади.
— элементом площади.
Справедлива следующая теорема:
ТЕОРЕМА. Если область  с кусочно-гладкой границей
с кусочно-гладкой границей  ограничена и замкнута
ограничена и замкнута  а функция
а функция  непрерывна в области
непрерывна в области  то двойной интеграл
то двойной интеграл  существует, т. е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа дробления области
существует, т. е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа дробления области  на элементарные ячейки
на элементарные ячейки  и выбора точек в них.
и выбора точек в них.
В дальнейшем мы будем предполагать, что условия этой теоремы выполнены.
В формуле (6) нет необходимости указывать, что  так как из
так как из  очевидно, следует
очевидно, следует 
Если  то двойной интеграл (6) представляет собой объем прямого цилиндроида, построенного на области
то двойной интеграл (6) представляет собой объем прямого цилиндроида, построенного на области  как на основании и ограниченного сверху поверхностью
как на основании и ограниченного сверху поверхностью  (геометрический смысл двойного интеграла).
(геометрический смысл двойного интеграла).
Так как значение двойного интеграла не зависит от вида элементарных ячеек, то в дальнейшем при решении задач мы будем использовать это обстоятельство, выбирая наиболее подходящие сетки. Весьма часто удобной оказывается прямоугольная сетка, образованная пересечением двух систем прямых, параллельных соответственно координатным осям  и
и  (рис. 248).
(рис. 248).
В этом случае элементарными ячейками  являются прямоугольники со сторонами, равными
являются прямоугольники со сторонами, равными  и
и  за исключением, возможно, ячеек, примыкающих к границе
за исключением, возможно, ячеек, примыкающих к границе  Чтобы подчеркнуть использование прямоугольной сетки, в обозначении интеграла (4) полагают
Чтобы подчеркнуть использование прямоугольной сетки, в обозначении интеграла (4) полагают  (двумерный элемент площади в прямоугольных координатах), причем
(двумерный элемент площади в прямоугольных координатах), причем  где
где  и сумма (8) распространяется на все значения
и сумма (8) распространяется на все значения  и
и  для которых
для которых  (можно показать, что непрямоугольные ячейки, примыкающие к кусочно-гладкой границе
(можно показать, что непрямоугольные ячейки, примыкающие к кусочно-гладкой границе  не влияют на значение предела (8)).
не влияют на значение предела (8)).
В следующих параграфах мы рассмотрим основные способы вычисления двойного интеграла.

Примеры с решением
Пример 1.
Найти
 где
где  — квадрат
— квадрат 
Расставляя пределы интегрирования, будем иметь  Геометрически
Геометрически  представляет собой объем цилиндроида с квадратным нижним основанием, ограниченного сверху параболоидом вращения
представляет собой объем цилиндроида с квадратным нижним основанием, ограниченного сверху параболоидом вращения  (рис. 254).
(рис. 254).

Пример 2.
Вычислить двойной интеграл

где  — прямоугольник
— прямоугольник 
Расставляя пределы интегрирования и разделяя переменные, будем иметь 
Пример 3.
Вычислить  где
где  — треугольник с вершинами
— треугольник с вершинами  (рис. 255).
(рис. 255).

Область  ограничена прямыми
ограничена прямыми  2 и является стандартной как относительно оси
2 и является стандартной как относительно оси  так и оси
так и оси 
Для вертикали 
 точка входа
точка входа в область
в область  есть
есть  «точка выхода» —
«точка выхода» —  Таким образом, при фиксированном
Таким образом, при фиксированном  переменная
переменная  для точек области
для точек области  меняется от
меняется от  до
до  Поэтому, интегрируя в двойном интеграле (10) сначала по
Поэтому, интегрируя в двойном интеграле (10) сначала по  при
при 
 а затем по
а затем по  согласно формуле (5) будем иметь
согласно формуле (5) будем иметь 
Аналогично, для горизонтали  «точка входа» в область есть
«точка входа» в область есть  и «точка выхода» —
и «точка выхода» —  Следовательно, при фиксированном
Следовательно, при фиксированном  переменная
переменная  для точек области
для точек области  меняется от
меняется от  до
до  Произведя в двойном интеграле (10) интегрирование сначала по
Произведя в двойном интеграле (10) интегрирование сначала по  при
при  а затем по
а затем по  на основании формулы (9) получаем
на основании формулы (9) получаем 
Мы пришли, как и следовало ожидать, к тому же самому результату, причем второй способ вычисления оказался несколько более сложным.
Пример 4.
Изменить порядок интегрирования в повторном интеграле

Область интегрирования  ограничена кривыми
ограничена кривыми  (рис. 256). Отсюда, изменяя роли осей координат, получаем
(рис. 256). Отсюда, изменяя роли осей координат, получаем

Следовательно, 
Пример 5.
Расставить пределы интегрирования в двойном интеграле  если область интегрирования
если область интегрирования  есть круговое кольцо, ограниченное окружностями
есть круговое кольцо, ограниченное окружностями 
 (рис. 257). Область
(рис. 257). Область  не является стандартной. Для расстановки пределов интегрирования в интервале (13) разбиваем область
не является стандартной. Для расстановки пределов интегрирования в интервале (13) разбиваем область  на четыре стандартные относительно оси
на четыре стандартные относительно оси  области
области  как указано на рисунке. Используя уравнение окружностей
как указано на рисунке. Используя уравнение окружностей 

имеем

Аналогичная формула получится, если мы будем расставлять пределы интегрирования в другом порядке.
Двойной интеграл в прямоугольных декартовых координатах
Предположим для определенности, что область интегрирования  представляет собой криволинейную трапецию (рис. 249)
представляет собой криволинейную трапецию (рис. 249) 

где  — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке  Такую область будем называть стандартной относительно оси
Такую область будем называть стандартной относительно оси  Заметим, что вертикаль, проходящая через точку
Заметим, что вертикаль, проходящая через точку  оси
оси  при
при  пересекает границу
пересекает границу  области
области только в двух точках
только в двух точках  («точка входа») и
(«точка входа») и  («точка выхода»).
(«точка выхода»).
Пусть  — функция, непрерывная в области
— функция, непрерывная в области  и =
и =  — ее двойной интеграл.
— ее двойной интеграл.
1) Предположим сначала, что  в области
в области  Тогда двойной интеграл
Тогда двойной интеграл  представляет собой объем цилиндроида (рис. 250), ограниченного снизу областью
представляет собой объем цилиндроида (рис. 250), ограниченного снизу областью  сверху поверхностью
сверху поверхностью  и с боков прямой цилиндрической поверхностью
и с боков прямой цилиндрической поверхностью

Для вычисления объема  применим метод сечений (гл. XV, § 5). А именно, пусть
применим метод сечений (гл. XV, § 5). А именно, пусть  — площадь сечения цилиндроида плоскостью
— площадь сечения цилиндроида плоскостью  перпендикулярной оси
перпендикулярной оси  в точке ее
в точке ее  (рис. 250).
(рис. 250).
Тогда имеем 
Но  представляет собой площадь криволинейной трапеции, ограниченной снизу отрезком
представляет собой площадь криволинейной трапеции, ограниченной снизу отрезком  и сверху кривой
и сверху кривой 
Поэтому 
Можно доказать, что при наших условиях  непрерывна при
непрерывна при 
Подставляя выражение (4) в формулу (3), получим окончательно 
Таким образом, двойной интеграл равен соответствующему повторному интегралу (5), т. е. вычисление двойного интеграла сводится к двум квадратурам. Заметим, что при вычислении внутреннего интеграла в формуле (5)  рассматривается как постоянная величина.
рассматривается как постоянная величина.
2) В случае знакопеременной функции  например, если
например, если  при
при  и
и  при
при  двойной интеграл (2) равен алгебраической сумме объемов
двойной интеграл (2) равен алгебраической сумме объемов  цилиндроидов, построенных соответственно на основаниях
цилиндроидов, построенных соответственно на основаниях  (pиc. 251),
(pиc. 251),

т. е.  Можно доказать, что формула (5) справедлива и в этом случае.
Можно доказать, что формула (5) справедлива и в этом случае.
Отметим один важный случай: пусть  — прямоугольник
— прямоугольник  (рис. 252) и
(рис. 252) и  где
где  — функция, непрерывная на
— функция, непрерывная на  и зависящая только от
и зависящая только от  и
и  — функция, непрерывная на
— функция, непрерывная на  и зависящая только от
и зависящая только от 
В силу формулы (5) имеем 
Но внутренний интеграл в формуле (7) есть постоянное число, поэтому его можно вынести за знак внешнего интеграла и мы получим 
т. е. двойной интеграл (8) равен произведению двух однократных интегралов.
Замечание 1. Если область — стандартная относительно оси
— стандартная относительно оси  (рис. 253)
(рис. 253)  то по аналогии с формулой (5) получаем
то по аналогии с формулой (5) получаем 
В частности, если область  есть прямоугольник: a
есть прямоугольник: a 
 есть прямоугольник: a то имеем
есть прямоугольник: a то имеем 

Отсюда получаем 
т е. если пределы интегрирования в повторном интеграле от непрерывной функции конечны и постоянны, то результат интегрирования не зависит от порядка интегрирования.
Двойной интеграл в полярных координатах
Пусть в двойном интеграле
при обычных предположениях мы желаем перейти к полярным координатам  и
и  , полагая
, полагая

Область интегрирования  разобьем на элементарные ячейки
разобьем на элементарные ячейки  с помощью координатных линий
с помощью координатных линий  (окружности) и
(окружности) и  =
=  (лучи) (рис. 258).
(лучи) (рис. 258). 
Введем обозначения  Так как окружность перпендикулярна (ортогональна) радиусам, то внутренние ячейки
Так как окружность перпендикулярна (ортогональна) радиусам, то внутренние ячейки  с точностью до бесконечно малых высшего порядка малости относительно их площади можно рассматривать как прямоугольники с измерениями
с точностью до бесконечно малых высшего порядка малости относительно их площади можно рассматривать как прямоугольники с измерениями  поэтому площадь каждой такой ячейки будет равна
поэтому площадь каждой такой ячейки будет равна 
Что касается ячеек  неправильной формы, примыкающих к границе
неправильной формы, примыкающих к границе  области интегрирования
области интегрирования  то эти ячейки не повлияют на значение двойного интеграла (ср. § 1, формула (8)) и мы их будем игнорировать.
то эти ячейки не повлияют на значение двойного интеграла (ср. § 1, формула (8)) и мы их будем игнорировать.
В качестве точки  для простоты выберем вершину ячейки
для простоты выберем вершину ячейки  с полярными координатами
с полярными координатами  и
и  Тогда декартовы координаты точки
Тогда декартовы координаты точки  равны
равны

и, следовательно, 
Двойной интеграл (1) представляет собой предел двумерной интегральной суммы, причем можно показать, что на значение этого предела не влияют добавки к слагаемым интегральной суммы, являющиеся бесконечно малыми высшего порядка малости. Поэтому, учитывая формулы (3) и (3′)» получаем 
где  — максимальный диаметр ячеек
— максимальный диаметр ячеек  и сумма распространена на все ячейки указанного выше вида, целиком содержащиеся в области
и сумма распространена на все ячейки указанного выше вида, целиком содержащиеся в области 
С другой стороны, величины  и
и  суть числа и их можно рассматривать как прямоугольные декартовы координаты некоторых точек плоскости
суть числа и их можно рассматривать как прямоугольные декартовы координаты некоторых точек плоскости  Таким образом, сумма (4) является интегральной суммой для функции
Таким образом, сумма (4) является интегральной суммой для функции

соответствующая прямоугольной сетке с линейными элементами  и
и  Следовательно,
Следовательно, 

Выравнивая формулы (4) и (5), получаем окончательно 
Выражение  называется двумерным элементом площади в полярных координатах (ср. гл. XV, § 2).
называется двумерным элементом площади в полярных координатах (ср. гл. XV, § 2).
Итак, чтобы в двойном интеграле (1) перейти к полярным координатам, достаточно координаты  и
и  заменить по формулам (2), а вместо элемента площади
заменить по формулам (2), а вместо элемента площади  и подставить выражение (7).
и подставить выражение (7).
Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования  определяется неравенствами
определяется неравенствами 
где  — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке  (рис. 259) Тогда по аналогии с прямоугольными координатами (см. § 2) имеем
(рис. 259) Тогда по аналогии с прямоугольными координатами (см. § 2) имеем 
где 
Пример 6.
Переходя к полярным координатам  и
и  вычислить двойной интеграл
вычислить двойной интеграл  где
где  первая четверть круга радиуса
первая четверть круга радиуса  с центром в точке
с центром в точке  (рис. 260). Так как
(рис. 260). Так как  то , применяя формулу (6), получаем
то , применяя формулу (6), получаем

Область  определяется неравенствами
определяется неравенствами  Поэтому на основании формулы (8) имеем
Поэтому на основании формулы (8) имеем

Пример 7.
В интеграле
 перейти к полярным координатам.
перейти к полярным координатам.
Область интегрирования здесь есть треугольник. ограниченный прямыми
ограниченный прямыми  (рис. 261).
(рис. 261).

В полярных координатах уравнения этих прямых записываются следующим образом:  и, следовательно, область
и, следовательно, область определяется неравенствами
определяется неравенствами  Отсюда на основании формул (6) и (8), учитывая, что
Отсюда на основании формул (6) и (8), учитывая, что  имеем
имеем 
Двойной интеграл в декартовых координатах. Определение, теорема существования
Понятие «двойной интеграл» является естественным обобщением понятия «определенный интеграл» на случай функции двух переменных. Поэтому его определение принципиально не отличается от определения определенного интеграла и вводится аналогичным образом.
Пусть функция  или
или  где
где  определена и непрерывна в замкнутой области
определена и непрерывна в замкнутой области  плоскости
плоскости  то есть на множестве точек координатной плоскости, ограниченная сомкнуты линией (или линиями)
то есть на множестве точек координатной плоскости, ограниченная сомкнуты линией (или линиями)  , с учетом точек линии
, с учетом точек линии  – пределы области.
– пределы области.
Выполним такую (стандартную) процедуру:
1) разобьем область  произвольным образом какими-либо линиями на n частичных областей с площадями
произвольным образом какими-либо линиями на n частичных областей с площадями  (или просто – на
(или просто – на  плоскостей
плоскостей  (рис. 26.1) и самую большую из расстояний между двумя точками границы плоскости назовем диаметром плоскости
(рис. 26.1) и самую большую из расстояний между двумя точками границы плоскости назовем диаметром плоскости  а максимальный среди них
а максимальный среди них  – диаметром разбиения области
– диаметром разбиения области 
2) выберем на каждой из плоскостей произвольным образом по точке 
 вычислим
вычислим  и найдем произведения
и найдем произведения 
3) составим сумму всех таких произведений

которую назовем интегральной суммой для функции  в области
в области 
4) вычислим границу (если она существует) интегральной суммы (26.1) при условии, что диаметр разбиения стремится к нулю при неограниченном росте  то есть
то есть вместе с
вместе с 

Рис. 26.1
Конечна граница  интегральной суммы
интегральной суммы  когда диаметр разбиения стремится к нулю
когда диаметр разбиения стремится к нулю  а
а  называется двойным интегралом (от) функции
называется двойным интегралом (от) функции  по области
по области  и обозначается так:
и обозначается так:
 или
или 
где  – знак (символ) двойного интеграла;
– знак (символ) двойного интеграла;
 – область интегрирования;
– область интегрирования;
 – подынтегральная функция;
– подынтегральная функция;
 – подынтегральное выражение;
– подынтегральное выражение;
 – переменные интегрирования;
– переменные интегрирования;
 – элемент площади, или дифференциал площади.
– элемент площади, или дифференциал площади.
Следовательно, по определению

Теорема 26.1 (существование двойного интеграла). Если задана функция двух переменных непрерывна в рассматриваемой замкнутой области, то существует конечное предел интегральной суммы (то есть двойной интеграл), и она не зависит ни от способа разбиения области на плоскости, ни от выбора точек в них для составления интегральной суммы.
Теорему приводим без доказательства.
Функция  для которой существует двойной интеграл по области
для которой существует двойной интеграл по области  называется интегрируемой на этой области.
называется интегрируемой на этой области.
Согласно теореме 26.1 разбиения области  можно осуществлять простым из возможных способов (рис. 26.2), а именно: в декартовой системе координат
можно осуществлять простым из возможных способов (рис. 26.2), а именно: в декартовой системе координат  – прямыми, параллельными координатным осям.
– прямыми, параллельными координатным осям.

Рис. 26.2
В этом случае плоскость – прямоугольник со сторонами  который образуется при переходе от точки
который образуется при переходе от точки  к точке
к точке  где
где  Поэтому
Поэтому  потому приросты независимых переменных
потому приросты независимых переменных  равны их дифференциалам:
равны их дифференциалам: 
Таким образом, можно записать:

Геометрический смысл двойного интеграла
В дальнейшем тело, ограниченное поверхностью  плоскостью
плоскостью  и цилиндрической поверхностью, образующая которой параллельна оси
и цилиндрической поверхностью, образующая которой параллельна оси  а направляющей предел
а направляющей предел  области
области  (рис. 26.3), коротко будем называть цилиндрическим телом для функции
(рис. 26.3), коротко будем называть цилиндрическим телом для функции  на (области)
на (области) 
Анализируя с геометрической точки зрения процедуру, которая предшествовала определению двойного интеграла для неотъемлемой в области  функции
функции  приходим к выводу: каждое слагаемое
приходим к выводу: каждое слагаемое интегральной суммы численно равен объему прямой призмы с площадью основания
интегральной суммы численно равен объему прямой призмы с площадью основания  и высотой
и высотой  (рис. 26.3), а интегральная сумма численно дает приближенное значение
(рис. 26.3), а интегральная сумма численно дает приближенное значение  объема
объема  цилиндрического тела для функции
цилиндрического тела для функции  на области
на области 


Рис. 26.3
Свойства двойного интеграла
Сравнивая определение двойного интеграла и определение определенного интеграла функции одной переменной, можно сделать вывод, что по структуре эти определения аналогичны. Поэтому свойства двойного интеграла, а также их доведения почти повторяют соответствующие свойства определенного интеграла. Приведем эти свойства.
1. Двойной интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме двойных интегралов от слагаемых:

2. Постоянный множитель можно выносить за знак двойного интеграла:

3. Если область  разбить на две области
разбить на две области  и
и  которые не имеют общих внутренних точек, и функция
которые не имеют общих внутренних точек, и функция  непрерывна в области
непрерывна в области  то
то

4. Если  в области
в области  то
то

5. Если в каждой точке области  функции
функции  и
и  непрерывны и удовлетворяют условию
непрерывны и удовлетворяют условию  то
то

6. Если функция  непрерывна в области
непрерывна в области  и удовлетворяет двойное неравенство
и удовлетворяет двойное неравенство  где
где  и
и  – наименьшее и наибольшее значение функции
– наименьшее и наибольшее значение функции  в области
в области  , то
, то

где  – площадь области
– площадь области 
7. Если функция  непрерывна в области
непрерывна в области  то в этой области существует такая точка
то в этой области существует такая точка  что
что

где  – площадь области
– площадь области 
Значение  называется средним значением функции
называется средним значением функции  в области
в области 
Вычисление двойного интеграла в декартовых координатах
Установим формулы для вычисления двойного интеграла  опираясь на его геометрический смысл (26.3) и формулу вычисления объема тела с помощью определенного интеграла:
опираясь на его геометрический смысл (26.3) и формулу вычисления объема тела с помощью определенного интеграла:  (26.11) где
(26.11) где  – площадь поперечного сечения тела плоскостью, перпендикулярной к оси
– площадь поперечного сечения тела плоскостью, перпендикулярной к оси  а
а  и
и  = – уравнение плоскостей, ограничивающих данное тело.
= – уравнение плоскостей, ограничивающих данное тело.
Область  плоскости
плоскости  называется правильной, или простой, в направлении оси
называется правильной, или простой, в направлении оси  если она ограничена прямыми
если она ограничена прямыми  и двумя непрерывными кривыми
и двумя непрерывными кривыми  и
и  а любая прямая
а любая прямая  параллельная оси
параллельная оси  пересекает каждую из этих кривых только в одной точке (рис. 26.4 а, б).
пересекает каждую из этих кривых только в одной точке (рис. 26.4 а, б).

Рис. 26.4
Рассмотрим цилиндрическое тело для функции  на правильной в направлении оси
на правильной в направлении оси  области
области  (рис. 26.5). Проведем произвольную плоскость, параллельную плоскости
(рис. 26.5). Проведем произвольную плоскость, параллельную плоскости  В сечении цилиндрического тела этой плоскостью получаем криволинейную трапецию, площадь которой выражается интегралом от функции
В сечении цилиндрического тела этой плоскостью получаем криволинейную трапецию, площадь которой выражается интегралом от функции  где
где  фиксировано, а
фиксировано, а  меняется от
меняется от  Таким образом, площадь сечения равна:
Таким образом, площадь сечения равна:

Согласно формуле (26.11) объем данного цилиндрического тела равна:


Рис. 26.5
С другой стороны, на основании геометрического смысла двойного интеграла имеем:

Сопоставляя последние две формулы, окончательно получаем:

или в более удобной (для использования) форме:

Правую часть формулы (26.12) как определенный интеграл от определенного интеграла называют двукратным или повторным интегралом от функции  по области
по области  В нем интеграл по переменной y называют внутренним, а по переменной
В нем интеграл по переменной y называют внутренним, а по переменной  – внешним интегралом
– внешним интегралом
Согласно формуле (26.12) сначала проводят интегрирования по переменной  то есть находят внутренний интеграл
то есть находят внутренний интеграл  (при этом переменная
(при этом переменная  считается постоянной), после чего полученную функцию от
считается постоянной), после чего полученную функцию от  интегрируют в пределах от
интегрируют в пределах от  до
до  с переменной
с переменной  то есть вычисляют внешний интеграл.
то есть вычисляют внешний интеграл.
Аналогично область  плоскости
плоскости  называется правильной, или простой, в направлении оси
называется правильной, или простой, в направлении оси  если она ограничена прямыми
если она ограничена прямыми  и
и 
 и двумя непрерывными кривыми
и двумя непрерывными кривыми  и
и  а любая прямая
а любая прямая 
 , параллельная оси
, параллельная оси  пересекает каждую из этих кривых только в одной точке (рис.26.6 а, б).
пересекает каждую из этих кривых только в одной точке (рис.26.6 а, б).

Рис. 26.6
Для правильной в направлении оси  области вычисления двойного интеграла сводится к вычислению двукратного или повторного, интеграла по формуле:
области вычисления двойного интеграла сводится к вычислению двукратного или повторного, интеграла по формуле:

Как итог рассматриваемого наведем порядок нахождения двойного интеграла:
1) строим область интегрирования  ограниченную заданными линиями;
ограниченную заданными линиями;
2) анализируем ее с целью установления того, является ли она правильной в направлении хотя бы одной из осей координат, и определяем границы интегрирования;
3) применяем одну из формул, (26.12) или (26.13), и находим сначала внутренний интеграл (как правило, со сменными пределами интегрирования), а затем – внешний (с постоянными пределами интегрирования).

Рис. 26.7
Если область  не является правильной, то ее подают в виде объединения правильных областей, осуществив ее разбиение на части прямыми, параллельными координатным осям, и применяют свойство 3 двойного интеграла, а именно:
не является правильной, то ее подают в виде объединения правильных областей, осуществив ее разбиение на части прямыми, параллельными координатным осям, и применяют свойство 3 двойного интеграла, а именно:

Формулы приведения двойного интеграла к повторным (26.12) и (26.13) существенно упрощаются, если область  является прямоугольником со сторонами, параллельными осям координат (рис. 26.7).
является прямоугольником со сторонами, параллельными осям координат (рис. 26.7).
В этом случае пределы интегрирования являются постоянными не только для внешнего, но и для внутреннего интеграла:

и в каком порядке интегрировать сначала по переменной  а затем по переменной
а затем по переменной  или наоборот, не имеет значения.
или наоборот, не имеет значения.
Вычислим  если область
если область  – прямоугольник:
– прямоугольник: 

По формуле (26.15) имеем:

Если подынтегральная функция является произведением функции от  с функцией от
с функцией от  и пределы интегрирования постоянные, то двойной интеграл равен произведению определенных интегралов по каждой переменной.
и пределы интегрирования постоянные, то двойной интеграл равен произведению определенных интегралов по каждой переменной.
Вычислим  если область
если область  ограничена линиями:
ограничена линиями: 
 и
и 
Построим область интегрирования  (рис. 26.8). Она является правильным в направлении оси
(рис. 26.8). Она является правильным в направлении оси  поэтому внутреннее интегрирование проводим по переменной
поэтому внутреннее интегрирование проводим по переменной  а внешнее – по
а внешнее – по 


Рис. 26.8
Вычислим  если область
если область  ограничена линиями:
ограничена линиями:
 и
и 
Построим область  (рис. 26.9).
(рис. 26.9).

Рис. 26.9
Она является правильной в направлении оси  поэтому внутреннее интегрирование проводим по переменной
поэтому внутреннее интегрирование проводим по переменной  а внешнее – по
а внешнее – по 

Вычислим  если область
если область  ограничена линиями:
ограничена линиями:
 и
и 
Построим область  (рис. 26.10).
(рис. 26.10).
Находим точки взаимного пересечения каждой пары линий, ограничивающих  .
.
Линии  – пересекаются в начале координат
– пересекаются в начале координат 


Рис. 26.10
Область  не является правильным ни в направлении оси
не является правильным ни в направлении оси  ни в направлении оси
ни в направлении оси  Разобьем ее прямой
Разобьем ее прямой  на две правильные в направлении оси
на две правильные в направлении оси  области
области  и
и  По формуле (26.14) имеем:
По формуле (26.14) имеем:

Двойной интеграл в полярных координатах
При переходе в двойном интеграле от декартовых координат  и
и  к полярным
к полярным  и
и  используют связь между координатами
используют связь между координатами  и
и  (24.4):
(24.4):

и выражение для дифференциала площади в полярных координатах:

Соответствующая формула перехода имеет вид:

где  и
и  – полярные координаты точек области
– полярные координаты точек области 
Вычисление двойного интеграла в полярных координатах сводится к вычислению двукратного (повторного) интеграла по переменными  и
и  .
.
Если область  является разностью двух криволинейных секторов (рис. 26.11), то есть фигурой, ограниченной лучами, которые образуют с полярной осью
является разностью двух криволинейных секторов (рис. 26.11), то есть фигурой, ограниченной лучами, которые образуют с полярной осью  углы
углы  и
и  и кривыми
и кривыми  и
и  где
где 
 то
то


Рис. 26.11
Если область  ограничена сомкнутой линией
ограничена сомкнутой линией  и начало координат лежит внутри области, то
и начало координат лежит внутри области, то

Переход к полярным координатам в двойном интеграле целесообразно делать, если область интегрирования представляет собой круг, кольцо или их частями, то есть граница области  содержит дуги кругов и отрезки лучей, исходящих из полюса
содержит дуги кругов и отрезки лучей, исходящих из полюса 
Вычислим  где
где  – круг
– круг 
Пределом области  является окружность радиуса 2 с центром в точке
является окружность радиуса 2 с центром в точке 

Применим формулы перехода от декартовых координат к полярным:

В координатах  уравнение границы области
уравнение границы области  примет вид:
примет вид:

Построим в декартовых координатах круг  или
или  (рис. 26.12). В полярных координатах соответствующая область интегрирования – криволинейный сектор, ограниченный лучами
(рис. 26.12). В полярных координатах соответствующая область интегрирования – криволинейный сектор, ограниченный лучами  а полярный радиус
а полярный радиус  меняется от
меняется от  до
до 

Рис. 26.12
По формуле (26.17) имеем:

Вычислим с помощью двойного интеграла в полярных координатах несобственный интеграл Эйлера-Пуассона:

Для этого рассмотрим двойной интеграл  где
где  – четверть круга некоторого радиуса
– четверть круга некоторого радиуса  расположенного в первом квадранте декартовой системы координат:
расположенного в первом квадранте декартовой системы координат:  Для вычисления
Для вычисления  перейдем к полярным координатам:
перейдем к полярным координатам: 
 тогда
тогда

Если теперь неограниченно увеличивать радиус  то получим несобственный интеграл по всей первой четверти (рис. 26.13), так как при
то получим несобственный интеграл по всей первой четверти (рис. 26.13), так как при  область
область 

Рис. 26.13
расширяется так, что любая точка первой четверти  попадет в
попадет в  и останется в ней, а
и останется в ней, а  направляться в
направляться в 

С другой стороны, при  и
и  и
и  поэтому можно записать:
поэтому можно записать:

поскольку определенный интеграл (а с ним и несобственный) не зависит от обозначения переменной интегрирования.
Таким образом,  откуда:
откуда: 
Вычисление площади плоской фигуры с помощью двойного интеграла
Если в формуле (26.3):  положить
положить 
 то интегральная сумма для функции
то интегральная сумма для функции  в области
в области  давать приближенно площадь этой области
давать приближенно площадь этой области 

а за ее точное значение принимается значение интеграла:

Если область  – разность двух криволинейных секторов (рис. 26.11) – заданная в полярной системе координат неровностями
– разность двух криволинейных секторов (рис. 26.11) – заданная в полярной системе координат неровностями
 то
то

Найдем площадь фигуры, ограниченной линиями: 
Построим плоскую фигуру (рис. 26.14) и определим точки пересечения заданных линий – гиперболы и прямой, – решив систему их уравнений:


Рис. 26.14
Решим первое уравнение: 
 откуда
откуда 
 тогда
тогда 
 Следующим образом:
Следующим образом:  . (Вторая ветвь гиперболы
. (Вторая ветвь гиперболы  не показаны, поскольку она не имеет общих точек с прямой
не показаны, поскольку она не имеет общих точек с прямой 
Заданная фигура является областью, правильной и в направлении оси  и в направлении оси
и в направлении оси  Для вычисления ее площади воспользуемся формулой (26.19). В соответствующем повторном интеграле внешний интеграл берем по переменной
Для вычисления ее площади воспользуемся формулой (26.19). В соответствующем повторном интеграле внешний интеграл берем по переменной  от
от  до
до  а внутренний – по переменной
а внутренний – по переменной  от
от  к
к 

Вычислим площадь плоской области  ограниченной кругом
ограниченной кругом  и прямыми
и прямыми 
Построим область  для чего предварительно сведем уравнение окружности
для чего предварительно сведем уравнение окружности  к каноническому виду
к каноническому виду  (рис. 26.15).
(рис. 26.15).
Площадь заданной области целесообразно вычислить в полярных координатах:
 Запишем уравнение окружности
Запишем уравнение окружности 
 в координатах
в координатах  или
или  По уравнениям заданных прямых устанавливаем, что угол
По уравнениям заданных прямых устанавливаем, что угол  изменяется от
изменяется от  до
до  Таким образом, согласно формуле (26.20) имеем:
Таким образом, согласно формуле (26.20) имеем:

Вычисление объема тела с помощью двойного интеграла
По определению двойного интеграла и его геометрическим смыслом было доказано, что двойной интеграл  равен объему тела, ограниченного поверхностью
равен объему тела, ограниченного поверхностью  областью
областью  плоскости
плоскости  и цилиндрической поверхностью, направляющей которой является граница области
и цилиндрической поверхностью, направляющей которой является граница области  и образующими, параллельными оси
и образующими, параллельными оси  а именно:
а именно:

Найдем объем тела, ограниченного поверхностями: 


Проанализируем уравнение поверхностей и построим область интегрирования  Заданное пространственное тело ограничено: сверху – плоскостью
Заданное пространственное тело ограничено: сверху – плоскостью  боков – двумя параболическими цилиндрами
боков – двумя параболическими цилиндрами  и
и  с образующими, параллельными оси
с образующими, параллельными оси  снизу – областью
снизу – областью  которая «вырезается» на плоскости
которая «вырезается» на плоскости  цилиндрическими поверхностями и плоскостью
цилиндрическими поверхностями и плоскостью  (рис. 26.16).
(рис. 26.16).

Рис. 26.16
По формуле (26.3) получаем:

Найдем объем тела, ограниченного параболоидом  и плоскостями
и плоскостями 
 (в I октанте).
(в I октанте).
Построим область интегрирования  согласно условию задачи (рис. 26.17).
согласно условию задачи (рис. 26.17).
Вычислим объем  осуществив в двойном интеграле переход к полярным координатам, при этом уравнение окружности
осуществив в двойном интеграле переход к полярным координатам, при этом уравнение окружности  запишется как
запишется как  а прямые
а прямые  и
и  образуют с осью
образуют с осью  углы
углы  и
и  в соответствии.
в соответствии.

Рис. 26.17
Итак, по формуле (26.17) получим:

Рассмотрим две задачи, в которых двойной интеграл применяется для вычислений в сфере экономики.
1. Пусть  – областьь посевов некоторой сельскохозяйственной культуры. В каждой точке
– областьь посевов некоторой сельскохозяйственной культуры. В каждой точке  известна урожайность
известна урожайность  этой культуры (например, по наблюдениям из космоса). Тогда величина
этой культуры (например, по наблюдениям из космоса). Тогда величина  численно равна урожая, который можно собрать с области
численно равна урожая, который можно собрать с области  при отсутствии потерь.
при отсутствии потерь.
2. Аналогично, если функция  описывает плотность населения в точке
описывает плотность населения в точке  некоторого региона-области
некоторого региона-области  то величина
то величина  численно равна численности населения этого региона.
численно равна численности населения этого региона.
В обоих задачах аналитическое выражение подынтегральной функции устанавливается как эмпирическая формула.
Подводя итоги темы «двойной интеграл», отметим, что рядом с двойными существуют также и многомерные ( -мерные,
-мерные,  ) интегралы. Определение соответствующих интегралов вводятся аналогично тому, как это было сделано при определении двойного интеграла, а их вычисления сводится к вычислению
) интегралы. Определение соответствующих интегралов вводятся аналогично тому, как это было сделано при определении двойного интеграла, а их вычисления сводится к вычислению  -кратных определенных интегралов. Наиболее распространенными являются тройные интегралы от функции
-кратных определенных интегралов. Наиболее распространенными являются тройные интегралы от функции  по пространственной (трехмерной) области
по пространственной (трехмерной) области  ограниченной некоторой замкнутой поверхностью. Взятие тройного интеграла сводится к последовательному вычисления трех определенных интегралов.
ограниченной некоторой замкнутой поверхностью. Взятие тройного интеграла сводится к последовательному вычисления трех определенных интегралов.


Лекции:
- Асимптотическое поведение функций. Сравнение бесконечно малых функций
- Прямая линия на плоскости
- Выпуклость и вогнутость графика функции
- Матанализ для чайников
- Производные некоторых элементарных функций
- Система показательных уравнений
- Поверхность второго порядка
- Уравнения с одной переменной
- Найдите координаты точки пересечения графиков
- Геометрический смысл производной в точке
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
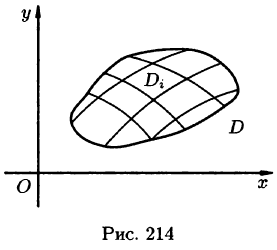
Пусть в замкнутой облас ти D плоскости Оху задана непрерывная функция z = f(x;y). Разобьем область D на п «элементарных областей»
ти D плоскости Оху задана непрерывная функция z = f(x;y). Разобьем область D на п «элементарных областей»  площади которых обозначим через
площади которых обозначим через  а диаметры (наибольшее расстояние между точками области) — через
а диаметры (наибольшее расстояние между точками области) — через  (см. рис. 214).
(см. рис. 214).
В каждой области  выберем произвольную точку
выберем произвольную точку  умножим значение
умножим значение 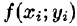 функции в этой точке на
функции в этой точке на 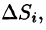 и составим сумму всех таких произведений:
и составим сумму всех таких произведений:
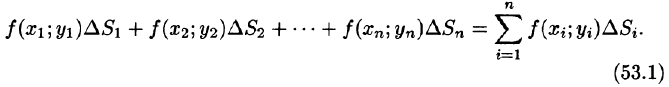
Эта сумма называется интегральной суммой функции f(x; у) в области D.
Рассмотрим предел интегральной суммы (53.1), когда п стремится к бесконечности таким образом, что 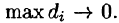 Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается
Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается
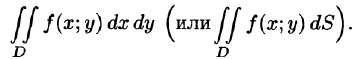
Таким образом, двойной интеграл определяется равенством
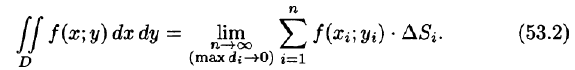
В этом случае функция f(x;y) называется интегрируемой в области D; D — область интегрирования; х и у — переменные интегрирования; dx dy (или dS) — элемент площади.
Для всякой ли функции f(x; у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.
Теорема:
Достаточное условие интегрируемости функции. Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания:
- Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
- Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллельными координатным осям (см. рис. 215). При этом
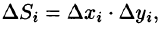 равенство (53.2) можно записать в виде
равенство (53.2) можно записать в виде
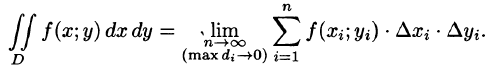
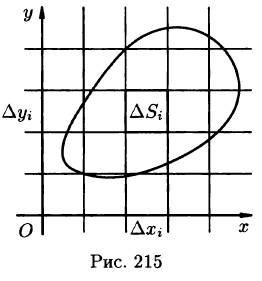

Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу. Объем цилиндрического тела
Рассмотрим тело, ограниченное сверху поверхностью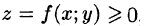 , снизу — замкнутой областью D плоскости Оху, с боков — цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 216). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z = f(x; у) на плоскость Оху) произвольным образом на п областей
, снизу — замкнутой областью D плоскости Оху, с боков — цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 216). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z = f(x; у) на плоскость Оху) произвольным образом на п областей  , площади которых равны A
, площади которых равны A Рассмотрим цилиндрические столбики с основаниями ограниченные сверху кусками поверхности z = f(x;y) (на рис. 216 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием
Рассмотрим цилиндрические столбики с основаниями ограниченные сверху кусками поверхности z = f(x;y) (на рис. 216 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием  через
через  , получим
, получим
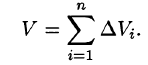
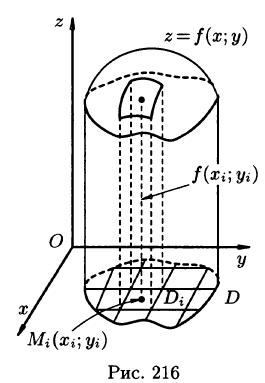
Возьмем на каждой площадке Di произвольную точку 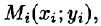 и заменим каждый столбик прямым цилиндром с тем же основанием
и заменим каждый столбик прямым цилиндром с тем же основанием  и высотой
и высотой 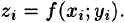 Объем этого цилиндра приближенно равен объему
Объем этого цилиндра приближенно равен объему 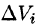 цилиндрического столбика, т. е.
цилиндрического столбика, т. е. 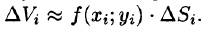 Тогда получаем:
Тогда получаем:
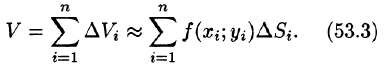
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей»  ,. Естественно принять предел суммы (53.3) при условии, что число площадок
,. Естественно принять предел суммы (53.3) при условии, что число площадок  неограниченно увеличивается
неограниченно увеличивается 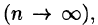 а каждая площадка стягивается в точку
а каждая площадка стягивается в точку 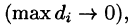 за объем V цилиндрического тела, т. е.
за объем V цилиндрического тела, т. е.
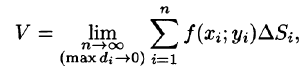
или, согласно равенству (53.2),
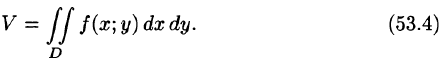
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу m плоской пластинки D. зная, что ее поверхностная плотность 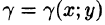 есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей
есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей 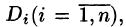 площади которых обозначим через
площади которых обозначим через 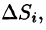 . В каждой области
. В каждой области  возьмем произвольную точку
возьмем произвольную точку 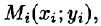 и вычислим плотность в ней:
и вычислим плотность в ней: 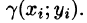
Если области D, достаточно малы, то плотность в каждой точке 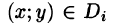 мало отличается от значения
мало отличается от значения 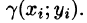 Считая приближенно плотность в каждой точке области
Считая приближенно плотность в каждой точке области  постоянной, равной
постоянной, равной 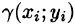 , можно найти ее массу
, можно найти ее массу 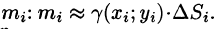 Так как масса m всей пластинки D равна
Так как масса m всей пластинки D равна 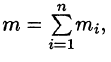 Для ее вычисления имеем приближенное равенство
Для ее вычисления имеем приближенное равенство
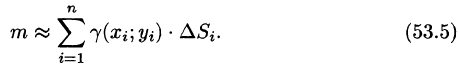
Точное значение массы получим как предел суммы (53.5) при условии 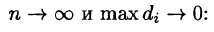
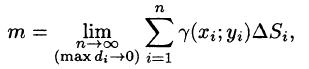
или, согласно равенству (53.2),
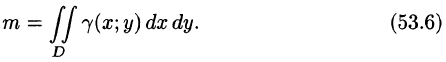
Итак, двойной интеграл от функции 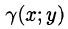 численно равен массе пластинки, если подынтегральную функцию
численно равен массе пластинки, если подынтегральную функцию 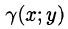 считать плотностью этой пластинки в точке (х; у). В этом состоит физический смысл двойного интеграла.
считать плотностью этой пластинки в точке (х; у). В этом состоит физический смысл двойного интеграла.
Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. § 35). Аналогичны и свойства этих интегралов и их доказательства (см. § 38). Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
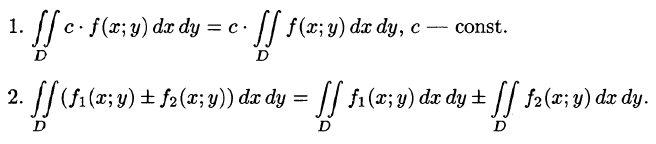
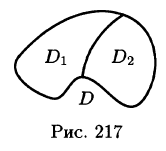
3.Если область D разбить линией на две области 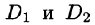 такие, что
такие, что 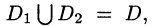 а пересечение
а пересечение 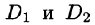 состоит лишь из линии, их разделяющей (см. рис. 217), то
состоит лишь из линии, их разделяющей (см. рис. 217), то
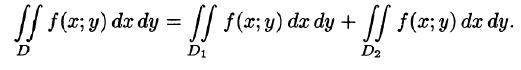
4.Если в области D имеет место неравенство 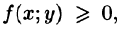 то и
то и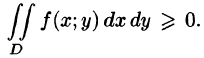 Если в области D функции f(x;y) и
Если в области D функции f(x;y) и 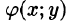 удовлетворяют неравенству
удовлетворяют неравенству 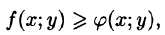 то и
то и
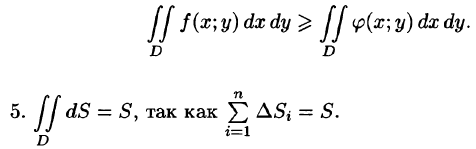
6.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой 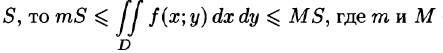 — соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
— соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
7.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка , что
, что 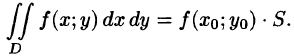 Величину
Величину
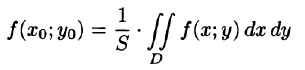
называют средним значением функции f(x; у) в области D.
Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 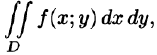 где функция
где функция 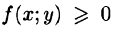 непрерывна в области D. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z = f(x;y). Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
непрерывна в области D. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z = f(x;y). Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
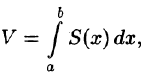
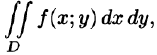
где S(x) — площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b — уравнения плоскостей, ограничивающих данное тело.
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b и кривыми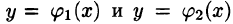 , причем функции
, причем функции 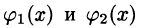 непрерывны и таковы, что
непрерывны и таковы, что 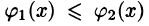 для всех
для всех 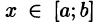 (см. рис. 218). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.
(см. рис. 218). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси 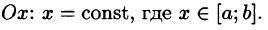
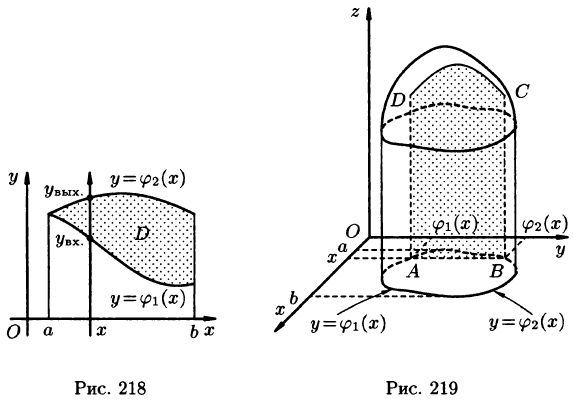
В сечении получим криволинейную трапецию ABCD, ограниченную линиями
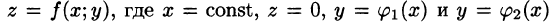
(см. рис. 219).
Площадь S(x) этой трапеции находим с помощью определенного интеграла
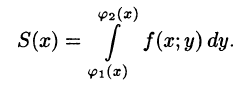
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
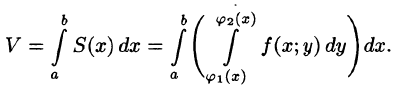
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 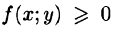 по области D. Следовательно,
по области D. Следовательно,
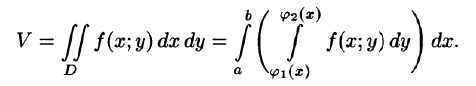
Это равенство обычно записывается в виде
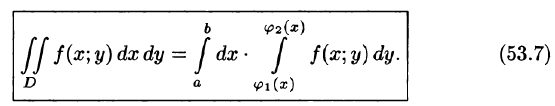
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции f(x;y) по области D. При этом 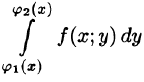 называется внутренним интегралом.
называется внутренним интегралом.
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
Если же область D ограничена прямыми  кривыми
кривыми
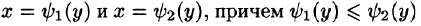
для всех 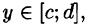 т. е. область D — правильная в направлении оси Ох, то, рассекая тело плоскостью у = const, аналогично получим:
т. е. область D — правильная в направлении оси Ох, то, рассекая тело плоскостью у = const, аналогично получим:
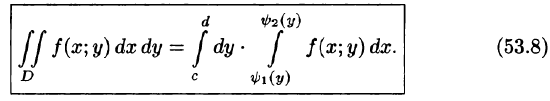
Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Замечания:
- Формулы (53.7) и (53.8) справедливы и в случае, когда
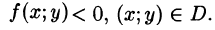
- Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
- Если область D не является правильной ни «по x», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ох или оси Оу.
- Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример:
Вычислить 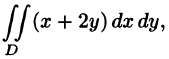 где область D ограничена линиями у
где область D ограничена линиями у
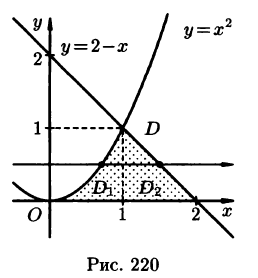
Решение:
На рисунке 220 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
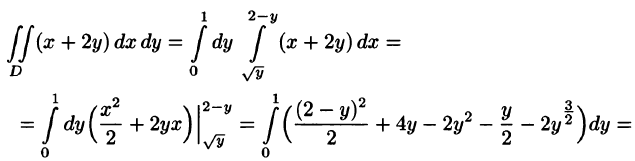
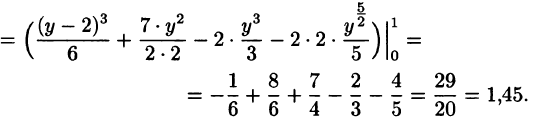
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область D следует разбить на две области:  . Получаем:
. Получаем:
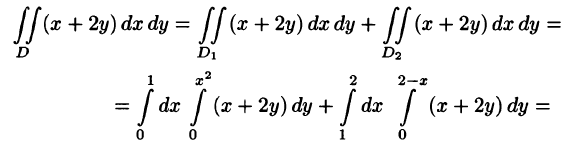
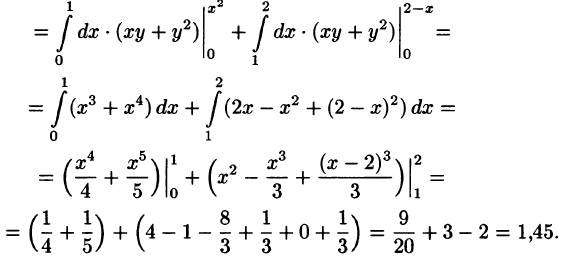
Ответ, разумеется, один и тот же.
Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
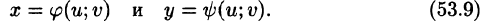
Если функции (53.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель

а функция f(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
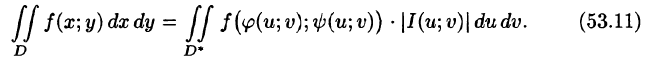
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами 
В качестве инь возьмем полярные координаты  Они связаны с декартовыми координатами формулами
Они связаны с декартовыми координатами формулами 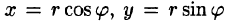 (см. п. 9.1).
(см. п. 9.1).
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
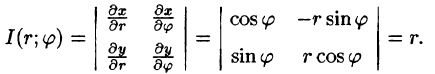
Формула замены переменных (53.11) принимает вид:
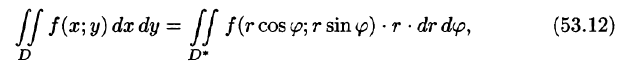
где D* — область в полярной системе координат, соответствующая области D в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами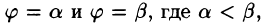 и кривыми
и кривыми 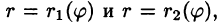 где
где 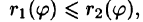 т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
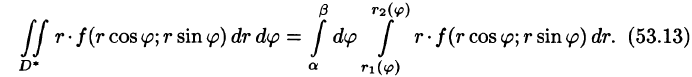
Внутренний интеграл берется при постоянном 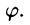
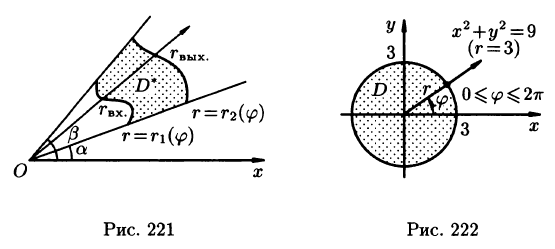
Замечания:
- Переход к полярным координатам полезен, когда подынтегральная функция имеет вид
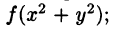 область D есть круг, кольцо или часть таковых.
область D есть круг, кольцо или часть таковых. - На практике переход к полярным координатам осуществляется путем замены
 уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по  (исследуя закон изменения
(исследуя закон изменения 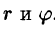 точки
точки 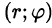 при ее отождествлении с точкой (х; у) области D).
при ее отождествлении с точкой (х; у) области D).
Пример:
Вычислить 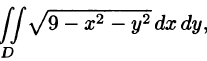 где область D — круг
где область D — круг 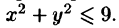
Решение: Применив формулу (53.12), перейдем к полярным координатам:
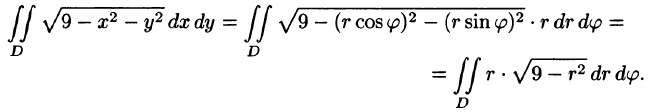
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 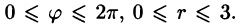 Заметим: область D —круг — преобразуется в область D* — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
Заметим: область D —круг — преобразуется в область D* — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
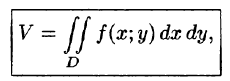
где z = f(x;y) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
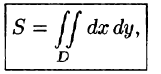
или, в полярных координатах,
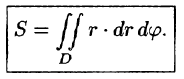
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 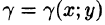 находится по формуле
находится по формуле
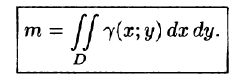
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
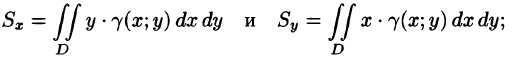
а координаты центра масс фигуры по формулам
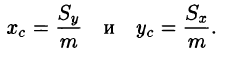
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. 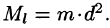 Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
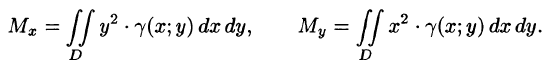
Момент инерции фигуры относительно начала координат — по формуле 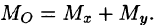
Замечание:
Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример:
Найти объем тела, ограниченного поверхностями
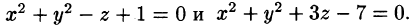
Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
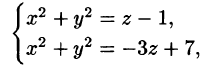
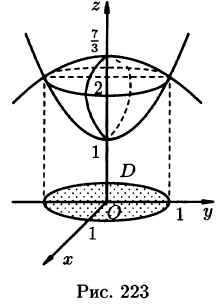
находим уравнение линии их пересечения:
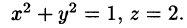
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 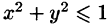 ) и ограниченных сверху соответственно поверхностями
) и ограниченных сверху соответственно поверхностями 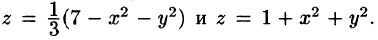 Используя формулу (53.4), имеем
Используя формулу (53.4), имеем
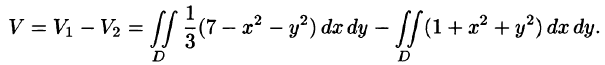
Переходя к полярным координатам, находим:
Пример:
Найти массу, статические моменты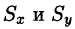 и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом
и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом 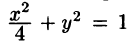 и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
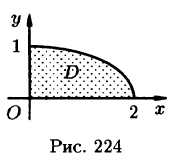
Решение: По формуле (53.6) находим массу пластинки. По условию, 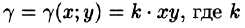 — коэффициент пропорциональности.
— коэффициент пропорциональности.
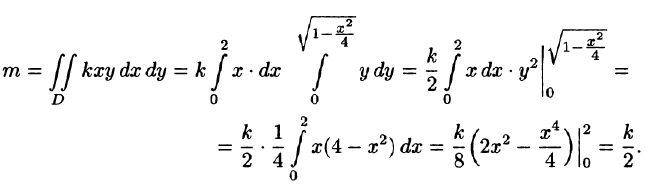
Находим статические моменты пластинки:
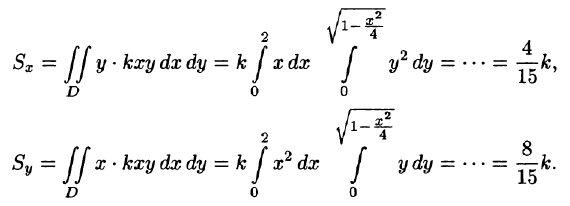
Находим координаты центра тяжести пластинки, используя формулы
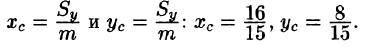
Двойной интеграл












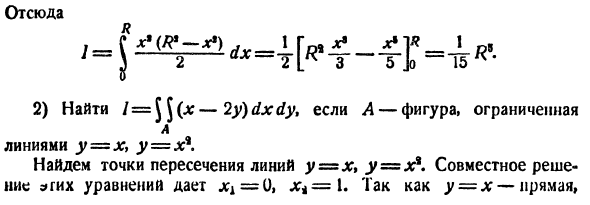

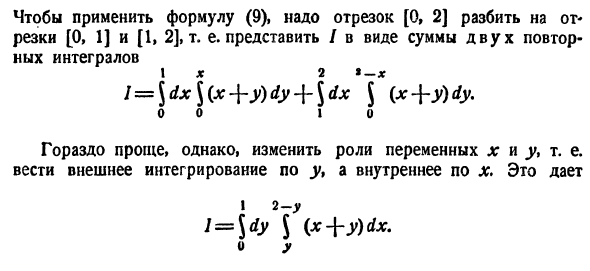

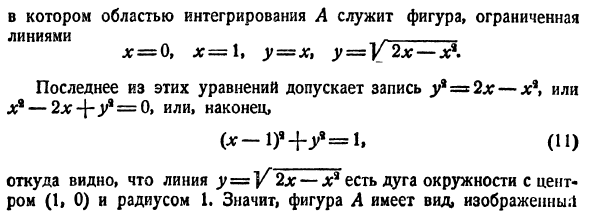














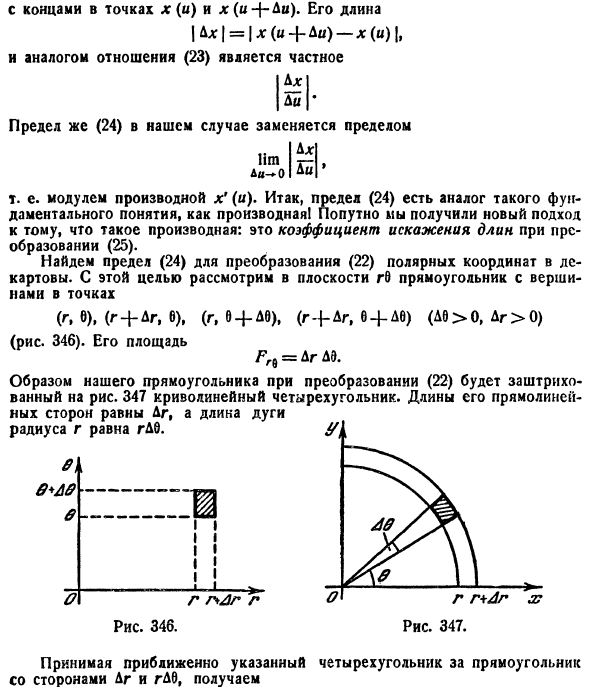


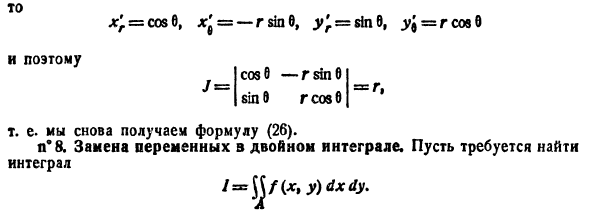

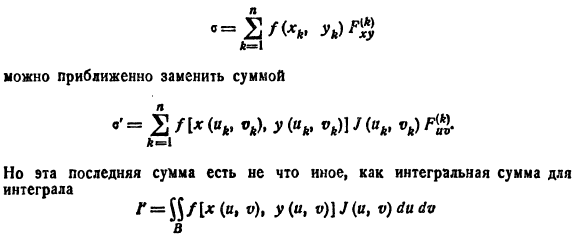




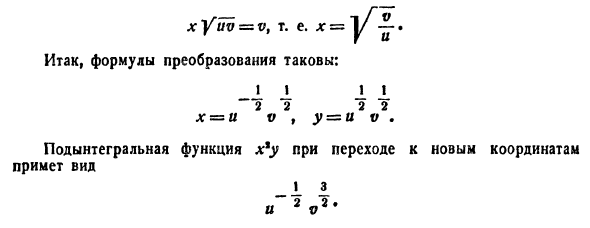





Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

