Mensuration is the part of mathematics that deals with studying various geometrical shapes, their areas, and volume. In simple terms, mensuration is all about measurement. The measurement of various body dimensions and calculation of area, surface area, and volume are studied under mensuration.
Volume
Volume is defined as a 3-dimensional space that is closed or bound by an object. Finding the volume of an object can help us to determine the quantity needed to fill an object, such as the water needed to fill a bottle, a swimming pool, or a water tank. The volume of an object is estimated in cubic units such as cubic centimeters, cubic inch, cubic foot, cubic meter, etc.
The volume of most objects can be easily calculated given the base area and height, even complex ones. The complex objects can be segmented into simpler figures, and thus adding the volumes of these simpler figures can be summed to obtain the volume of the entire object.
How to find the volume using the area and height?
In order to find the volume of a given object, it can be done in the following ways,
- Find the base area
- Multiply the base area with the corresponding height.
Calculating the volume of some familiar figures,
Cube
A cube is a three-dimensional object that has six congruent square faces. Dimensions of all the 6 square faces of the cube are identical. A cube is seldom also ascribed to as a regular hexahedron or as a square prism.
The base area of a cube = side × side
Height of the cube = side
Volume of the cube = base area × height = side3
Cuboid
A cuboid is a three-dimensional solid shape that has six faces, eight vertices, and 12 edges. It is one of the common shapes around us, which has three dimensions: length, width, and height.
The base area of the cuboid = Length × Breadth
Height of the cuboid = Depth
Volume of the cuboid = base area × height = Length × Breadth × Depth
Cylinder
A cylinder is a three-dimensional solid figure in geometry, which has two parallel circular bases bounded by a curved surface at a precise distance from the center. Candles, batteries are real-life examples of cylinders.
The base area of a cylinder = 3.14 × R2
Height of the cylinder = Length
Volume of the cylinder = base area x height = 3.14 × R2 × Length
Sample Problems
Question 1: The base area of a cube is 25 cm2, and the height is 5 cm. Find the volume.
Solution:
Volume = base area × height
= 25 × 5
= 125 cm3
Question 2: The base area of a cuboid is 10 cm2, and the height is 50 cm. Find the volume.
Solution:
Volume = base area × height
= 10 x 50
= 500 cm3
Question 3: The base area of a cylinder is 30 cm2, and its length is 10 cm. Find its volume.
Solution:
Volume = base area × height
= 30 × 10
= 300 cm2
Last Updated :
28 Sep, 2021
Like Article
Save Article
Как найти объем, если известны длина, высота, ширина
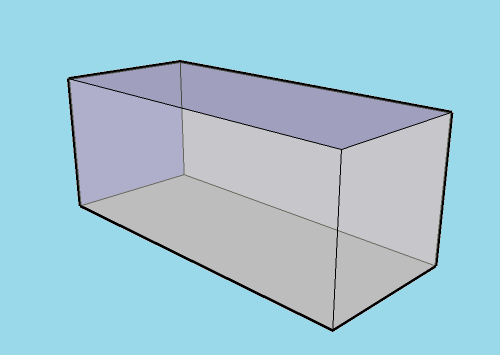
Длина, ширина, высота – это параметры, которые характеризуют параллелепипед. Сам же параллелепипед представляет собой объемную фигуру, грани которой – параллелограммы. Достаточно знать эти параметры, чтобы вычислить объем фигуры.
Вам понадобится
- Калькулятор.
Инструкция
Предварительно нужно сделать оговорку. Длина, ширина и высота – это параметры, которые являются достаточными для вычисления объема лишь у прямоугольного параллелепипеда. Под прямоугольным параллелепипедом подразумевается фигура, у которой все грани образованы прямоугольниками, которые образуют между собой прямые углы. Это означает, что в прямоугольном параллелепипеде противоположные грани равны и параллельны.
Теперь, разобравшись с тем, в каком случае можно применять в качестве исходных данных параметры параллелепипеда, можно приступить к вычислению его объема. Объем – это мера, характеризующая количество занимаемого объектом пространства. Для вычисления объема параллелепипеда необходимо перемножить друг на друга все его параметры: длину, ширину и высоту. Формулой это можно выразить так:
V = a*b*c, где a, b и с – это параметры.
Для большей наглядности можно рассмотреть пример:
Имеется прямоугольный параллелепипед, площадь основания которого равна 42 см², а его высота составляет 15 см, требуется найти объем исходной фигуры.
Для решения задачи нужно заметить, что из всех параметров известной является только высота. Но дана площадь основания, которая находится умножением друг на друга длины и ширины прямоугольника. Из указанной выше формулы можно сделать вывод, что площадь основания – это a*b см², тогда объем прямоугольного параллелепипеда найдется так:
42*15 = 630 см³
Ответ: объем фигуры составит 630 см³
Обратите внимание
В широкой интерпретации, параллелепипед – это призма, у которой в основании находится параллелограмм. Существует несколько разновидностей данной фигуры, среди которых, помимо прямоугольного параллелепипеда, имеются:
– Прямой параллелепипед, у которого боковые грани являются прямоугольниками;
– Наклонный параллелепипед, в котором боковые грани не являются перпендикулярными основанию;
– Куб – это особая разновидность данного типа фигур, ведь все грани у него являются квадратами. При пересечении они образуют прямые углы, а противоположные грани параллельны друг другу, а это означает, что куб – частный случай прямоугольного параллелепипеда
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
|
Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический! Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии. автор вопроса выбрал этот ответ лучшим
Ксарфакс 5 лет назад Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной. Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой. Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м. Самый простейший пример – объём помещения Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда. V = abc. a – длина, b – ширина, c – высота. Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой. Если вы знаете площадь, то посчитать объём ещё проще – достаточно измерить высоту и умножить это значение на данное значение. Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м. V = 6 * 5 * 2,5 = 75 м³.
Nelli4ka 5 лет назад Для примера возьмем прямоугольник и параллелепипед. Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных. Параллелепипед – фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула.
Galina7v7 7 лет назад Если ваш вопрос трактовать так: “как посчитать объём 1 метра кубического , то V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ. Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота. ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах.
Zolotynka 5 лет назад В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота. ** Данная формула имеет важное практическое значение. Рассмотрим на примере: Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона – 100 мм. Формула для расчета объема бетона в м3 будет выглядеть следующими образом: 2,0 × 2,0 × 0,1 = 0.4m3
Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно – длину умножить на ширину и умножить на высоту. Kerbal Space Program 6 лет назад Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра. Например, имеем: Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см. Эти длины переведем в метры и получим:
Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических.
moreljuba 5 лет назад Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических. FantomeRU 5 лет назад Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать.
vksvovko 6 лет назад Один из распространенных способов найти объем предмета неправильной формы – это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3.
EvgeniyAlekseevich 7 лет назад Высоту, выраженную в м3, умножить на длину и умножить на ширину. Знаете ответ? |
RAF
Профи
(688)
16 лет назад
Перемножить
gineotis_r_s@mail.ru
Ученик
(129)
16 лет назад
Вычитать друг из друга пока не получится НУЛЬ
Анна .
Гуру
(3086)
16 лет назад
Перемножить высоту,длину и ширину.
анима
Гуру
(4223)
16 лет назад
всё перемножить надо…вроде…
ШУМОК
Гуру
(4042)
16 лет назад
Вычислить объем бруска, зная его длину – 50 см, ширину – 2 дм, высоту – 4 м
http://www.home-edu.ru/user/f/00001501/Vveden/tema_f1.html
Дмитрий Блохин
Мудрец
(15377)
16 лет назад
а у бутылки диаметр вместо ширины,так что ничем помочь не могу.
Кузнецов Алексей
Ученик
(205)
16 лет назад
измерить литровыми банками с водой(наливаешь и считаешь)
Ольга Никитина
Профи
(505)
16 лет назад
смотря объем чего )) если фигура – прямоугольный параллелипипед, то перемножаешь все данные и все. с другими фигурами посложнее
Dulsineya
Гуру
(4171)
16 лет назад
Перемножить, нафик)))) )
Ток, пред этим привести к общему знаменателю, например к см.)))
Алексей Гонтаренко
Мастер
(1851)
16 лет назад
Если я ничего не забыл, сначала надо умножить длину на ширину, потом высоту на произведение длины и ширины. Только в таком порядке, а то все испортится
Uliana_2003
Мыслитель
(7677)
16 лет назад
Это все знают: V=a*b*c
Мария
Гуру
(2866)
16 лет назад
вес перемножить!!!!
окс
Профи
(627)
16 лет назад
Этот вопрос очень сложный и ты никогда не найдешь на него ответ
в учебнике для для 3-го класса
Пользователь удален
Знаток
(302)
16 лет назад
V=abc
а-ширина
b-длинна
с-высота
V-объём
Антон
Гуру
(3802)
16 лет назад
John ай молодца!!
Трололо Трололо
Ученик
(184)
6 лет назад
Ладно, скажем, что размеры бруска равны: 5 см*4 см*20 см=400 см^3 – объём.
Источник: Рада была помочь!
Асия
Ученик
(247)
4 года назад
найти длину, зная ширину 50 см, высоту 100 см и кубатуру 1,236 м2 ???

a – сторона куба
Формула объема куба, (V):


a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
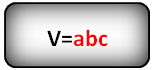

R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):

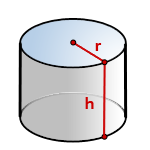
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

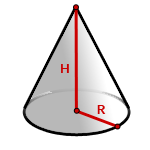
R – радиус основания
H – высота конуса
π ≈ 3.14
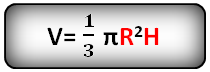
Формула объема конуса, если известны радиус и высота (V):
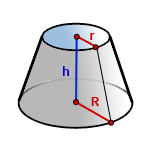
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

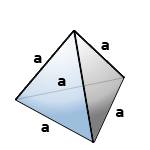
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
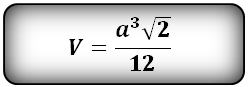
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
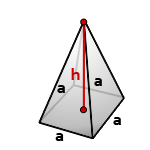
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
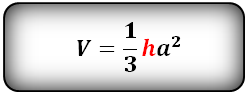
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
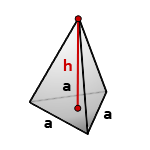
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
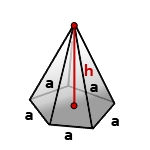
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
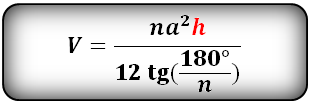
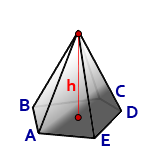
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
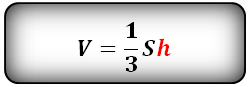
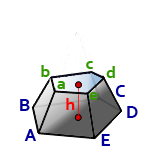
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
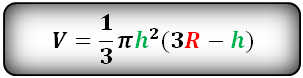
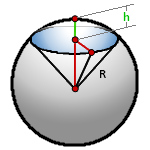
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):

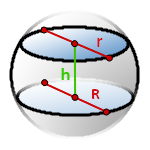
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):