Как найти объем сегмента сферы

Как найти объем сегмента сферы

У этого термина существуют и другие значения, см. сегмент.

Пример сферического сегмента (окрашен синим цветом). Вторая половина сферы также представляет собой сферический сегмент

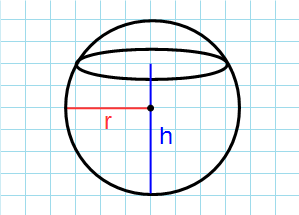
Сфери́ческий сегме́нт — поверхность, часть сферы, отсекаемая от неё некоторой плоскостью. Плоскость отсекает два сегмента: меньший сегмент называется также сферическим кругом[1].
Если секущая плоскость проходит через центр сферы, то высота обоих сегментов равна радиусу сферы, и каждый из таких сферических сегментов называют полусферой.

Шарово́й сегме́нт — геометрическое тело, часть шара, отсекаемая от него некоторой плоскостью. Поверхностью шарового сегмента является объединение сферического сегмента и круга (основания шарового сегмента), границы которых совпадают.

Объём и площадь поверхности[править | править код]

Если радиус основания сегмента равен a, высота сегмента равна h, тогда объём шарового сегмента равен [2]

{displaystyle V={frac {pi h}{6}}(3a^{2}+h^{2}),}

площадь поверхности сегмента равна

{displaystyle A=2pi rh}

или

{displaystyle A=2pi r^{2}(1-cos theta ).}

Параметры a, h и r связаны соотношениями

{displaystyle r^{2}=(r-h)^{2}+a^{2}=r^{2}+h^{2}-2rh+a^{2},}
{displaystyle r={frac {a^{2}+h^{2}}{2h}}.}

Подстановка последнего выражения в первую формулу для вычисления площади приводит к равенству

{displaystyle A=2pi {frac {(a^{2}+h^{2})}{2h}}h=pi (a^{2}+h^{2}).}

Заметим, что в верхней части сферы (синий сегмент на рисунке) {displaystyle h=r-{sqrt {r^{2}-a^{2}}},} в нижней части сферы {displaystyle h=r+{sqrt {r^{2}-a^{2}}},} следовательно, для обоих сегментов справедливо выражение {displaystyle a={sqrt {h(2r-h)}}} и можно привести другое выражение для объёма:

{displaystyle V={frac {pi h^{2}}{3}}(3r-h).}

Формула для определения объёма также может быть получена при интегрировании поверхности вращения:

{displaystyle V=int _{x}^{r}pi left(r^{2}-x^{2}right)dx=pi left({frac {2}{3}}r^{3}-r^{2}x+{frac {1}{3}}x^{3}right)={frac {pi }{3}}r^{3}(cos theta +2)(cos theta -1)^{2}.}

Применение[править | править код]

Объём объединения и пересечения двух пересекающихся сфер[править | править код]

Объём объединения двух сфер радиусов r1 и r2 равен
[3]

{displaystyle V=V^{(1)}-V^{(2)}},

где

{displaystyle V^{(1)}={frac {4pi }{3}}r_{1}^{3}+{frac {4pi }{3}}r_{2}^{3}}

является суммой объёмов двух сфер по отдельности, а

{displaystyle V^{(2)}={frac {pi h_{1}^{2}}{3}}(3r_{1}-h_{1})+{frac {pi h_{2}^{2}}{3}}(3r_{2}-h_{2})}

является суммой объёмов двух сферических сегментов, образующих пересечение данных сфер. Пусть d < r1 + r2 — расстояние между центрами сфер, тогда исключение величин h1 и h2 приводит к выражению [4][5]

{displaystyle V^{(2)}={frac {pi }{12d}}(r_{1}+r_{2}-d)^{2}left(d^{2}+2d(r_{1}+r_{2})-3(r_{1}-r_{2})^{2}right).}

Площадь поверхности, ограниченной кругами разных широт[править | править код]

Площадь поверхности, ограниченной кругами разных широт, является разностью площадей поверхности двух соответствующих сферических сегментов. Для сферы радиуса r и широт φ1 и φ2 данная площадь равна [6]

{displaystyle A=2pi r^{2}|sin varphi _{1}-sin varphi _{2}|.}

Площадь квадратного участка поверхности шара[править | править код]

Участок, вырезанный на сфере радиуса r четырьмя дугами больших кругов, имеющими одинаковую угловую длину θ и попарно перпендикулярными (сферический квадрат, аналог квадрата на плоскости), имеет площадь

{displaystyle A=8r^{2}(1-cos theta /2).}

Если угол θ мал (по сравнению с 1 радианом), то справедливо приближённое равенство, основывающееся на приближении {displaystyle cos xto 1-x^{2}/2} при {displaystyle xto 0:}

{displaystyle Aapprox 8r^{2}{frac {theta ^{2}}{8}}=r^{2}theta ^{2}.}

Например, площадь квадратного участка поверхности Земли (R⊕ = 6378 км) со сторонами, равными 1 градусу, составляет

{displaystyle A(1^{circ })=8cdot R_{oplus }^{2}(1-cos 0{,}5^{circ })approx R_{oplus }^{2}cdot left({frac {pi }{180}}right)^{2}approx 12,391,{text{км}}^{2}.}

1 квадратная секунда поверхности Земли имеет площадь в 36002 раз меньше: A(1′′) ≈ 12 391 км2 / (60 · 60)2 ≈ 956 м2.

Обобщения[править | править код]

Сечения других тел[править | править код]

Сфероидальный сегмент получается при отсечении части сфероида таким образом, что она обладает круговой симметрией (обладает осью вращения). Аналогичным образом определяют эллипсоидальный сегмент.

Сегмент гиперсферы[править | править код]

Объём n-мерного сегмента гиперсферы высотой h и радиуса r в n-мерном евклидовом пространстве определяется по формуле [7]

{displaystyle V={frac {pi ^{frac {n-1}{2}},r^{n}}{,Gamma left({frac {n+1}{2}}right)}}int limits _{0}^{arccos left({frac {r-h}{r}}right)}sin ^{n}t,mathrm {d} t,}

где Gamma (гамма-функция) задаётся выражением {displaystyle Gamma (z)=int _{0}^{infty }t^{z-1}mathrm {e} ^{-t},mathrm {d} t.}

Выражение для объёма V можно переписать в терминах объёма единичного n-мерного шара {displaystyle C_{n}={pi ^{n/2}/Gamma left[1+{frac {n}{2}}right]}} и гипергеометрической функции {displaystyle {}_{2}F_{1}} или регуляризованной неполной бета-функции {displaystyle I_{x}(a,b)} как

{displaystyle V=C_{n},r^{n}left({frac {1}{2}},-,{frac {r-h}{r}},{frac {Gamma [1+{frac {n}{2}}]}{{sqrt {pi }},Gamma [{frac {n+1}{2}}]}}{,,}_{2}F_{1}left({tfrac {1}{2}},{tfrac {1-n}{2}};{tfrac {3}{2}};left({tfrac {r-h}{r}}right)^{2}right)right)={frac {1}{2}}C_{n},r^{n}I_{(2rh-h^{2})/r^{2}}left({frac {n+1}{2}},{frac {1}{2}}right).}

Формула для площади поверхности A может быть записана в терминах площади поверхности единичного n-мерного шара {displaystyle A_{n}={2pi ^{n/2}/Gamma left[{frac {n}{2}}right]}} как

{displaystyle A={frac {1}{2}}A_{n},r^{n-1}I_{(2rh-h^{2})/r^{2}}left({frac {n-1}{2}},{frac {1}{2}}right),}

где {displaystyle 0leq hleq r.}

Также справедливы следующие формулы[8]:
{displaystyle A=A_{n}p_{n-2}(q),quad V=V_{n}p_{n}(q),} где
{displaystyle q=1-h/r(0leq qleq 1),quad p_{n}(q)={frac {1-G_{n}(q)/G_{n}(1)}{2}},}

{displaystyle G_{n}(q)=int limits _{0}^{q}(1-t^{2})^{(n-1)/2}dt.}

При {displaystyle n=2k+1:}

{displaystyle G_{n}(q)=sum _{i=0}^{k}(-1)^{i}{binom {k}{i}}{frac {q^{2i+1}}{2i+1}}.}

Было показано[9], что при {displaystyle nto infty } и {displaystyle q{sqrt {n}}={text{const }}} {displaystyle p_{n}(q)to 1-F({q{sqrt {n}}}),} где {displaystyle F()} — стандартное нормальное распределение.

Литература[править | править код]

  • А. И. Маркушевич, А. Я. Хинчин, П. С. Александров. Основные понятия сферической геометрии // Энциклопедия элементарной математики. Книга 4 – Геометрия. — Москва: ГИФМЛ, 1963.

Примечания[править | править код]

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем сегмента шара, а также разберем пример решения задачи для закрепления теоретического материала.

  • Определение сегмента шара

  • Формулы для нахождения объема шарового сегмента

    • Через радиус шара и высоту сегмента

    • Через радиус основания сегмента и его высоту

  • Пример задачи

Определение сегмента шара

Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.

Сегмент шара

  • R – радиус шара;
  • r – радиус основания сегмента;
  • h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.

Формулы для нахождения объема шарового сегмента

Пояснения:

  • В формулах ниже используется радиус шара (R) или радиус основания сегмента (r). Поэтому, если изначально дан их диаметр (d), то чтобы найти требуемый радиус, нужно соответствующий диаметр разделить на два.
  • Число π округленно равняется до 3,14.

Через радиус шара и высоту сегмента

Чтобы найти объем (V) сегмента шара, необходимо знать радиус шара и высоту сегмента.

Формула для нахождения объема сегмента шара через его высоту и радиус шара

Через радиус основания сегмента и его высоту

Вычислить объем (V) шарового сегмента можно, зная его высоту и радиус основания (круга).

Формула для нахождения объема сегмента шара через радиус его основания и высоту

Данная формула получена следующим образом:

Радиус шара можно выразить через радиус основания сегмента и его высоту:

Связь между радиусом основания сегмента, его высотой и радиусом шара:

Таким образом, заменив R в первой формуле для расчета объема на выражение выше, получаем:

Получение формулы для нахождения объема сегмента шара через радиус его основания и высоту

Пример задачи

Найдите объем сегмента шара, если известно, что его высота равняется 4 см, а радиус шара – 9 см.

Решение

В данном случае с учетом известных значений нам подходит первая формула:

Пример нахождения объема сегмента шара

Источник

Как рассчитать объем шарового сегмента

На данной странице калькулятор поможет рассчитать объем шарового сегмента онлайн. Для расчета задайте радиус и высоту. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.

Шаровой сегмент — часть шара, отсекаемая от него какой-нибудь плоскостью.

Через радиус и высоту

Объем шарового сегмента

Формула объема шарового сегмента через радиус и высоту:

π – константа равная (3.14); r – радиус шара; h – высота шарового сегмента.

Источник
Понятие шарового сегмента

Если пересечь шар какой-либо плоскостью, то он разделиться на две части, каждая из которых и будет представлять собой шаровой сегмент. Иногда его также называют сферическим сегментом.

Онлайн-калькулятор объема шарового сегмента

Меньший из этих сегментов принято называть сферическим кругом. Если же центр сферы лежит на плоскости, пересекающей шар, то он делится на два равных полушара.

Формула объема шарового сегмента

Объем данного тела можно вычислить несколькими способами. Первая формула такова:

1. Объем шарового сегмента

V=13⋅π⋅h2⋅(3⋅R−h)V=frac{1}{3}cdotpicdot h^2cdot(3cdot R-h)

hh —высота шарового сегмента;
RR — радиус шара.

Альтернативная формула:

2. Объем шарового сегмента

V=16⋅π⋅h⋅(3⋅r2+h2)V=frac{1}{6}cdotpicdot hcdot(3cdot r^2+h^2)

hh —высота шарового сегмента;
rr — радиус основания шарового сегмента.

Вторую формулу можно получить из первой, если использовать связь между RR, hh и rr:

R=r2+h22⋅hR=frac{r^2+h^2}{2cdot h},

получаемую с помощью теоремы Пифагора для прямоугольного треугольника.

Ниже приведены примеры задач на нахождение объемов шарового сегмента.

Задача 1

Вычислите объем шарового сегмента, если известны его высота и радиус основания. Равны они, соответственно, 4 см4text{ см} и 8 см8text{ см}.

Решение

h=4h=4
r=8r=8

По второй формуле получаем:

V=16⋅π⋅h⋅(3⋅r2+h2)=16⋅π⋅4⋅(3⋅82+42)≈435.4 см3V=frac{1}{6}cdotpicdot hcdot(3cdot r^2+h^2)=frac{1}{6}cdotpicdot 4cdot(3cdot 8^2+4^2)approx435.4text{ см}^3

Ответ

435.4 см3.435.4text{ см}^3.

Задача 2

Рассмотрим предыдущую задачу, но проделаем вычисления по другой формуле. Для этого нам нужно найти радиус шара RR.

Решение

h=4h=4
r=8r=8

R=r2+h22⋅h=82+422⋅4=10R=frac{r^2+h^2}{2cdot h}=frac{8^2+4^2}{2cdot 4}=10

Объем сегмента:

V=13⋅π⋅h2⋅(3⋅R−h)=13⋅π⋅42⋅(3⋅10−4)≈435.4 см3V=frac{1}{3}cdotpicdot h^2cdot(3cdot R-h)=frac{1}{3}cdotpicdot 4^2cdot(3cdot 10-4)approx435.4text{ см}^3

Исходя из полученных ответов можно сделать вывод, что данная формула справедлива, так как ответы полученные разными формулами совпадают.

Ответ

435.4 см3.435.4text{ см}^3.

Задача 3

Определить объем шарового сегмента, если площадь его поверхности равна 64 см64text{ см}, а высота – 5см5text {см}.

Решение

S=64S=64
h=5h=5

Для начала найдем радиус RR шара. Площадь поверхности шарового сегмента можно найти так:

S=2⋅π⋅R⋅hS=2cdotpicdot Rcdot h.

Найдем отсюда радиус RR шара:

R=S2⋅π⋅h=642⋅π⋅5≈2R=frac{S}{2cdotpicdot h}=frac{64}{2cdotpicdot 5}approx2

Объем шарового сегмента по формуле:

V=13⋅π⋅h2⋅(3⋅R−h)≈13⋅π⋅52⋅(3⋅2−5)≈26 см3V=frac{1}{3}cdotpicdot h^2cdot(3cdot R-h)approxfrac{1}{3}cdotpicdot 5^2cdot(3cdot 2-5)approx26text{ см}^3

Ответ

26 см3.26text{ см}^3.

Хотите заказать выполнение контрольной работы у опытного исполнителя? Оформите заказ на нашей бирже!

Источник

Объем шарового сегмента, формула

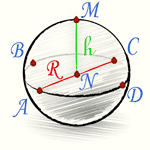
Объем шарового сегмента
Часть шара, [шар, сфера] осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется круг ABCD. Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра, восстановленного из центра N основания до пересечения с поверхностью шара. Точка M называется вершиной шарового сегмента.

Объем шарового сегмента выражается формулой:

[ V = pi h^2 ( R – frac{1}{3} h ) ]

(R – радиус большого круга шара, h – высота шарового сегмента)

Формулы шара, сферы

Вычислить, найти объем шарового сегмента по формуле (1)

Объем шарового сегмента

 стр. 344
Источник

Добавить комментарий