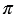Объём части конуса. Для вас очередная статья с конусами – тип заданий, которые ранее присутствовали в открытом банке задач и вполне могут быть в составе ЕГЭ по математике. *На момент написания статьи эти задания из открытого банка удалены, но их всегда могут вернуть вновь.
Суть вопроса заключается в нахождении объёма части конуса. На блоге уже есть статья с заданиями, условия которых связаны с объёмом конуса, можете посмотреть.
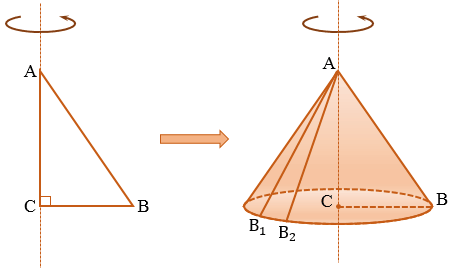
Если сказать простым языком – рассматриваемое тело построено («стоит») на секторе круга, то есть нам необходимо найти объём некоторого «сектора конуса». Посмотрите для наглядности, это рисунки из задач:
Как вы догадались – процесс решения прост!
Главное определить центральный угол сектора круга, на котором построена («стоит») часть конуса.
Формула объёма конуса:
Пока рассмотрим общий подход к решению. Посмотрите на эскизы, мысленно представьте, что это вид конуса сверху:
Мы знаем, что полный круг составляет у нас 3600.
Если «отрежем» часть конуса соответствующую центральному углу в 1800 (то есть, пополам по оси), то объём части конуса будет равен половине объёма полного конуса (рис.1):
Если мы «вырежем» часть конуса, соответствующую центральному углу в 900, то объём этой части будет равен одной четвёртой объёма полного конуса (рис.2):
При этом объём оставшейся части будет равен ¾ от объёма полного конуса:
Если мы «вырежем» часть конуса, соответствующую центральному углу в 600, то объём этой части будет равен одной шестой объёма полного конуса (рис.4):
То есть необходимо величину центрального угла, которая соответствует части конуса разделить на 3600, и далее полученную величину умножаем на полный объём конуса. Общая формула:
Рассмотрим задачи:
25793. Найдите объем V части конуса, изображённой на рисунке. В ответе укажите V/Пи.
Объём конуса равен:
Объем части конуса равен:
n – центральный угол, которому соответствует часть конуса
Таким образом, искомый объём равен:
Результат разделим на Пи и запишем ответ.
Ответ: 216
27203. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/Пи.
Угол соответствующий указанной части конуса равен 3600 – 900 = 2700.
Таким образом, искомый объём будет равен:
Результат разделим на Пи и запишем ответ.
Ответ: 243
27204. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/Пи.
Угол соответствующий указанной части конуса равен 600.
Таким образом, искомый объём будет равен:
Результат разделим на Пи и запишем ответ.
Ответ: 216
27205. Найдите объем V части конуса, изображенной на рисунке. В ответе укажите V/Пи.
Угол соответствующий указанной части конуса равен 3600 – 600 = 3000.
Таким образом, искомый объём будет равен:
Результат разделим на Пи и запишем ответ.
Ответ: 607,5
27202. Найдите объем части конуса, изображенной на рисунке.
В ответе укажите V/Пи.
Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
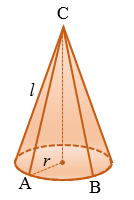
Площадь поверхности конуса состоит из площади боковой поверхности конуса и площади основания (круга).
|
Рис. (1). Конус |
Площадь боковой поверхности конуса вычисляется по формуле: где (R) — радиус конуса, (l) — образующая конуса. Площадь основания конуса вычисляется по формуле S(круга) = Площадь полной поверхности конуса вычисляется по формуле S(полн.) =S(бок.) +S(круга) =πRl+πR2. Объём конуса вычисляют по формуле V = 13⋅H⋅ S(круга) = πR2⋅H3 |
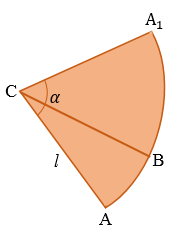
Площадью боковой поверхности конуса является площадь её развёртки.
Развёрткой боковой поверхности конуса является круговой сектор.
|
Рис. (2). Развёртка конуса |
α
— градусная мера центрального угла. Радиус этого сектора — образующая конуса (AK = KB = l)
|
Источники:
Рис. 1. Конус. © Якласс
Рис. 2. Развёртка конуса. © Якласс
Напомним,
что конус – это тело, полученное при вращении прямоугольного
треугольника вокруг прямой, проходящей через один из его катетов.
Назовём
элементы конуса.
Осью
конуса называется прямая вращения.
Основание конуса
– круг радиуса ,
который равен катету треугольника вращения.
Радиус
конуса –
это радиус его основания.
Вершина
конуса – неподвижная вершина треугольника вращения.
Образующая
конуса –
отрезок, соединяющий вершину конуса с любой точкой окружности основания. Все
образующие конуса равны между собой.
Высота конуса
–
перпендикуляр, опущенный из вершины конуса на плоскость его основания. Высота
конуса совпадает с неподвижным катетом треугольника вращения.
В
конусе радиус основания ,
высота и
образующая связаны
следующим соотношением:
.
Сечение
конуса плоскостью, проходящей через его вершину, представляет собой
равнобедренный треугольник, у которого боковые стороны являются образующими
конуса.
Осевым
сечением конуса называется сечение конуса плоскостью,
проходящей через его ось.
Осевое
сечение конуса – равнобедренный треугольник, боковые стороны
которого – образующие, а основание – диаметр основания конуса.
Боковую
поверхность конуса, как и боковую поверхность цилиндра,
можно развернуть на плоскость, разрезав её по одной из образующих. Развёрткой
боковой поверхности конуса является круговой сектор.
Обратите
внимание, радиус сектора равен образующей конуса,
а длина дуги сектора равна длине окружности основания конуса.
Площадь
боковой поверхности конуса можно вычислить по следующим
формулам:
,
,
,
где
–
длина окружности основания, –
радиус основания, –
образующая.
Площадь
полной поверхности конуса равна сумме площади боковой поверхности конуса и
площади его основания.
Тогда
площадь полной поверхности конуса можно вычислить по формуле^
,
где
–
радиус основания конуса, –
его образующая.
Объём конуса
равен одной третьей произведения площади основания на высоту.
Тогда
его можно вычислить по формуле:
,
где
–
радиус основания конуса, –
его высота.
Плоскость,
параллельная плоскости основания конуса, пересекает конус по кругу, а боковую
поверхность – по окружности с центром на оси конуса. Эта плоскость разбивает
конус на две части. Одна из частей (верхняя) представляет собой конус, а вторая
(нижняя) называется усечённым конусом.
Усечённым
конусом называется часть конуса, ограниченная его основанием
и сечением, параллельным плоскости основания. Усечённый конус имеет ось,
высоту ,
радиусы оснований и
,
образующую .
Осевое сечение усечённого конуса – равнобедренная трапеция.
Площадь
боковой поверхности усечённого конуса и объём усечённого конуса равен разности
площадей боковых поверхностей и объёмов полного конуса и отсечённого.
,
Площадь
боковой поверхности усечённого конуса можно найти по следующим
формулам:
,
Объём
усечённого конуса можно вычислить по следующим формулам:
,
где
и
–
площади оснований, –
высота усечённого конуса;
или
,
где
–
высота усечённого конуса, и
–
радиусы верхнего и нижнего оснований.
Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.
Задача
первая. Радиус основания конуса равен см,
высота конуса равна см.
Найдите площадь боковой поверхности и объём конуса.
Решение.
Задача
вторая. В конус вписана правильная треугольная пирамида с
площадью основания см2
и углом наклона бокового ребра к основанию, равным .
Найдите объём и площадь полной поверхности конуса.
Решение.
Задача
третья. В равносторонний конус с радиусом основания, равным см,
вписан прямоугольный параллелепипед в основании которого лежит квадрат, с
высотой см
так, что одно его основание принадлежит основанию конуса, а вершины другого
основания принадлежат боковой поверхности конуса. Найдите объём
параллелепипеда. В ответе запишите значение .
Решение.
Задача
четвёртая. Длины радиусов оснований и образующей усечённого
конуса равны соответственно см,
см
и см.
Вычислите его высоту.
Решение.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Многогранники
- Конус
Конус – это объемное тело, которое получается при вращении прямоугольного треугольника вокруг одного из его катетов.
Возьмем прямоугольный треугольник АВС. Будем вращать этот треугольник вокруг катета АС.
Прямая АС – ось косинуса.
Отрезок АС – высота конуса.
Основание конуса – круг, образованный при вращении катета ВС.
Коническая поверхность (или боковая поверхность конуса) – поверхность, образованная при вращении гипотенузы АВ и состоящая из отрезков с общим концом А.
Образующие конуса – отрезки, из которых составлена боковая поверхность конуса (на рисунке выше указаны образующие АВ, АВ1 и АВ2).
Определение
Конус – это тело, ограниченное кругом и конической поверхностью.
Объем конуса
Объем конуса равен одной трети произведения площади основания на высоту.
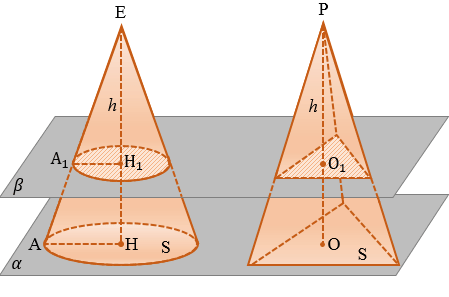
Доказательство
Дано: конус с площадью основания S, высотой h и объемом V.
Доказать: V =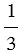 
Sh.
Доказательство:
Воспользуемся принципом Кавальери. Рассмотрим конус и пирамиду с площадями оснований S и высотами ЕН = h и РО = h соответственно, “стоящие” на одной плоскости 
.
Проведем секущую плоскость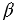 
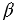
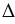
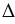
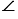
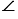
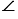
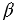
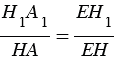
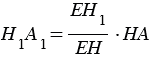
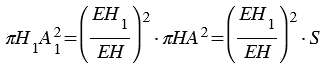
, параллельную плоскости и пересекающую высоты ЕН и РО в точках Н1 и О1 соответственно. В сечении конуса плоскостью получится круг радиуса Н1А1.
ЕН1А1 подобен ЕНА по двум углам (
Е – общий, ЕН1А1 = ЕНА = 900, т.к. в противном случае прямые НА и Н1А1, а значит, и плоскости и пересекались бы, что противоречит условию). Поэтому 
, откуда 
и площадь сечения конуса равна 
.
Площадь сечения пирамиды равна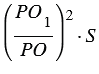 
. По условию ЕН = РО = h, значит, ЕН1 = РО1 (т.к. ЕН1 = h – НН1 и РО1 = h – ОО1, параллельные плоскости отсекают одинаковые отрезки НН1 и ОО1 от отрезков ЕН и РО, т.е. НН1 = ОО1).
Следовательно, площадь сечения конуса равна площади сечения пирамиды. Поэтому и его объем равен объему пирамиды, т.е. V = 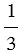Sh. Что и требовалось доказать.
Площадь боковой поверхности конуса
Рассмотрим конус с радиусом основания 
и образующей 
.
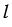
Представим, что его боковую поверхность разрезали по одной из образующих и развернули так, что получился круговой сектор.
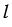
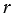
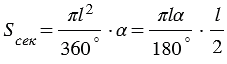
Радиус этого сектора равен образующей конуса, т.е. равен , а длина дуги сектора равна длине окружности основания конуса, т.е. равна 2
, – градусная мера дуги сектора, тогда площадь данного сектора: 
. (1)
Длина дуги окружности с градусной мерой и радиусом равна 
. С другой стороны, длина этой дуги равна 2, поэтому учитывая (1), получим: 
.
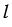
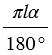
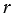
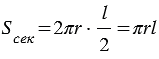
Площадь боковой поверхности конуса равна площади ее развертки, т.е.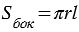 
.
Советуем посмотреть:
Предмет стереометрии
Параллельность и перпендикулярность прямых и плоскостей в пространстве
Многогранник
Призма
Параллелепипед
Объём тела
Свойства прямоугольного параллелепипеда
Пирамида
Цилиндр
Сфера и шар
Многогранники
Правило встречается в следующих упражнениях:
7 класс
Задание 1220,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1223,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1228,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 19,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 22,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1248,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1250,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1251,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1310,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
В данной публикации мы рассмотрим, каким образом можно посчитать объем прямого кругового конуса и разберем примеры решения задач.
-
Формула вычисления объема
- 1. Через площадь основания и высоту
- 2. Через радиус основания и высоту
- Примеры задач
Формула вычисления объема
1. Через площадь основания и высоту
Объем (V) конуса равняется одной третьей произведения его высоты на площадь основания:
2. Через радиус основания и высоту
Как мы знаем, основанием конуса является круг, площадь которого вычисляется по формуле: S = πR2.
Следовательно, формулу для вычисления объема конуса можно представить в виде:
Т.е. объем конуса равняется одной третьей произведения его высоты на число π и на радиус основания в квадрате.
Примечание: в расчетах значение числа π округляется до 3,14.
Формула для нахождения объема усеченного конуса представлена в отдельной публикации.
Примеры задач
Задание 1
Найдите объем конуса, если известна площадь его основания – 50,24 см2, а также, высота – 9 см.
Решение:
Применим первую формулу, подставив в нее заданные значения:
Задание 2
Высота конуса равна 7 см, а его радиус – 3 см. Найдите объем фигуры.
Решение:
Воспользовавшись второй, более расширенной, формулой получаем:
