Шаровой сектор – это часть шара, ограниченная кривой поверхностью шарового сегмента и конической
поверхностью, основанием которой служит основание сегмента, а вершиной центр шара. Другое
определение исходит из того, что шаровой сектор – тело вращения, т.е. образовано вращением
какой-либо плоской и ограниченной кривой геометрической фигуры вокруг лежащей в той же плоскости
оси. Объем шарового сегмента определяется рядом его размеров, ниже 2 формулы для вычисления
объема.
- Обьём шарового сектора через радиус шара и высоту шарового
сегмента - Обьём шарового сектора через радиус шара и угол между осью
и образующей конуса
Объём шарового сектора через радиус шара и высоту шарового сегмента
Зная радиус и высоту шарового сектора, можно найти его объем по следующей формуле:
V = 2/3 * π * R² * h
где R – радиус шара, h – высота шарового сегмента (или проекция хорды, стягивающей дугу сектора, на
ось вращения).
Цифр после
запятой:
Результат в:
Значение π примерно равно 3,14 – это числовая постоянная «число пи», одна из самых известных и чаще
всего использующихся, равная отношению длины окружности к ее диаметру; для всех окружностей это
отношение постоянно. «Пи» число иррациональное и трансцендентное, т.е. не может быть выражено
никакой рациональной дробью и не может быть корнем какого-либо многочлена с целыми
коэффициентами.
Пример. Радиус R = 5 м; h = 1,5 м. Рассчитываем объем: V = 2 * π * R² * h / 3 = 2 * 3,14 * 5² * 1,5 / 3 = 78,5 м³.
Объём шарового сектора через радиус шара и угол между осью и образующей конуса
При известном радиусе шара и угла между осью и образующей конуса можно так же найти объем шарового
сектора. Для это применяется формула:
V = 2/3 * π * R³ * (1 — cos α/2)
где R – радиус шара, cos α – угол между осью и образующей конуса.
Цифр после
запятой:
Результат в:
Пример. Вафельный рожок для мороженого, при заполнении мороженым имеющий форму
шарового сектора, имеет такие размеры: радиус R = 11 см, угол α = 26°. Необходимо рассчитать объем
мороженого в рожке при его заполнении. V = 2/3 * 3,14 * 11³ * (1 — cos 26º/2) = 71 см³.
Шаровой сектор – это геометрическое тело, возникающее при вращении сектора вокруг одного из его
радиусов. Форму, близкую к шаровому сектору, имеют, в качестве примера, современные воздушные шары и
мороженое в вафельном рожке.
Как рассчитать объем шарового сектора
На данной странице калькулятор поможет рассчитать объем шарового сектора онлайн. Для расчета задайте радиус и высоту. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара.
Через радиус и высоту
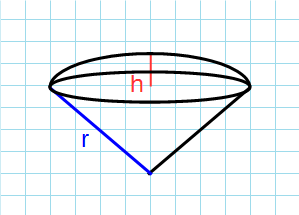
Формула объема шарового сектора через радиус и высоту:
π – константа равная (3.14); r – радиус шара; h – высота шарового сегмента.
В данной публикации мы рассмотрим формулу, с помощью которой можно вычислить объем сектора шара, а также пример решения задачи для демонстрации ее применения на практике.
- Определение сектора шара
- Формула для нахождения объема сектора шара
- Пример задачи
Определение сектора шара
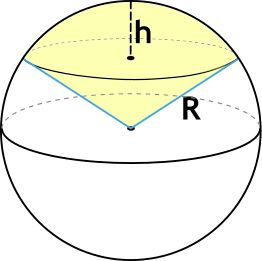
Сектор шара (или шаровый сектор) – это часть шара, состоящая из шарового сегмента и конуса, вершиной которого является центр шара, а основанием – основание соответствующего сегмента. На рисунке ниже сектор закрашен оранжевым цветом.

- R – радиус шара;
- r – радиус основания сегмента и конуса;
- h – высота сегмента; перпендикуляр от центра основания сегмента до точки на сфере.
Формула для нахождения объема сектора шара
Чтобы найти объем шарового сектора, необходимо знать радиус шара и высоту соответствующего сегмента.
![]()
Примечания:
- если вместо радиуса шара (R) дан его диаметр (d), последний следует разделить на два, чтобы найти требуемый радиус.
- π округленно равняется 3,14.
Пример задачи
Дан шар радиусом 12 см. Найдите объем шарового сектора, если высота сегмента, из которого состоит данный сектор, равняется 3 см.
Решение
Применим формулу, рассмотренную выше, подставив в нее известные по условиям задачи значения:
![]()
Если пересечь шар какой-либо плоскостью, то он разделиться на две части, каждая из которых и будет представлять собой шаровой сегмент. Иногда его также называют сферическим сегментом.
Онлайн-калькулятор объема шарового сегмента
Меньший из этих сегментов принято называть сферическим кругом. Если же центр сферы лежит на плоскости, пересекающей шар, то он делится на два равных полушара.
Формула объема шарового сегмента
Объем данного тела можно вычислить несколькими способами. Первая формула такова:
V=13⋅π⋅h2⋅(3⋅R−h)V=frac{1}{3}cdotpicdot h^2cdot(3cdot R-h)
hh —высота шарового сегмента;
RR — радиус шара.
Альтернативная формула:
V=16⋅π⋅h⋅(3⋅r2+h2)V=frac{1}{6}cdotpicdot hcdot(3cdot r^2+h^2)
hh —высота шарового сегмента;
rr — радиус основания шарового сегмента.
Вторую формулу можно получить из первой, если использовать связь между RR, hh и rr:
R=r2+h22⋅hR=frac{r^2+h^2}{2cdot h},
получаемую с помощью теоремы Пифагора для прямоугольного треугольника.
Ниже приведены примеры задач на нахождение объемов шарового сегмента.
Вычислите объем шарового сегмента, если известны его высота и радиус основания. Равны они, соответственно, 4 см4text{ см} и 8 см8text{ см}.
Решение
h=4h=4
r=8r=8
По второй формуле получаем:
V=16⋅π⋅h⋅(3⋅r2+h2)=16⋅π⋅4⋅(3⋅82+42)≈435.4 см3V=frac{1}{6}cdotpicdot hcdot(3cdot r^2+h^2)=frac{1}{6}cdotpicdot 4cdot(3cdot 8^2+4^2)approx435.4text{ см}^3
Ответ
435.4 см3.435.4text{ см}^3.
Рассмотрим предыдущую задачу, но проделаем вычисления по другой формуле. Для этого нам нужно найти радиус шара RR.
Решение
h=4h=4
r=8r=8
R=r2+h22⋅h=82+422⋅4=10R=frac{r^2+h^2}{2cdot h}=frac{8^2+4^2}{2cdot 4}=10
Объем сегмента:
V=13⋅π⋅h2⋅(3⋅R−h)=13⋅π⋅42⋅(3⋅10−4)≈435.4 см3V=frac{1}{3}cdotpicdot h^2cdot(3cdot R-h)=frac{1}{3}cdotpicdot 4^2cdot(3cdot 10-4)approx435.4text{ см}^3
Исходя из полученных ответов можно сделать вывод, что данная формула справедлива, так как ответы полученные разными формулами совпадают.
Ответ
435.4 см3.435.4text{ см}^3.
Определить объем шарового сегмента, если площадь его поверхности равна 64 см64text{ см}, а высота – 5см5text {см}.
Решение
S=64S=64
h=5h=5
Для начала найдем радиус RR шара. Площадь поверхности шарового сегмента можно найти так:
S=2⋅π⋅R⋅hS=2cdotpicdot Rcdot h.
Найдем отсюда радиус RR шара:
R=S2⋅π⋅h=642⋅π⋅5≈2R=frac{S}{2cdotpicdot h}=frac{64}{2cdotpicdot 5}approx2
Объем шарового сегмента по формуле:
V=13⋅π⋅h2⋅(3⋅R−h)≈13⋅π⋅52⋅(3⋅2−5)≈26 см3V=frac{1}{3}cdotpicdot h^2cdot(3cdot R-h)approxfrac{1}{3}cdotpicdot 5^2cdot(3cdot 2-5)approx26text{ см}^3
Ответ
26 см3.26text{ см}^3.
Хотите заказать выполнение контрольной работы у опытного исполнителя? Оформите заказ на нашей бирже!
На странице вы сможете рассчитать объем шарового сектора. Для этого мы подготовили калькулятор и формулу для расчета объема шарового сектора. Просто введите радиус шара и высоту сегмента и тут же получите результат.
Шаровый сектор – тело, получаемое вращением кругового сектора с углом, меньшим 90°, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Формула объёма шарового сектора
{V= dfrac{2}{3}pi R^2 h}
R – радиус шара
h – высота шарового сегмента
Примеры задач на нахождение объема шарового сегмента
Задача 1
Найдите объем шарового сегмента, если радиус шара равен 8 см, а высота сегмента – 3см.
Решение
Подставим значения в формулу и получим результат.
V = dfrac{2}{3}pi R^2 h = dfrac{2}{cancel{3}}pi cdot 8^2 cdot cancel{3} = 128 pi : см^3 approx 402.12386 : см^3
Ответ: 128 pi : см^3 approx 402.12386 : см^3
Проверить результат удобно с помощью калькулятора .
