В данной публикации мы рассмотрим формулу, с помощью которой можно вычислить объем сектора шара, а также пример решения задачи для демонстрации ее применения на практике.
- Определение сектора шара
- Формула для нахождения объема сектора шара
- Пример задачи
Определение сектора шара
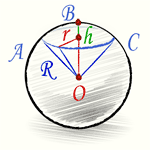
Сектор шара (или шаровый сектор) – это часть шара, состоящая из шарового сегмента и конуса, вершиной которого является центр шара, а основанием – основание соответствующего сегмента. На рисунке ниже сектор закрашен оранжевым цветом.
- R – радиус шара;
- r – радиус основания сегмента и конуса;
- h – высота сегмента; перпендикуляр от центра основания сегмента до точки на сфере.
Формула для нахождения объема сектора шара
Чтобы найти объем шарового сектора, необходимо знать радиус шара и высоту соответствующего сегмента.
Примечания:
- если вместо радиуса шара (R) дан его диаметр (d), последний следует разделить на два, чтобы найти требуемый радиус.
- π округленно равняется 3,14.
Пример задачи
Дан шар радиусом 12 см. Найдите объем шарового сектора, если высота сегмента, из которого состоит данный сектор, равняется 3 см.
Решение
Применим формулу, рассмотренную выше, подставив в нее известные по условиям задачи значения:
Шаровой сектор – это часть шара, ограниченная кривой поверхностью шарового сегмента и конической
поверхностью, основанием которой служит основание сегмента, а вершиной центр шара. Другое
определение исходит из того, что шаровой сектор – тело вращения, т.е. образовано вращением
какой-либо плоской и ограниченной кривой геометрической фигуры вокруг лежащей в той же плоскости
оси. Объем шарового сегмента определяется рядом его размеров, ниже 2 формулы для вычисления
объема.
- Обьём шарового сектора через радиус шара и высоту шарового
сегмента - Обьём шарового сектора через радиус шара и угол между осью
и образующей конуса
Объём шарового сектора через радиус шара и высоту шарового сегмента
Зная радиус и высоту шарового сектора, можно найти его объем по следующей формуле:
V = 2/3 * π * R² * h
где R – радиус шара, h – высота шарового сегмента (или проекция хорды, стягивающей дугу сектора, на
ось вращения).
Цифр после
запятой:
Результат в:
Значение π примерно равно 3,14 – это числовая постоянная «число пи», одна из самых известных и чаще
всего использующихся, равная отношению длины окружности к ее диаметру; для всех окружностей это
отношение постоянно. «Пи» число иррациональное и трансцендентное, т.е. не может быть выражено
никакой рациональной дробью и не может быть корнем какого-либо многочлена с целыми
коэффициентами.
Пример. Радиус R = 5 м; h = 1,5 м. Рассчитываем объем: V = 2 * π * R² * h / 3 = 2 * 3,14 * 5² * 1,5 / 3 = 78,5 м³.
Объём шарового сектора через радиус шара и угол между осью и образующей конуса
При известном радиусе шара и угла между осью и образующей конуса можно так же найти объем шарового
сектора. Для это применяется формула:
V = 2/3 * π * R³ * (1 — cos α/2)
где R – радиус шара, cos α – угол между осью и образующей конуса.
Цифр после
запятой:
Результат в:
Пример. Вафельный рожок для мороженого, при заполнении мороженым имеющий форму
шарового сектора, имеет такие размеры: радиус R = 11 см, угол α = 26°. Необходимо рассчитать объем
мороженого в рожке при его заполнении. V = 2/3 * 3,14 * 11³ * (1 — cos 26º/2) = 71 см³.
Шаровой сектор – это геометрическое тело, возникающее при вращении сектора вокруг одного из его
радиусов. Форму, близкую к шаровому сектору, имеют, в качестве примера, современные воздушные шары и
мороженое в вафельном рожке.
Шаровой сектор — это тело, которое можно получить при вращении сектора круга вокруг какого-либо из его радиусов, не пересекающего хорду этого кругового сектора.
Онлайн-калькулятор объема шарового сектора
Формула объема шарового сектора
Объем шарового сектора можно найти по такой формуле:
V=23⋅π⋅R2⋅hV=frac{2}{3}cdotpicdot R^2cdot h
RR —радиус шарового сектора;
hh — высота шарового сектора (проекция хорды, которая стягивает дугу кругового сектора на его ось вращения при получении таким образом шарового сектора).
Формула объема шарового сектора как объем пирамиды
Существует еще одна формула, с помощью которой можно найти искомый объем.
Она равна объему пирамиды, у которой площадь основания численно равна площади части сферической поверхности, которая вырезается сектором. Высота пирамиды равна радиусу шарового сектора.
V=13⋅R⋅SV=frac{1}{3}cdot Rcdot S
RR —радиус шарового сектора (высота соответствующей пирамиды);
SS — площадь основания пирамиды.
Разберем решение задач на данную тему.
Вычислите объем сектора шара, если его радиус равен 10 см10text{ см}, а высота – 7 см7text{ см}.
Решение
R=10R=10
h=7h=7
По первой формуле получаем:
V=23⋅π⋅R2⋅h=23⋅π⋅102⋅7≈1465 см3V=frac{2}{3}cdotpicdot R^2cdot h=frac{2}{3}cdotpicdot 10^2cdot 7approx1465text{ см}^3
Ответ
1465 см3.1465text{ см}^3.
Определить объем шарового сектора, если площадь основания соответствующей пирамиды равна 24 см224text{ см}^2, а ее высота равна 8 см8text{ см}.
Решение
S=24S=24
R=8R=8
Используем вторую формулу для объема шарового сектора:
V=13⋅R⋅S=13⋅8⋅24=64 см3V=frac{1}{3}cdot Rcdot S=frac{1}{3}cdot 8cdot 24=64text{ см}^3
Ответ
64 см3.64text{ см}^3.
Не знаете, где найти решение задач на заказ недорого? На нашем сайте есть профильные исполнители, которые помогут вам в этом!
Тест по теме “Объем шарового сектора”
Объем шарового сектора, формула
Шаровой сектор — это часть шара [шар, сфера], ограниченная кривой поверхностью шарового сегмента и конической поверхностью основанием которой служит основание сегмента, а вершиной — центр шара.
Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара:
[ V = frac{1}{3} R S = frac{2}{3} pi R^2 h ]
h — высота шарового сегмента, принадлежащего шаровому сектору.
Формулы шара, сферы
Вычислить, найти объем шарового сектора по формуле(1)
Объем шарового сектора |
стр. 346 |
|---|
Как рассчитать объем шарового сектора
На данной странице калькулятор поможет рассчитать объем шарового сектора онлайн. Для расчета задайте радиус и высоту. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара.
Через радиус и высоту
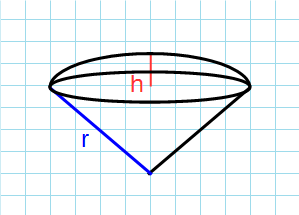
Формула объема шарового сектора через радиус и высоту:
π – константа равная (3.14); r – радиус шара; h – высота шарового сегмента.