Как найти объем сферы формула

Загрузить PDF

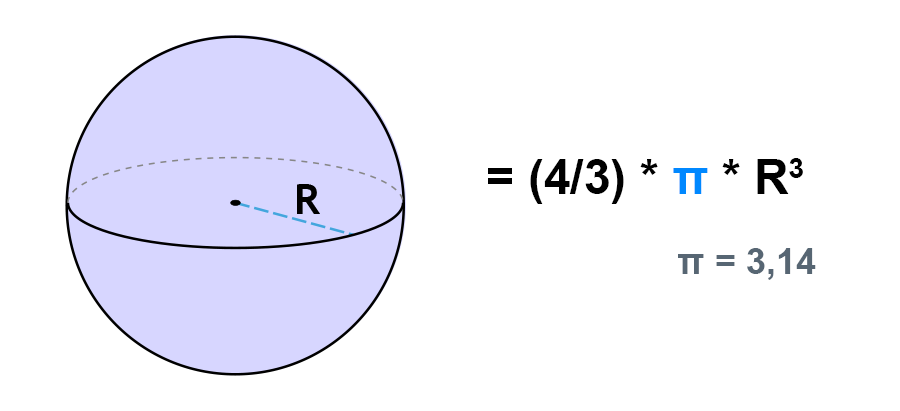
Сфера — это абсолютно круглая геометрическая фигура, у которой каждая точка поверхности равноудалена от центральной точки.^[1] Многие предметы, например шары или глобусы, являются сферами. Чтобы вычислить объем сферы, нужно найти ее радиус и воспользоваться простой формулой: V = ⁴/₃πr³.^[2]

1

Запишите формулу для вычисления объема сферы. Формула: V = ⁴/₃πr³, где V — объем, r — радиус сферы.
2
Найдите радиус. Если радиус дан, перейдите к следующему шагу. Если дан диаметр, разделите его на два, чтобы найти радиус.^[3] Когда вы вычислите радиус, запишите его. Например, радиус равен 3 см.^[4]
- Если дана только площадь поверхности сферы, вычислите радиус так: площадь поверхности разделите на 4π, а затем из полученного значения извлеките квадратный корень. Таким образом: r = √(S/4π), где S — площадь поверхности сферы.^[5]
3
Возведите радиус в куб. Для этого умножьте радиус на себя три раза или возведите его в третью степень. Например, 3³ = 3 * 3 * 3 = 27. Когда будете записывать окончательный ответ, не забудьте про единицу измерения (в нашем примере это кубические сантиметры). Теперь найденное значение подставьте в формулу для вычисления объема сферы (V = ⁴/₃πr³). Таким образом: V = ⁴/₃π * 27.
- Если радиус равен 5 см, то кубический радиус равен 5³ = 5 * 5 * 5 = 125.
4

Кубический радиус умножьте на 4/3. Вы подставили в формулу значение r³ (в нашем примере 27); теперь умножьте это значение на 4/3: 4/3 * 27 = 36. Теперь формула запишется так: V = ⁴/₃ * π * 27 = 36π.
5

Умножьте полученное значение на π. Это последний шаг процесса вычисления объема сферы. Можно оставить π и записать ответ так: V = 36π. Или вместо π подставьте численное значение этой константы (π ≈ 3,14)^[6]: V = 3,14 * 36 = 113,04 ≈ 113. Не забудьте указать кубические единицы измерения. Таким образом, объем шара с радиусом 3 см приблизительно равен 113 см³.

Реклама

Советы

Используйте кубические единицы измерения (например, 113 см³).
Убедитесь, что все значения представлены в одной единице измерения. В противном случае преобразуйте единицы измерения.
Обратите внимание, что символ «*» используется как знак умножения, чтобы избежать путаницы с переменной «x».
Если нужно найти объем некоторой части сферы, например, ее половины или четверти, сначала вычислите объем всей сферы, а затем полученное значение разделите на число, на которое поделена сфера. Например, чтобы найти объем полусферы, когда объем всей сферы равен 8, разделите 8 на 2 и получите 4.

Что вам понадобится

Калькулятор (чтобы не делать сложные вычисления в уме)
Карандаш и бумага (не нужны, если есть многофункциональный калькулятор)

Об этой статье

Эту страницу просматривали 37 438 раз.

Была ли эта статья полезной?

Источник

Калькулятор объема шара

Рассчитайте онлайн объем любой шарообразной фигуры по ее радиусу или диаметру.

Что известно

Длина

Размерность

Раcсчитать

Оглавление:

📝 Как это работает?
🤔 Частые вопросы и ответы
📋 Похожие материалы
📢 Поделиться и комментировать

Что такое калькулятор объема шара или сферы?

Калькулятор объема шара — это онлайн инструмент, который используется для быстрого расчета объема шара по его радиусу или диаметру. Объем шара представляет собой объем пространства, которое занимает шар в трехмерном пространстве.

Калькулятор объема шара может быть полезным инструментом для учебных заданий или практических задач, связанных с расчетами объемов шаров. Он также может использоваться в различных профессиональных областях, где необходимы точные расчеты объемов, например, в архитектуре, инженерии, физике и т.д.

🌎 Где можно применить калькулятор объема шара?

Калькулятор объема шара может быть полезным инструментом в различных областях и сферах деятельности, например:

Архитектура и строительство: при проектировании и строительстве куполов, бассейнов, шарообразных крыш и других шарообразных конструкций.
Медицина: при расчете объема опухолей, кровеносных сосудов, сердца и других органов.
Производство и промышленность: при расчете объема шарообразных резервуаров, емкостей, шарообразных деталей и т.д.
Космология: при расчете объема планет, галактик и других космических объектов.
Физика: при расчете объема и массы материалов, например, при изучении свойств и характеристик материалов.
Образование: при выполнении учебных заданий и проектов в школе, вузе и других образовательных учреждениях.
Различные хобби и увлечения: при создании шарообразных фигур, скульптур, шариков для игр и других творческих проектов.

Калькулятор объема шара может быть полезным инструментом во многих ситуациях, когда необходимо быстро и точно вычислить объем шара.

🔮 В чем преимущество шарообразной формы?

Шарообразная форма имеет несколько преимуществ, которые делают ее полезной в различных областях:

Минимальная поверхность: шарообразная форма имеет минимальную поверхность в отношении своего объема. Это значит, что на единицу объема шара приходится меньше поверхности, чем на единицу объема других форм, что может быть полезно, например, для сокращения издержек при производстве.
Равномерность нагрузки: шарообразная форма имеет равномерное распределение нагрузки на поверхности, что позволяет ей лучше выдерживать внешнее давление.
Сферическая симметрия: шарообразная форма имеет сферическую симметрию, что означает, что она выглядит одинаково при любом повороте вокруг своей оси. Это может быть полезным, например, при проектировании оптических систем, таких как линзы и зеркала.
Простота: шарообразная форма является одной из самых простых геометрических форм, и ее параметры (радиус, диаметр, объем и т.д.) легко вычисляются.
Эстетика: шарообразная форма считается эстетичной и привлекательной для взгляда. Она широко используется в дизайне, искусстве и архитектуре для создания красивых и уникальных форм.

Как вычислить объем шара через радиус?

Калькулятор объема шара обычно использует стандартную математическую формулу для расчета объема шара, которая основана на его радиусе. Формула для расчета объема шара выглядит следующим образом:

V = (4/3) * π * r³

где V – объем шара, r – радиус шара, pi – константа, примерно равная 3.14159.

Как вычислить объем шара через диаметр?

Чтобы вычислить объем шара через его диаметр, можно использовать следующую формулу:

V = (4/3) * π * (d/2)³

где V – объем шара, d – диаметр шара, π – число Пи, математическая константа, равная приблизительно 3,14159.

Для расчета объема шара нужно возвести значение d/2 в куб и умножить результат на 4/3 и на π.

❓ Вопросы и ответы

А вот несколько ответов на часто задаваемы вопросе о шаре и его объеме.

Как пользоваться онлайн калькулятором объема шара?

Для того, чтобы использовать калькулятор объема шара, нужно ввести значение радиуса шара или его диаметра в соответствующее поле калькулятора, затем калькулятор автоматически рассчитает объем шара.

Что такое шар?

Шар — это трехмерная геометрическая фигура, которая представляет собой идеальную сферу в трёхмерном пространстве. Все точки поверхности шара находятся на одинаковом расстоянии от его центра.

Для чего нужен расчет объема шара?

Расчет объема шара может быть полезен для решения различных задач в науке, технике и повседневной жизни. Например, зная объем шара, можно вычислить массу сферического объекта, если известна его плотность. Также расчет объема шара может использоваться при проектировании сферических емкостей или устройств.

Какой материал лучше всего подходит для изготовления шаров?

Для изготовления шаров часто используют различные материалы, в том числе металлы, стекло, пластмассу и резину. Выбор материала зависит от конкретной задачи и требований к изделию. Например, если необходима высокая прочность, то лучше выбрать металлический шар, а если необходимо обеспечить прозрачность, то следует выбрать стеклянный шар.

Как найти радиус шара, если известен его объем?

Радиус шара может быть найден по формуле: r = ³√(3V/4π), где r – радиус шара, V – объем шара, π – число пи (3.14159265…).

Как найти диаметр шара, если известен его радиус?

Диаметр шара равен удвоенному радиусу, то есть d = 2r, где d – диаметр шара, r – радиус шара.

What is Volume of Sphere?

The volume of a sphere is the amount of space it takes up within it. The sphere is a three-dimensional round solid shape in which all points on its surface are equally spaced from its centre. The fixed distance is known as the sphere’s radius, and the fixed point is known as the sphere’s centre. We will notice a change in form when the circle is turned. As a result of the rotation of the two-dimensional object known as a circle, the three-dimensional shape of a sphere is obtained.

The formula for the volume of a sphere is given by,

V = 4/3πr³

where,

r = radius of the sphere

π = 22/7

Volume of Sphere Formula with its Derivation

Using the integration approach, we can simply calculate the volume of a sphere.

Suppose the sphere’s volume is made up of a series of thin circular discs stacked one on top of the other, as drawn in the diagram above. Each thin disc has a radius of r and a thickness of dy that is y distance from the x-axis.

Let the volume of a disc be dV. The value of dV is given by,

dV = (πr²)dy

dV = π (R² – y²)dy

The total volume of the sphere will be the sum of volumes of all these small discs. The required value can be obtained by integrating the expression from limit -R to R.

So, the volume of sphere becomes,

V = $int_{y=-R}^{y=R} dV$

= $int_{y=-R}^{y=R}π(R^2 - y^2)dy$

= $pi|(R^2y - frac{y^3}{3})dy|_{y=-R}^{y=R}$

= $pi left[R^3-frac{R^3}{3}-(-R^3+frac{R^3}{3})right]$

= $pi left[2R^3-frac{2R^3}{3}right]$

= $frac{4}{3}pi R^3$

Thus, the formula for volume of sphere is derived.

How to Calculate Volume of Sphere?

Volume of sphere is the space occupied by a sphere. Its volume can be calculated using the formula V = 4/3πr³. Steps required to calculate the volume of a sphere are:

Mark the value of the radius of the sphere.
Find the cube of the radius.
Multiply the cube of the radius by (4/3)π
Add the unit to the final answer.

Example: Find the volume of a sphere with a radius of 7 cm.

Solution:

The formula for volume of a sphere, V = (4/3)πr³
Given, r = 7 cm
Volume of sphere, V = ((4/3) × π × 7³) cm³
V = 1436.8 cm³
Thus, the volume of sphere is 1436.8 cm³

Volume of Cone

Volume of Cube

Volume of Cylinder

Solved Examples on Volume of Sphere

Example 1. Find the volume of the sphere whose radius is 9 cm.

Solution:

We have, r = 9.

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (9) (9) (9)

= (4) (3.14) (3) (9) (9)

= 3052 cm³

Example 2. Find the volume of the sphere whose radius is 12 cm.

Solution:

We have, r = 12

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (12) (12) (12)

= (4) (3.14) (4) (12) (12)

= 7234.56 cm³

Example 3. Find the volume of the sphere whose radius is 6 cm.

Solution:

We have, r = 6.

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (6) (6) (6)

= (4) (3.14) (2) (6) (6)

= 904.32 cm³

Example 4. Find the volume of the sphere whose radius is 4 cm.

Solution:

We have, r = 4.

Volume of sphere = 4/3 πr3

= (4/3) (3.14) (4) (4) (4)

= (1.33) (3.14) (4) (4) (4)

= 267.27 cm³

Example 5. Find the volume of the sphere whose diameter is 10 cm.

Solution:

We have, 2r = 10

=> r = 10/2

=> r = 5

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (5) (5) (5)

= (1.33) (3.14) (5) (5) (5)

= 522.025 cm³

Example 6. Find the volume of the sphere whose diameter is 16 cm.

Solution:

We have, 2r = 16

=> r = 16/2

=> r = 8

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (8) (8) (8)

= (1.33) (3.14) (8) (8) (8)

= 2138.21 cm³

Example 7. Find the volume of the sphere whose diameter is 14 cm.

Solution:

We have, 2r = 14

=> r = 14/2

=> r = 7

Volume of sphere = 4/3 πr³

= (4/3) (3.14) (7) (7) (7)

= (1.33) (3.14) (7) (7) (7)

= 1432.43 cm³

FAQs on Volume of Sphere

Question 1: Write the formula for the total surface area of the sphere.

Answer:

Total surface area of any sphere is given by:

Area = 4πr²

where ‘r’ is the radius of the given sphere.

Questions 2: What is the formula for the Volume of the Sphere?

Answer:

The volume of a sphere is given by:

Volume = 4/3πr³

where ‘r’ is the radius of the given sphere.

Question 3: How do we find the volume of Hemi-Sphere?

Answer:

The volume of a hemi-sphere is given by:

Volume = 2/3πr³

where ‘r’ is the radius of the given sphere.

Question 4: If a sphere and a hemisphere have the same radii then what is the ratio of their volume?

Answer:

If a sphere and a hemisphere have the same radii then the ratio of their volume is given by

V₁: V₂ = (4/3πr³) : (2/3πr³)

= 2 : 1

Question 5: How do we measure the volume of Sphere?

Answer:

The Volume of the Sphere is measured in m³, cm³, litres, etc.

m³is the standard unit of measurement.

Last Updated :
10 Aug, 2022

Like Article

Save Article

Источник

Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас
слышал про эту знаменитую спортивную игру. Всем известно,
что в футбол играют мячом.

Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть
людей скажут, что форму шара, а часть, что формы сферы. Так кто же
из них прав? И в чем разница между сферой и шаром?

Важно!

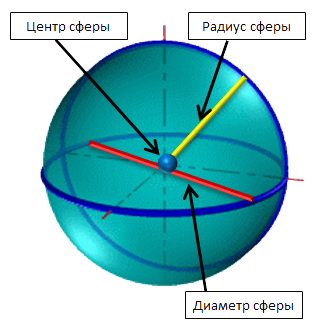
Шар — это пространственное тело. Внутри шар
чем-либо заполнен. Поэтому у шара можно найти объем.

Примеры шара в жизни: арбуз и стальной шарик.

Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.

Важно!

Сфера — поверхность шара. У сферы можно найти площадь поверхности.

Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.

Как найти площадь сферы

Запомните!

Формула площади сферы:
S = 4πR²

Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа.
Зная определение степени,
можно записать формулу площади сферы следующим образом.

S = 4π R² =
4πR · R;

Закрепим полученные знания и решим задачу на площадь сферы.

Зубарева 6 класс. Номер 692(а)

Условие задачи:

Вычислите площадь сферы, если её радиус равен
1 м. (возьмите π как
3)

Вспомнив, как выделить целую часть
и перемножить дроби,
воспользуемся формулой площади сферы:

S = 4 · πR² =
4 · 3 ·

(1 ) ² =

4 · ·

() ² =

4 · ·

= =

=
45
м²

Как найти объем шара

Запомните!

Формула объема шара:
V = πR³

Зная определение степени,
можно записать формулу объема шара следующим образом.

V =
π R³ =

π R · R · R;

Для отработки полученных знаний решим задачу на объем шара.

Зубарева 6 класс. Номер 691(а)

Условие задачи:

Вычислите радиус шара, если его объем равен
4 м³ (возьмите π как
3)

Выразим из формулы объема шара радиус.

V =
π R³
π R³
= V
π R³

=
R³

=

Подставим в формулу известные нам значения. Число π
возьмем как задано в задании «3».

R³

= (3 ·

4) /

(4 · 3)

Чтобы не запутаться, отдельно рассчитаем
числитель дроби.

3 ·
4 =

3 ·
=

Теперь снова подставим полученное значение в нашу формулу:

R³

=
/ (4 · 3)

=

/ (4 · )

=

/ () =

=

· () =

= =

=

= 1
R³ = 1
R = 1 м

Важно!

Уважаемые родители!

При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.

В 6 классе при решении такой задачи используйте метод перебора.

Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

14 февраля 2019 в 22:59

Руслан Магомедов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Руслан Магомедов
Профиль
Благодарили: 0

Сообщений: 1

Рассчитайте объем чашки высотой 7 см с диаметром 6,5 с

0
Спасибо thanks
Ответить

Источник

Советы

Что вам понадобится

Об этой статье

Была ли эта статья полезной?

Калькулятор объема шара

Что такое калькулятор объема шара или сферы?

🌎 Где можно применить калькулятор объема шара?

🔮 В чем преимущество шарообразной формы?

Как вычислить объем шара через радиус?

Как вычислить объем шара через диаметр?

❓ Вопросы и ответы