В данной публикации мы рассмотрим, как найти радиус описанной около конуса сферы, а также площадь ее поверхности и объем шара, ограниченного этой сферой.
- Нахождение радиуса сферы/шара
- Формулы площади и объема сферы/шара
Нахождение радиуса сферы/шара
Около любого конуса можно описать сферу (шар). Другими словами, в любую сферу можно вписать конус.

Чтобы найти радиус сферы (шара), описанной около конуса, чертим осевое сечение конуса. В итоге у нас получится равнобедренный треугольник (в нашем случае – ABC), вокруг которого описана окружность с радиусом r.

Радиус основания конуса (R) равен половине основания треугольника (AC), а образующие (l) – его боковые стороны (AB и BC).
Радиус окружности (r), описанной вокруг треугольника ABC, в том числе, является радиусом шара, описанного около конуса. Он находится по следующим формулам:
1. Через образующую и радиус основания конуса:

2. Через высоту и радиус основания конуса
![]()
Высота (h) конуса – это отрезок BE на рисунках выше.
Формулы площади и объема сферы/шара
Зная радиус (r) можно найти площадь поверхности (S) сферы и объем (V) шара, ограниченного этой сферой:
![]()

Примечание: π округленно равняется 3,14.
Задания
Версия для печати и копирования в MS Word
Тип 2 № 269539 
i
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 15. Найдите объем шара.
Решение.
Это задание ещё не решено, приводим решение прототипа.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Из формул для объема конуса и шара получаем:
Ответ: 24.
Аналоги к заданию № 245352: 269491 514181 269493 … Все
Классификатор стереометрии: Комбинации круглых тел, Объём цилиндра, конуса, шара
Прототип задания
·
Видеокурс
![]()
В данной статье рассмотрим четыре задачи по стереометрии. Дана комбинация тел – конус и шар. Во всех заданиях речь идёт о конусе, который вписан в шар. Отмечу, что в условии взаимное расположение данных тел озвучено может быть по разному, например: «Конус вписан в шар» или «Около конуса описана сфера».
Суть одна – если сказать простым (нематематическим) языком, то конус находится «внутри» сферы, она содержит окружность его основания и вершину. Посмотрите на эскиз:

При решении необходимо знать формулы объёмов шара и конуса.
Объём шара:

Объём конуса:

*Эти формулы необходимо знать!
Площадь основания конуса является кругом, она равна:

Рассмотрим частный случай! Если высота конуса будет равна радиусу его основания, то формула объёма конуса будет иметь вид:

Эскиз:

Понятно, что центральным сечением такого конуса будет являться прямоугольный равнобедренный треугольник, причём высота проведённая из прямого угла разбивает его также на два прямоугольных равнобедренных треугольника:

Вспомним понятие образующей, оно часто используется в задачах с конусами, будет и в заданиях ниже.
Образующая конуса – это отрезок, соединяющий вершину конуса с точкой его основания. На предыдущем эскизе она обозначена буквой l.
Напрашивается простой вывод: образующих у конуса имеется бесконечное количество и все они равны.
На блоге, кстати, уже есть пара статей с шарами, можете посмотреть их «Задачи с шарами. Это просто!» и «Цилиндр описан около шара. Три задачи».
Теперь рассмотрим задачи:

245351. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Так как сказано, что радиус основания конуса равен радиусу шара, то становится понятно, что основание конуса совпадает с плоскостью центрального сечения шара.
Построим эскиз данной комбинации для наглядности (это осевое сечение):

Сказано, что высота конуса равна радиусу его основания (и, разумеется, радиусу шара). Запишем формулы объёмов шара и конуса:

Так как объём шара известен (он равен 28), можем вычислить радиус. Вернее, нам понадобится не сам радиус, а его куб:

Таким образом, объём конуса будет равен:

*Можно было обойтись без вычислений. Посмотрите, если сопоставить две формулы:

то видно, что объём шара в 4 раза больше объёма конуса.
Значит объём конуса будет равен 28/4 = 7.
То есть, задача решается практически устно.
Ответ: 7

245352. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Задача обратная предыдущей, рисунок тот же.
Формулы:

Из формул понятно, что объём шара в 4 раза больше объёма конуса:

Таким образом, искомый объём равен 24.
Ответ: 24

316555. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна  . Найдите радиус сферы.
. Найдите радиус сферы.
Здесь условие звучит по-другому, но тела расположены относительно друг друга абсолютно также, как и в предыдущих задачах – конус вписан в сферу, основание конуса совпадает с центральным сечением сферы.
Эскиз тот же, отметим радиус, высоту равную радиусу и образующую:

Задача сводится к использованию одной формулы. Рассмотрим прямоугольный треугольник (выделен жёлтым). По теореме Пифагора:

Радиус сферы равен семи.
Ответ: 7

316556. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен  . Найдите образующую конуса.
. Найдите образующую конуса.
Эта задача обратная предыдущей, эскиз:

Рассмотрим прямоугольный треугольник (выделен жёлтым), х – это образующая. По теореме Пифагора:

Образующая конуса равна 56.
Ответ: 56
На этом всё. Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Подобные задачи чаще даются с радиусом конуса, равным радиусу шара.
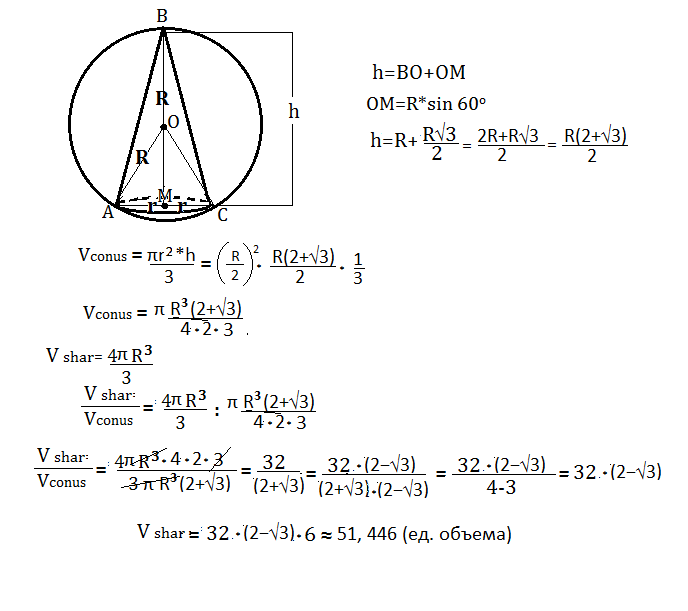
Т.к. диаметр основания конуса равен радиусу шара, радиус основания конуса равен половине радиуса шара, т.е. R/2
Высота конуса равна радиусу шара плюс высота правильного треугольника со сторонами, равными радиусу шара ( см. рисунок).
Формула объема шара
V=4πR³/3
Формула объема конуса
V=πr²h/3
1) Вычислим объем конуса, подставив в формулу радиус и высоту, выраженные через R.
2) Разделив выражение объема шара на найденный объем конуса, вычислим во сколько раз объем шара больше объема данного конуса.
3) Умножив 6 ( объем конуса) на число отношения объемов, получим объем шара.
Вычисления даны в приложении.
Результат:
объем шара равен 192*(2-√3) или ≈51,446 (ед. объема)

Hihit
+16
Решено
6 лет назад
Геометрия
10 – 11 классы
Конус вписан в шар, радиус основания конуса равен радиуса шара. Объем конуса равен 2. Найдите объем шара
Смотреть ответ
1
Ответ
4
(4 оценки)
1

Noorа
6 лет назад
Светило науки – 135 ответов – 536 раз оказано помощи
Если радиусы основания и шара равны, значит основание конуса проходит строго по центру шара
Объем конуса 1/3πR²H, в данном случае Н=R,значит объем конуса =1/3πR³
Объем шара =4/3πR³ то есть в 4 раза больше чем объем конуса, значит объем шара = 2*4=8
(4 оценки)
https://vashotvet.com/task/3956597
