Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас
слышал про эту знаменитую спортивную игру. Всем известно,
что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть
людей скажут, что форму шара, а часть, что формы сферы. Так кто же
из них прав? И в чем разница между сферой и шаром?
Важно!

Шар — это пространственное тело. Внутри шар
чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.
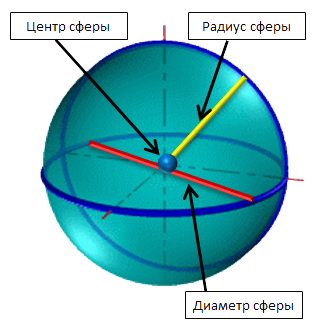
Важно!

Сфера — поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.
Как найти площадь сферы
Запомните!
![]()
Формула площади сферы:
S = 4πR2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа.
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π R2 =
4πR · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
-
Вычислите площадь сферы, если её радиус равен
1 м. (возьмите π как
3)
Вспомнив, как выделить целую часть
и перемножить дроби,
воспользуемся формулой площади сферы:
S = 4 · πR2 =
4 · 3 ·
(1 ) 2 =
4 · ·
() 2 =
4 · ·
=
=
= =
=
=
45
м2
Как найти объем шара
Запомните!
![]()
- Формула объема шара:
V = πR3
Зная определение степени,
можно записать формулу объема шара следующим образом.
-
V =
π R3 =π R · R · R;
Для отработки полученных знаний решим задачу на объем шара.
Зубарева 6 класс. Номер 691(а)
Условие задачи:
-
Вычислите радиус шара, если его объем равен
4 м3 (возьмите π как
3)
Выразим из формулы объема шара радиус.
- V =
π R3 -
π R3
= V -
π R3
=
-
R3
=
Подставим в формулу известные нам значения. Число π
возьмем как задано в задании «3».
R3
= (3 ·
4) /
(4 · 3)
Чтобы не запутаться, отдельно рассчитаем
числитель дроби.
3 ·
4 =
3 ·
=
=
Теперь снова подставим полученное значение в нашу формулу:
-
R3
=
/ (4 · 3)=
/ (4 · )
=
/ () =
=
· () =
= =
=
= 1
- R3 = 1
- R = 1 м
Важно!

Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень. Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст
единицу.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
14 февраля 2019 в 22:59
Руслан Магомедов

Профиль
Благодарили: 0
Сообщений: 1

Руслан Магомедов
Профиль
Благодарили: 0
Сообщений: 1
Рассчитайте объем чашки высотой 7 см с диаметром 6,5 с
0
Спасибо
Ответить
В данной публикации мы рассмотрим, как можно найти объем шара и разберем примеры решения задач для закрепления материала.
-
Формула вычисления объема шара
- Примеры задач
Формула вычисления объема шара
1. Через радиус
Объем (V) шара равняется четырем третьим произведения его радиуса в кубе и числа π.


Примечание: в расчетах значение числа π округляется до 3,14.
2. Через диаметр
Диаметр шара равняется двум его радиусам: d = 2R. А значит, формула вычисления объема может выглядеть следующим образом:

Примеры задач
Задание 1
Вычислите объем шара, если его радиус равняется 3 см.
Решение:
Применив первую формулу (через радиус) получаем:![]()
Задание 2
Найдите объем шара, если известно, что его диаметр равен 12 см.
Решение:
Используем вторую формулу, в которой задействован диаметр:![]()
|
Нужно знать его радиус. Умножить 4/3 на число “пи” и на радиус шара в третьей степени. К примеру, объем шара с радиусом 2 метра будет: 4/3х3,14х8=33,5 куб.метра автор вопроса выбрал этот ответ лучшим
Алиса в Стране 5 лет назад Все, что нам нужно для вычисления объема шара – это просто знать его радиус и нехитрую формулу для расчета. Формула вот такая:
Допустим, радиус нашего шара равен 10 сантиметрам, подставляем 10 см в нашу формулу и получаем: V = 4/3 х 3,14 х 1000 = 4187 кубических сантиметров.
Марина Вологда 5 лет назад Чтобы найти объем шара (сферы) следует знать его радиус или диаметр. Если радиус шара (сферы) известен, применяем следующую формулу:
Где “r” – радиус шара. Известно, что “Пи” всегда равно 3,14. Так же иногда в задачах дается диаметр шара (сферы). Если известен диаметр шара, применяется следующая формула:
Где “d” – это диаметр.
Любопытство 5 лет назад В выпускном, одиннадцатом (насколько я помню) классе учат находить объём шара вот так: высчитывают его по формуле: 4/3 Пи Х радиус в кубе. Думаю, что значение Пи всем известно, но на всякий случай сообщаю: π = 3,14.
В Рокотов 5 лет назад Сначала определимся что такое шар – это точки пространства равноудаленные от центра шара. Чтобы найти объем шара, при известном значении пи (3,14), нужно знать значения его радиуса или половины радиуса -диаметра, при известном радиусе искомое можно получить по формуле:
Zolotynka 5 лет назад Для начала разберемся, что представляет собой такая геометрическая фигура как шар. Итак, шар – это твердое тело, у которого есть особенность: любая точка на поверхности шара будет находиться на одном и том же расстоянии от его центра. Данное расстояние известно как радиус. Максимально прямое расстояние через центр шара принято называть диаметром. Диаметр -вдвое больше радиуса. Теперь посмотрим, как найти объем шара? Объем сферы равен четырем третям произведения числа pi и радиуса, возведенного в куб. Формула будет выглядеть следующим образом:
** Число pi, в задачах принято сокращать до двух десятых- 3,14.
Ninaarc 5 лет назад Шар представляет собой часть пространства, которое ограничено сферой. Для определения объема шара имеется специальная формула, в которую следует подставить нужные значения. Формула для вычисления объема шара выглядит таким образом:
Из формулы становится ясно, что нам должен быть известен радиус шара (r), который затем потребуется возвести в третью степень. А число ПИ нам хорошо известно, оно в числовом значении выглядит так: π = 3,14.
Трибунька 8 лет назад Чтобы вычислить объем шара надо знать формулу, где R – радиус шара.
Вот есть отличный сайт где можно онлайн высчитать объём шара. Этот сайт очень полезен для школьников, так как там много формул по геометрии, математике, физике и химии. Кроме формул некоторые задачи можно решить сразу на сайте. Есть справочные таблицы. Сайт очень удобно и грамотно сделан, все легко и просто на нём искать.
Нахождение объема шара, тема урока по Геометрии, если я не ошибаюсь, одиннадцатого класса общеобразовательной школы. Для нахождения объема геометрического тела Шар, нужно знать диаметр диаметр этого тела, разделив который на два получим его радиус. А далее подставляем это значение (радиус) в ниже приведенную формулу, и на выходе получаем объем шара.
РУДЬКО 5 лет назад Объём шара, это всем известная формула, которая на словах звучит как “четыре третьих пи эр в кубе”. То есть это проиизведение частного от 43 умноженное на число “Пи” и радиуса шара, возведённого в третью степень, то есть в “куб”.
vksvovko 6 лет назад 4/3*Пи*радиус в кубе. это и есть объем шара. Есть ещё один интересный способ – опустить его в измерительную емкость с водой, и сколько он вытеснит воды столько и его объем. таким способом можно измерять любой предмет. Знаете ответ? |

{V= dfrac{4}{3} pi R^3}
На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.
Шар – это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.
Содержание:
- калькулятор объема шара
- формула объема шара через радиус
- формула объема шара через диаметр
- формула объема шара через длину окружности
- формула объема шара через площадь поверхности
- примеры задач
Формула объема шара через радиус

{V = dfrac{4}{3} pi R^3}
R – радиус шара
Формула объема шара через диаметр
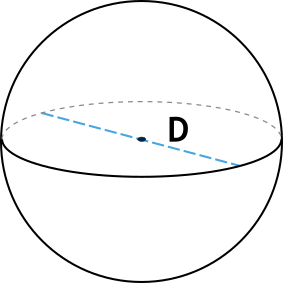
{V = dfrac{1}{6} pi D^3}
D – диаметр шара
Формула объема шара через длину окружности
Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2pi r}
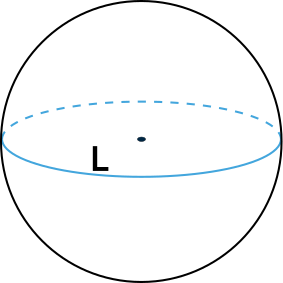
{V = dfrac{L^3}{6 pi^2}}
L – длина окружности
Формула объема шара через площадь поверхности
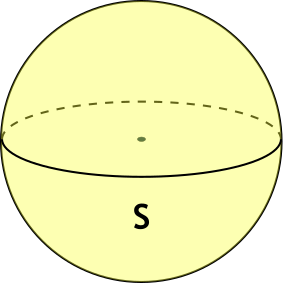
{V = sqrt{ dfrac{S^3}{36 pi}}}
S – площадь поверхности
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объем шара радиус которого равен 12см.
Решение
Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.
V = dfrac{4}{3} pi R^3 = dfrac{4}{3} pi cdot 12^3 = dfrac{4}{3} pi cdot 1728 = dfrac{4 cdot 1728}{3} pi = 2304 cdot pi : см^3 approx 7238.22947 : см^3
Ответ: 2304 cdot pi : см^3 approx 7238.22947 : см^3
Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .
Задача 2
Найдите объем шара диаметр которого равен 12см.
Решение
В этой задаче воспользуемся формулой шара через диаметр.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 12^3 = dfrac{1}{6} pi cdot 1728 = dfrac{1728}{6} pi = 288 pi : см^3 approx 904.77868 : см^3
Ответ: 288 pi : см^3 approx 904.77868 : см^3
И снова в проверке ответа нам поможет калькулятор .
Задача 3
Найдите объем шара диаметр которого равен 6см.
Решение
Эта задача аналогична задаче 2.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 6^3 = dfrac{1}{6} pi cdot 216 = dfrac{216}{6} pi = 36 pi : см^3 approx 113.09734 : см^3
Ответ: 36 pi : см^3 approx 113.09734 : см^3
И снова в проверке ответа нам поможет калькулятор .

Рис. (1). Футбольный мяч
Шар — это геометрическое тело.
Предметы, имеющие форму шара, окружают нас очень часто.
Форму шара имеет мяч (футбольный, теннисный, баскетбольный).
Представление о шаре дают арбуз, апельсин, горошина.
Шарообразна и наша планета Земля.
Шар характеризует длина радиуса и диаметра.

Рис. (2). Шар
Перед нами изображение шара с центром в точке (O). Все точки поверхности шара находятся на одинаковом расстоянии от его центра.
Это означает, что если мы выберем на поверхности три любые точки, например, точку (A), точку (B) и точку (C), соединим их с центром шара, то полученные отрезки будут равны ((OA = OB = OC)).
Такие отрезки называют радиусами.
(OA) — радиус шара, (OB) — радиус шара и (OC) — также радиус шара.
Так как центр шара можно соединить с бесконечно многими точками на поверхности шара, то можно провести бесконечно много радиусов.
Радиус шара — это отрезок, который соединяет точку поверхности шара и его центр.
На чертеже отрезок (AB) соединяет две точки поверхности шара и проходит через его центр.
Отрезок (AB) — это диаметр шара. Заметим, что отрезок (AB) состоит из двух отрезков (OA) и (OB).
Эти отрезки являются радиусами шара.
Поэтому диаметр шара в два раза больше его радиуса.
Диаметром шара называется отрезок, соединяющий две точки поверхности шара и проходящий через его центр.
Есть название и для поверхности шара. Её называют сферой.
Для шара можно вычислить объём по формуле:
Для сферы можно вычислить поверхность по формуле:
Источники:
Рис. 1. Футбольный мяч. Указание авторства не требуется, 2021.06.03, бесплатно для коммерческого использования,, https://pixabay.com/images/id-157930/
Рис. 2. Шар. © Якласс










