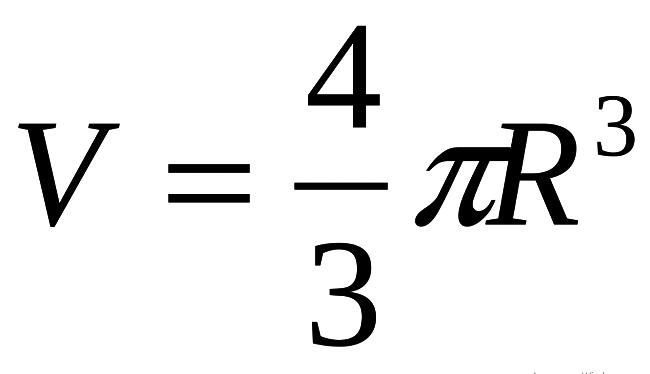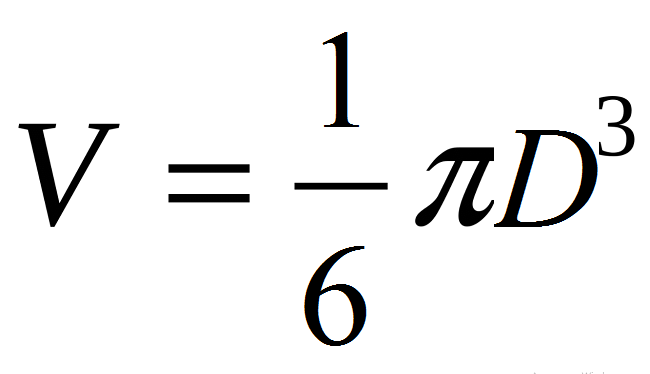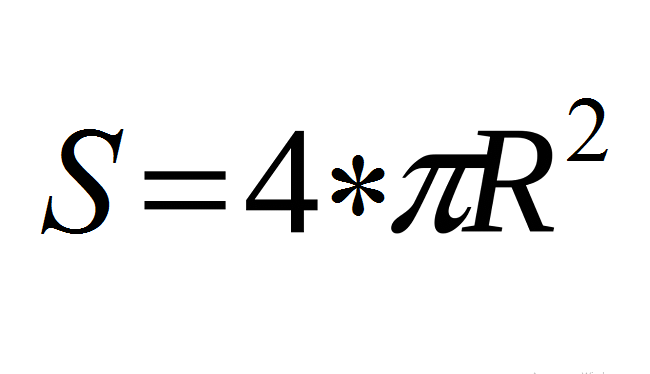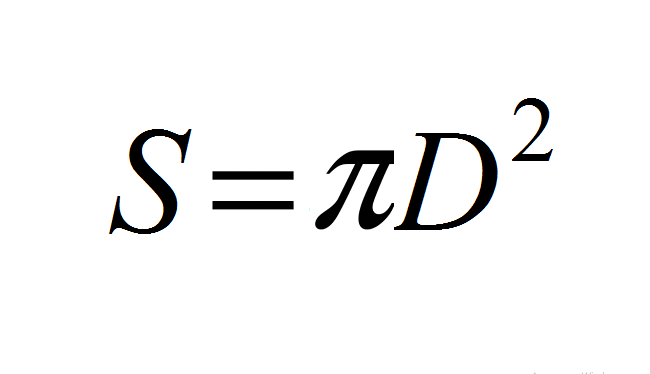В данной публикации мы рассмотрим, как можно найти объем шара и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема шара
- Примеры задач
Формула вычисления объема шара
1. Через радиус
Объем (V) шара равняется четырем третьим произведения его радиуса в кубе и числа π.
Примечание: в расчетах значение числа π округляется до 3,14.
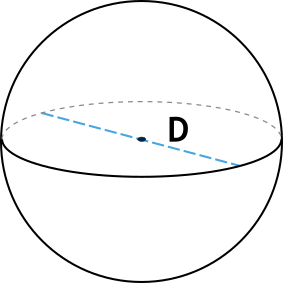
2. Через диаметр
Диаметр шара равняется двум его радиусам: d = 2R. А значит, формула вычисления объема может выглядеть следующим образом:
Примеры задач
Задание 1
Вычислите объем шара, если его радиус равняется 3 см.
Решение:
Применив первую формулу (через радиус) получаем:
Задание 2
Найдите объем шара, если известно, что его диаметр равен 12 см.
Решение:
Используем вторую формулу, в которой задействован диаметр:
|
Нужно знать его радиус. Умножить 4/3 на число “пи” и на радиус шара в третьей степени. К примеру, объем шара с радиусом 2 метра будет: 4/3х3,14х8=33,5 куб.метра автор вопроса выбрал этот ответ лучшим Алиса в Стране 5 лет назад Все, что нам нужно для вычисления объема шара – это просто знать его радиус и нехитрую формулу для расчета. Формула вот такая: Допустим, радиус нашего шара равен 10 сантиметрам, подставляем 10 см в нашу формулу и получаем: V = 4/3 х 3,14 х 1000 = 4187 кубических сантиметров. Марина Вологда 5 лет назад Чтобы найти объем шара (сферы) следует знать его радиус или диаметр. Если радиус шара (сферы) известен, применяем следующую формулу: Где “r” – радиус шара. Известно, что “Пи” всегда равно 3,14. Так же иногда в задачах дается диаметр шара (сферы). Если известен диаметр шара, применяется следующая формула: Где “d” – это диаметр. Любопытство 5 лет назад В выпускном, одиннадцатом (насколько я помню) классе учат находить объём шара вот так: высчитывают его по формуле: 4/3 Пи Х радиус в кубе. Думаю, что значение Пи всем известно, но на всякий случай сообщаю: π = 3,14. В Рокотов 5 лет назад Сначала определимся что такое шар – это точки пространства равноудаленные от центра шара. Чтобы найти объем шара, при известном значении пи (3,14), нужно знать значения его радиуса или половины радиуса -диаметра, при известном радиусе искомое можно получить по формуле: Zolotynka 5 лет назад Для начала разберемся, что представляет собой такая геометрическая фигура как шар. Итак, шар – это твердое тело, у которого есть особенность: любая точка на поверхности шара будет находиться на одном и том же расстоянии от его центра. Данное расстояние известно как радиус. Максимально прямое расстояние через центр шара принято называть диаметром. Диаметр -вдвое больше радиуса. Теперь посмотрим, как найти объем шара? Объем сферы равен четырем третям произведения числа pi и радиуса, возведенного в куб. Формула будет выглядеть следующим образом: ** Число pi, в задачах принято сокращать до двух десятых- 3,14. Ninaarc 5 лет назад Шар представляет собой часть пространства, которое ограничено сферой. Для определения объема шара имеется специальная формула, в которую следует подставить нужные значения. Формула для вычисления объема шара выглядит таким образом: Из формулы становится ясно, что нам должен быть известен радиус шара (r), который затем потребуется возвести в третью степень. А число ПИ нам хорошо известно, оно в числовом значении выглядит так: π = 3,14. Трибунька 8 лет назад Чтобы вычислить объем шара надо знать формулу, где R – радиус шара. Вот есть отличный сайт где можно онлайн высчитать объём шара. Этот сайт очень полезен для школьников, так как там много формул по геометрии, математике, физике и химии. Кроме формул некоторые задачи можно решить сразу на сайте. Есть справочные таблицы. Сайт очень удобно и грамотно сделан, все легко и просто на нём искать. Нахождение объема шара, тема урока по Геометрии, если я не ошибаюсь, одиннадцатого класса общеобразовательной школы. Для нахождения объема геометрического тела Шар, нужно знать диаметр диаметр этого тела, разделив который на два получим его радиус. А далее подставляем это значение (радиус) в ниже приведенную формулу, и на выходе получаем объем шара. РУДЬКО 5 лет назад Объём шара, это всем известная формула, которая на словах звучит как “четыре третьих пи эр в кубе”. То есть это проиизведение частного от 43 умноженное на число “Пи” и радиуса шара, возведённого в третью степень, то есть в “куб”. vksvovko 6 лет назад 4/3*Пи*радиус в кубе. это и есть объем шара. Есть ещё один интересный способ – опустить его в измерительную емкость с водой, и сколько он вытеснит воды столько и его объем. таким способом можно измерять любой предмет. Знаете ответ? |

{V= dfrac{4}{3} pi R^3}
На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.
Шар – это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.
Содержание:
- калькулятор объема шара
- формула объема шара через радиус
- формула объема шара через диаметр
- формула объема шара через длину окружности
- формула объема шара через площадь поверхности
- примеры задач
Формула объема шара через радиус
{V = dfrac{4}{3} pi R^3}
R – радиус шара
Формула объема шара через диаметр
{V = dfrac{1}{6} pi D^3}
D – диаметр шара
Формула объема шара через длину окружности
Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2pi r}
{V = dfrac{L^3}{6 pi^2}}
L – длина окружности
Формула объема шара через площадь поверхности
{V = sqrt{ dfrac{S^3}{36 pi}}}
S – площадь поверхности
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объем шара радиус которого равен 12см.
Решение
Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.
V = dfrac{4}{3} pi R^3 = dfrac{4}{3} pi cdot 12^3 = dfrac{4}{3} pi cdot 1728 = dfrac{4 cdot 1728}{3} pi = 2304 cdot pi : см^3 approx 7238.22947 : см^3
Ответ: 2304 cdot pi : см^3 approx 7238.22947 : см^3
Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .
Задача 2
Найдите объем шара диаметр которого равен 12см.
Решение
В этой задаче воспользуемся формулой шара через диаметр.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 12^3 = dfrac{1}{6} pi cdot 1728 = dfrac{1728}{6} pi = 288 pi : см^3 approx 904.77868 : см^3
Ответ: 288 pi : см^3 approx 904.77868 : см^3
И снова в проверке ответа нам поможет калькулятор .
Задача 3
Найдите объем шара диаметр которого равен 6см.
Решение
Эта задача аналогична задаче 2.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 6^3 = dfrac{1}{6} pi cdot 216 = dfrac{216}{6} pi = 36 pi : см^3 approx 113.09734 : см^3
Ответ: 36 pi : см^3 approx 113.09734 : см^3
И снова в проверке ответа нам поможет калькулятор .
Статья будет полезна школьникам и будущим абитуриентам, которые готовятся к сдаче ЕГЭ.
Содержание
- Формула объема шара через радиус: значение
- Формула объема шара через диаметр: значение
- Примеры вычисления объема шара, через радиус и диаметр шара: описание
- Формула полной поверхности шара, сферы через радиус: значение
- Формула полной поверхности шара, сферы через диаметр: значение
- Примеры вычисления площади поверхности, сферы шара, через радиус и диаметр шара: описание
- Как найти объем шара через площадь поверхности шара, сферы: пример решения задачи
- Видео: ЕГЭ математика. Объем и площадь поверхности тел вращения.
Формула объема шара через радиус: значение
Объем шара V вычисляется по формуле (см. ниже), где R — радиус шара, число «пи» — π — математическая константа, ≈ 3,14.
Данная формула является базовой!
Формула объема шара через диаметр: значение
- Воспользуйтесь базовой формулой: V=4/3*π*R³.
- Радиус R — это ½ диаметра D или R=D/2.
- Отсюда: V=4/3*π*R³ → V=(4π/3)*(D/2)³ → V=(4π/3)*(D³/8)→ V= πD³/6.
Или
Примеры вычисления объема шара, через радиус и диаметр шара: описание
Задача 1.
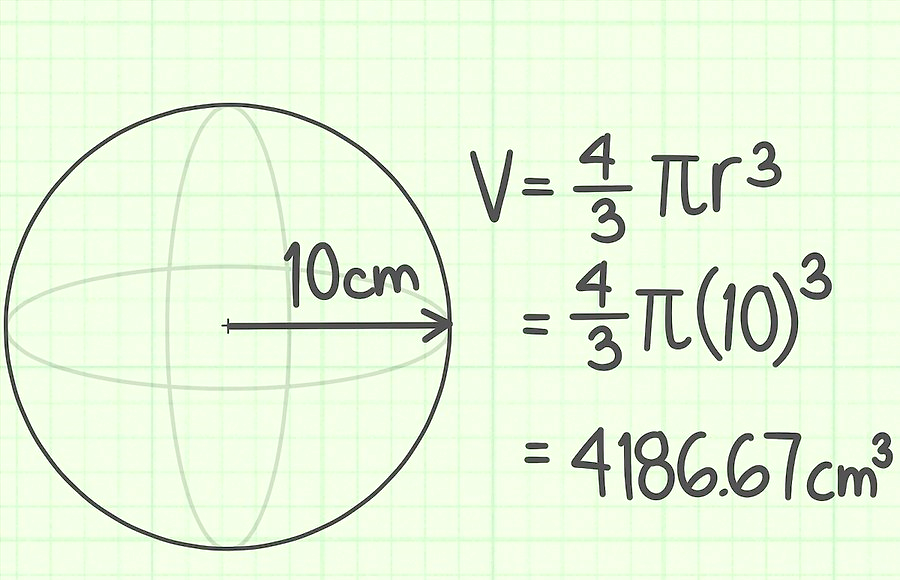
Радиус шара равен 10 см. Найди его объем.
Задача 2.
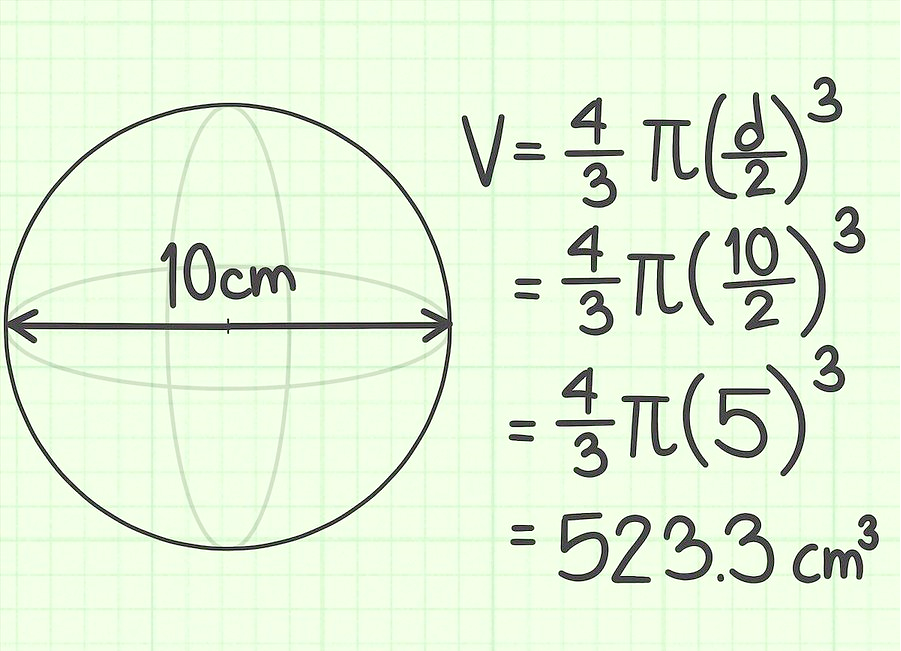
Диаметр шара равен 10 см. Найди его объем.
Задача 3.
Соотношение диаметра Луны и диаметра Земли 1:4. Во сколько раз объем Земли больше объема Луны?
Решение:
Ответ: в 64 раза.
Важно: существует множество онлайн калькуляторов, позволяющих быстро найти заданную величину. Например, сервис Webmath.
Формула полной поверхности шара, сферы через радиус: значение
Площадь поверхности сферы/шара S вычисляется по формуле (см. ниже), где R — радиус шара, число «пи» — π — математическая константа, ≈ 3,14.
Данная формула является базовой!
Формула полной поверхности шара, сферы через диаметр: значение
- Воспользуйтесь базовой формулой: S = 4*π*R².
- Радиус R — это ½ диаметра D или R=D/2.
- Отсюда: S=4*π*R² → S=4*π*(D/2)² → S=(4π)*(D²/4)→ S = (4πD²)/4 → S = πD².
Или
Примеры вычисления площади поверхности, сферы шара, через радиус и диаметр шара: описание
Задача 4.
Задача 5.
Задача 6.
Как найти объем шара через площадь поверхности шара, сферы: пример решения задачи
Задача 7.
Задача 8.
Видео: ЕГЭ математика. Объем и площадь поверхности тел вращения.
Как найти объем шара
Шар, он же сфера, нечасто встречаемая в геометрии фигура, но умение находить ее объем необходимо, так как вычисления с шаром часто являются вспомогательным процессом геометрической задачи.
1
Как найти объем шара
Для того чтобы найти объем шара применяется формула: V = 4/3*π*R³, где V – объем сферы, π – постоянное число, равное 3.14159 (≈3.14), а R – радиус шара. Для нахождения объема достаточно знать всего-лишь радиус шара.
Пример 1:
- Найти объем шара, если R = 7 см.
- Подставляем значение в формулу: V = 4/3×π×R³ => 4/3×3,14×7³ ≈ 1437 см³
- Может также встретиться задача, где объем известен, а радиус – нет. В такой задаче следует вывести формулу нахождения радиуса через формулу объема: V = 4/3×π×R³ => R³ = V/4/3×π.
Пример 2:
- Найти радиус шара, если объем равен 1437 см³.
- Выводим формулу радиуса: V = 4/3×π×R³ => R³ = V/(4/3×π).
- Подставляем значения: R³ = 1437/(4/3×3.14) ≈ 7.
2
Как найти объем шара онлайн
Если радиус шара больше 10, то возводить число в третью степень бывает неудобно. В таких случаях для нахождения объема можно воспользоваться данным сервисом. Просто впишите значение радиуса и мини-калькулятор выдаст вам правильный ответ.