Объём шара
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём шара
Чтобы посчитать объём шара, ограниченного сферой, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Чему равен объём шара, если:
=
Vшара =
0
Округление числа π: Округление ответа:
Чему равен объём шара, если:
Площадь поверхности шара Sпов =
Vшара =
0
Округление числа π: Округление ответа:
Просто введите данные, и получите ответ.
Теория
Объём шара через радиус
Чему равен объём шара Vшара, если его радиус r?
Формула
Vшара = 4⁄3 ⋅ π ⋅ r³ , где π ≈ 3.14…
Пример
Для примера посчитаем чему равен объём шара в кубических сантиметрах, если его радиус r = 2 см:
Vшара = 4/3 ⋅ 3.14 ⋅ 2³ = 4/3 ⋅ 3.14 ⋅ 8 = 100.48/3 ≈ 33.493 см³
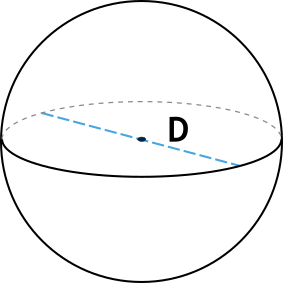
Объём шара через диаметр
Чему равен объём шара Vшара, если его диаметр d?
Формула
Vшара = 1⁄6 ⋅ π ⋅ d³
Пример
Для примера посчитаем чему равен объём шара в кубических метрах, если его диаметр d = 0.5 м:
Vшара = 1/6 ⋅ π ⋅ 0.5³ = (3.14 ⋅ 0.125) / 6 ≈ 0.0654 м³
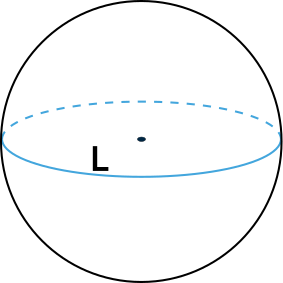
Объём шара через длину окружности
Чему равен объём шара Vшара, если длина его окружности L?
Формула
Vшара = L³⁄6π²
Пример
Для примера посчитаем чему равен объём шара в кубических миллиметрах, если длина окружности у него L = 50 мм:
Vшара = 50³ ⁄ 6 ⋅ 3.14² = 125000 / 59.1576 ≈ 2113 мм³
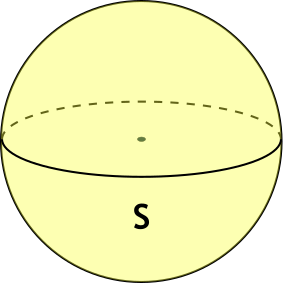
Объём шара через площадь поверхности шара
Чему равен объём шара Vшара, если площадь его поверхности Sпов?
Формула
Пример
Для примера посчитаем чему равен объём шара в кубических сантиметрах, если площадь поверхности у него Sпов = 225 см²:
Vшара = √ 225³ ⁄ (36 ⋅ 3.14) = √ 11390625 ⁄ 113.04 = √ 11390625 ⁄ 113.04 ≈ 317.44 см³
См. также

{V= dfrac{4}{3} pi R^3}
На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.
Шар – это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.
Содержание:
- калькулятор объема шара
- формула объема шара через радиус
- формула объема шара через диаметр
- формула объема шара через длину окружности
- формула объема шара через площадь поверхности
- примеры задач
Формула объема шара через радиус
{V = dfrac{4}{3} pi R^3}
R – радиус шара
Формула объема шара через диаметр
{V = dfrac{1}{6} pi D^3}
D – диаметр шара
Формула объема шара через длину окружности
Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2pi r}
{V = dfrac{L^3}{6 pi^2}}
L – длина окружности
Формула объема шара через площадь поверхности
{V = sqrt{ dfrac{S^3}{36 pi}}}
S – площадь поверхности
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объем шара радиус которого равен 12см.
Решение
Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.
V = dfrac{4}{3} pi R^3 = dfrac{4}{3} pi cdot 12^3 = dfrac{4}{3} pi cdot 1728 = dfrac{4 cdot 1728}{3} pi = 2304 cdot pi : см^3 approx 7238.22947 : см^3
Ответ: 2304 cdot pi : см^3 approx 7238.22947 : см^3
Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .
Задача 2
Найдите объем шара диаметр которого равен 12см.
Решение
В этой задаче воспользуемся формулой шара через диаметр.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 12^3 = dfrac{1}{6} pi cdot 1728 = dfrac{1728}{6} pi = 288 pi : см^3 approx 904.77868 : см^3
Ответ: 288 pi : см^3 approx 904.77868 : см^3
И снова в проверке ответа нам поможет калькулятор .
Задача 3
Найдите объем шара диаметр которого равен 6см.
Решение
Эта задача аналогична задаче 2.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 6^3 = dfrac{1}{6} pi cdot 216 = dfrac{216}{6} pi = 36 pi : см^3 approx 113.09734 : см^3
Ответ: 36 pi : см^3 approx 113.09734 : см^3
И снова в проверке ответа нам поможет калькулятор .
Калькулятор для расчета объема шара
C помощью нашего Онлайн-калькулятора для расчета объема шара Вы можете быстро и точно рассчитать объем шара. Для того, чтобы вычислить объем шара, введите значение радиуса шара “R” и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем шара.

Задайте значение радиуса шара R и нажмите кнопку “Рассчитать”
R =
Округлить результат до
знаков после запятой
Рассчитать
Шар – это геометрическое тело, ограниченного поверхностью, все точки которой находятся на одинаковом расстоянии от центра шара. Это расстояние называется радиусом шара.
Объем шара вычисляется по следующей формуле:
,
где R – радиус шара.
Главная
-
- 0
-
Радиус шара 3/4 дм. вычислите с точностью до сотых обьем шара в кубических дециметрах и площадь сферы в квадратных дециметрах
Лия Минхина
Вопрос задан 1 октября 2019 в
5 – 9 классы,
Математика.
-
Комментариев (0)
Добавить
Отмена
1 Ответ (-а, -ов)
- По голосам
- По дате
-
- 0
-
Объем шара по формуле
V = 4/3*π*R³ = 3.14* 4/3*27/64 ≈ 1.766 ≈ 1.77 дм³ — ОТВЕТ
Площадь сферы по формуле
S = 4*π*R² = 4*3.14*9/16 = 9/4*π ≈ 7.065 ≈ 7.07 дм² — ОТВЕТ
Отмена
Иван Седаметов
Отвечено 1 октября 2019
-
Комментариев (0)
Добавить
Отмена
Ваш ответ
Шар — это тело, все точки которого находятся от заданой точки на расстоянии, не превышающем R.
Онлайн-калькулятор объема шара
Заданная точка, о которой говорится в определении шара называется центром этого шара. А упомянутое расстояние — радиусом данного шара.
У шара, по аналогии с кругом, так же есть диаметр DD, который по длине в два раза больше радиуса:
D=2⋅RD=2cdot R
Формула объема шара через его радиус
Объем шара вычисляется по следующей формуле:
V=43⋅π⋅R3V=frac{4}{3}cdotpicdot R^3
RR — радиус данного шара.
Рассмотрим несколько примеров.
Шар вписан в куб, диагональ dd которого равна 500 см.sqrt{500}text{ см.} Найти объем шара.
Решение
d=500d=sqrt{500}
Для начала необходимо определить длину стороны куба. Будем считать, что она равна aa. Следовательно, диагональ куба, равна (исходя из теоремы Пифагора):
d=a2+a2+a2d=sqrt{a^2+a^2+a^2}
d=3⋅a2d=sqrt{3cdot a^2}
d=3⋅ad=sqrt{3}cdot a
500=3⋅asqrt{500}=sqrt{3}cdot a
a=5003a=sqrt{frac{500}{3}}
a≈12.9aapprox12.9
Если в куб вписан шар, то его радиус равен половинке длины стороны этого куба. В результате имеем:
R=12⋅aR=frac{1}{2}cdot a
R=12⋅12.9≈6.4R=frac{1}{2}cdot 12.9approx6.4
Заключительный этап — нахождение объема шара по формуле:
V=43⋅π⋅R3≈43⋅π⋅(6.4)3≈1097,5 см3V=frac{4}{3}cdotpicdot R^3approxfrac{4}{3}cdotpicdot (6.4)^3approx1097,5text{ см}^3
Ответ
1097,5 см3.1097,5text{ см}^3.
Формула объема шара через его диаметр
Так же объем шара можно найти через его диаметр. Для этого используем связь между радиусом и диаметром шара:
D=2⋅RD=2cdot R
R=D2R=frac{D}{2}
Подставим это выражение в формулу для объема шара:
V=43⋅π⋅R3=43⋅π⋅(D2)3=π6⋅D3V=frac{4}{3}cdotpicdot R^3=frac{4}{3}cdotpicdotBig(frac{D}{2}Big)^3=frac{pi}{6}cdot D^3
V=π6⋅D3V=frac{pi}{6}cdot D^3
DD — диаметр данного шара.
Диаметр шара равен 15 см.15text{ см.} Найдите его объем.
Решение
D=15D=15
Сразу подставляем значение диаметра в формулу:
V=π6⋅D3=π6⋅153≈1766.25 см3V=frac{pi}{6}cdot D^3=frac{pi}{6}cdot 15^3approx1766.25text{ см}^3
Ответ
1766.25 см3.1766.25text{ см}^3.
Не знаете, где оформить выполнение контрольных работ на заказ? Профильные эксперты Студворк помогут вам с решением!