Чтобы легко справиться с решением задач на шар, вписанный в пирамиду, полезно разобрать небольшой теоретический материал.
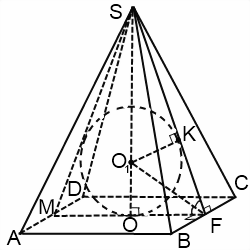
Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения бисекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).
Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды.
Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.
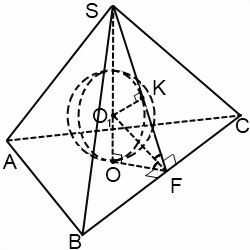
Если пирамида треугольная или пятиугольная, достаточно рассмотреть лишь часть этого сечения — прямоугольный треугольник, катеты которого — высота пирамиды и радиус вписанной в основание пирамиды окружности, а гипотенуза — апофема.
В любом случае, в итоге приходим к рассмотрению соответствующего прямоугольного треугольника и других связанных с ним треугольников.
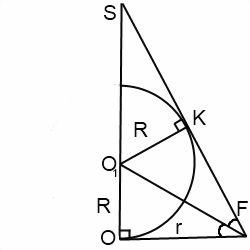
Прямоугольные треугольники OO1F и KO1F равны (по катетам и гипотенузе). Отсюда KF=OF=r.
Прямоугольные треугольники SKO1 и SOF подобны (по острому углу S), откуда следует, что
В треугольнике SOF применим свойство биссектрисы треугольника:
Из прямоугольного треугольника OO1F
При решении задач на шар, вписанный в правильную пирамиду, будет полезным еще одно рассуждение.
Теперь найдем отношение объема пирамиды к площади ее поверхности:
Таким образом, радиус вписанного шара выражается через объем пирамиды и ее полную поверхность:
Все эти рассуждения верны не только для правильной пирамиды, но и для пирамиды, основание высоты которой совпадает с центром вписанной в основание окружности (то есть для пирамиды, у которой все двугранные углы при основании равны).
Задания
Версия для печати и копирования в MS Word
Тип C10 № 660
i
Найдите объем шара, вписанного в треугольную пирамиду, все ребра которой равны см.
Спрятать решение
Решение.
Пусть шар с центром в точке О вписан в треугольную пирамиду. Тогда отрезок МО — биссектриса треугольника PMH. Точка H — центр треугольника ABC, тогда
Апофема PM — высота треугольника PBC, поэтому
По теореме Пифагора в треугольнике PMH:
Воспользуемся теоремой о биссектрисе угла в треугольнике HPM:
Найдем объем шара:
Ответ:
Классификатор геометрии: 3.4 Сфера и шар, их свойства, 3.6 Объемы круглых тел (0)
Спрятать решение
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Правильная треугольная пирамида и вписанный в эту пирамиду шар. Как найти объем вписанного в пирамиду шара?
Мастер
(2010),
закрыт
11 лет назад
п п
Мудрец
(10539)
13 лет назад
Рассмотрите осевое сечение пирамиды, получите треурольник с вписанной окружностью оттуда вычислите радиус, а по радиусу объем.
LeonidВысший разум (388685)
13 лет назад
На осевом сечении окружность НЕ БУДЕТ вписана в треугольник – она касается граней, но не рёбер. Сечение для этого надо будет взять не плоским, а изломанным, примерно как на чертежах сложных деталей.
В данной публикации представлены формулы, с помощью которых можно найти радиус шара (сферы), вписанного в правильную пирамиду: треугольную, четырехугольную, шестиугольную и тетраэдр.
-
Формулы расчета радиуса шара (сферы)
- Правильная треугольная пирамида
- Правильная четырехугольная пирамида
- Правильная шестиугольная пирамида
Формулы расчета радиуса шара (сферы)
Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.
Правильная треугольная пирамида
На рисунке:
- a – ребро основания пирамиды, т.е. это равные отрезки AB, AC и BC;
- DE – высота пирамиды (h).
Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:
Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:
Правильная четырехугольная пирамида
На рисунке:
- a – ребро основания пирамиды, т.е. AB, BC, CD и AD;
- EF – высота пирамиды (h).
Радиус (r) вписанного шара/сферы рассчитывается так:
Правильная шестиугольная пирамида
На рисунке:
- a – ребро основания пирамиды, т.е. AB, BC, CD, DE, EF, AF;
- GL – высота пирамиды (h).
Радиус (r) вписанного шара/сферы вычисляется по формуле:
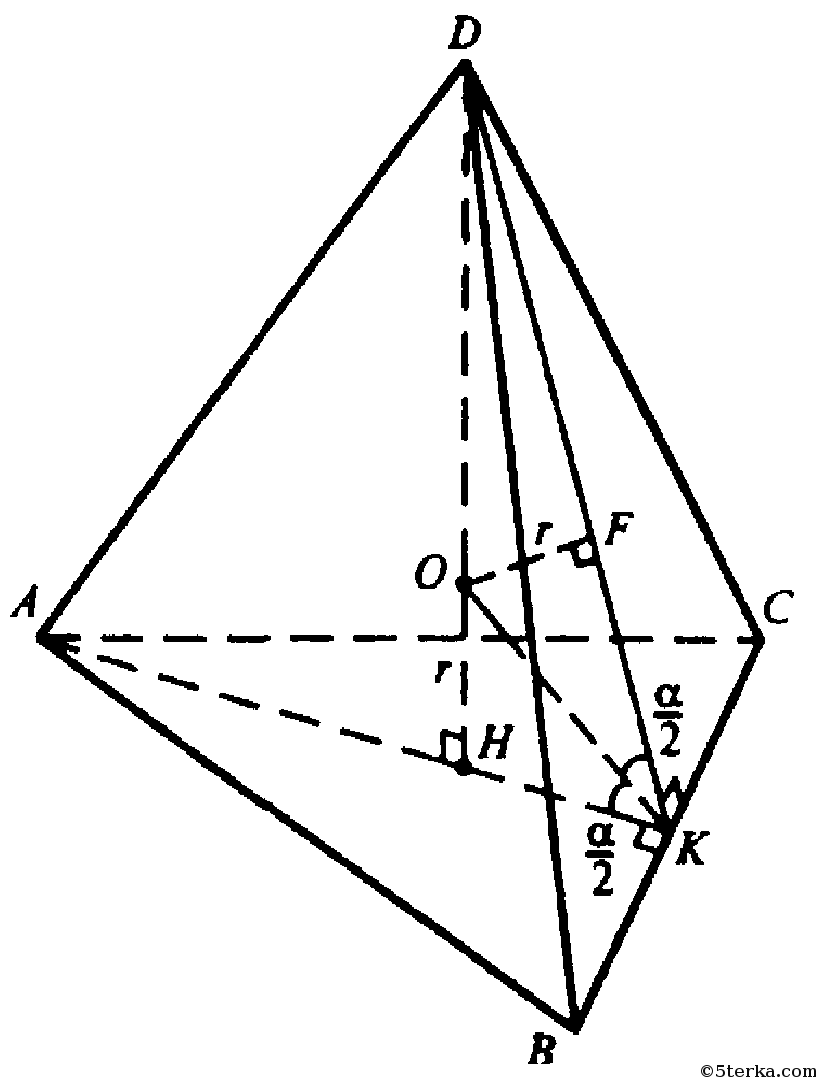
Через основание высоты DH построим АК⊥ВС, отрезок DK. По теореме о трех перпендикулярах DK перпендикулярно BC.
Центр вписанного шара находится на высоте пирамиды в точке О; ОН и OF — радиусы, равные r. По условию задачи
поэтому
Т.к. АК⊥ВС и DK⊥ВС, то ∠AKD — линейный угол двугранного угла при основании пирамиды.
∠AKD=α. ОК — биссектриса ∠DKA. Из равенства (ΔOHK=ΔOFK),
Обозначим сторону основания пирамиды за а. В равностороннем треугольнике АВС — НК это радиус вписанной окружности и
Из прямоугольного треугольника ОНК:
В треугольнике DHK: