Как найти объем шарика физика

Как найти объем шарика физика

В данной публикации мы рассмотрим, как можно найти объем шара и разберем примеры решения задач для закрепления материала.

  • Формула вычисления объема шара

  • Примеры задач

Формула вычисления объема шара

1. Через радиус

Объем (V) шара равняется четырем третьим произведения его радиуса в кубе и числа π.

Формула объема шара через радиус

Объем шара

Примечание: в расчетах значение числа π округляется до 3,14.

2. Через диаметр

Диаметр шара равняется двум его радиусам: d = 2R. А значит, формула вычисления объема может выглядеть следующим образом:

Формула объема шара через диагональ

Примеры задач

Задание 1
Вычислите объем шара, если его радиус равняется 3 см.

Решение:
Применив первую формулу (через радиус) получаем:
Формула вычисления объема шара через радиус

Задание 2
Найдите объем шара, если известно, что его диаметр равен 12 см.

Решение:
Используем вторую формулу, в которой задействован диаметр:
Формула нахождения объема шара через радиус

Источник

Как найти объем шара? Давайте рассмотрим этот вопрос с точки зрения математиков, физиков и инженеров. Для примера возьмем этот маленький красненький шарик. Как найти объем шара?

Математический подход

Думаю, первым что всплывёт в памяти математика, при словосочетании “объем шара”, будет эта формула:

    [V=frac {4}{3} pi R^3]

Ну а если вы вдруг не всплывёт, то её всегда можно вывести через интеграл:

Вывод формулы объема шара через интеграл Объем шара

  1. Проводим ось ОХ через центр шара.
  2. Площадь произвольного сечения на расстоянии x от центра шара можно выразить как:

    3.     [S(x)=pi (R^2-x^2)]

  3. Если проинтегрировать эту функцию на промежутке от -R до R мы получим объем шара.

    [V=intlimits_{-R}^{R} S(x),dx =intlimits_{-R}^{R} pi (R^2-x^2),dx =]

    [= pi intlimits_{-R}^{R} R^2 ,dx - pi intlimits_{-R}^{R} x^2 ,dx = pi R^2 x Bigr|_{-R}^{R} - frac {pi x^3}{3} Bigr|_{-R}^{R} =]

    [= pi R^3 +pi R^3 - frac {pi R^3}{3} - frac {pi R^3}{3} = frac {4}{3} pi R^3]

Единственное, на практике выражать объем через радиус будет не всегда удобно. Радиус трудно измерить напрямую. Куда проще штангенциркулем измерить диаметр. Поэтому чтоб лишний раз не упражняться в делении на два, можно представить объем шара сразу через его диаметр:

    [V=frac {1}{6} pi D^3]

Физический подход

Если измерение диаметра представляется чем-то затруднительным, а штангенциркуль, в вашем представлении, это что-то связанное с тяжелой атлетикой, то возможно, физический способ придется вам по душе.

Все предельно просто. Погружаем шар в воду, и смотрим как изменится ее уровень. Соответственно объем шара будет равен объему вытесненной им воды.

Стоит отметить, что этот метод подарил нам Архимед, более двух тысяч лет назад, и подходит он для измерения объема не только шаров, но и любых других фигур. Главное, чтоб их можно было мочить воде.

Легенда об Архимеде

Согласно легенде, по приказу царя Гиерона, правителя Саракуз была изготовлена золотая корона, которую он хотел пожертвовать в храм. Но поступил донос, что корона не из чистого золота, и в нее подмешано серебро. Соответственно часть золота была украдена.

Разобраться так ли это на самом деле царь поручил Архимеду, а тот, в свою очередь, думая над этой задачей, отправился прямиком в баню. Там, залезая в ванну, он обратил внимание что при погружении его тела в воду ее уровень поднимается. Поняв, что делать, Архимед выскочил из этой бани и с криками “эврика” голышом побежал домой.

Погрузив в воду корону, Архимед определил её объём. Затем тем же методом он определил объемы золотого и серебренного слитков, имеющих ту же массу что и эта корона. Ну а из соотношений объемов он выяснил, что корона действительно содержала примеси серебра.

Инженерный подход

Ну и наконец, как находят объем маленьких красных шариков настоящие инженеры? Здесь на самом деле все еще проще чем у физиков. Берем соответствующую техническую документацию, и смотрим объем там.

Источник

Объем шара через радиус

{V= dfrac{4}{3} pi R^3}

На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.

Шар – это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.

Содержание:
  1. калькулятор объема шара
  2. формула объема шара через радиус
  3. формула объема шара через диаметр
  4. формула объема шара через длину окружности
  5. формула объема шара через площадь поверхности
  6. примеры задач

Формула объема шара через радиус

Объем шара через радиус

{V = dfrac{4}{3} pi R^3}

R – радиус шара

Формула объема шара через диаметр

Объем шара через диаметр

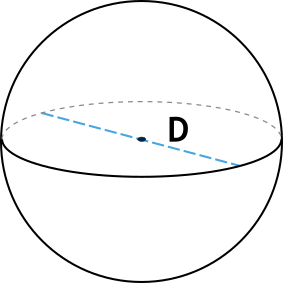
{V = dfrac{1}{6} pi D^3}

D – диаметр шара

Формула объема шара через длину окружности

Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2pi r}

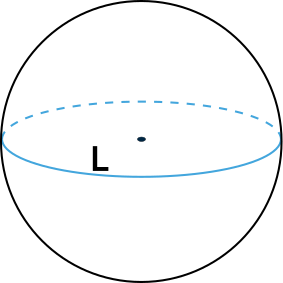
Объем шара через длину окружности

{V = dfrac{L^3}{6 pi^2}}

L – длина окружности

Формула объема шара через площадь поверхности

Объем шара через площадь поверхности

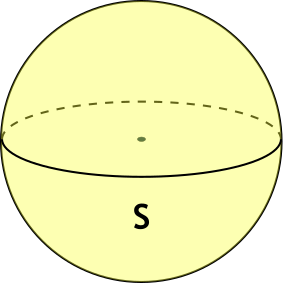
{V = sqrt{ dfrac{S^3}{36 pi}}}

S – площадь поверхности

Примеры задач на нахождение объема параллелепипеда

Задача 1

Найдите объем шара радиус которого равен 12см.

Решение

Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.

V = dfrac{4}{3} pi R^3 = dfrac{4}{3} pi cdot 12^3 = dfrac{4}{3} pi cdot 1728 = dfrac{4 cdot 1728}{3} pi = 2304 cdot pi : см^3 approx 7238.22947 : см^3

Ответ: 2304 cdot pi : см^3 approx 7238.22947 : см^3

Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .

Задача 2

Найдите объем шара диаметр которого равен 12см.

Решение

В этой задаче воспользуемся формулой шара через диаметр.

V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 12^3 = dfrac{1}{6} pi cdot 1728 = dfrac{1728}{6} pi = 288 pi : см^3 approx 904.77868 : см^3

Ответ: 288 pi : см^3 approx 904.77868 : см^3

И снова в проверке ответа нам поможет калькулятор .

Задача 3

Найдите объем шара диаметр которого равен 6см.

Решение

Эта задача аналогична задаче 2.

V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 6^3 = dfrac{1}{6} pi cdot 216 = dfrac{216}{6} pi = 36 pi : см^3 approx 113.09734 : см^3

Ответ: 36 pi : см^3 approx 113.09734 : см^3

И снова в проверке ответа нам поможет калькулятор .

Источник

Нужно знать его радиус. Умножить 4/3 на число “пи” и на радиус шара в третьей степени. К примеру, объем шара с радиусом 2 метра будет: 4/3х3,14х8=33,5 куб.метра

автор вопроса выбрал этот ответ лучшим

Алиса в Стран­е
[363K]

5 лет назад 

Все, что нам нужно для вычисления объема шара – это просто знать его радиус и нехитрую формулу для расчета. Формула вот такая:

Допустим, радиус нашего шара равен 10 сантиметрам, подставляем 10 см в нашу формулу и получаем: V = 4/3 х 3,14 х 1000 = 4187 кубических сантиметров.

Марин­а Волог­да
[294K]

5 лет назад 

Чтобы найти объем шара (сферы) следует знать его радиус или диаметр.

Если радиус шара (сферы) известен, применяем следующую формулу:

Где “r” – радиус шара.

Известно, что “Пи” всегда равно 3,14.

Так же иногда в задачах дается диаметр шара (сферы). Если известен диаметр шара, применяется следующая формула:

Где “d” – это диаметр.

Любоп­ытств­о
[135K]

5 лет назад 

В выпускном, одиннадцатом (насколько я помню) классе учат находить объём шара вот так: высчитывают его по формуле: 4/3 Пи Х радиус в кубе. Думаю, что значение Пи всем известно, но на всякий случай сообщаю: π = 3,14.

В Рокот­ов
[277K]

5 лет назад 

Сначала определимся что такое шар – это точки пространства равноудаленные от центра шара. Чтобы найти объем шара, при известном значении пи (3,14), нужно знать значения его радиуса или половины радиуса -диаметра, при известном радиусе искомое можно получить по формуле:

Zolot­ynka
[550K]

5 лет назад 

Для начала разберемся, что представляет собой такая геометрическая фигура как шар.

Итак, шар – это твердое тело, у которого есть особенность: любая точка на поверхности шара будет находиться на одном и том же расстоянии от его центра. Данное расстояние известно как радиус. Максимально прямое расстояние через центр шара принято называть диаметром. Диаметр -вдвое больше радиуса.

Теперь посмотрим, как найти объем шара?

Объем сферы равен четырем третям произведения числа pi и радиуса, возведенного в куб. Формула будет выглядеть следующим образом:

**

Число pi, в задачах принято сокращать до двух десятых- 3,14.

Ninaa­rc
[479K]

5 лет назад 

Шар представляет собой часть пространства, которое ограничено сферой. Для определения объема шара имеется специальная формула, в которую следует подставить нужные значения. Формула для вычисления объема шара выглядит таким образом:

Из формулы становится ясно, что нам должен быть известен радиус шара (r), который затем потребуется возвести в третью степень. А число ПИ нам хорошо известно, оно в числовом значении выглядит так: π = 3,14.

Трибу­нька
[54.9K]

8 лет назад 

Чтобы вычислить объем шара надо знать формулу, где R – радиус шара.

текст при наведении

текст при наведении

Вот есть отличный сайт где можно онлайн высчитать объём шара. Этот сайт очень полезен для школьников, так как там много формул по геометрии, математике, физике и химии.

Кроме формул некоторые задачи можно решить сразу на сайте. Есть справочные таблицы. Сайт очень удобно и грамотно сделан, все легко и просто на нём искать.

Нахождение объема шара, тема урока по Геометрии, если я не ошибаюсь, одиннадцатого класса общеобразовательной школы.

Для нахождения объема геометрического тела Шар, нужно знать диаметр диаметр этого тела, разделив который на два получим его радиус. А далее подставляем это значение (радиус) в ниже приведенную формулу, и на выходе получаем объем шара.

РУДЬК­О
[256K]

5 лет назад 

Объём шара, это всем известная формула, которая на словах звучит как “четыре третьих пи эр в кубе”. То есть это проиизведение частного от 43 умноженное на число “Пи” и радиуса шара, возведённого в третью степень, то есть в “куб”.

vksvo­vko
[1.6K]

6 лет назад 

4/3*Пи*радиус в кубе.

это и есть объем шара.

Есть ещё один интересный способ – опустить его в измерительную емкость с водой, и сколько он вытеснит воды столько и его объем. таким способом можно измерять любой предмет.

Знаете ответ?
Источник
Определение шара

Шар — это тело, все точки которого находятся от заданой точки на расстоянии, не превышающем R.

Онлайн-калькулятор объема шара

Заданная точка, о которой говорится в определении шара называется центром этого шара. А упомянутое расстояние — радиусом данного шара.

У шара, по аналогии с кругом, так же есть диаметр DD, который по длине в два раза больше радиуса:

D=2⋅RD=2cdot R

Формула объема шара через его радиус

Объем шара вычисляется по следующей формуле:

Формула объема шара через радиус

V=43⋅π⋅R3V=frac{4}{3}cdotpicdot R^3

RR — радиус данного шара.

Рассмотрим несколько примеров.

Задача 1

Шар вписан в куб, диагональ dd которого равна 500 см.sqrt{500}text{ см.} Найти объем шара.

Решение

d=500d=sqrt{500}

Для начала необходимо определить длину стороны куба. Будем считать, что она равна aa. Следовательно, диагональ куба, равна (исходя из теоремы Пифагора):

d=a2+a2+a2d=sqrt{a^2+a^2+a^2}

d=3⋅a2d=sqrt{3cdot a^2}

d=3⋅ad=sqrt{3}cdot a

500=3⋅asqrt{500}=sqrt{3}cdot a

a=5003a=sqrt{frac{500}{3}}

a≈12.9aapprox12.9

Если в куб вписан шар, то его радиус равен половинке длины стороны этого куба. В результате имеем:

R=12⋅aR=frac{1}{2}cdot a

R=12⋅12.9≈6.4R=frac{1}{2}cdot 12.9approx6.4

Заключительный этап — нахождение объема шара по формуле:

V=43⋅π⋅R3≈43⋅π⋅(6.4)3≈1097,5 см3V=frac{4}{3}cdotpicdot R^3approxfrac{4}{3}cdotpicdot (6.4)^3approx1097,5text{ см}^3

Ответ

1097,5 см3.1097,5text{ см}^3.

Формула объема шара через его диаметр

Так же объем шара можно найти через его диаметр. Для этого используем связь между радиусом и диаметром шара:

D=2⋅RD=2cdot R

R=D2R=frac{D}{2}

Подставим это выражение в формулу для объема шара:

V=43⋅π⋅R3=43⋅π⋅(D2)3=π6⋅D3V=frac{4}{3}cdotpicdot R^3=frac{4}{3}cdotpicdotBig(frac{D}{2}Big)^3=frac{pi}{6}cdot D^3

Объем шара через диаметр

V=π6⋅D3V=frac{pi}{6}cdot D^3

DD — диаметр данного шара.

Задача 2

Диаметр шара равен 15 см.15text{ см.} Найдите его объем.

Решение

D=15D=15

Сразу подставляем значение диаметра в формулу:

V=π6⋅D3=π6⋅153≈1766.25 см3V=frac{pi}{6}cdot D^3=frac{pi}{6}cdot 15^3approx1766.25text{ см}^3

Ответ

1766.25 см3.1766.25text{ см}^3.

Не знаете, где оформить выполнение контрольных работ на заказ? Профильные эксперты Студворк помогут вам с решением!

Тест по теме «Объем шара»

Источник

Добавить комментарий