В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем шарового слоя (среза шара), а также пример решения задачи для демонстрации их практического применения.
- Определение шарового слоя
- Формула для нахождения объема шарового слоя
- Пример задачи
Определение шарового слоя
Шаровый слой (или срез шара) – это часть шара, оставшаяся между двумя пересекающими его параллельными плоскостями. На рисунке ниже окрашен в желтый цвет.
- R – радиус шара;
- r1 – радиус первого основания среза;
- r2 – радиус второго основания среза;
- h – высота шарового слоя; перпендикуляр от центра первого основания до центра второго.
Формула для нахождения объема шарового слоя
Чтобы найти объем шарового слоя (среза шара), необходимо знать его высоту, а также радиусы двух его оснований.
Эта же формула может быть представлена слегка в другом виде:
Примечания:
- если вместо радиусов оснований (r1 и r2) известны их диаметры (d1 и d2), последние нужно поделить на 2 для получения соответствующих им радиусов.
- число π обычно округляется до 3,14.
Пример задачи
Найдите объем шарового слоя, если радиусы его оснований равны 3,4 см и 5,2 см, а высота составляет 2 см.
Решение
Все что нам нужно сделать в данном случае – это подставить известные значения в одну из формул, приведенных выше (в качестве примера выберем вторую):
Шаровой слой
Шар пересеченный двумя параллельными плоскостями
Шаровой слой — часть шара, ограниченная двумя параллельными плоскостями, пересекающими шар[1].
Содержание
- 1 Связанные определения
- 2 Свойства
- 3 Вариации и обобщения
- 4 См. также
- 5 Примечания
Связанные определения[править | править код]
- Основания шарового слоя — это сечения шара, образовавшиеся в результате пересечения шара двумя параллельными плоскостями.
- Высота шарового слоя — это расстояние между основаниями слоя.
Свойства[править | править код]
- Объём шарового слоя можно найти как разность объёма двух шаровых сегментов:
![V=pi left[H_{1}^{2}left(R-{frac {1}{3}}H_{1}right)-H_{2}^{2}left(R-{frac {1}{3}}H_{2}right)right],](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E)
где — объём шарового слоя, — высота большего шарового сегмента, — высота меньшего шарового сегмента, — радиус шара. - Площадь сферической части поверхности шарового слоя (так называемый сферический пояс) зависит только от высоты слоя и радиуса шара[2]:
![V=pi left[H_{1}^{2}left(R-{frac {1}{3}}H_{1}right)-H_{2}^{2}left(R-{frac {1}{3}}H_{2}right)right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/712362c23e11227c1a27cae915df947b03f8c0aa)
- где — площадь сферического пояса, — высота шарового слоя, — радиус шара.
Вариации и обобщения[править | править код]
- В физике под шаровым слоем часто понимают слой, ограниченный сферами радиуса и , для маленького . Объем шарового слоя в этом случае с точностью до O равен .
См. также[править | править код]
- Сферический слой
Примечания[править | править код]
- ↑ Мантуров О. В. и др. Словарь математических терминов. — М.: Просвещение, 1965. — С. 512.
- ↑ Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров. — М.: Советская энциклопедия, 1988. — С. 638.
Как рассчитать объем шарового слоя
На данной странице калькулятор поможет рассчитать объем шарового слоя онлайн. Для расчета задайте радиусы и высоту. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Шаровой слой — это часть шара, ограниченная двумя секущими параллельными плоскостями.
Через радиусы и высоту
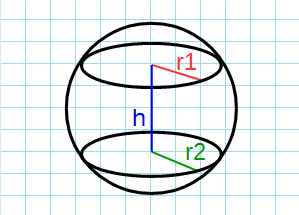
Формула объема шарового слоя через радиусы и высоту:
π – константа равная (3.14); r1 – радиус верхнего основания ; r2 – радиус нижнего основания; h – высота усеченного конуса.
Объем шарового слоя
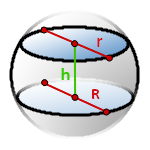
h– высота шарового слоя
R– радиус нижнего основания
r– радиус верхнего основания
π ≈ 3.14
Объем шарового слоя, (V):
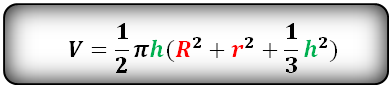
Калькулятор – вычислить, найти объем шарового слоя
- Подробности
-
Автор: Administrator
-
Опубликовано: 13 сентября 2011
-
Обновлено: 13 августа 2021
Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями. Для
вычисления объема шарового слоя достаточно знать радиусы кругов, ограничивающих шаровой слой, и
расстояние между ними (высота шарового слоя). Объем вычисляется по формуле:
V = (π / 6) * h * (3R² + 3r² + h²)
где R, r — радиусы, h — высота.
Цифр после
запятой:
Результат в:
Пример. Требуется найти объём шарового слоя зная что радиусы R = 3 см, r = 6 см,
высота h = 4 см. Подставим в формулу и получим: V = (3,14 / 6) * 4 * (3 * 3² + 3 * 6² + 4²) = 316 см³.
Примечательно, что для вычисления этого объема не требуется радиус самого шара. Требуются только
радиусы ограничивающих его кругов. Если секущие плоскости отодвинуть к полюсам шара, то высота h
станет равна диаметру шара, а радиусы кругов примут нулевые значения: R=0, r=0. Тогда формула примет
вид: V = π / 6 D³ = (4π / 3) * Rшара³. Это формула для вычисления объема
шара. Максимальный объем шарового слоя равен объему шара.
Актуально вычисление шарового слоя при устройстве сферических резервуаров, применяемых в химической
промышленности. Сферическая емкость применяется в тех случаях, когда давление в ней высокое.
Резервуар может иметь вид полной сферы или шарового слоя. Если в шаровом резервуаре находится
жидкость, заполняющая только часть объема, то по положению ее уровня можно определить высоту
шарового слоя и радиус ограничивающего круга, а потом посчитать объем жидкости. Сферические сосуды
используются и в быту. Примером может служить аквариум, выполненный в виде усеченного шара (шарового
слоя). Расчет его объема нужен для правильного оборудования среды обитания для аквариумных жителей.
Части конструкций в виде шарового слоя встречаются в машиностроении, архитектуре, столярном деле.
Вычисление объемов – необходимая часть конструкторской разработки.
