
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
Сайты, меню, вход, новости
Задания
Версия для печати и копирования в MS Word
Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны
и наклонены к плоскости основания под углом 30°.
Спрятать решение
Решение.
Объем призмы где S − площадь основания, а L − длина ребра, составляющего с основанием угол α. Площадь правильного шестиугольника со стороной a равна
Тогда объем призмы
Ответ: 18.
Найдите объём призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые рёбра равны 2√3 и наклонены к плоскости основания под углом 30°.
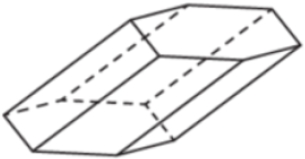
Источник: mathege
Решение:
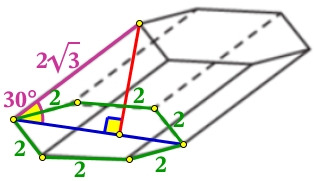
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы. Найдём высоту призмы, которая является катетом прямоугольного треугольника:
h=frac{2sqrt{3}}{2}=sqrt{3}
Найдём по формуле площадь основания призмы, правильный шестиугольник со сторонами 2:
S_{осн}=frac{3sqrt{3}}{2}cdot a^{2}=frac{3sqrt{3}}{2}cdot 2^{2}=6sqrt{3}
Найдём объём призмы:
Vпризмы = Sосн·h = 6√3·√3 = 6·3 = 18
Ответ: 18.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Определение объемов геометрических тел является одной из важных задач пространственной геометрии. В данной статье рассматривается вопрос, что такое призма с шестиугольным основанием, а также приводится формула объема правильной шестиугольной призмы.
Определение призмы
С точки зрения геометрии призмой называется фигура в пространстве, которая образована двумя одинаковыми многоугольниками, расположенными в параллельных плоскостях. А также несколькими параллелограммами, которые эти многоугольники соединяют в единую фигуру.
В трехмерном пространстве призму произвольной формы можно получить, если взять любой многоугольник и отрезок. Причем последний плоскости многоугольника принадлежать не будет. Тогда, располагая этот отрезок от каждой вершины многоугольника, можно получить параллельный перенос последнего в другую плоскость. Образованная таким способом фигура будет призмой.
Чтобы иметь наглядное представление о рассматриваемом классе фигур, приведем рисунок четырехугольной призмы.

Многие знают эту фигуру под названием параллелепипеда. Видно, что два одинаковых многоугольника призмы представляют собой квадраты. Их называют основаниями фигуры. Остальные четыре ее стороны – прямоугольники, то есть это частный случай параллелограммов.
Шестиугольная призма: определение и виды
Прежде чем приводить формулу, как определяется объем шестиугольной правильной призмы, необходимо четко понять, о какой фигуре пойдет речь. Шестиугольная призма имеет в основаниях шестиугольник. То есть, плоский многоугольник с шестью сторонами, углов столько же. Боковые стороны фигуры так же, как и для любой призмы, в общем случае являются параллелограммами. Сразу отметим, что шестиугольное основание может быть представлено как правильным, так и неправильным шестиугольником.
Расстояние между основаниями фигуры – это ее высота. Далее мы будем обозначать ее буквой h. Геометрически высота h представляет собой отрезок, перпендикулярный обоим основаниям. Если этот перпендикуляр:
- опущен с геометрического центра одного из оснований;
- пересекает второе основание также в геометрическом центре.
Фигура в этом случае называется прямой. В любом другом случае призма будет косоугольной или наклонной. Разницу между этими видами шестиугольной призмы можно увидеть с первого взгляда.
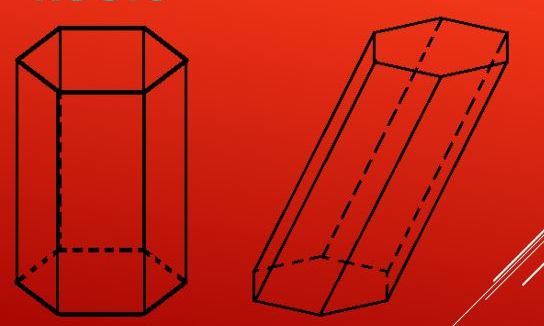
Прямая шестиугольная призма – это фигура, имеющая в основании правильные шестиугольники. При этом она является прямой. Рассмотрим подробнее ее свойства.
Элементы правильной шестиугольной призмы
Чтобы понять, как вычислить объем правильной шестиугольной призмы (формула приведена ниже в статье), необходимо также разобраться, из каких элементов состоит фигура, а также какими свойствами она обладает. Чтобы было легче анализировать фигуру, покажем ее на рисунке.

Главными ее элементами являются грани, ребра и вершины. Количества этих элементов подчиняется теореме Эйлера. Если обозначить Р – число ребер, В – количество вершин и Г – граней, тогда можно записать равенство:
Р = Г + В – 2.
Проверим его. Число граней рассматриваемой фигуры равно 8. Две из них – это правильные шестиугольники. Шесть граней представляет собой прямоугольники, это видно из рисунка. Число вершин составляет 12. Действительно, 6 вершин принадлежат одному основанию, и 6 другому. Согласно формуле, число ребер должно равняться 18, что является справедливым. 12 ребер лежат в основаниях и 6 образуют параллельные друг другу стороны прямоугольников.
Переходя к получению формулы объема правильной шестиугольной призмы, следует остановить свое внимание на одном важном свойстве этой фигуры: прямоугольники, образующие боковую поверхность, равны между собой и перпендикулярны обоим основаниям. Это приводит к двум важным следствиям:
- Высота фигуры равна длине ее бокового ребра.
- Любое сечение боковой поверхности пирамиды, выполненное с помощью секущей плоскости, которая параллельна основаниям, является правильным шестиугольником, равным этим основаниям.
Площадь шестиугольника
Можно интуитивно догадаться, что эта площадь основания фигуры появится в формуле объема правильной призмы шестиугольной. Поэтому в данном пункте статьи найдем эту площадь. Правильный шестиугольник, разделенный на 6 одинаковых треугольников, вершины которых пересекаются в его геометрическом центре, показан ниже:
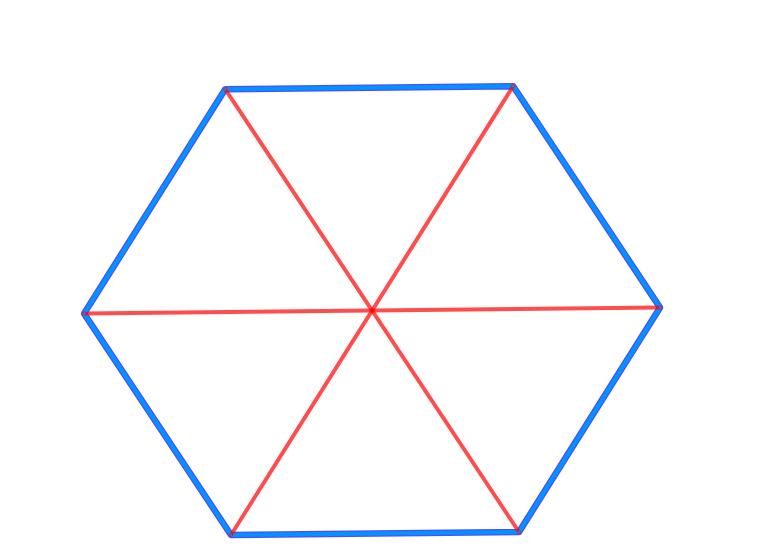
Каждый из этих треугольников является равносторонним. Доказать это не очень сложно. Поскольку вся окружность имеет 360o, то углы треугольников вблизи геометрического центра шестиугольника равны 360o/6=60o. Расстояния от геометрического центра до вершин шестиугольника являются одинаковыми.
Последнее означает, что все 6 треугольников будут равнобедренными. Поскольку один из углов равнобедренных треугольников равен 60o, значит, два остальных угла тоже равны по 60o. ((180o-60o)/2) – треугольники равносторонние.
Обозначим длину стороны шестиугольника буквой a. Тогда площадь одного треугольника будет равна:
S1 = 1/2*√3/2*a*a = √3/4*a2.
Формула получена на основании стандартного выражения для площади треугольника. Тогда площадь S6 для шестиугольника будет:
S6 = 6*S1 = 6*√3/4*a2 = 3*√3/2*a2.
Формула определения объема правильной шестиугольной призмы
Чтобы записать формулу для объема рассматриваемой фигуры, следует учесть приведенную выше информацию. Для произвольной призмы объем пространства, ограниченный ее гранями, вычисляется так:
V = h*So.
То есть, V равен произведению площади основания So на высоту h. Поскольку мы знаем, что высота h равна длине бокового ребра b для шестиугольной правильной призмы, а площадь ее основания соответствует S6, то формула объема правильной шестиугольной призмы примет вид:
V6 = 3*√3/2*a2*b.
Пример решения геометрической задачи
Дана шестиугольная правильная призма. Известно, что она вписана в цилиндр радиусом 10 см. Высота призмы в два раза больше стороны ее основания. Необходимо найти объем фигуры.

Чтобы найти требуемую величину, необходимо знать длину стороны и бокового ребра. При рассмотрении правильного шестиугольника было показано, что его геометрический центр расположен в середине описанной вокруг него окружности. Радиус последней равен расстоянию от центра до любой из вершин. То есть он равен длине стороны шестиугольника. Эти рассуждения приводят к следующим результатам:
a = r = 10 см;
b = h = 2*a = 20 см.
Подставляя эти данные в формулу объема правильной шестиугольной призмы, получим ответ: V6≈5196 см3 или около 5,2 литра.
