Содержание:
Сообщающиеся ссуды:
Наблюдение: На столе стоит наполненный прозрачный чайник. Что нужно сделать, чтобы налить чай в чашку?
Видно, что чайник и носик – сосуды, соединённые между собой отверстием в нижней части, поэтому жидкость заполняет их и находится на одном уровне, а верхнее отверстие носика расположено выше уровня жидкости в полном чайнике. Если чайник наклонить в сторону носика, то его отверстие опустится ниже уровня жидкости, и она будет вытекать из чайника в чашку.
Опыт. Возьмём две стеклянные трубки, соединим их резиновой трубкой, которую перекроем зажимом, и нальём в одну из трубок воды (рис. 105, а). Когда зажим снимем, то увидим, что жидкость в трубках установилась на одном уровне (рис. 105, б). Поднимем одну из трубок уровень жидкости в трубках не изменится (рис. 105, в).
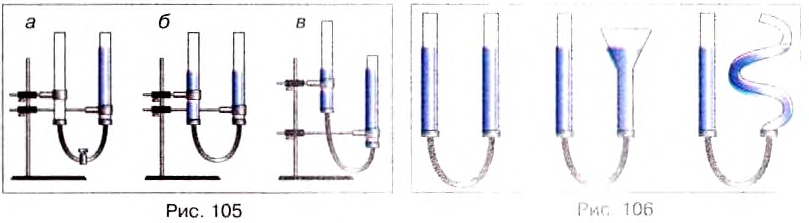
Соединённые между собой сосуды, в которых жидкость может свободно перетекать из одного сосуда в другой, называют сообщающимися сосудами.
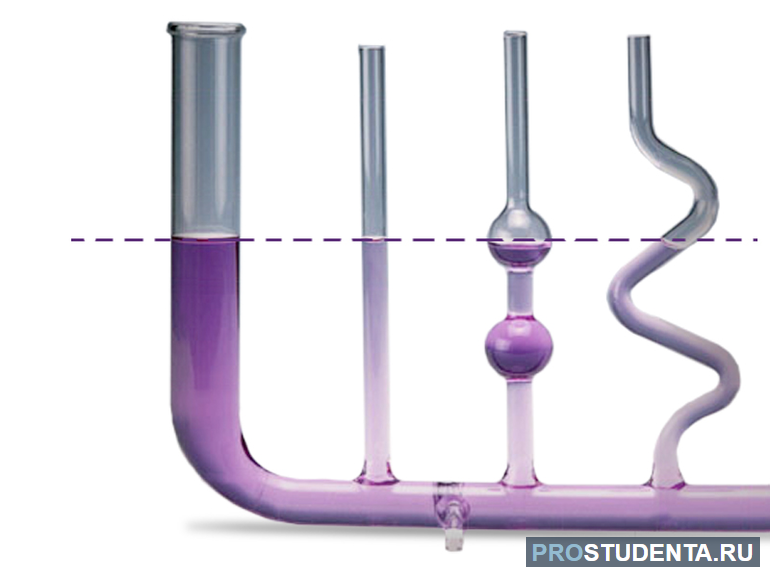
Заменим одну из трубок сообщающихся сосудов трубками другого диаметра и другой формы (рис. 106). В результате опыта убедимся, что свободные поверхности неподвижной однородной жидкости в сообщающихся сосудах любой формы находятся на одинаковом уровне. Отсюда вытекает закон сообщающихся сосудов.
В сообщающихся сосудах свободные поверхности однородной жидкости устанавливаются на одном уровне.
Для объяснения этого закона рассмотрим малые объемы жидкости в области поперечного сечения внизу соединительной трубки. В состоянии равновесия эти объемы находятся в покое, что означает равенство сил давления, действующих на них справа и слева от сечения. Поскольку площадь сечения одна и та же для левого и правого столбов жидкости, то и создаваемые ими гидростатические давления должны быть одинаковыми, а вместе с ними, по закону Паскаля, — и высоты обоих столбов, т. е. 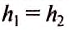
Если в один из сообщающихся сосудов налить, например, воду плотностью 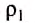 , а в другой — керосин плотностью
, а в другой — керосин плотностью 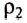 , то свободные поверхности этих жидкостей установятся на разных уровнях, причём уровень керосина будет выше, чем уровень воды (рис. 107).
, то свободные поверхности этих жидкостей установятся на разных уровнях, причём уровень керосина будет выше, чем уровень воды (рис. 107).
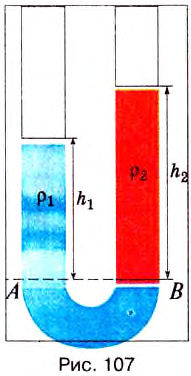
Поскольку жидкости в равновесии находятся в покое, то согласно закону Паскаля можно утверждать, что давления, создаваемые левым и правым столбами жидкости, например, на уровне раздела жидкостей АВ, одинаковы, т. е. 
Отсюда с помощью формулы гидростатического давления получим
соотношение: 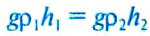
или после сокращения на 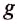 :
: 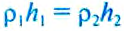
Из этого равенства следует пропорция: 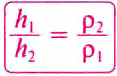
Видим, что высоты разнородных жидкостей, отсчитываемые от уровня поверхности их раздела, в сообщающихся сосудах обратно пропорциональны их плотностям. Для установления равновесия высота столба менее плотной жидкости должна быть большей.
Примеры сообщающихся сосудов: лейка для полива растений (рис. 108);

водомерное стекло парового котла – для определения уровня воды в котле; водяной уровень — для проведения горизонтальной линии на неровной местности. На основе закона сообщающихся сосудов действуют артезианские колодцы или скважины (рис. 109).

Скважину делают в наиболее низком месте водяного пласта, и вода поднимаясь на поверхность, бьёт фонтаном. Водонапорная сеть представляет собой разветвлённую сеть сообщающихся сосудов. Чтобы вода поступала в наивысшее место водонапорной сети, нужно водонапорную башню размещать не ниже этого места. Рассмотрим, как действует водопровод (рис. 110).
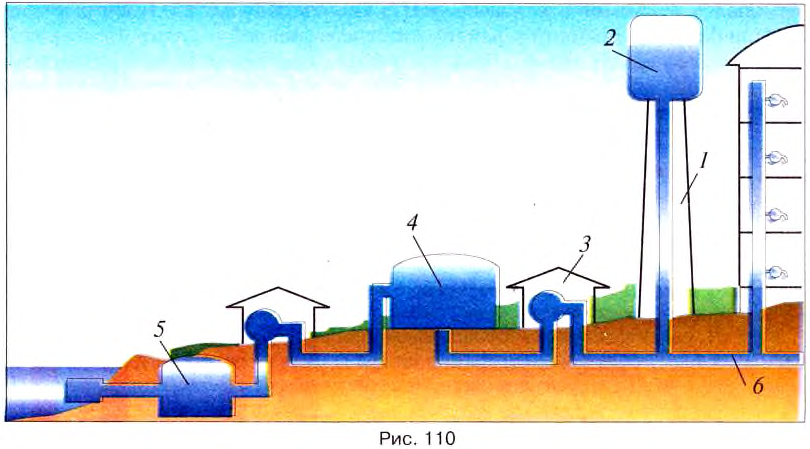
На водонапорной башне 1 установлен большой бак 2 для воды. С помощью мощных насосов 3 из водоёма (реки, озера) или скважины воду закачивают для очистки в отстойник 5, потом подают для фильтрования в резервуар 4, а дальше — в магистраль и в водонапорную башню. К магистрали 6 присоединены водопроводные трубы отдельных зданий. Чтобы вода в них зимой не замерзала, их изолируют и укладывают под землю. В каждом доме в квартирах на трубах устанавливают водяные краны. Когда открывают кран, вода начинает выливаться, так как уровень жидкости в башне выше, чем в квартире.
Примером сообщающихся сосудов являются шлюзы.
Шлюзы (от латинского шлеузе – удерживаю, отделяю) – это гидротехническое сооружение для перевода судов на реке или канале с одного уровня на другой.
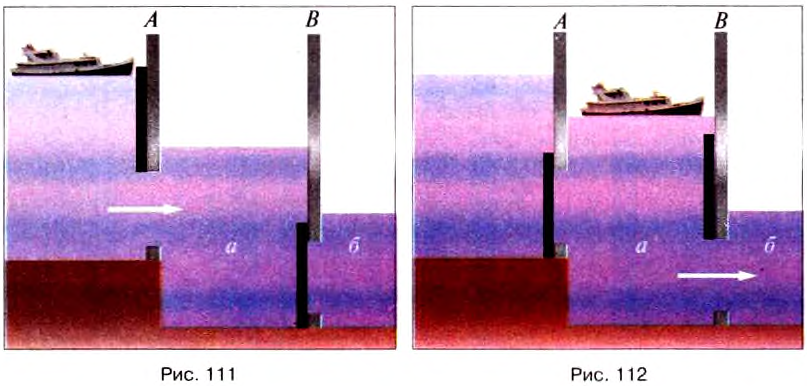
Шлюзы являются одним из ярких примеров применения сообщающихся сосудов в технике. Любой шлюз состоит из шлюзовой камеры, в которой есть верхние и нижние ворота. Камера соединена с рекой или каналом широкими трубами, которые закрывают выдвижными заслонками. На рисунках 111 — 112 показана схема действия шлюза, когда корабль плывёт по течению реки.
Когда корабль подходит к шлюзу, ворота А шлюза закрыты (рис. 111). Открывают заслонку трубы, соединяющей верхнюю часть реки с камерой. Вода из реки постепенно перетекает в камеру а. Когда уровень воды в камере а сравняется с её уровнем в верхней части реки, верхние ворота А открывают, и корабль входит в камеру а. После этого верхние ворота закрывают (рис. 112) и открывают заслонку трубы, соединяющей камеру а с нижней частью реки б. Камера шлюза а постепенно освобождается от воды до уровня её в нижней части реки б. Затем открывают нижние ворота В, и корабль выходит в реку.
При большой разности верхнего и нижнего уровней реки строят несколько шлюзовых камер, которые работают последовательно. Если будете плыть на теплоходе по Днепру из Киева в Чёрное море, то обязательно увидите такие шлюзы.
Сообщающиеся сосуды
Два или больше сосуда, соединенные трубками и заполненные жидкостью, называют сообщающимися сосудами.
Что происходит в сообщающихся сосудах
Возьмем два цилиндрических стеклянных сосуда, соединенных между собой трубкой (рис. 97). В один из них (справа) поместим очень легкий поршень, который плотно прилегает к стенкам и может свободно перемещаться в трубке вверх и вниз.
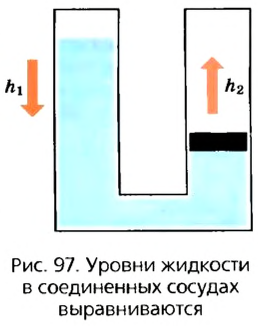
Придержим поршень и начнем наливать воду в левый сосуд до тех пор, пока высота столба в нем не будет равна высоте 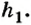 Под поршнем высота столба равна
Под поршнем высота столба равна 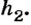 Причем
Причем 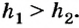
Если освободить поршень, то вследствие разности давлений поршень начнет подниматься вверх до тех пор, пока уровень жидкости в обоих сосудах не станет одинаковым. Это возможно тогда, когда высоты столбов жидкости в обоих сосудах будут одинаковыми:
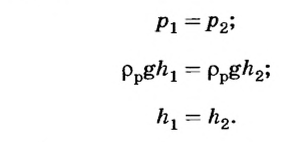
В сообщающихся сосудах однородная жидкость устанавливается на одном уровне.
Очевидно, что так будет тогда, если в обоих сосудах будет находиться однородная жидкость.
Что происходит в сообщающихся сосудах с различными жидкостями
Если в сосудах будут различные жидкости и 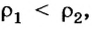 то
то 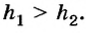 Но всегда
Но всегда

или

Применение сообщающихся сосудов
Свойства сообщающихся сосудов повсеместно используют в быту, технике, на производстве.
Всем известный чайник с носиком является сообщающимися 100 сосудами. Кончик носика расположен таким образом, что он находится на уровне крышки чайника. Поэтому залитая в чайник вода не выливается, когда сосуд стоит на горизонтальной поверхности (рис. 98).

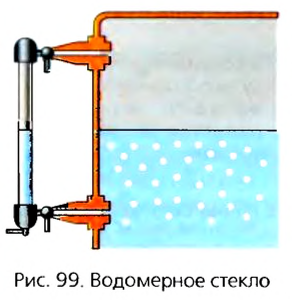
Контролируют уровень воды в паровых котлах при ее нагревании при помощи водомерного стекла (рис. 99). Это стеклянная трубка, нижний конец которой расположен ниже уровня воды в котле. А верхний конец соединен с пространством котла над уровнем воды. По показателям водоизмерительного стекла можно узнать об уровне воды в котле, не открывая его.
В небольших поселках действуют системы водопроводов, построенные по принципу сообщающихся сосудов (рис. 100). Обязательным элементом этой системы является так называемая водонапорная башня – металлический или бетонный резервуар, поднятый на такую высоту, чтобы уровень воды в нем был выше строений, в которые подается вода. Водяной насос наполняет резервуар водой, а с башни вода сама трубами поступает к потребителям соответственно закону сообщающихся сосудов.

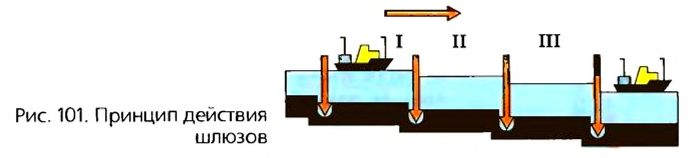
По принципу сообщающихся сосудов работают шлюзы (рис. 101), с помощью которых суда преодолевают различные препятствия на реках: пороги, плотины, мели и пр. Шлюзы – это система камер с водонепроницаемыми воротами. Если судно идет вниз по течению, то оно заходит в верхнюю камеру, ворота которой после этого закрываются. Вода из камеры выпускается в нижнюю камеру до тех пор, пока ее уровень не сравняется с уровнем воды в нижней камере. После этого открываются другие ворота, судно выходит из камеры и свободно плывет дальше по реке. Подобным способом суда поднимаются вверх против течения. Но в этом случае камера наполняется водой до тех пор, пока она не достигнет верхнего уровня воды в реке. Такие шлюзы, как правило, строят на судоходных реках, на которых построены водонапорные плотины.
- Заказать решение задач по физике
Сообщающиеся сосуды и манометры
Каждое утро мы умываемся. А знаете ли вы, почему течет вода из крана, когда мы его открываем? А почему выливается вода из носика чайника, если чайник наклонить? А как «работает» артезианский колодец? Может, кто-то из вас уже знает, что все эти устройства являются сообщающимися сосудами.
Сообщающиеся сосуды — это сосуды, которые соединены между собой так, что между ними может перетекать жидкость. Простейшие сообщающиеся сосуды — это две соединенные между собой трубки. Если в одну из трубок наливать воду, то вода будет перетекать в другую трубку. Когда движение воды прекратится, вода в обеих трубках (обоих коленах сообщающихся сосудов) установится на одном уровне (рис. 26.1, а). Если наклонить или поднять одно из колен, то вода будет перетекать из колена, расположенного выше, пока уровни воды в обоих коленах не сравняются (рис. 26.1, б). Итак, мы определили основное свойство сообщающихся сосудов: В открытых сообщающихся сосудах свободные поверхности однородной неподвижной жидкости располагаются на одном уровне. Обратите внимание! Свободные поверхности жидкости устанавливаются на одном уровне не только в двух, но и в любом количестве сообщающихся сосудов — независимо от того, какую форму они имеют и как расположены в пространстве (рис. 26.2). А вот если в правое и левое колена сообщающихся сосудов налить жидкости, которые не смешиваются и имеют разные плотности, например керосин и воду, результат будет иным. Рассмотрим рис. 26.3. На уровне CD давление столбов жидкостей в сосудах одинаково:
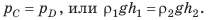
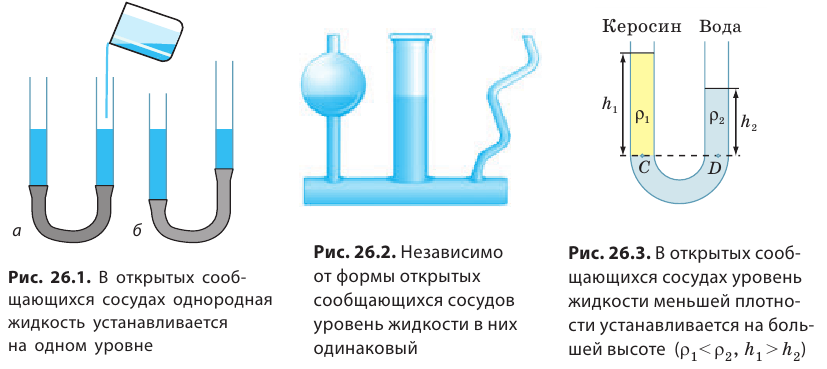
После сокращения на g получаем: 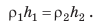 Следовательно, если
Следовательно, если 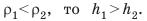 . Отсюда имеем еще одно свойство сообщающихся сосудов: В открытых сообщающихся сосудах столб неподвижной жидкости, имеющей меньшую плотность, будет выше, чем столб неподвижной жидкости, имеющей большую плотность. для двух открытых сообщающихся сосудов соотношение высот столбов жидкостей и плотностей этих жидкостей имеет вид:
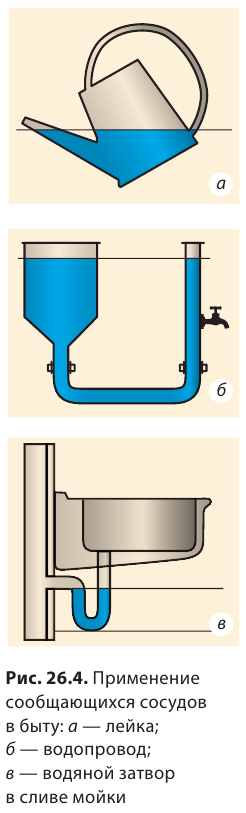
. Отсюда имеем еще одно свойство сообщающихся сосудов: В открытых сообщающихся сосудах столб неподвижной жидкости, имеющей меньшую плотность, будет выше, чем столб неподвижной жидкости, имеющей большую плотность. для двух открытых сообщающихся сосудов соотношение высот столбов жидкостей и плотностей этих жидкостей имеет вид: 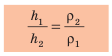 Сообщающиеся сосуды широко применяют в быту, медицине, технике, строительстве. Шлюзы на каналах и реках, водопроводы, водомерные трубки на паровых котлах, артезианские колодцы, фонтаны, чайники, воронки, капельницы — все это примеры сообщающихся сосудов. Рассмотрите рис. 26.4 и попробуйте объяснить принцип действия некоторых устройств.
Сообщающиеся сосуды широко применяют в быту, медицине, технике, строительстве. Шлюзы на каналах и реках, водопроводы, водомерные трубки на паровых котлах, артезианские колодцы, фонтаны, чайники, воронки, капельницы — все это примеры сообщающихся сосудов. Рассмотрите рис. 26.4 и попробуйте объяснить принцип действия некоторых устройств.
Изготовление открытого жидкостного манометра
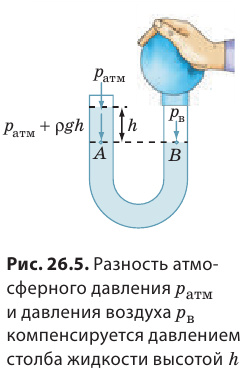
На правое колено U-образной трубки, в которую налита однородная жидкость, наденем резиновую грушу. Слегка сожмем грушу — жидкость в трубке установится таким образом, что высота столба жидкости в правом колене будет меньше, чем в левом, на h (рис. 26.5). Определим давление воздуха pв в правом колене трубки. На уровне АВ давление в жидкости одинаково 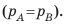 . В точке В это будет давление
. В точке В это будет давление 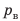 — давление воздуха в груше, в точке А — атмосферное давление
— давление воздуха в груше, в точке А — атмосферное давление 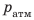 плюс гидростатическое давление столба жидкости высотой h. Получаем:
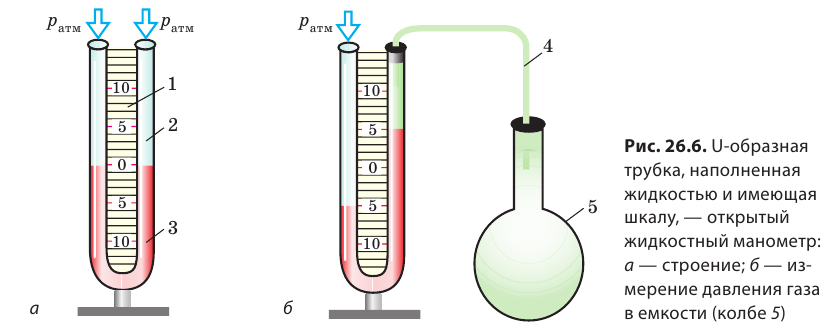
плюс гидростатическое давление столба жидкости высотой h. Получаем: 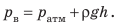 Итак, с помощью U-образной трубки, заполненной однородной жидкостью (известной плотности r), и линейки, позволяющей измерить разность уровней жидкости в коленах трубки (h), можно определить, на сколько давление газа в груше отличается от атмосферного. Соответствующий прибор называют открытый жидкостный манометр (рис. 26.6).
Итак, с помощью U-образной трубки, заполненной однородной жидкостью (известной плотности r), и линейки, позволяющей измерить разность уровней жидкости в коленах трубки (h), можно определить, на сколько давление газа в груше отличается от атмосферного. Соответствующий прибор называют открытый жидкостный манометр (рис. 26.6).
Манометр — это прибор для измерения давления жидкостей и газов. Открытый жидкостный манометр (рис. 26.6, а) состоит из линейки 1, к которой присоединена Uобразная трубка 2. Трубка заполнена подкрашенной жидкостью 3 так, что уровень жидкости расположен на отметке 0. При измерениях (рис. 26.6, б) одно колено трубки оставляют открытым в атмосферу, а второе с помощью шланга 4 соединяют с емкостью, в которой нужно измерить давление газа (колба 5). Например, на рис. 26.6, б разность уровней подкрашенной жидкости в сообщающихся сосудах составляет 10 см (h = 0,1 м). Если в трубке находится подкрашенная вода, то давление газа в колбе 5 меньше атмосферного давления на 980 Па:
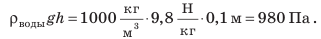
Заменяем жидкостный манометр металлическим:
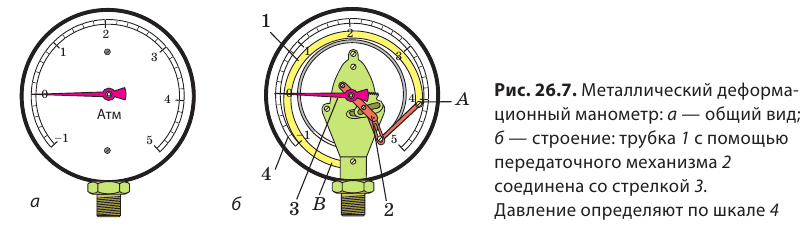
Жидкостный манометр не всегда удобен в использовании: необходимо доливать жидкость до нужного уровня, осуществлять дополнительные вычисления. Поэтому, как правило, используют металлические деформационные манометры (рис. 26.7). Основной элемент металлического деформационного манометра — гибкая дугообразная трубка 1, один конец которой (А) запаян. Второй конец трубки (В) соединен с резервуаром, в котором нужно измерить давление.
Принцип действия таких манометров следующий. Если давление газа внутри трубки больше атмосферного, то гибкая трубка распрямляется и ее движение передается через механизм 2 к стрелке 3, движущейся вдоль шкалы 4 прибора. После уменьшения давления газа до атмосферного трубка возвращается в начальное (недеформированное) положение, а стрелка останавливается на отметке 0. Шкала металлического манометра проградуирована в атмосферах или паскалях. Обратите внимание! Металлический деформационный манометр показывает, на сколько измеренное давление больше или меньше атмосферного.
Пример решения задачи
В правое колено открытой U-образной трубки, содержащей воду, налили слой керосина высотой 12,5 см (см. рисунок). Определите разность уровней воды и керосина в коленах трубки. Керосин и вода не смешиваются.
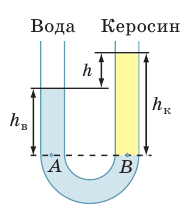
Анализ физической проблемы. В однородной жидкости давление на одном горизонтальном уровне одинаково. В обоих коленах на уровне AB и ниже находится вода, значит, на уровне AB давления, создаваемые атмосферой и жидкостями, одинаковы. Чтобы определить гидростатические давления жидкостей, нужно знать их плотности. Плотности воды и керосина узнаем из таблицы плотностей (с. 249). Задачу будем решать в единицах СИ.
Дано:
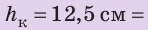
 ,
,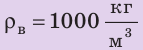 ,
,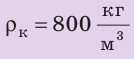
Найти:

Решение:
Разность высот столбов керосина и воды: 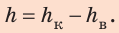 Определим высоту столба воды. Найдем давление в точках А и В:
Определим высоту столба воды. Найдем давление в точках А и В:
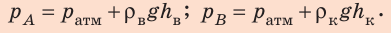
Поскольку 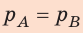 , то имеем:
, то имеем:
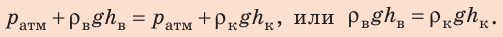
Отсюда найдем высоту столба воды:
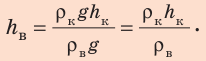
Проверим единицу, найдем значение высоты столба воды:
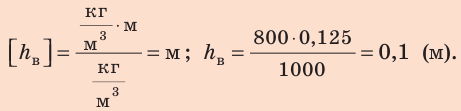
Таким образом, разность уровней воды и керосина в правом и левом коленах трубки: 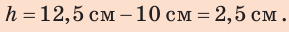
Ответ: h=2,5 см.
Итоги:
Сообщающиеся сосуды — это сосуды, которые соединены между собой так, что между ними может перетекать жидкость. В открытых сообщающихся сосудах разных форм и размеров свободная поверхность однородной неподвижной жидкости располагается на одном уровне; если плотности жидкостей в сосудах различны, то столб жидкости, имеющей меньшую плотность, выше, чем столб жидкости, имеющей большую плотность.
Манометры — это приборы для измерения давления жидкостей и газов. В открытом жидкостном манометре давление газа 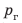 в сосуде определяется по разности h уровней жидкости в коленах прибора: если
в сосуде определяется по разности h уровней жидкости в коленах прибора: если 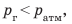 то
то 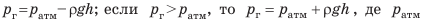 — атмосферное давление. На практике широко используют металлические деформационные манометры.
— атмосферное давление. На практике широко используют металлические деформационные манометры.
- Атмосферное давление в физике и его измерение
- Манометры в физике
- Барометры в физике
- Жидкостные насосы в физике
- Давление газов и жидкостей
- Движение жидкостей и газов
- Гидравлические машины в физике
- Весовое давление жидкостей в физике
Сообщающиеся сосуды, теория и онлайн калькуляторы
Сообщающиеся сосуды
Определение сообщающихся сосудов
Определение
Соединенные между собой сосуды называют сообщающимися.
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
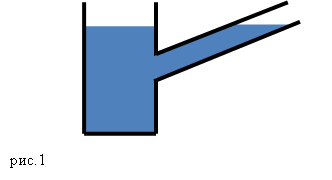
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
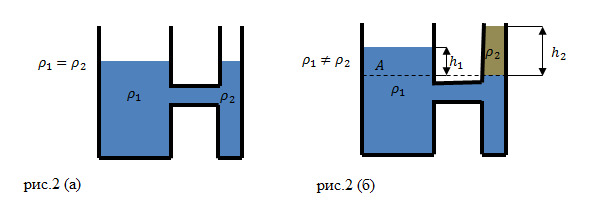
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
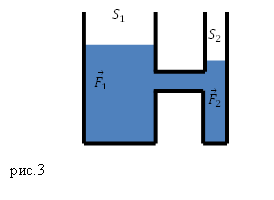
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
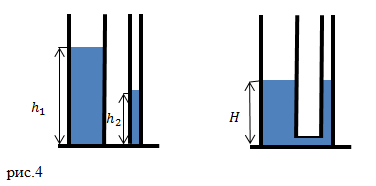
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Сообщающиеся сосуды. Гидравлический пресс
- Закон сообщающихся сосудов
- Сообщающиеся сосуды с различными жидкостями
- Гидравлический пресс
- Задачи
п.1. Закон сообщающихся сосудов
Как было показано в §31 данного справочника, давление столба жидкости не зависит от формы или размера дна сосуда. На одном и том же уровне (h) давление будет одинаковым.
Поэтому, когда жидкость приходит в равновесие, давление выравнивается, и её поверхность становится горизонтальной.
Второй случай с U-образной трубкой представляет значительный практический интерес, поскольку её колена являются так называемыми сообщающимися сосудами.
Сообщающиеся сосуды – сосуды с общим дном, в которых жидкость может свободно перетекать из одного колена в другое.
 |
Из сказанного выше следует, что при любой форме сообщающихся сосудов жидкость, налитая в них, будет перетекать, пока не установится на одном уровне в каждом из колен. |
Закон сообщающихся сосудов
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне.
п.2. Сообщающиеся сосуды с различными жидкостями
Теперь рассмотрим, какой уровень установится, если в U-образную трубку налить две несмешивающиеся жидкости с различной плотностью, например, керосин и воду.
 |
На рисунке пунктиром обозначен горизонтальный уровень, который проходит под слоем керосина. На этом уровне в обоих коленах трубки находится вода, а значит, давления по закону Паскаля одинаковы. Можем записать $$ rho_2gh_2=rho_1gh_1 Rightarrow frac{h_2}{h_1}=frac{rho_1}{rho_2} $$ Получаем
|
В сообщающихся сосудах с различными жидкостями уровень жидкости выше в сосуде, в котором находится жидкость с меньшей плотностью.
п.3. Гидравлический пресс
Закон Паскаля и закон сообщающихся сосудов позволяет создавать гидравлические механизмы с многократным выигрышем в силе.
Гидравлический пресс состоит из двух сообщающихся цилиндрических сосудов разного диаметра. Сосуды заполняются водой, маслом или другой жидкостью. По закону Паскаля давление одинаково по всем направлениям и передается по всему объему.

Если подействовать на меньший поршень слева силой (F_1), направленной вниз, под поршнем возникнет избыточное давление (p=frac{F_1}{S_1}). Это давление будет передаваться по всему объему в жидкости, и под большим поршнем справа получим (p=frac{F_2}{S_2}). На большой поршень будет действовать сила (F_2=pS_2=F_1frac{S_2}{S_1}), направленная вверх.
За счет разности площади поршней получаем выигрыш в силе $$ k=frac{F_2}{F_1}=frac{S_2}{S_1} $$
Отношение силы давления большого поршня к силе давления малого поршня равно отношению площади большого поршня к площади малого поршня.
Гидравлический пресс был изобретен в 1795 году и с тех пор нашёл множество применений в различных отраслях производства. В современных прессах можно получить силу порядка сотен миллионов ньютонов, что используется для штамповки изделий из металла, прессования картона и хлопка, выдавливания масла из семян и т.д.
п.4. Задачи
Задача 1. Диаметр одного цилиндрического ведра в 1,2 раза больше, чем другого. В оба ведра налили по 5 л воды. В каком ведре давление на дно больше и во сколько раз?
Дано:
(d_1=1,2=d_2)
(V=5 text{л})
__________________
(frac{p_2}{p_1}-?)
Площадь дна каждого из ведер $$ S_1=frac{pi d^2_1}{4}, S_2=frac{pi d^2_2}{4} $$ Найдем высоту столба воды в каждом из ведер $$ V=ShRightarrow h_1=frac{V}{S_1}=frac{4V}{pi d^2_1}, h_2=frac{4V}{pi d^2_2} $$ Давление на дно в каждом из ведер $$ p_1rho gh_1=rho gcdotfrac{4V}{pi d^2_1}, p_2rho gh_2=rho gcdotfrac{4V}{pi d^2_2} $$ Отношение давлений $$ frac{p_2}{p_1}=frac{rho gcdot frac{4V}{pi d^2_2}}{rho gcdot frac{4V}{pi d^2_1}}=frac{d^2_1}{d^2_2}=left(frac{d_1}{d_2}right)^2 $$ Давление больше в узком ведре.
Отношение давлений равно отношению квадратов диаметров. $$ frac{p_2}{p_1}=1,2^2=1,44 $$ Ответ: больше в узком ведре; в 1,44 раза
Задача 2. Горизонтально расположенная труба заполнена водой и имеет два поршня. Площади поршней (S_1=10 text{см}^2, S_2=1 text{дм}^2). На поршень (B) действует сила (10 text{кН}). С какой силой нужно действовать на поршень (A), чтобы уравновесить силу, действующую на поршень (B)?
Дано:
(S_1=10 text{см}^2=0,001 text{м}^2)
(S_2=1 text{дм}^2=0,01 text{м}^2)
(F_2=10 text{кН}=10^4 text{Н})
__________________
(F_1-?)
При действии силы (F_2) на поршень (B) в воде возникает давление $$ p=frac{F_2}{S_2}. $$ По закону Паскаля давление передается во все стороны, и у поршня (A) получаем $$ p=frac{F_1}{S_1}. $$ Для уравновешивающей силы $$ frac{F_1}{S_1}=frac{F_2}{S_2}Rightarrow F-1=F_2frac{S_1}{S_2} $$ Подставляем $$ F_1=10^4cdot frac{0,001}{0,01}=10^3 (text{Н})=1 (text{кН}) $$ Ответ: 1 кН
Задача 3. U-образную трубку частично заполнили водой. В левое колено долили слой керосина высотой 25 см. В каком колене установился уровень выше? Найдите перепад высот (h) между уровнями поверхности воды в правом колене и уровнем керосина в левом колене. Ответ запишите в сантиметрах.
Дано:
(h_2=25 text{см}=0,25 text{м})
(rho_1=1000 text{кг/м}^3)
(rho_2=800 text{кг/м}^3)
__________________
(h-?)
На уровне под слоем керосина в обоих коленах трубки находится вода, а значит, давления на этом уровне по закону Паскаля одинаковы в обоих коленах. Можем записать $$ rho_2gh_2=rho_1gh_1Rightarrow h_1=frac{rho_2}{rho_1}h_2 $$ Поскольку плотность керосина меньше, уровень в левом колене с керосином выше.
Разность уровней begin{gather*} h=h_2-h_1=h_2-frac{rho_2}{rho_1}h_2\[7pt] h=left(1-frac{rho_2}{rho_1}right)h_2 end{gather*} Получаем: $$ h=left(1-frac{800}{1000}right)cdot 0,25=0,05 (text{м})=5 (text{см}) $$ Ответ: в левом колене с керосином; 5 см
Задача 4*. На дно мензурки налита ртуть и в нее опущен конец стеклянной трубки, запаянной сверху. Поверх ртути в мензурку налили слой воды высотой 25 см.
На какую высоту поднимется ртуть в стеклянной трубке?
Примите для расчетов (p_text{атм}=1,013cdot 10^5 text{Па}, g=9,8 text{м/с}^2)
Ответ укажите в миллиметрах.
На какую высоту поднимется ртуть при тех же условиях, если трубка не запаяна сверху?
Дано:
(rho_1=1000 text{кг/м}^3)
(rho_2=13600 text{кг/м}^3)
(h_1=25 text{см}=0,25 text{м})
(gapprox 9,8 text{м/с}^2)
(p_text{атм}=1,013cdot 10^5 text{Па})
__________________
(h_2-?, h’_2-?)
Рассмотрим запаянную трубку. На поверхность ртути, в которую опущен конец трубки, оказывают давление столб воды и атмосфера: $$ p=p_1+p_text{атм}=rho_1gh_1+p_text{атм} $$ Под действием этого давления ртуть в запаянной трубке поднимется на высоту $$ h_2=frac{p}{rho_2g}=frac{rho_1gh_1+p_text{атм}}{rho_2g} $$ Получаем $$ h_2=frac{1000cdot 9,8cdot 0,25+1,013cdot 10^5}{13600cdot 9,8}approx 0,778 (text{м})=778 (text{мм}) $$ Если трубка будет не запаяна, то при подъеме в ней ртути на нее сверху будет действовать атмосферное давление. Высота подъема begin{gather*} h’_2=frac{p-p_text{атм}}{rho_2g}=frac{rho_1gh_1}{rho_2g}=frac{rho_1}{rho_2}h_1\[7pt] h’_2=frac{1000}{13600}cdot 0,25approx 0,018 (text{м})=18 (text{мм}) end{gather*} Ответ: 778 мм; 18 мм
Примечание: заметим, что разность (h_text{атм}=778-18 = 760 text{мм}) – это нормальное атмосферное давление, измеренное в «миллиметрах ртутного столба» (см. §31 данного справочника). Поэтому (h_2=h’_2+h_text{атм}).
Задача 5. Малый поршень гидравлического пресса под действием силы 500 Н опустился на 9 см. При этом большой поршень поднялся на 3 см.
Какая сила действует на большой поршень со стороны жидкости?
Дано:
(F_1=500 text{Н})
(h_1=9 text{см}=0,09 text{м})
(h_2=3 text{см}=0,03 text{м})
__________________
(F_2-?)
Объем воды, вытесняемый при движении малого поршня вниз: (V=h_1S_1).
Жидкости практически несжимаемы, поэтому этот объем должен «прирасти» в цилиндре большого поршня за счет его движения вверх: (V=h_2S_2).
Получаем для выигрыша в силе: $$ h_1S_1=h_2S_2Rightarrow frac{S_2}{S_1}=frac{h_1}{h_2} $$ Выигрыш в силе равен отношению длин хода малого и большого поршней.
Выигрывая в силе, мы проигрываем в расстоянии.
Сила, действующая на большой поршень: $$ F_2=F_1frac{S_2}{S_1}=F_1frac{h_1}{h_2} $$ Подставляем: $$ F_2=500cdot frac{0,09}{0,03}=1500 (text{Н})=1,5 (text{кН}) $$ Ответ: 1,5 кН
Задача 6. Малый поршень гидравлического пресса площадью 1 м2 под действием силы 2 кН опустился на 24 см. Площадь большего поршня 8 м2. Найдите вес груза, который был поднят большим поршнем и высоту, на которую он был поднят.
Дано:
(S_1=1 text{м}^2)
(F_1=2000 text{Н})
(h_1=24 text{см}=0,24 text{м})
(S_2=8 text{м}^2)
__________________
(P-?, h_2-?)
Вес груза, который можно поднять с помощью пресса, равен силе (F_2), которая действует на большой поршень: $$ P=F_2=F_1frac{S_2}{S_1} $$ Получаем $$ P=2000cdot frac 81=16000 (text{Н})=16 (text{кН}) $$ Объем воды, вытесняемый при движении малого поршня вниз: (V=h_1S_1).
Жидкости практически несжимаемы, поэтому этот объем должен «прирасти» в цилиндре большого поршня за счет его движения вверх: (V=h_2S_2).
Следовательно $$ h_1S_1=h_2S_2Rightarrow h_2=h_1frac{S_1}{S_2} $$ Получаем begin{gather*} h_2=0,24cdot frac 81=0,03 (text{м})=3 (text{см}) end{gather*} Ответ: 16 кН; 3 см
Задача 7*. На дне аквариума лежал камень массой 390 г, полностью погруженный в воду. Когда его убрали, давление воды на дно аквариума уменьшилось на 25 Па. Найдите плотность камня, если длина аквариума 40 см, а ширина 14 см. ((g=9,8 text{м/с}^2)).
Дано:
(m=390 text{г}=0,39 text{кг})
(Delta p=25 text{Па})
(a=40 text{см}=0,4 text{м})
(b=14 text{см}=0,14 text{м})
(rho_0=1000 text{кг/м}^3)
(g=9,8 text{м/с}^2)
__________________
(rho-?)
Лежа на дне, камень занимал в аквариуме некий объем $$ V_text{к}=frac{m}{rho} $$ Остальной объем занимала вода. Их суммарный объем $$ V=V_text{в}+V_text{к}=Sh=abh $$ Высота слоя воды в аквариуме с камнем $$ h_1=frac{V_text{в}+V_text{к}}{ab} $$ Давление воды на дно в аквариуме с камнем begin{gather*} p_1=rho_0gh_1= rho_0gfrac{V_text{в}+V_text{к}}{ab} end{gather*} Когда камень забрали, в аквариуме осталась только вода объемом (V_text{в}).
Высота слоя воды в аквариуме без камня $$ h_2=frac{V_text{в}}{ab} $$ Давление воды на дно в аквариуме без камня $$ p_2=rho_0gh_2=rho_0gfrac{V_text{в}}{ab} $$ Разность давлений $$ Delta p=p_1-p_2=rho_0 gfrac{V_text{в}+V_text{к}}{ab}-rho_0gfrac{V_text{в}}{ab}=rho_0gfrac{V_text{к}}{ab}=frac{rho_0g}{ab}cdot frac{m}{rho} $$ Откуда плотность камня $$ rho=frac{rho_0g}{ab}cdot frac{m}{Delta p} $$ Подставляем $$ rho=frac{1000cdot 9,8}{0,4cdot 0,14}cdotfrac{0,39}{25}=2730 (text{кг/м}^3) $$ Ответ: 2730 кг/м3
Задачи на Сообщающиеся сосуды
Теоретический материал, используемый для решения задачи на сообщающиеся сосуды смотрите в конспекте «Сообщающиеся сосуды. Гидравлический пресс. Шлюзы».
Сообщающиеся сосуды — два или более соединённых между собой сосудов (ниже уровни жидкости), в которых жидкость может свободно перетекать из одного сосуда в другой.
Закон сообщающихся сосудов: в открытых сообщающихся сосудах любой формы при равновесии давление жидкости на любом горизонтальном уровне одинаково.
Схематически это выглядит таким образом, что в точках А и В ⇒ рA = рB. 
ρ1gh1 + ρ2gh2 = ρ3gh3 + ρ4gh4
Обратите внимание! Ниже уровня, на котором находятся точки А и В, жидкость однородна. Обозначения: р — давление, ρ — плотность, h — высота, g — ускорение свободного падения (9,8 м/с^2).
Следствие 1: в открытых сообщающихся сосудах при равновесии высоты столбов жидкостей, отсчитываемые от уровня, ниже которого жидкость однородна, обратно пропорциональны плотностям этих жидкостей.
 Следствие 2: в открытых сообщающихся сосудах при равновесии однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов.
Следствие 2: в открытых сообщающихся сосудах при равновесии однородная жидкость всегда устанавливается на одинаковом уровне независимо от формы сосудов.
В гидравлическом прессе сообщающиеся сосуды разных сечений S2 и S1 заполненные однородной жидкостью, используют для получения выигрыша в силе — F2/F1, равного — S2/S1.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
В левом колене сообщающихся сосудов налита вода, в правом — керосин. Высота столба керосина 20 см. Рассчитайте, на сколько уровень воды в левом колене ниже верхнего уровня керосина.
Ответ: 0,04 м (или 4 см). 
Задача № 2.
В сообщающихся сосудах находятся ртуть и вода. Высота столба воды 68 см. Какой высоты столб керосина следует налить в левое колено, чтобы ртуть установилась на одинаковом уровне?
Ответ: 0,85 м (или 85 см). Чтобы увидеть решение задачи, нажмите на спойлер ниже.
Задача № 3.
Уровень жидкостей в сосудах одинаковый. В левом налита вода, в правом — керосин. Одинаковы ли давления на дно? Одинаковы ли давления на кран? Будет ли переливаться жидкость из одного сосуда в другой, если открыть кран?
ЗАДАЧИ на Сообщающиеся сосуды
Задача № 4.
В сообщающихся сосудах находятся ртуть, вода и керосин. Какова высота слоя керосина, если высота столба воды равна 20 см и уровень ртути в правом колене ниже, чем в левом, на 0,5 см?
Ответ: 0,335 м (или 33,5 см).
Смотреть РЕШЕНИЕ задачи

Задача № 5.
Площадь малого поршня гидравлического пресса равна 10 см2, большого — 50 см2. На малый поршень поместили гирю массой 1 кг. Какой груз нужно поместить на большой поршень, чтобы жидкость осталась в равновесии?
Ответ: 5 кг.
Смотреть РЕШЕНИЕ задачи

Задача № 6.
Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?
Ответ: 2,7 м.
Смотреть РЕШЕНИЕ задачи

Задача № 7.
В U-образный сосуд налито 3 жидкости: вода, мед и масло. Высота воды в левом колене 40 см, высота масла в правом колене 30 см. Найдите разницу высот столбов меда в левом и правом коленах. Ответ округлить до сотых.
Ответ: ≈ 0,09 м.
Задача № 8.
В цилиндрических сообщающихся сосудах находится ртуть. Площадь поперечного сечения широкого сосуда в пять раз больше площади поперечного сечения узкого сосуда. В узкий сосуд наливают воду, которая образует столб высотой 34 см. На сколько поднимется уровень ртути в широком сосуде и на сколько опустится в узком?
Ответ: в широком сосуде на 0,42 см, в узком — на 2,1 см.
Задача № 9.
Высота воды в левом колене сообщающихся сосудов h1 = 40 см, в правом h2 = 10 см. В каком направлении будет переливаться вода, если открыть кран? На сколько изменится уровень воды в левом сосуде? Найти объем воды, который перелился из одного сосуда в другой. Левое колено сосуда имеет площадь поперечного сечения S1 = 10 см2, правое S = 20 см2.
Ответ: в правый; 0,2 м; 0,2 л.
Смотреть РЕШЕНИЕ задачи

Задача № 10.
В два колена сообщающихся сосудов налили ртуть. После установления равновесия высота ртути оказалась равна 25 см. Затем в левый сосуд (левое колено) добавили воду. Высота столба воды оказалась равна 20 см. Определите уровень ртути в левом и правом колене после добавления воды. Плотность воды 1 г/см3. Плотность ртути 13600 кг/м3.
ОТВЕТ: в левом — 0,24265 м (≈24,3 см), в правом — 0,25735 м (≈25,7 см).
Вы смотрели: Конспект урока по физике «Задачи на Сообщающиеся сосуды и Гидравлический пресс». Выберите дальнейшие действия:
- Перейти к теме: Задачи на давление твердых тел с ответами и решениями.
- Перейти к теме: Задачи на давление жидкостей с ответами и решениями.
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике
Из-за перепадов высот реки имеют разные глубины, что затрудняет или даже делает невозможным движение по ним судов. Поэтому строят шлюзы, которые рассчитывают по принципу сообщающихся сосудов. Формулы, используемые для вычислений, были получены в результате теоретического анализа, а после подтверждены экспериментально. Эти правила применяют при строении фонтанов, гидравлических прессов, плотин и различных устройств.
Оглавление:
- Общие сведения
- Условие равновесия
- Опыт на сообщение
- Решение примеров
Общие сведения
В древние времена перед человечеством возникла проблема доставки воды в свои жилища. Так появились акведуки, а после и водопроводные трубы, канализация. В те времена механизмы ещё не были придуманы, поэтому задача решалась с помощью природных сил. Суть изобретений заключалась в организации самотёка жидкости за счёт изменения высот желобов и труб.
Использование таких систем хоть и позволяло справляться с поставленной задачей, но приносило определённые неудобства. Работа трубопроводов заключалась в использовании свойств жидкости перетекать из одного места в другое за счёт изменения оказываемого давления.
В 1684 году Паскаль продемонстрировал парадокс. Для этого он использовал:
- закрытую бочку с водой;
- герметичную трубку;
- кружку.

Его опыт заключался в следующем. Один конец трубки был вставлен в бочку, а второй вертикально поднят на высоту порядка шести метров. В свободный конец Паскаль вылил кружку воды. Из-за малого диаметра трубки вода стала подниматься, а бочка лопнула. Как оказалось, в середине ёмкости создалось большое давление, привёдшее к её повреждению.
Этот парадокс объясняется законом Архимеда. Он гласит, что на тело, погруженное в воду, действует выталкивающая сила, равная весу жидкости. Значит, тело не сможет плавать в ней. Но это ошибочное рассуждение. Так как на самом деле архимедова сила появляется из-за гидростатического давления, зависящего от размера водяного столба, а не веса воды.
Поэтому тело и может находиться на поверхности резервуара, если его масса будет меньше веса воды. Это возможно, когда резервуар ненамного превышает размеры физического тела. Например, судно не тонет в ограниченном доке, так же как в и открытом океане, несмотря на то что масса воды между плавающим средством и стенами порта может быть меньше, чем вес корабля.
Закон Паскаля описывается формулой давления: P = F / S, где:
- p — давление;
- F — приложенная сила;
- S — площадь поверхности сосуда.
Из выражения следует, что увеличение силы на стенки удерживающие возрастает пропорционально. Давление принято изменять в ньютонах на квадратный метр или в паскалях. Этот закон нашёл применение в тормозных системах, гидравлических прессах.
Условие равновесия
Пусть имеются два сосуда, при этом они могут иметь разную форму и размеры. В нижней части они сообщаются, то есть соединяются с помощью трубки, которая имеет запорный вентиль. Ёмкость, стоящую слева, удобно обозначить цифрой один, соответственно, с правой стороны — два. В первую колбу можно налить жидкость, высота столба которой составляет h1. Её плотность пусть будет равняться p1. Во втором сосуде налито другое вещество с плотностью p и расстоянием от поверхности до дна h2.
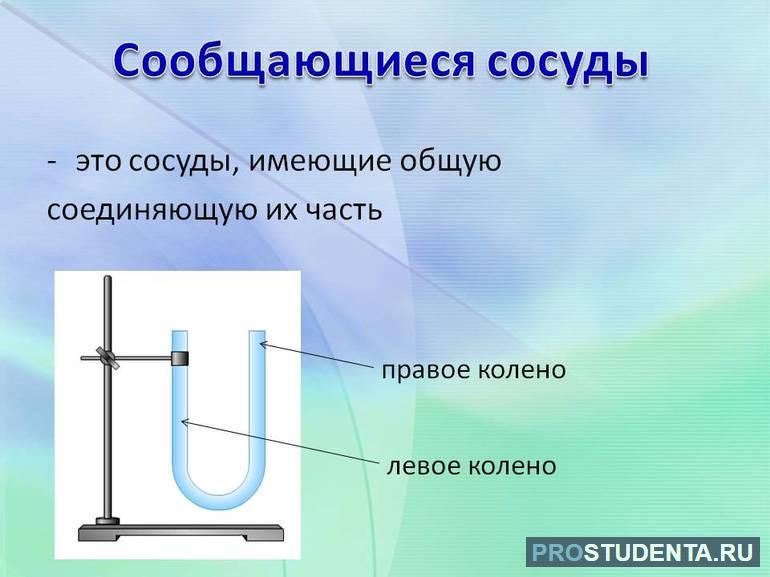
Можно предположить, что высоты столбов подобраны так, что при открытии крана движение водного раствора не произойдёт. То есть он не будет перетекать из одной ёмкости в другую. Это важно для рассуждений, так как в другом случае жидкости просто перемешаются. Поэтому пусть растворы находятся в состоянии равновесия. Значит, давление и в первом, и во втором сосудах в нижних точках трубки будет одинаковым.
Действительно, если представить, что вместо крана стоит лёгкая перегородка, то для того, чтобы она осталась на своём месте, давление с её двух сторон должно быть скомпенсировано. Другими словами, в системе должны действовать одинаковые силы.
Так как растворы находятся в равновесии, то можно записать: P1 = P2. Давление можно выразить через плотность и высоту столба. Для рассматриваемого случая оно будет гидростатическим. Определяют его по формуле: p = ρ * g * h, где:
- ρ — плотность искомой жидкости;
- g — ускорение свободного падения;
- h — высота столба.
Полученное равенство справедливо как для первой, так и второй ёмкости. Его можно подставить в равенство равновесия: ρ1 * g * h1 = ρ2 * g * h2. После того как левую и правую часть сократить на g, формула примет вид: ρ1 * h1 = ρ2 * h2. Последнее выражение для сообщающихся сосудов и описывает условие равновесия.

Теперь можно рассмотреть частный случай, когда обе ёмкости заполнены однородной жидкостью. Это означает, что ρ1 = ρ2 = ρ. Условие равновесия примет вид: ρh1 = ρh2. Выражение можно сократить на плотность. Отсюда следует, что h1 = h2. Найденное правило называют математическим действием закона сообщающихся сосудов.
Опираясь на выведенную формулу, можно сформулировать закон словами. Но для этого нужно вспомнить, что такое h1 и h2. По сути, это расстояние от свободной поверхности жидкости, рассчитываемое по вертикали. Отсюда следует определение, что свободные поверхности однородной жидкости в соединённых ёмкостях устанавливаются на одинаковой высоте.
Опыт на сообщение
Чтобы открыть свой закон, Паскалю понадобилось использовать для опытов только два сосуда. Всё дело в том, что, согласно формуле, на установившийся уровень жидкости не влияет форма, размер, масса и другие характеристики. Если они сообщающиеся, то высота столба во всех ёмкостях будет одинаковой.
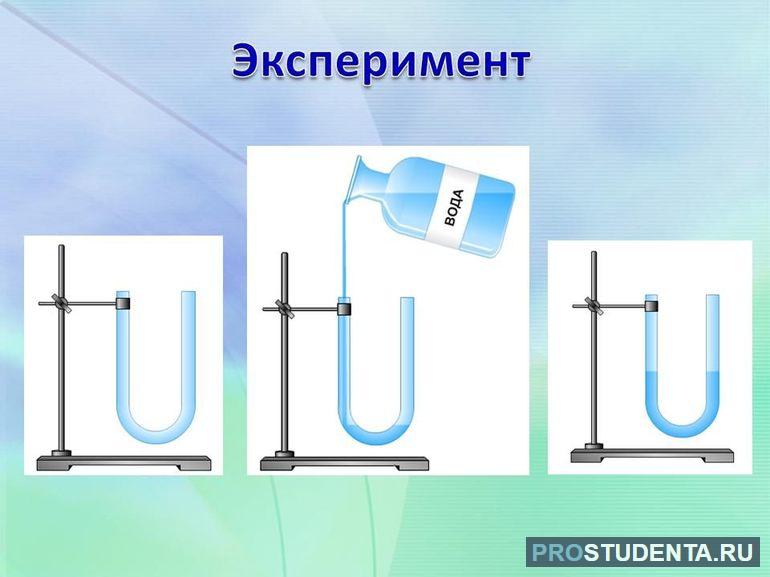
Для того чтобы самостоятельно убедиться в действии закона, можно провести простой эксперимент. Понадобится взять два любых шприца, наполнить один из них водой и соединить с другим трубочкой. Затем поднять их на любой уровень и убедиться, что водяная линия столбов будет находиться в одной горизонтали. Причём она не изменится даже при наклоне сосудов.
Проведённый опыт не будет называться полным, если не провести эксперимент с разными жидкостями. Так, если налить растворы с отличающейся плотностью, то можно наблюдать, что водяной столб не сможет выровняться.
Например, такое явление особо заметно, если попробовать смешать раствор поваренной соли и воды. Интересно то, что высота столба будет настолько меньше, насколько отличается плотность.
Решение примеров
В школе после рассмотрения темы преподаватель часто предлагает школьникам написать реферат или подготовить небольшое сообщение для видеоурока. В таком докладе, кроме теории, рекомендуется приводить несколько задач. Их решение желательно сопровождать рисунками, чтобы наглядно продемонстрировать в проекте, как работают сообщающиеся сосуды.
Физики обычно демонстрируют полезность явления на следующих двух примерах:

- Труба с площадью сечения S погружена в чашу со ртутью на одну треть. Не изменяя положение нижнего конца трубки, её наклон изменили на угол j. Определить, как поменялась высота. Если принять размер столба ртути за h, то, зная площадь сечения трубки, можно вычислить объём жидкости: V = S * h. Длину, которую занимает жидкость, можно определить так: l = h / cos (j). Значит, объём будет равняться: V1 = S * l = (S * h) / cos (j). Отсюда возможно определить изменение объёма в трубке: ΔV = V1 — V = (S * h) / c o s (j) — S * h. Так как площадь ёмкости равняется: S = π * D2 / 4, то искомая высота составит: Δh = Δ V * S = 4 * S * h * (1 − cos (j) / cos (j) * π * D 2 ).
- Какой площадью нужно изготовить отливной поршень в водяном прессе, чтобы выигрыш был в шесть раз? Площадь большого рычага равна двум метрам. Рассматриваемая система есть не что иное, как гидравлический пресс. То есть это два сообщающихся сосуда. Если принять, что большему поршню S соответствует сил F, а меньшему — S1 и F1, то по закону Паскаля они будут относиться друг к другу как F / S = F1 / S1. Из этого равенства можно выразить искомую площадь: S1 = F1 * S / F. Согласно условию: F1 / F = 6. Значит, расчётная формула примет вид: S = S * n = 2 * 6 = 12.
Даже не заглядывая в Википедию, можно привести множество примеров использования свойства как в быту, так и в природе. Например, перелив в ванной, поилка для домашних птиц, различные устройства полива, чайник, фонтаны, шлюзы. В работе всех этих вещей используется закон для сообщающихся сосудов. Но самый простой пример — это применяемый в строительстве водяной уровень. Причём его конструкция настолько проста, что повторить её сможет любой даже в домашних условиях.
