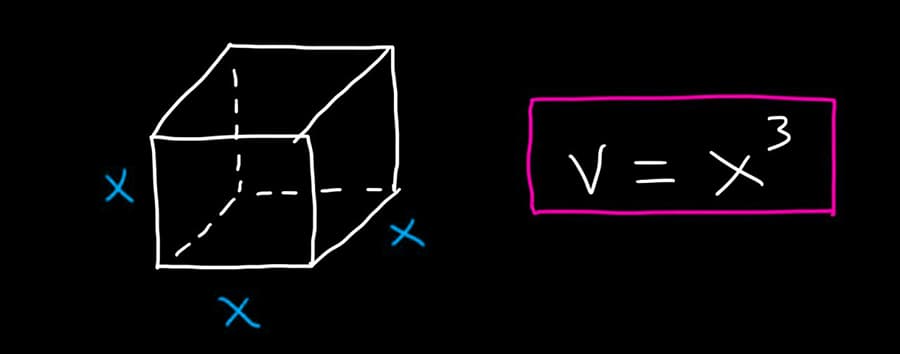Калькулятор объема куба
Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
Что известно
Длина
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🧊 Что считает калькулятор
Калькулятор объема куба — это инструмент, который позволяет вычислять объем любого куба и выводить результат в разных единицах измерения.
Куб – правильный многогранник, каждая грань которого представляет собой квадрат. Все ребра куба равны. Куб является частным случаем параллелепипеда и призмы.
Как использовать калькулятор
Укажите значение стороны куба, после этого калькулятор произведет расчёт и выдаст его в указанных единицах измерения. Кроме того, можно указать диагональ куба или диагональ любой его стороны.
Что влияет на точность расчетов калькулятора
Точность расчетов калькулятора объема куба зависит от нескольких факторов:
- Корректность ввода данных. Если вводимые значения длины, ширины и высоты куба некорректны, то расчет объема будет неправильным. Поэтому, важно убедиться в правильности вводимых значений перед выполнением расчета.
- Точность математических операций. Расчет объема куба требует выполнения математических операций, таких как умножение. Если калькулятор не выполняет математические операции точно, то результаты расчетов будут неточными.
- Точность округления. В некоторых случаях, результаты расчетов могут быть округлены. Если калькулятор округляет результаты до неправильного числа знаков, то результаты будут неточными.
- Алгоритм расчета. Различные калькуляторы могут использовать разные алгоритмы расчета. Если алгоритм расчета неправильный, то результаты могут быть неточными.
- Ошибки программирования. Если в программе калькулятора есть ошибки, то результаты расчетов могут быть неправильными. Поэтому, важно использовать калькуляторы, которые были разработаны и протестированы надежными разработчиками.
Где можно применить калькулятор
Калькулятор объема куба может быть использован во многих областях, где требуется расчет объема кубической формы. Некоторые из таких областей включают:
- 🧱 Строительство. Калькулятор объема куба может использоваться строителями при расчете объема кубических блоков, бетонных кубов, кирпичей и других материалов, используемых в строительстве.
- 🏭 Производство. Калькулятор объема куба может использоваться в производственных процессах для расчета объема материалов, таких как металл, пластик, стекло и другие, используемые в производстве кубических изделий.
- 📦 Логистика. Калькулятор объема куба может использоваться при планировании грузоперевозок, чтобы определить, сколько грузовых мест может вместить транспортное средство.
- 🎓 Образование. Калькулятор объема куба может использоваться учителями математики в школах и университетах для обучения геометрии и расчета объема кубических форм.
- 🎨 Интерьер и дизайн. Калькулятор объема куба может использоваться в дизайне интерьера для расчета объема кубических элементов, таких как шкафы, полки, столы и другие.
- 🛠️ Ремонт и обслуживание. Калькулятор объема куба может использоваться в ремонте и обслуживании, чтобы определить количество материалов, необходимых для замены кубических элементов, таких как плитка, обои и другие.
📐 Как посчитать объем куба
Объем куба можно вычислить самостоятельно, используя формулу
V = a³
где V – объем куба, a – длина ребра.
Для того, чтобы вычислить объем куба, нужно измерить длину одного из его ребер с помощью линейки или другого инструмента измерения длины. После этого возведите полученное значение в куб, используя калькулятор или ручной расчет.
Например, если длина ребра куба равна 5 см, то объем куба будет равен V = 5³ = 125 кубических сантиметров.
Важно помнить, что все единицы измерения должны быть одинаковыми – если длина ребра измеряется в сантиметрах, то и объем будет выражен в кубических сантиметрах.
🤔 Полезные советы
Несколько советов, которые могут помочь при вычислении объема куба:
- Определите длину одной из сторон куба. Обычно все стороны куба одинаковые, поэтому вы можете выбрать любую.
- Возведите длину стороны куба в квадрат. Это даст вам площадь одной грани куба.
- Умножьте площадь одной грани куба на 6. Это даст вам общую площадь поверхности куба.
- Определите длину любой из диагоналей куба. Вы можете использовать формулу теоремы Пифагора для нахождения длины диагонали, если известна длина стороны.
- Возвести длину диагонали куба в куб. Это даст вам объем куба.
- Если известна масса куба, можно использовать плотность материала для расчета его объема. Для этого нужно разделить массу на плотность.
- Убедитесь, что вы используете одни и те же единицы измерения при расчете. Например, если длина стороны куба измеряется в сантиметрах, то и объем должен быть выражен в кубических сантиметрах.
❓ Вопросы и ответы
Сейчас мы предлагаем вам посмотреть ответы на вопросы, которые часто задаются на данную тему.
Что такое объем куба и как его рассчитать?
Объем куба — это мера его вместимости, то есть объем пространства, которое он занимает. Он рассчитывается по формуле V = a³, где a – длина ребра куба.
Как найти длину ребра куба, если известен его объем?
Для этого нужно извлечь кубический корень из объема: a = V^(1/3). Это позволит определить длину ребра куба, зная его объем.
Что произойдет с объемом куба, если увеличить длину его ребра вдвое?
Объем куба увеличится в 8 раз. Это происходит потому, что объем куба пропорционален кубу его длины: V ~ a³. Если длина ребра увеличивается вдвое, то объем увеличивается в 222=8 раз.
Какие единицы измерения используются для объема куба?
Объем куба измеряется в кубических единицах длины, таких как кубические метры (м³), кубические сантиметры (см³), кубические дюймы (дюйм³) и т.д.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
- Калькулятор площади трапеции. Рассчитайте онлайн площадь трапеции, не только зная длины ее оснований и высоту, но и по другим известным параметрам, например, диагоналям.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
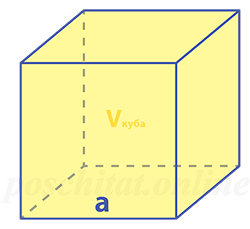
Формула объёма куба через ребро
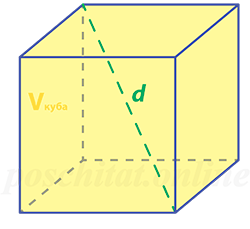
Формула объёма куба через диагональ грани
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d – диагональ грани куба
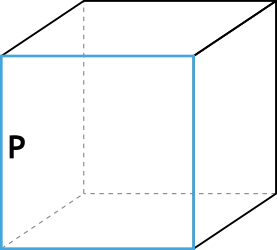
Формула объёма куба через периметр грани
{V= Big( dfrac{P}{4} Big) ^3}
P – периметр грани куба
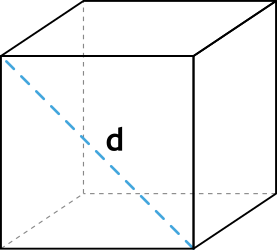
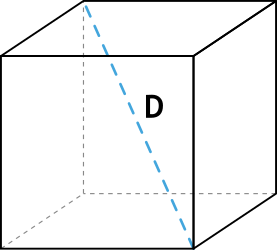
Формула объёма куба через диагональ куба
{V= dfrac{D^3}{3sqrt{3}}}
D – диагональ куба
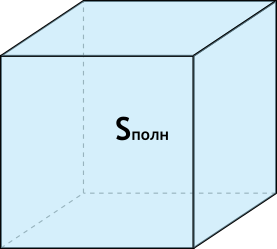
Формула объёма куба через площадь полной поверхности
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн – диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
-
Примеры задач
Формула вычисления объема куба
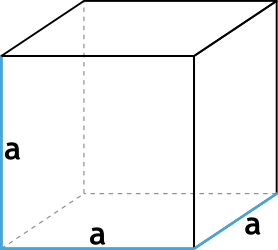
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3
2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.
Следовательно, вычислить объем куба можно так:
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
Объём куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём куба
Чтобы найти объём куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Объём куба через ребро
Чему равен объём куба, если:
ребро a =
Vкуба =
0
Округление ответа:
Объём куба через диагональ
Чему равен объём куба, если:
диагональ d =
Vкуба =
0
Округление ответа:
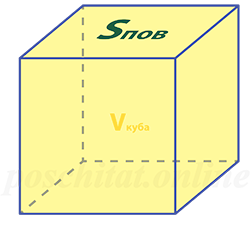
Объём куба через площадь поверхности
Чему равен объём куба, если:
Sпов =
Vкуба =
0
Округление ответа:
Теория
Как найти объём куба зная длину ребра
Чему равен объём куба Vкуба, если длина его рёбер a:
Формула
Vкуба = a³
Пример
Для примера, найдём объём куба, у которого рёбра a = 5 см:
Vкуба = 5³ = 125 см³
Как найти объём куба зная диагональ
Чему равен объём куба Vкуба, если его диагональ d:
Формула
Vкуба = d³ ⁄3√3
Пример
Для примера, найдём объём куба, длина диагонали которого d = 9 см:
Vкуба = 9³ / 3√3 ≈ 729 / 5,2 ≈ 140 см³
Как найти объём куба зная площадь поверхности
Чему равен объём куба Vкуба, если площадь поверхности этого куба Sпов:
Формула
Vкуба = √Sпов³ ⁄6√6
Пример
Для примера, найдём объём куба, площадь поверхности которого Sпов = 24 см²:
Vкуба = √24³ / 6√6 = 24√24 / 6√6 = 4√4 = 8 см³
См. также
Как посчитать объём в емкостях различных форм?
Содержание
- Объем шара
- Объем куба
- Объем пирамиды
- Объем параллелепипеда
- Объем правильного тетраэдра
- Объем конуса
- Объем призмы
- Как высчитать объем бочки в литрах?
- Как найти объем бочки по диаметру?
- Как узнать объём прямоугольной тары
- Как определить объём сферического изделия
- Как вычислить объём цистерны выполненной в виде цилиндра
- Как рассчитать объем цилиндра с помощью калькулятора
- Внутренний объем погонного метра трубы в литрах — таблица
- Расчет объема воды, находящейся во всей системе
- Способы перевода кубометров в другие кубические единицы
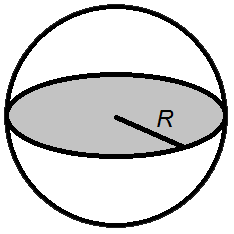
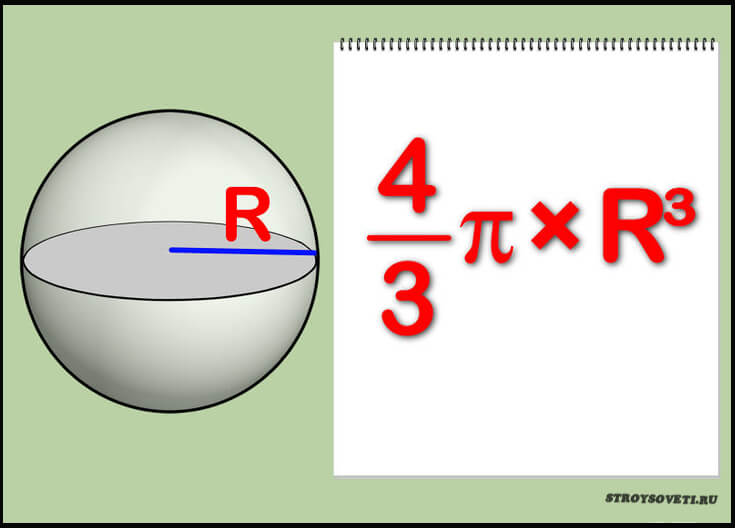
1 Объем шара
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V — объем шара,
R — радиус шара,
π = 3.141592
к меню ↑
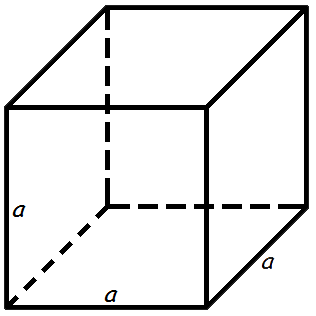
2 Объем куба
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3где V — объем куба,
a — длина грани куба
к меню ↑
3 Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды
к меню ↑
4 Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · hгде V – объем параллелепипеда,
So – площадь основания,
h – длина высоты
к меню ↑
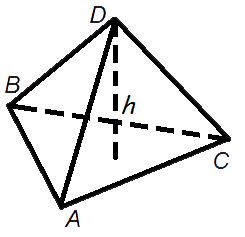
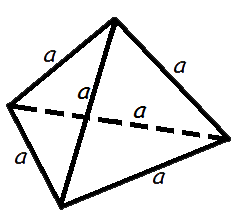
5 Объем правильного тетраэдра
Формула объема правильного тетраэдра:
где V – объем правильного тетраэдра,
a – длина ребра правильного тетраэдра
к меню ↑
6 Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
где V – объем конуса,
So – площадь основания конуса,
R – радиус основания конуса,
h – высота конуса,
π = 3.141592.
к меню ↑
7 Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So hгде V – объем призмы,
So – площадь основания призмы,
h – высота призмы
к меню ↑
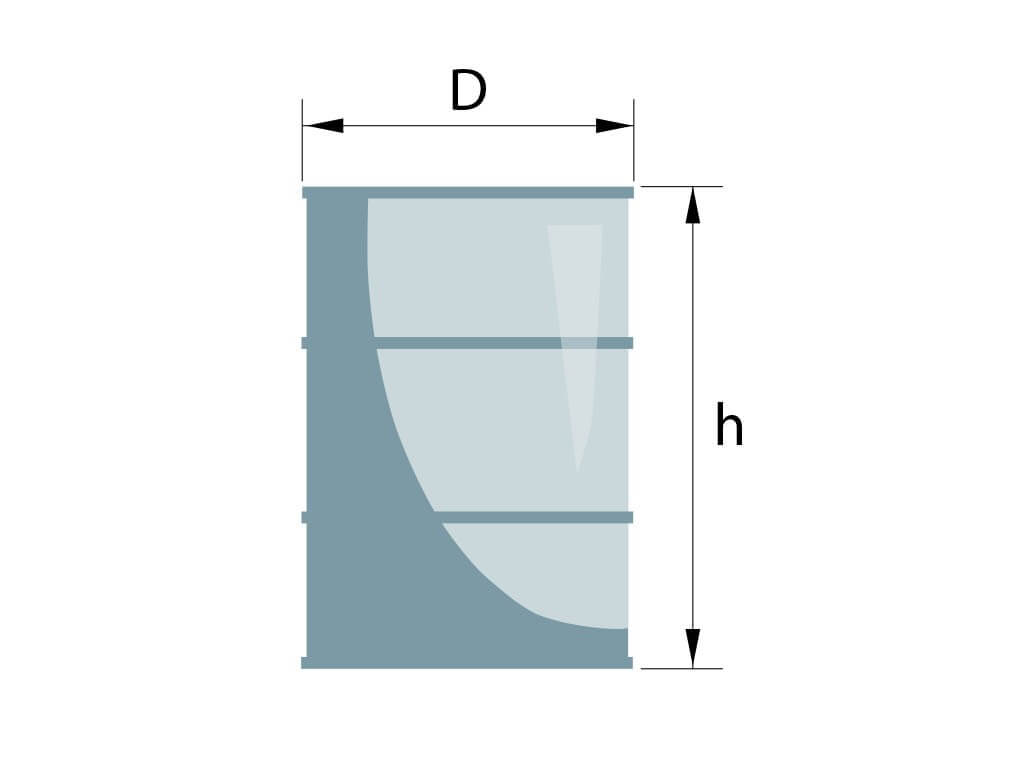
8 Как высчитать объем бочки в литрах?
Теперь, когда мы знаем объем бочки в м.куб, можно перевести это значение в литры, а для этого использую соотношение: 1 куб. метр = 1000 литров.
Тогда, объем бочки в литрах будет равен:
0.31 м3 * 1000 литров = 310 литров
к меню ↑
9 Как найти объем бочки по диаметру?
Для того, чтобы найти объем бочки по диаметру необходимо преобразовать стандартную формулу, по которой обычно находят объем цилиндра через радиус и высоту:
V = Пи * r² * h
Зная, что диаметр равен двум радиусам, получаем следующую формулу, которую можно применить для нахождения объема бочки в м3, по диаметру и высоте:
V = Пи * d²/4 * h
Все расчеты необходимо проводить в единой мере измерения длины, в нашем случае — это метры.
Для примера, необходимо найти объем цилиндрической бочки зная диаметр и высоту:
- D = 84 см — диаметр бочки;
- h = 56 см — высота бочки.
Подставляем данные в формулу, предварительно переведя см в метры:
V бочки в м3 = 3,14159 * (0,84 м)² / 4 * 0,56 м = 0,3103 м3
Если округлить, то получается, что объем цилиндрической бочки с размерами D = 84 см, h = 56 см = 0,31 м3
к меню ↑
10 Как узнать объём прямоугольной тары
В сфере строительства все показатели объёма приведены к конкретным величинам. Расчёты могут проводиться в литрах или дм 3 , но чаще всего для определения количества того или иного материала используются кубические метры. Как рассчитать кубатуру самых простых прямоугольных ёмкостей опишем дальше на конкретном примере.
Для работы нам понадобится тара, строительная рулетка и блокнот с ручкой или карандашом для проведения вычислений. Из курса геометрии известно, что объём подобных тел вычисляется умножением длины, ширины и высоты изделия. Формула расчётов сводится к следующему
V=a*b*c, где a, b и с – стороны тары.
Например, длина нашего изделия равняется 150 сантиметрам, ширина 80 сантиметрам, высота 50 сантиметров. Для правильного подсчёта кубатуры указанные величины переводим в метры и проводим необходимые расчёты V=1,5*0,8*0,5=0,6м3.
к меню ↑
11 Как определить объём сферического изделия
Сферические изделия встречаются в нашей жизни почти каждый день. Это может быть элемент подшипника, футбольный мяч или пишущая часть шариковой ручки. В некоторых случаях нам необходимо узнать, как рассчитать кубатуру сферы для определения количества жидкости в ней.
Как утверждают эксперты, для вычисления объёма этой фигуры используется формула V=4/3ԉr3, где:
- V – подсчитываемый объём детали;
- R- радиус сферы;
- ԉ – постоянная величина, которая равняется 3,14.
Для проведения необходимых вычислений нам нужно взять рулетку, зафиксировать начало измерительной шкалы и провести замер, причём лента рулетки должна проходить по экваторe шара. После этого узнают диаметр детали, поделив размер на число ԉ.
А теперь ознакомимся с конкретным примером вычисления для сферы, если её длина по окружности равняется 2,5 метрам. Сначала определим диаметр 2,5/3,14=0,8 метра. Теперь подставляем это значение в формулу:
к меню ↑
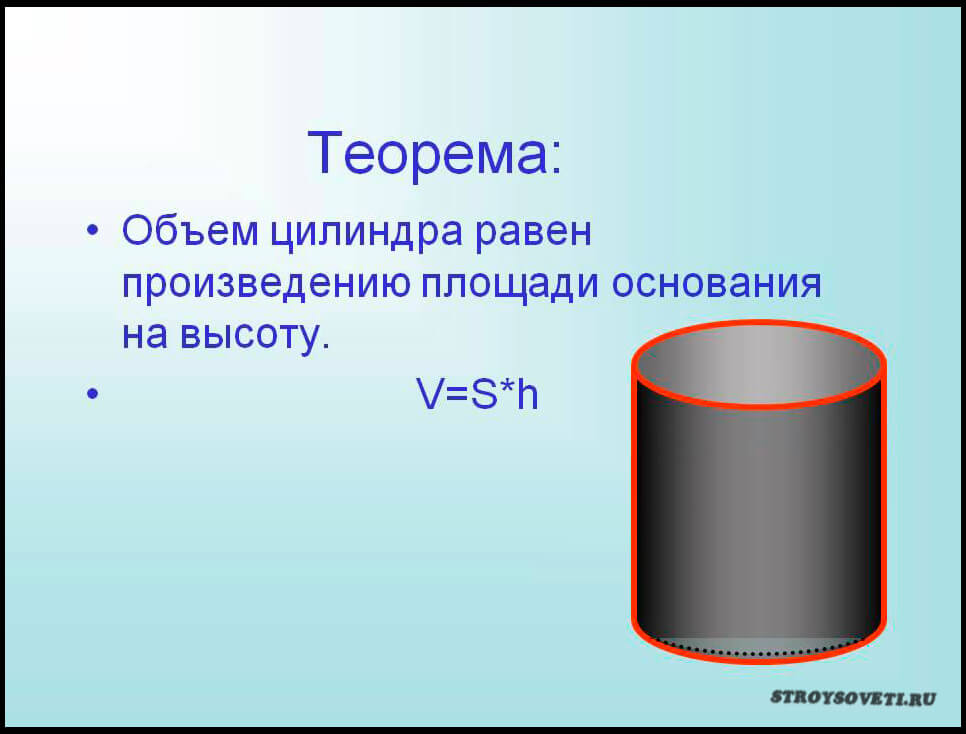
12 Как вычислить объём цистерны выполненной в виде цилиндра
Подобные геометрические фигуры используются для хранения пищевых продуктов, транспортирования топлива и других целей. Многие не знают, как рассчитать объем воды, но основные нюансы такого процесса опишем дальше в нашей статье.
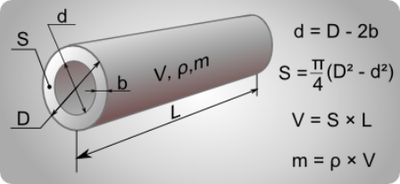
Высоту жидкости в цилиндрической ёмкости определяют по специальному устройству метрштоку. В данном случае емкость цистерны вычисляется по специальным таблицам. Изделия со специальными таблицами измерения объёма в жизни встречаются редко, поэтому подойдём к решению проблемы другим путём и опишем, как рассчитать объём цилиндра по специальной формуле – V=S*L, где
- V- объём геометрического тела;
- S – площадь сечения изделия в конкретных единицах измерения (м³);
- L – длина цистерны.
Показатель L можно измерить при помощи всё той же рулетки, но площадь сечения цилиндра придётся считать. Показатель S вычисляют по формуле S=3,14*d*d/4, где d – диаметр окружности цилиндра.
А теперь ознакомимся с конкретным примером. Допустим, длина нашей цистерны имеет значение 5 метров, её диаметр 2,8 метра. Сначала вычислим площадь сечения геометрической фигуры S= 3,14*2,8*2,8/4=6,15м. А теперь можно приступать к вычислению объёма цистерны 6,15*5= 30,75 м³.
к меню ↑
12.1 Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
- площадь основания и высота цилиндра;
- радиус основания и высота цилиндра;
- диаметр основания и высота цилиндра.
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
к меню ↑
13 Внутренний объем погонного метра трубы в литрах — таблица
Таблица показывает внутренний объем погонного метра трубы в литрах. То есть сколько потребуется воды, антифриза или другой жидкости (теплоносителя), чтобы заполнить трубопровод. Взят внутренний диаметр труб от 4 до 1000 мм.
Внутренний диаметр,ммВнутренний объем 1 м погонного трубы, литровВнутренний объем 10 м погонных трубы, литров
| 4 | 0.0126 | 0.1257 |
| 5 | 0.0196 | 0.1963 |
| 6 | 0.0283 | 0.2827 |
| 7 | 0.0385 | 0.3848 |
| 8 | 0.0503 | 0.5027 |
| 9 | 0.0636 | 0.6362 |
| 10 | 0.0785 | 0.7854 |
| 11 | 0.095 | 0.9503 |
| 12 | 0.1131 | 1.131 |
| 13 | 0.1327 | 1.3273 |
| 14 | 0.1539 | 1.5394 |
| 15 | 0.1767 | 1.7671 |
| 16 | 0.2011 | 2.0106 |
| 17 | 0.227 | 2.2698 |
| 18 | 0.2545 | 2.5447 |
| 19 | 0.2835 | 2.8353 |
| 20 | 0.3142 | 3.1416 |
| 21 | 0.3464 | 3.4636 |
| 22 | 0.3801 | 3.8013 |
| 23 | 0.4155 | 4.1548 |
| 24 | 0.4524 | 4.5239 |
| 26 | 0.5309 | 5.3093 |
| 28 | 0.6158 | 6.1575 |
| 30 | 0.7069 | 7.0686 |
| 32 | 0.8042 | 8.0425 |
| 34 | 0.9079 | 9.0792 |
| 36 | 1.0179 | 10.1788 |
| 38 | 1.1341 | 11.3411 |
| 40 | 1.2566 | 12.5664 |
| 42 | 1.3854 | 13.8544 |
| 44 | 1.5205 | 15.2053 |
| 46 | 1.6619 | 16.619 |
| 48 | 1.8096 | 18.0956 |
| 50 | 1.9635 | 19.635 |
| 52 | 2.1237 | 21.2372 |
| 54 | 2.2902 | 22.9022 |
| 56 | 2.463 | 24.6301 |
| 58 | 2.6421 | 26.4208 |
| 60 | 2.8274 | 28.2743 |
| 62 | 3.0191 | 30.1907 |
| 64 | 3.217 | 32.1699 |
| 66 | 3.4212 | 34.2119 |
| 68 | 3.6317 | 36.3168 |
| 70 | 3.8485 | 38.4845 |
| 72 | 4.0715 | 40.715 |
| 74 | 4.3008 | 43.0084 |
| 76 | 4.5365 | 45.3646 |
| 78 | 4.7784 | 47.7836 |
| 80 | 5.0265 | 50.2655 |
| 82 | 5.281 | 52.8102 |
| 84 | 5.5418 | 55.4177 |
| 86 | 5.8088 | 58.088 |
| 88 | 6.0821 | 60.8212 |
| 90 | 6.3617 | 63.6173 |
| 92 | 6.6476 | 66.4761 |
| 94 | 6.9398 | 69.3978 |
| 96 | 7.2382 | 72.3823 |
| 98 | 7.543 | 75.4296 |
| 100 | 7.854 | 78.5398 |
| 105 | 8.659 | 86.5901 |
| 110 | 9.5033 | 95.0332 |
| 115 | 10.3869 | 103.8689 |
| 120 | 11.3097 | 113.0973 |
| 125 | 12.2718 | 122.7185 |
| 130 | 13.2732 | 132.7323 |
| 135 | 14.3139 | 143.1388 |
| 140 | 15.3938 | 153.938 |
| 145 | 16.513 | 165.13 |
| 150 | 17.6715 | 176.7146 |
| 160 | 20.1062 | 201.0619 |
| 170 | 22.698 | 226.9801 |
| 180 | 25.4469 | 254.469 |
| 190 | 28.3529 | 283.5287 |
| 200 | 31.4159 | 314.1593 |
| 210 | 34.6361 | 346.3606 |
| 220 | 38.0133 | 380.1327 |
| 230 | 41.5476 | 415.4756 |
| 240 | 45.2389 | 452.3893 |
| 250 | 49.0874 | 490.8739 |
| 260 | 53.0929 | 530.9292 |
| 270 | 57.2555 | 572.5553 |
| 280 | 61.5752 | 615.7522 |
| 290 | 66.052 | 660.5199 |
| 300 | 70.6858 | 706.8583 |
| 320 | 80.4248 | 804.2477 |
| 340 | 90.792 | 907.9203 |
| 360 | 101.7876 | 1017.876 |
| 380 | 113.4115 | 1134.1149 |
| 400 | 125.6637 | 1256.6371 |
| 420 | 138.5442 | 1385.4424 |
| 440 | 152.0531 | 1520.5308 |
| 460 | 166.1903 | 1661.9025 |
| 480 | 180.9557 | 1809.5574 |
| 500 | 196.3495 | 1963.4954 |
| 520 | 212.3717 | 2123.7166 |
| 540 | 229.0221 | 2290.221 |
| 560 | 246.3009 | 2463.0086 |
| 580 | 264.2079 | 2642.0794 |
| 600 | 282.7433 | 2827.4334 |
| 620 | 301.9071 | 3019.0705 |
| 640 | 321.6991 | 3216.9909 |
| 660 | 342.1194 | 3421.1944 |
| 680 | 363.1681 | 3631.6811 |
| 700 | 384.8451 | 3848.451 |
| 720 | 407.1504 | 4071.5041 |
| 740 | 430.084 | 4300.8403 |
| 760 | 453.646 | 4536.4598 |
| 780 | 477.8362 | 4778.3624 |
| 800 | 502.6548 | 5026.5482 |
| 820 | 528.1017 | 5281.0173 |
| 840 | 554.1769 | 5541.7694 |
| 860 | 580.8805 | 5808.8048 |
| 880 | 608.2123 | 6082.1234 |
| 900 | 636.1725 | 6361.7251 |
| 920 | 664.761 | 6647.6101 |
| 940 | 693.9778 | 6939.7782 |
| 960 | 723.8229 | 7238.2295 |
| 980 | 754.2964 | 7542.964 |
| 1000 | 785.3982 | 7853.9816 |
Если у вас специфическая конструкция или труба, то в формуле выше показано как вычислить точные данные для правильного расхода воды или иного теплоносителя.
к меню ↑
13.1 Расчет объема воды, находящейся во всей системе
Для определения такого параметра, необходимо в формулу подставить значение внутреннего радиуса. Однако сразу появляется проблема. А как рассчитать полный объем воды в трубе всей отопительной системы, в которую входят:
- Радиаторы;
- Расширительный бачок;
- Котел отопления.
Сначала рассчитывается объём радиатора. Для этого открывается его технический паспорт и выписывается значения объема одной секции. Этот параметр умножается на число секций в конкретной батарее. Например, одна секция чугунного радиатора равен 1,5 литрам.
Когда установлен биметаллический радиатор, это значение намного меньше. Количество воды в котле можно узнать из паспорта устройства.
Для определения объема расширительного бака, его заполняют измеренным заранее, количеством жидкости.
Очень просто определяется объём труб. Имеющиеся данные для одного метра, определенного диаметра, нужно просто умножить на длину всего трубопровода.
Заметим что в глобальной сети и справочной литературе, можно увидеть специальные таблицы. Они показывают ориентировочные данные изделия. Погрешность приведенных данных достаточно мала, поэтому приведенные в таблице значения, можно смело использовать для вычисления объема воды.
Надо сказать, что при расчете значений, нужно учитывать некоторые характерные отличия. Металлические трубы, имеющие большой диаметр, пропускают количество воды, значительно меньше, чем такие же полипропиленовые трубы.
Причина кроется в гладкости поверхности труб. У стальных изделий она выполнена с большой шероховатостью. ППР трубы не имеют шероховатости на внутренних стенках. Однако при этом стальные изделия имеют больший объем воды, чем в других трубах, одинакового сечения. Поэтому чтобы убедиться, что расчет объема воды в трубах произведен верно, нужно несколько раз перепроверить все данные и подкрепить результат онлайн-калькулятором.
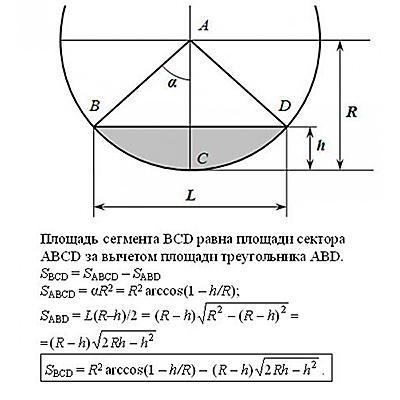
Формула определения площади сечения неполностью заполненных труб:
к меню ↑
14 Способы перевода кубометров в другие кубические единицы
Рассчитывая объемности, необходимо придерживаться одинаковых единиц замеров. Если данные представлены другими единицами, а конечный результат должен быть получен в кубах, то достаточно будет правильно сделать преобразование.
Если V измерен в мм3, см3, дм3, л, то в м3 переводим соответственно:
- 1 м3 = 1 мм3 х х 0, 000000001 = 1 мм3 х 10-9;
- 1 м3 = 1 см3 х 0, 000001 = 1 см3 х 10-6;
- 1 м3 = 1 дм3 х 0,001 = 1 дм3 х 10-3. Такой же перевод применяют и для литров, поскольку в 1 л содержится 1 дм3.
Чтобы найти кубы вещества, зная его массу, нужно по таблице отыскать его плотность или определить вручную. Разделив заданную массу М (кг) на показатель плотности Р (кг/ м3), получим V материала (м3).
Подсчитать кубические метры не составляет трудностей для человека, не имеющего математических наклонностей, несмотря на то что в каждом случае требуется разный подход.
Знания для определения объемов необходимы и специалистам, и обычным людям в повседневной жизни.
Источники
- https://ru.onlinemschool.com/math/formula/volume/
- https://exceltut.ru/formuly-obema-geometricheskih-figur-najti-vse-obemy/
- https://zametkiddach.ru/obem-bochki-kalkulyator
- https://iobogrev.ru/rasschitat-obem-baka-v-litrah-po-razmeram
- https://StroySoveti.ru/kanalizaciya/kak-rasschitat-obem-emkosti-razlichnoy-formyi.html
- https://VseProTruby.ru/vodoprovodnye/raschet-obema-vody-v-trube.html
- http://LediZnaet.ru/deti/mir-znanij/kak-poschitat-obyom.html
[свернуть]
‘;