Как найти объем стенок полого шара - Сайт, где вы сможете решить свои вопросы

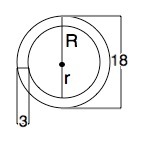
Объём стенок шара равен разности между объёмом шара с внешним диаметром и объёмом шара с внутренним диаметром.
R– радиус внешней сферы равен D:2=9 см
r – радиус внутренней сферы равен 9-3=6 см
Формула объёма шара
$V= frac } \ V_ = frac =972 pi \ V_ = frac =288 pi \$
V стенки=972π-288π=684π см³

Источник

Масса полой детали

Никогда не устану повторять, что масса тела — это его объем , умноженный на плотность его материала rho (см. таблицы плотностей):

Однако, в случае полой или пустотелой детали мы будем иметь дело не с объемом ее тела, а с объемом ее стенок. Объем стенок полой детали проще всего представить как разность объемов двух сплошных тел: с внешними размерами и с внутренними (из полного объема тела вычитается объем внутренней пустоты).
Формулы для объема сплошных тел можно найти в статье «Масса сплошной детали».

Примечание. В приведенных ниже формулах все размеры измеряются в миллиметрах, а плотность — в граммах на кубический сантиметр.
Буквой обозначено отношение длины окружности к ее диаметру, составляющее примерно 3,14.

1. Масса трубки (полого цилиндра)

Объем стенок трубки: $V~=~{pi{D^2/4}L}~-~{pi{(D~-~2T)^2/4}L}$ , где — внешний диаметр трубки, — длина трубки, — толщина стенки.
После упрощения получаем формулу для объема:
Тогда масса трубки:

2. Масса полого (пустотелого) шара

шар Объем стенок шара: $V~=~{pi/6}*(D^3~-~(D~-~2T)^3)$ , где — внешний диаметр шара, — толщина стенки.
Тогда масса:

$m~=~pi~*~{{D^3~-~(D~-~2T)^3}/6000}~*~rho$

3. Масса полого сегмента шара

Объем стенок сегмента шара: $V={pi/6}H((H^2+{3/4}D^2)~-~((H-T)^2+{3/4}(D-2T)^2))$ , где — внешний диаметр основания сегмента, — высота сегмента, — толщина стенки*.
После упрощения получаем формулу для объема:
Тогда масса:

4. Масса полого усеченного конуса

Объем стенок круглого усеченного конуса: $V={pi/12}H(D1^2+D1*D2+D2^2-(D1-2T)^2-(D1-2T)(D2-2T)-(D2-2T)^2)$ , где — внешний диаметр большего основания, — внешний диаметр меньшего основания, — высота конуса, — толщина стенки*.
После упрощения получаем формулу для объема:
Тогда масса:

5. Масса полой усеченной пирамиды

Для простоты рассмотрим усеченную пирамиду с квадратным основанием. Объем ее стенок: $V={H/3}(A1^2+A1*A2+A2^2-(A1-2T)^2-(A1-2T)(A2-2T)-(A2-2T)^2)$ , где — внешний размер большего основания, — внешний размер меньшего основания, — высота пирамиды, — толщина стенки*.
После упрощения получаем формулу для объема:
Тогда масса:

* в данном случае — это не вполне толщина стенки. Строго говоря, мы имеем тут дело с двумя величинами: та , что стоит в формулах за скобкой, это точно толщина стенки, а та , которую мы отнимаем от внешнего размера тела, чтобы получить его внутренний размер, — это толщина стенки, деленная на косинус угла наклона образующей. Но в большинстве случаев толщина стенки не превышает нескольких процентов от размеров тела, и ошибкой можно пренебречь. Однако, для толстостенных деталей это обстоятельство нужно учитывать.

Источник

Найди верный ответ на вопрос ✅ «Внешний диаметр полого шара 18 см, толщина стенок 3 см. Найдите объём стенок. …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Главная » Геометрия » Внешний диаметр полого шара 18 см, толщина стенок 3 см. Найдите объём стенок.

Источник

Лучший ответ

Ярославна Бершак

Мудрец

(15552)

14 лет назад

V(шара) =4/3ПиR^3
V(стенок) = V(шара) -V(внутреннего пространства)
внешний R=18/2=9
V(внешний) =4/3Пи9^3=972Пи
внутренний R=(18-6)/2=6
V(внутренний) =4/3Пи6^3 = 288Пи
V(стенок) =972Пи – 288Пи = 684Пи
Ответ: объём стенок равен 684Пи

Остальные ответы

Flora Grow

Мастер

(2198)

14 лет назад

вычислить объём шара с радиусом 9 см. потом вычислить объём шара с радиусом 6 см. потом из первого объёма вычесть второй. всё =)

Aleksei

Мудрец

(19451)

14 лет назад

V_стенок = 4/3*pi*(R^3 – (R-h)^3) = 4/3*pi*(9*9*9 – 6*6*6) = 4/3*pi*(729 – 216) = 684*pi

Источник

Тема. «Объёмы тел вращения».

Методическое пособие по решению задач для студентов 2 курса СПО.

Дистанционная форма обучения.

1. Теоретический материал.

Вид круглого тела	Формула объёма
1. Цилиндр	V = R2H
2. Конус	V = R2H
3. Усеченный конус	V = h(R2 + Rr + r2)
6. Шар	V = R3

2. Решение задач.

Задача № 1

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 36 см3.

Дано:

Rц = Rк= R; H ц = H к= H;

Vк = 36 см3

Найти: Vц

Решение.

Vц = R2H; Vк = R2H,

следовательно объем цилиндра в 3 раза больше

объема конуса.

Vц = 3 Vк;

Vц=

Ответ. 108 см3

Задача № 2

Высота одного цилиндра вдвое больше высоты второго цилиндра, но его радиус в два раза меньше радиуса второго цилиндра. Найти отношение их объёмов

Дано:

R1ц = R; Н 1ц = Н; R2ц = 2R;

Н 2ц = Н;

Найти:

Решение.

V1ц = R2H;

V1ц =

Ответ. =

Задача № 3.

Найти объем 25м цилиндрической трубы (полого цилиндра), если внешний радиус равен 50см, диаметр стенок равен 10см.

Дано: полый цилиндр;

R = 50cм = 0,5м; d = 10см = 0,1м

Н = 25м

Найти: V

Решение.

V =Н(R2 – r2); r = R – d; r = 0,5 – 0,1 = 0,4(м)

Ответ. 2,25м3

Задача № 4.

Объём конуса равен 36, а его высота равна 12. Найдите радиус основания конуса.

Дано: конус;

Н=12; V = 36

Найти: R

Решение.

Vк = R2H; 36 =; 4R2=36;

4R2=36; R2 = 36:4 = 9; R = =3

Ответ. 3

Задача № 5

Объем конуса равен 24 см3. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной.

Найдите объем меньшего конуса.

Дано: конус

Vб к = 24см3; SA = SO

Найти: V м к

Решение:

Так как SA = SO, то два конуса подобны.

Коэффициент подобия к =2, следовательно

; ; 8 V м к = 24; V м к = 24:8=3

Или:

Vб к = R2SO V м к = r2SA ; R = 2r; SO=2SA

; ;

8 V м к = 24; V м к = 24:8=3

Ответ. 3

Задача № 6

Диаметр основания конуса равен 16, а длина образующей — 17. Найдите объем конуса.

Дано: конус, D =16; L = 17

Найти: V

Решение:

Vк = R2H;

SAO – прямоугольный, так как SO – высота

конуса, по теореме Пифагора найдем Н.

R = D=8(см)

Н2 = L2 – R 2; Н2 = 172 = 82 =289-64=225;

Н = =15;

Vк =

Ответ.320

Задача № 7

Радиусы оснований усечённого конуса равны 4 и 12, а образующая равна 10. Вычислить объем усечённого конуса.

Дано: усеченный конус;

R=12; r=4; l = 10.

Найти: Vус.к

Решение:

V = h(R2 + Rr + r2)

Высоту усеченного конуса найдем из прямоугольного треугольника АВС (АВ провели параллельно h )

АВ2 = АС2 – ВС2; ВС=R-r=12-4=8

АВ2 = 102 – 82 =100-64=36; АВ=6; h=6

V =

Ответ. 416

Задача № 8

Внутренний диаметр полого шара равен 8 см, а толщина стенок равна 2 см. Найдите объем материала, из которого сделан шар.

Дано: полый шар;

СD = 8см; АС = 2см

Найти: V

Рассмотрим сечение полого шара диаметральной плоскостью.

Решение:

V=V1 – V2; V1=R3; V2=r3; r=СD; R= r +AC

r=СD =(см); R= 4 +2 = 6(см)

Ответ.

Задача № 9

Прямоугольная трапеция с основаниями 11см и 17 см и высотой 12 см вращается около прямой, проходящей через вершину острого угла перпендикулярно основаниям. Hайдите объем полученного тела вращения.

Дано: АВСD – трапеция; ВAD=900; ВС=11см; AD=17 см;

АВ=12 см.

Найти: Vтела вращения

Решение:

При вращении трапеции ABCD получим цилиндр, радиус его основания R = AD =17 см, высотой Н = AB =12 см,

из которого вырезан конус с радиусом основания

r = CM = AD-BC

r =17-11=6 см, высота h=AB=12 см.
Vт.вр.= Vцил. – Vкон

Vцил = R2H; Vцил=;

Vкон =; Vкон =

Vт.вр = 3468-144=3468= 3324(см3)

Ответ. 3324 см3

Задача № 10.

Прямоугольный треугольник с катетами 20 см и 15 см вращается вокруг гипотенузы . Найти объём полученного тела вращения.

Дано:АВС – прямоугольный,

С = 900;

АС=15 см; ВС = 20 см.

Найти: Vтела вращения

Решение:

При вращении прямоугольного треугольника АВС

вокруг гипотенузы получается тело вращения, состоящее из двух конусов с общим основанием.

Радиус R этого основания есть перпендикуляр СО, опущенный из вершины прямого угла на гипотенузу.

Vт.вр.= V1 кон. + V2 кон;

V1 кон. = ; V2 кон. =

Vт.вр.=

По теореме Пифагора найдем гипотенузу АВ

АВ2=АС2+ВС2; АВ2=152+202=225+400=625;

АВ==25 см

Чтобы найти R, из треугольника АВС определим

sin A.

sin A=; sin A= ;

Из прямоугольного треугольника АОС

sin A=; ; ОС=(см); R=12 см

Vт.вр=

Ответ. 1200см3

Задания для самостоятельного решения.

1. Даны две кружки цилиндрической формы. Первая кружка в полтора раза ниже второй, а вторая вдвое шире первой. Во сколько раз объём второй кружки больше объёма первой?

2. Однородный шар диаметром 3 см имеет массу 162 грамма. Чему равна масса шара, изготовленного из того же материала, с диаметром 2 см? Ответ дайте в граммах.

3. Осевое сечение конуса равносторонний треугольник, сторона которого равна 12 см. Найдите объём конуса.

4. Найти объем тела, полученного в результате вращения прямоугольного треугольника вокруг гипотенузы, если катеты равны 3см и 4 см.

5. Прямоугольная трапеция с основанием 5 см и 8 см и высотой 4 см вращается около

большего основания. Найдите объем тела вращения.

Источник

Масса полой детали

1. Масса трубки (полого цилиндра)

2. Масса полого (пустотелого) шара

3. Масса полого сегмента шара

4. Масса полого усеченного конуса

5. Масса полой усеченной пирамиды

Внутренний диаметр полого шара равен 8 см, а толщина стенок равна 2 см. Найдите объем материала, из которого сделан шар.

4. Найти объем тела, полученного в результате вращения прямоугольного треугольника вокруг гипотенузы, если катеты равны 3см и 4 см.

5. Прямоугольная трапеция с основанием 5 см и 8 см и высотой 4 см вращается около

большего основания. Найдите объем тела вращения.

Вам также может понравиться

Как можно исправить кислоту в борще

Как найти загрузочный том

Как найти посылку которую отправили мне

Добавить комментарий Отменить ответ