Как найти объем столба жидкости

Одной из важнейших задач молочной промышленности всегда был учет объема продукта: поступившего на обработку, расходуемого в течение технологического процесса, полученного на выходе. Причем эти измерения требуются как для технологических задач, так и для экономического учета.

О современных способах произведения этих измерений и пойдет речь.Существует несколько подходов к измерению объема жидкости, находящейся в емкости. Все они, однако, имеют одну общую исходную величину, требуемую для расчета. Эта величина – высота столба жидкости.Известна формула, устанавливающая математическую связь между плотностью жидкости, высотой ее столба относительно точки измерения, ускорением свободного падения и давлением, оказываемым на дно и стенки сосуда:

P
=

ρ
×
g
×
h

P= %rho times g times h

где Р – давление, ρ – плотность жидкости, h – высота столба жидкости, g – ускорение свободного падения (9,8 м/c²).

Итак, зная давление и плотность жидкости, нетрудно рассчитать высоту, до которой она доходит относительно точки измерения. Такой способ измерения называется гидростатическим.Для того, чтобы узнать давление жидкости
используются соответствующие датчики. В пищевой промышленности, как правило, это датчики с мембраной, имеющие относительно большую плоскость контакта со средой, что позволяет легко отмывать их от остатков продукта.

Среди датчиков давления наиболее распространены датчики с выходным сигналом 4…20 мА, являющимся общемировым стандартом в системах автоматического управления. Например, интеллектуальный датчик давления 4000-SAN.Сам чувствительный элемент датчика обычно представляет собой тензорезистор – элемент, изменяющий свое сопротивление в зависимости от приложенного к нему усилия. Зависимость сопротивления этих элементов от давления известна. Далее изменение сопротивления электроника датчика приводит к сигналу 4…20 мА.Современные датчики давления часто делаются цифровыми – то есть роль преобразователя играет микроконтроллер, встроенный в датчик. Такие датчики легче настраивать, они обладают более высокой точностью и могут оснащаться дисплеями, модулями коммуникации и дополнительными функциональными возможностями.

Итак, после того, как получено значение высоты, можно переходить к расчету объема жидкости. Выделяются два основных практических подхода:

• геометрическое вычисление;
• аппроксимация линейными отрезками.
  

1. Первый способ измерения объема жидкости: вычисление высоты

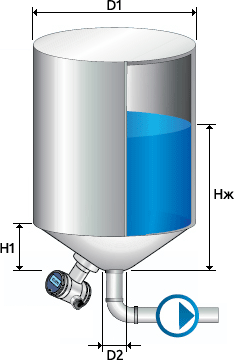
Первый способ подразумевает возможность выражения зависимости высота – объем известной формулой. Он актуален для емкостей, имеющих несложную форму и построенных из таких стандартных геометрических фигур, как, например, полусфера, конус и цилиндр. Например, для широко распространенных емкостей в форме цилиндра с коническим дном (Рисунок 2), вычисление будет производиться следующим образом: до тех пор, пока жидкость не достигла края конуса зависимость ее объема от высоты такова:

V
=

1
3

×
π
×
Hж
×

(

(

R
2

+

K
×
H

)

2

+

(

R
2

+

K
×
H

)

×

R
2

+

R
2
2

)

V= {1} over {3} times %pi times Hж times ( ( R_{2} + K times H )^{2} + ( R_{2} + K times H ) times R _{2} + R_{2} ^{2})

Где V – объем, Нж – высота столба жидкости, K – конусность

K
=

R
1

−

R
2

H
1

K= { R_{1} – R_{2} } over {H_{1}}

как только высота жидкости достигает края конуса и начинает заполнять цилиндр достаточно взять заранее вычисленный полный объем конической части:

Vk
=

1
3

×
π
×

H
1

×

(

R
1
2

+

R
1

×

R
2

+

R
2
2

)

Vk= {1} over {3} times %pi times H_{1} times ( R^{2}_{1} + R_{1} times R_{2} + R^{2}_{2} )

и прибавлять к нему объем жидкости, находящейся в цилиндрической части:

Vц
=

π
×

R
1
2

×

(

Нж
−

H
1

)

Vц= %pi times R_{1}^{2} times ( Нж – H_{1} )

С учетом степени развития микроконтроллеров, подобный алгоритм возможно реализовать непосредственно в датчике. Не нужно никакое внешнее устройство – датчик сам вычислит объем жидкости, если ввести ее плотность и геометрию емкости.Этот способ, однако, имеет определенные недостатки и ограничения. Они будут рассмотрены далее.

2. Точность измерения давления, производимого датчиком

Отдельно нужно отметить требования к точности измерения давления, производимого датчиком. Нетрудно посчитать, что общепромышленный датчик давления, имеющий погрешность в 0,5 % для емкости высотой в 3 метра даст ошибку измерения в:

(

0

,5
×
300

)

100

=

1
,5
см

{ {( 0,5 times 300 )} over {100} } = {1,5 см}

Значение не кажется столь большим. Однако, если емкость при этом имеет диаметр, скажем, в 2 метра, погрешность вычисления объема составит:

V
=
1

,5
×

100
2

×
π

=
47100

см
3

V=1,5 times 100^{2} times %pi =47100 см^{3}

или 47,1 литров.

Достаточно большое значение, с учетом того, что в течение рабочего дня могут производиться десятки циклов наполнения/опустошения емкости. При этом данное значение не учитывает дополнительную погрешность, вызываемую перепадами температуры.Именно поэтому датчики для решения задач вычисления объема обычно имеют погрешность не более 0,1 %. При тех же условиях, такой датчик даст ошибку измерения всего в 9,42 литра, то есть в 5 раз меньшую.

3. Второй способ вычисления: аппроксимация

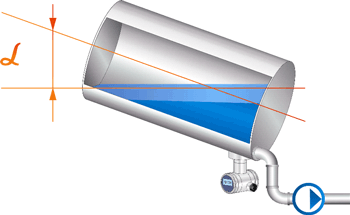
На практике часто встречаются емкости, имеющие искажения формы внутренней поверхности, к которым неприменим геометрический метод вычисления объема емкости.Например, для емкости, установленной под углом (Рисунок 2), наклон в 2…3 градуса, кажущийся незначительным, сильно нарушит точность измерений – в горизонтальной емкости поверхность жидкости вместо прямоугольника будет иметь гораздо более сложную форму, что значительно меняет зависимость объема от уровня.

Емкость может иметь утопленный в стенку люк. В этом случае нужно производить вычисления уже по трем разным формулам, вместо двух. К тому же, зависимость объема на участке с люком будет куда более сложной, чем для
прямого цилиндра. Также, геометрический метод на практике неприменим к емкостям, в которых производится перемешивание продукта.

Массивное устройство внутри емкости значительно исказит результаты вычислений – датчик будет показывать объем, больший, чем реальный. Предусмотреть готовые алгоритмы для каждой подобной ситуации и внести их в
датчик – задача практически невыполнимая. Тут на помощь приходит более трудоемкий, но и значительно более гибкий способ измерения. Если начать заливать в емкость, допустим, по 100 литров жидкости и при этом на каждом шаге отмечать высоту, соответствующую залитому объему, мы получим так называемую «тарировочную таблицу». Суть в следующем: нестандартная форма емкости моделируется с использованием некоторого количества прямых отрезков. Чем их больше, тем точнее будут производиться вычисления. Таким образом, можно высоте столба жидкости поставить в соответствие ее объем.

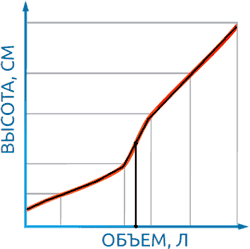
Если жидкость, например, находится посередине между двумя точками, то и объем вычисляется, как среднее значение объемов в этих точках (Рисунок 3). Очевидно, что от количества точек, используемых при тарировании,
значительно зависит точность результата. Если для участка с линейной зависимостью объем/высота достаточно двух точек, до для нелинейных участков их требуется гораздо больше. Тарирование на нелинейном участке можно производить шагами, в два раза большими, чем допустимая погрешность на данном участке. Например, если в конусной части емкости необходимо получить точность не ниже 20 литров, шаги тарирования должны быть не более 40 литров. Тут следует помнить простое правило – чем меньше шаги и больше точек, тем выше итоговая точность работы. Недостаток метода в том, что датчик, перенесенный на другую емкость, снова потребует тарирования. Однако, единожды оттарированный на одной емкости датчик будет не только давать максимально высокую
точность вычислений, но и позволит подсчитывать объем для жидкостей с различными плотностями – достаточно будет лишь ввести в него это значение.

Это значит, что можно произвести тарирование с использованием обычной воды, а затем, предварительно поменяв значение плотности жидкости в памяти датчика, заливать продукт, имеющий плотность, отличную от плотности воды. Таким образом, мы получаем гибкий и точный метод, позволяющий работать с емкостями любой формы и жидкостями любой плотности.

Инженер отдела проектирования ООО «КИП-Сервис»
Горбоносов М.А.

Статика жидкостей и газов.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: давление жидкости, закон Паскаля, закон Архимеда, условия плавания тел.

В гидро- и аэростатике рассматриваются два вопроса: 1) равновесие жидкостей и газов под действием приложенных к ним сил; 2) равновесие твёрдых тел в жидкостях и газах.

Многие из обсуждаемых далее фактов относятся равным образом как к жидкостям, так и к газам. В таких случаях мы будем называть жидкость и газ средой.

При сжатии среды в ней возникают силы упругости, называемые силами давления. Силы давления действуют между соприкасающимися слоями среды, на погружённые в среду твёрдые тела, а также на дно и стенки сосуда.

Сила давления среды обладает двумя характерными свойствами.

1. Сила давления действует перпендикулярно поверхности выделенного элемента среды или твёрдого тела. Это объясняется текучестью среды: силы упругости не возникают в ней при относительном сдвиге слоёв, поэтому отсутствуют силы упругости, касательные к поверхности.

2. Cила давления равномерно распределена по той поверхности, на которую она действует.

Естественной величиной, возникающей в процессе изучения сил давления среды, является давление.

Пусть на поверхность площади действует сила , которая перпендикулярна поверхности и равномерно распределена по ней. Давлением называется величина

.

Единицей измерения давления служит паскаль (Па). 1 Па – это давление, производимое силой 1 Н на поверхность площадью 1 м .

Полезно помнить приближённое значение нормального атмосферного давления: Па.

к оглавлению ▴

Гидростатическое давление.

Гидростатическим называется давление неподвижной жидкости, вызванное силой тяжести. Найдём формулу для гидростатического давления столба жидкости.

Предположим, что в сосуд с площадью дна налита жидкость до высоты (рис. 1). Плотность жидкости равна

Рис. 1. Гидростатическое давление

Объём жидкости равен , поэтому масса жидкости . Сила давления жидкости на дно сосуда – это вес жидкости. Так как жидкость неподвижна, её вес равен силе тяжести:

.

Разделив силу на площадь , получим давление жидкости:

.

Это и есть формула гидростатического давления.

Так, на глубине 10 м вода оказывает давление Па, примерно равное атмосферному. Можно сказать, что атмосферное давление приблизительно равно 10 м водного столба.

Для практики столь большая высота столба жидкости неудобна, и реальные жидкостные манометры – ртутные. Посмотрим, какую высоту должен иметь столб ртути ( кг/м), чтобы создать аналогичное давление:

м = 750 мм.

Вот почему для измерения атмосферного давления широко используется миллиметр ртутного столба (мм рт. ст.).

к оглавлению ▴

Закон Паскаля.

Если поставить гвоздь вертикально и ударить по нему молотком, то гвоздь передаст действие молотка по вертикали, но не вбок. Твёрдые тела из-за наличия кристаллической решётки передают производимое на них давление только в направлении действия силы.

Жидкости и газы (напомним, что мы называем их средами) ведут себя иначе. В средах справедлив закон Паскаля.

Закон Паскаля. Давление, оказываемое на жидкость или газ, передаётся в любую точку этой среды без изменения по всем направлениям.

(В частности, на площадку, помещённую внутри жидкости на фиксированной глубине, действует одна и та же сила давления, как эту площадку ни поворачивай.)

Например, ныряльщик на глубине испытывает давление . Почему? Согласно закону Паскаля вода передаёт давление атмосферы без изменения на глубину , где оно прибавляется к гидростатическому давлению водяного столба .

Отличной иллюстрацией закона Паскаля служит опыт с шаром Паскаля. Это шар с множеством отверстий, соединённый с цилиндрическим сосудом (рис. 2)

Рис. 2. Шар Паскаля

Если налить в сосуд воду и двинуть поршень, то вода брызнет из всех отверстий. Это как раз и означает, что вода передаёт внешнее давление по всем направлениям.

То же самое наблюдается и для газа: если сосуд наполнить дымом, то при движении поршня струйки дыма пойдут опять-таки из всех отверстий сразу. Стало быть, газ также передаёт давление по всем направлениям.

Вы ежедневно пользуетесь законом Паскаля, когда выдавливаете зубную пасту из тюбика. А именно, вы сжимаете тюбик в поперечном направлении, а паста двигается перпендикулярно вашему усилию – в продольном направлении. Почему? Ваше давление передаётся внутри тюбика по всем направлениям, в частности – в сторону отверстия тюбика. Туда-то паста и выходит.

к оглавлению ▴

Гидравлический пресс.

Гидравлический пресс – это устройство, дающее выигрыш в силе. То есть, прикладывая сравнительно небольшую силу в одном месте устройства, оказывается возможным получить значительно большее усилие в другом его месте.

Гидравлический пресс изображён на рис. 3. Он состоит из двух сообщающихся сосудов, имеющих разную площадь поперечного сечения и закрытых поршнями. В сосудах между поршнями находится жидкость.

Рис. 3. Гидравлический пресс

Принцип действия гидравлического пресса очень прост и основан на законе Паскаля.

Пусть – площадь малого поршня, – площадь большого поршня. Надавим на малый
поршень с силой . Тогда под малым поршнем в жидкости возникнет давление:

.

Согласно закону Паскаля это давление будет передано без изменения по всем направлениям в любую точку жидкости, в частности – под большой поршень. Следовательно, на большой поршень со стороны жидкости будет действовать сила:

.

Полученное соотношение можно переписать и так:

.

Мы видим, что больше во столько раз, во сколько больше . Например, если площадь большого поршня в 100 раз превышает площадь малого поршня, то усилие на большом поршне окажется в 100 раз больше усилия на малом поршне. Вот каким образом гидравлический пресс даёт выигрыш в силе.

к оглавлению ▴

Закон Архимеда.

Мы знаем, что дерево в воде не тонет. Следовательно, сила тяжести уравновешивается какой-то другой силой, действующей на кусок дерева со стороны воды вертикально вверх. Эта сила называется
выталкивающей или архимедовой силой. Она действует на всякое тело, погружённое в жидкость или газ.

Выясним причину возникновения архимедовой силы. Рассмотрим цилиндр площадью поперечного сечения и высотой , погружённый в жидкость плотности . Основания цилиндра горизонтальны. Верхнее основание находится на глубине , нижнее – на глубине (рис. 4).

На боковую поверхность цилиндра действуют силы давления, которые приводят лишь к сжатию цилиндра. Эти силы можно не принимать во внимание.

На уровне верхнего основания цилиндра давление жидкости равно . На верхнее основание действует сила давления , направленная вертикально вниз.

На уровне нижнего основания цилиндра давление жидкости равно . На нижнее основание действует сила давления , направленная вертикально вверх (закон Паскаля!).

Так как , то , и поэтому возникает равнодействующая сил давления, направленная вверх. Это и есть архимедова сила . Имеем:

.

Но произведение равно объёму цилиндра . Получаем окончательно:

. (1)

Это и есть формула для архимедовой силы. Возникает архимедова сила вследствие того, что давление жидкости на нижнее основание цилиндра больше, чем на верхнее.

Формулу (1) можно интерпретировать следующим образом. Произведение – это масса
жидкости , объём которой равен . Но тогда , где – вес жидкости, взятой в объёме . Поэтому наряду с (1) имеем:

. (2)

Иными словами, архимедова сила, действующая на цилиндр, равна весу жидкости, объём которой совпадает с объёмом цилиндра.

Формулы (1) и (2) справедливы и в общем случае, когда погружённое в жидкость или газ тело объёма имеет любую форму, а не только форму цилиндра (конечно, в случае газа – это плотность газа). Поясним, почему так получается.

Выделим мысленно в среде некоторый объём произвольной формы. Этот объём находится в равновесии: не тонет и не всплывает. Следовательно, сила тяжести, действующая на среду, находящуюся внутри выделенного нами объёма, уравновешена силами давления на поверхность нашего объёма со стороны остальной среды – ведь на нижние элементы поверхности приходится большее давление, чем на верхние.

Иными словами, равнодействующая сил гидростатического давления на поверхность выделенного объёма – архимедова сила – направлена вертикально вверх и равна весу среды в этом объёме.

Сила тяжести, действующая на наш объём, приложена к его центру тяжести. Значит, и архимедова сила должна быть приложена к центру тяжести выделенного объёма. В противном случае сила тяжести и архимедова сила образуют пару сил, которая вызовет вращение нашего объёма (а он находится в равновесии).

А теперь заменим выделенный объём среды твёрдым телом того же объёма и той же самой формы. Ясно, что силы давления среды на поверхность тела не изменятся, так как неизменной осталась конфигурация среды, окружающей тело. Поэтому архимедова сила попрежнему будет направлена вертикально вверх и равна весу среды, взятой в объёме . Точкой приложения архимедовой силы будет центр тяжести тела.

Закон Архимеда. На погружённое в жидкость или газ тело действует выталкивающая сила, направленная вертикально вверх и равная весу среды, объём которой равен объёму тела.

Таким образом, архимедова сила всегда находится по формуле (1). Заметим, что в эту формулу не входят ни плотность тела, ни какие-либо его геометрические характеристики – при фиксированном объёме величина архимедовой силы не зависит от вещества и формы тела.

До сих пор мы рассматривали случай полного погружения тела. Чему равна архимедова сила при частичном погружении? На ту часть тела, которая находится над поверхностью жидкости, никакая выталкивающая сила не действует. Если эту часть мысленно срезать, то величина архимедовой силы не изменится. Но тогда мы получим целиком погружённое тело, объём которого равен объёму погружённой части исходного тела.

Значит, на частично погружённое в жидкость тело действует выталкивающая сила, равная весу жидкости, объём которой равен объёму погружённой части тела. Формула (1) справедлива и в этом случае, только объём всего тела нужно заменить на объём погружённой части погр:

погр.

Архимед обнаружил, что целиком погружённое в воду тело вытесняет объём воды, равный собственному объёму. Тот же факт имеет место для других жидкостей и газов. Поэтому можно сказать, что на всякое тело, погружённое в жидкость или газ, действует выталкивающая сила, равная весу вытесненной телом среды.

к оглавлению ▴

Плавание тел.

Рассмотрим тело плотности и жидкость плотности . Допустим, что тело полностью погрузили в жидкость и отпустили.

С этого момента на тело действуют лишь сила тяжести и архимедова сила . Если объём тела равен , то

.

Имеются три возможности дальнейшего движения тела.

1. Сила тяжести больше архимедовой силы: , или . В этом случае тело тонет.

2. Сила тяжести равна архимедовой силе: , или . В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.

3. Сила тяжести меньше архимедовой силы: , или . В этом случае тело всплывает, достигая поверхности жидкости. При дальнейшем всплытии начнёт уменьшаться объём погружённой части тела, а вместе с ним и архимедова сила. В какой-то момент архимедова сила сравняется с силой тяжести (положение равновесия). Тело по инерции всплывёт дальше, остановится, снова начнёт погружаться. . . Возникнут затухающие колебания, после которых тело останется плавать в положении равновесия (), частично погрузившись в жидкость.

Таким образом, условие плавания тела можно записать в виде неравенства: .

Формула вычисления объема жидкости в горизонтальном цилиндре сводится к вычислению площади, занимаемой жидкостью в сечении цилиндра. Она имеет форму кругового сегмента (синяя часть рисунка). Для определения площади используют формулу площади кругового сектора (красная и синяя часть) и вычитают из неё площадь треугольника АОВ

Площадь сектора

где альфа — это угол дуги в радианах её можно выразить как

где h – высота уровня жидкости DE.

Площадь равнобедренного треугольника АОВ определяем по классической формуле площади треугольника — произведение половины основания треугольника на его высоту.

Основание АВ найдём по удвоенному катету АЕ, который вычисляем по теореме Пифагора:

Получаем площадь треугольника АОВ:

Теперь, чтобы определить объём, нужно из площади кругового сектора вычесть площадь треугольника и умножить на длину цилиндра L:

---

Если рассмотреть формулу, предложенную на сайте:

то подставив вместо а и b радиус R и преобразовав её, мы получим ту же самую формулу, которая выведена выше.

---

Интересная формула, которая мелькнула на одном из форумов, вполне рабочая:

Она была опробована в Excel, только при h=d (полная ёмкость) получаем ошибку, но её можно устранить через функцию IF((/= h d)…

Запись в Excel выглядит так:

=A3*A1^2*(0,5*ATAN(К­ОРЕНЬ(A2/(A1-A2)))+КОРЕНЬ(A2/(A1-A2))/2/(A1/(A1-A2))-КОРЕНЬ(A2/(A1-A2))/(A1/(A1-A2))^2)

Здесь А1 – диаметр цилиндра d; А2 – высота жидкости h; A3 – длина цилиндра l.

Что такое вместимость сосуда

Вместимость сосуда — это объем его внутренней полости, определяемый по его геометрическим параметрам. Единица измерения объема в СИ — кубический метр, но в случае жидкости чаще используют литр.

Особенности расчета объема жидкости в сосуде

Жидкость по своим свойствам занимает промежуточное место между двумя другими агрегатными состояниями вещества — твердым и газообразным. Жидкости присущи некоторые свойства и твердого тела, и газа. Силы взаимного притяжения молекул в жидкостях достаточно велики, чтобы удерживать молекулы вместе, так что, в отличие от газов, жидкости имеют постоянный собственный объем.

В то же время эти силы недостаточны, чтобы держать молекулы в жесткой упорядоченной структуре, и потому у жидкостей нет постоянной формы: они принимают форму сосуда, в котором находятся.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Жидкость в сосуде оказывает постоянное давление на его стенки, поэтому на производстве, где необходимо регулярно измерять текущий объем жидкости в сосуде, часто используют гидростатические датчики давления.

За счет маленького диаметра их мембран итоговая погрешность измерения близится к нулю. Поэтому, зная давление в конкретный момент времени, можно вычислять уровень жидкости, т. е. высоту гидростатического столба. В формулу для расчета входят только плотность жидкости и ее давление:

(h = frac{p}{rho times g}.)

(p) здесь — давление в паскалях, (rho) — плотность, (g) — ускорение свободного падения, константа.

Зная габариты сосуда, несложно рассчитать объем жидкости в нем. Это необходимо, например, в пивоварении и виноделии, где обычно используются цилиндрические емкости с конусным дном, близкие по параметрам к идеальным геометрическим телам.

При решении логических учебных задач на переливание жидкости из одного сосуда в другой может пригодиться понимание взаимосвязи объема жидкости и параметров сосуда. А для задач по физике часто требуется рассчитать объем, который занимает жидкость в сосуде, через ее массу. На практике это действительно один из самых удобных способов, не требующий ни специальных датчиков, ни сложных расчетов. 

Решение:

Плотность керосина можно узнать из справочной таблицы — 800 (frac{кг}{м^{3}}.)
Вычислим массу керосина в сосуде: 600 – 440 = 160.
Подставим известные данные в формулу:

(V = frac{m}{rho} = frac{0,16}{800} = 0,0002 м^{3} = 200 см^{3}.)

Ответ: 200 (см^{3}.)

Как определить вместимость сосудов разных форм

Вычисление объема параллелепипеда

Параллелепипед — это призма, объемная шестигранная фигура, в основании которой находится параллелограмм.

(V = S_{осн} times H. )

Прямоугольный параллелепипед — это призма, у которой все грани являются прямоугольниками. Прямоугольный параллелепипед, все грани которого являются квадратами, — это куб.

Чтобы вычислить объем прямоугольного параллелепипеда, достаточно найти произведение трех его измерений:
 

(V = AB times AD times AA_{1} = abc.)
Объем куба равен кубу его стороны:
(V = a^{3}.)

Нахождение объема пирамиды

Пирамида — это многогранник, состоящий из основания — плоского многоугольника, вершины — точки, лежащей не в плоскости основания, и отрезков, которые соединяют вершину с углами основания. Высота пирамиды — это перпендикуляр, опущенный из вершины на плоскость основания.

(V = frac{1}{3} times S_{осн} times h.)

Чтобы определить объем усеченной пирамиды, надо знать площадь обоих оснований — (S_{1}) и (S_{2}).

(V = frac{1}{3} times h times (S_{1} + S_{2} + sqrt{S_{1} times S_{2}}). )

Как найти объем цилиндра

Цилиндр — это тело, состоящее из двух кругов, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.

(R) — радиус основания цилиндра, (h) — его высота, равная образующей оси.
(V = S_{осн} times h = pi times R^{2} times h.)

Если нужно найти объем усеченного цилиндра, то понадобится не только R — радиус основания, но и наибольшая и наименьшая образующие. Они обозначаются буквой l — (l_{1}) и  (l_{2}).
(V = pi times R^{2} times frac{l_{1} + l_{2}}{2}.)

Как высчитать объем конуса

Конус — это тело, состоящее из круга, точки, лежащей не в плоскости этого круга, и отрезков, которые соединяют вершину с точками основания.

(V = frac{1}{3} times S_{осн} times h = frac{1}{3} times pi times R^{2} times h.)

Чтобы найти объем усеченного конуса, понадобятся (R_{1}) и (R_{2}) — радиусы оснований, а также высота (h).

(V = frac{pi times h}{3} times (R_1^2 + R_2^2 + R_1 times R_2).)

Нахождение объема шара

Шар — это тело, состоящее из всех точек пространства, находящихся на расстоянии не больше заданного радиуса от центральной точки.

(R) — радиус полукруга, равный радиусу шара.
(V = frac{4pi times R^{3}}{3}.)