Как найти объем сухого воздуха

Теоретический объем воздуха и дымовых газов. Настройка горелки газоанализатором TESTO 320vid

vid

Топливо для котельных агрегатов

Жидкое топливо (котельный мазут)

Твердое топливо и его классификация

Газовое топливо

Снижение выбросов окислов серы

Расчет трубопроводов

Экономия тепловой энергии на предприятии

Котельные установки с паровыми и водогрейными котлами и их компоновка

Состав котельной установки

Технологическая схема производства тепла в котельной

Устройство котельных помещений

Вода для питания паровых и водогрейных котлов

Характеристика природных вод и требования к качеству питательной воды

Подготовка воды для питания котлов

Деаэрация питательной и подпиточной воды для питания котлов

Водный режим котельных агрегатов

Горение топлива

Теоретический объем воздуха и дымовых газов

Коэффициент избытка воздуха

Энтальпия воздуха и продуктов сгорания

Тепловой баланс котельных агрегатов

Коэффициент полезного действия КПД котельных агрегатов

Составные части теплового баланса котельного агрегата

Если известен элементарный состав рабочей массы топлива, можно теоретически определить количество воздуха, необходимого для горения
топлива, и количество образующихся дымовых газов.

Количество воздуха, необходимое для горения, вычисляют в кубических метрах при нормальных условиях (0°С и 760 мм рт. ст):

для 1 кг твердого или жидкого топлива и

для 1 м³ газообразного.

Теоретический объем сухого воздуха. Для полного сгорания 1 кг твердого и жидкого топлива теоретически необходимый объем воздуха, м³/кг, находят делением массы израсходованного кислорода на плотность кислорода при нормальных условиях ρ^Н_О2

= 1,429 кг/м3 и на 0,21, так как в воздухе содержится 21% кислорода

Для полного сгорания 1 м³ сухого газообразного топлива необходимый объем воздуха, м3/м3,

В приведенных формулах содержание элементов топлива выражается в процентах по массе, а состав горючих газов СО, Н₂, СН₄ и др. — в процентах по объему; СmНn — углеводороды, входящие в состав газа, например метан СН₄ (m = 1, n = 4), этан С₂Н₆ (m = 2, n = 6) и т. д. Эти цифровые обозначения составляют коэффициент (m + n/4)

Пример 5. Определить теоретическое количество воздуха, необходимое для сгорания 1 кг топлива следующего состава: С^р=52,1%; Н^р=3,8%;
S^р₄=
2,9%; N^р=1,1%;
O^р=9,1%

Подставляя эти величины в формулу (27), получим
V°_B
= 0,0889 (52,1 + 0,375 • 2,9) + 0,265 • 3,8

—–
0,0333 • 9,1 = 5,03 м3/кг.

Пример 6. Определить теоретическое количество воздуха, необходимое для горения 1 м3 сухого газа следующего состава:

СН₄ = 76,7%; С₂Н₆=4,5%;
С₃Н₈ = 1,7%; С₄Н₁₀ = 0,8%; С5Н12
= 0,6%; Н₂= 1%; С0₂=0,2%; К, = 14,5%.

Подставляя числовые значения в формулу (29), получим

    Теоретический объем дымовых газов. При полном сгорании топлива дымовые газы, уходящие из топки, содержат: двуокись углерода СО₂, пары Н₂О (образующиеся при сгорании водорода топлива), сернистый ангидрид SО₂,
азот N₂ — нейтральный газ, поступивший в топку с кислородом воздуха, азот из состава топлива Н₂, а также кислород избыточного воздуха О₂. При неполном сгорании топлива к указанным элементам добавляются еще окись
углерода СО, водород Н₂ и метан СН₄. Для удобства подсчетов продукты сгорания разделяют на сухие газы и водяные
пары.

Объем сухих газов принимают за 100%. При полном сгорании топлива состав сухих продуктов сгорания (в процентах по объему) следующий:

Газообразные продукты сгорания состоят из трехатомных газов СО₂ и SО₂, сумму которых принято обозначать символом RO₂, и двухатомных газов — кислорода О₂ и азота N₂.

Тогда равенство будет иметь вид:

при полном сгорании

R0₂ + 0₂ + N₂ = 100%,          (31)

при неполном сгорании

R0₂ + 0₂ + N₂ + СО = 100%;

Объем сухих трехатомных газов находится делением масс газов СО₂ и SО₂ на их плотность при нормальных условиях.

Объем газов, получающийся при сжигании 1 кг топлива, определяется по реакциям горения и их выражениям в киломолях

Рсо₂ = 1,94 и Psо₂ = 2,86 кг/м3 — плотности двуокиси углерода и сернистого газа при нормальных условиях.

 

Объем воздуха,
объем и масса продуктов сгорания
определя­ются на 1 кг твердого, жидкого
или на 1 м³
сухого газообраз­ного топлива при
нормальных условиях.

Объем воздуха,
необходимый для сгорания топлива.
Теорети­ческий (при коэффициенте
избытка воздуха в топке α_т=1)
объем сухого воздуха (м³/кг),
необходимый для полного сгорания 1 кг
твердого или жидкого топлива, определяется
по формуле

V⁰=0,089C^p+0,226H^p+0,033(S-O^p). (1.27)

Теоретический
объем воздуха (м³/м³),
необходимый для пол­ного сгорания 1
м³
сухого газообразного топлива, определяется
по формуле

V⁰=0,0478[0,5(CO+H₂)+1,5H₂S+2CH₄+Σ(m+n/4)C_mH_n-O₂]. (1.28)

В формуле (1.27)
содержание элементов топлива выражается
в процентах на 1 кг массы топлива, а в
(1.28) содержание горю­чих газов СО, Н₂,
H₂S,
СН₄
и т. д. — в процентах по объему.

Для сгорания смеси
двух твердых, жидких или газообразных
топлив теоретический объем сухого
воздуха определяется по формуле

V=b₁V+(1-b₁)
V, (1.29)

где b₁
— массовая
доля одного из топлив в смеси.

Действительный
объем воздуха (м³/кг,
м³/м³),
поступивший в топку, определяется по
формуле

V_д=α_тV⁰,
(1.30)

где α_т—
коэффициент избытка воздуха в топке.

Состав и
объем
продуктов сгорания
топлива. При
полном сгорании топлива продукты
сгорания содержат газы: СО₂,
SO;
N₂,
О₂
и пары воды Н₂О,
т. е.

CO₂+SO₂+N₂+O₂+H₂O=100%.

Полный объем
продуктов сгорания V_г(м³/кг)
представляет собой сумму объемов сухих
газов V_cг
и водяных
паров V_HгO:

V_г=V_сг+V_HгO, (0.31)

при этом

V_сг=V_ROг+V_Nг+V_Oг

где V_ROг=V_COг+V_SOг
— объем
трехатомных газов, м³/кг;
V_Nг+V_Oг
— объем двухатомных газов, м³/кг.

Для твердых (кроме
сланцев) и жидких топлив теоретические
объемы (м³/кг)
продуктов полного сгорания при
α_т=1
определяются по формулам:

объем двухатомных
газов

; (1.32)

объем трехатомных
газов

V_ROг=0,0187(C^P+0,375S); (1.33)

объем сухих газов

V=V_ROг+=0,0187(C^P+0,375S) (1.34)

объем водяных
паров

V=0,0124(9H^p+W^p)+0,0161V⁰; (1.35)

полный объем
продуктов сгорания

V=V+V=0,0187(C^P+0,375S)+0,0124(9H^p+W^p)+0,0161V⁰.

(1.36)

Для сланцев объем
трехатомных газов определяется по
формуле

V=V+[0,509(СО₂)/100]
K=0,0187
(C^p+0,375S)+[0,509(CO₂)/l00]К, (1.37)

где K
— коэффициент разложения карбонатов:
при слоевом сжи­гании К=0,7,
при камерном
— 1,0.

Для газообразного
топлива теоретические объемы продуктов
сгорания (м³/м³)
при α_т=1
определяются по формулам:

объем двухатомных
газов

; (1.38)

объем трехатомных
газов

V=
0,01[CO₂+CO+H₂S+ΣmC_mH_n]; (1.39)

объем сухих газов

V=V+V; (1.40)

объем водяных
паров

V=0,01[H₂S+H₂+Σ(n/2)С_mН_n+0,124d_г]+0,0161V⁰, (1.41)

где d_г
— влагосодержание
газообразного топлива, отнесенное к 1
м³
сухого газа, г/м³;

полный объем
продуктов сгорания

V=V+V. (1.42)

Для твердых (кроме
сланцев), жидких и газообразных топлив
объемы продуктов полного сгорания
(м³/кг)
при α_т
>1 определя­ются по формулам:

объем сухих газов

V_сг=V+(α_т-1)V⁰=V+V+(α_т-1)V⁰; (1.43)

объем водяных
паров

V=V+0,0161(α_т-1)V⁰; (1.44)

полный объем
продуктов сгорания определяется по
формуле (1.31).

Для сланцев полный
объем продуктов сгорания (м³/кг)
при α_т
>1:

V_гк=V+V+V=V+V+0,0124(9H^p+W^p)+0,0161α_тV⁰. (1.45)

Содержание (%) СО₂,
SO₂
и RO₂
в сухих газах при полном сгорании топлива
определяется по формулам:

CO₂=(V/V_cг)100; (1.46)

SО₂=(
V/V_cг)100; (1.47)

RО₂=(V/V_cг)100. (1.48)

Максимальное
содержание (%) трехатомных газов ROв сухих газах при полном сгорании топлива

RO=21/(l+β), (1.49)

где β
— характеристика
топлива:

для твердого и
жидкого

β
=2,35(H^p-0,126O^p+0,04N^p)/(C^p+0,375S); (1.50)

для газообразного

(1.51)

Содержание (%) азота
N₂
и кислорода О₂
в сухих газах при
полном
сгорании топлива

N₂=100-RO₂-O₂; (1.52)

O₂=21-βRO₂-RO₂. (1.53)

Масса продуктов
сгорания:

для твердого (кроме
сланцев) и жидкого топлива (кг/кг)

М_г=1-0,01А^р+1,306α_тV⁰; (l.54)

для газообразного
топлива (кг/м³)

Мг=+0,001d_гт+1,306α_тV⁰, (1.55)

где
— плотность сухого газа, кг/м³;
d_гт
— содержание влаги в топливе, кг/м³;

для сланцев (кг/кг)

M_гк=1-0,01А+1,306α_тV⁰+0,01(СО₂)К, (1.56)

где А
— расчетное
содержание золы в топливе с учетом
неразложившихся карбонатов, %; К
— коэффициент
разложения кар­бонатов: при слоевом
сжигании К=0,7,
при камерном
— 1,0.

Расчетное содержание
(%) золы в топливе с учетом неразложившихся
карбонатов

А=А^р+(1-К)(СО₂). (1.57)

Для твердых топлив
концентрация золы в продуктах сгорания
определяется по формуле

μ_зл=А^ра_ун/(100М_г), (1.58)

где а_ун
— доля золы топлива, уносимой продуктами
сгорания.

Коэффициент
избытка воздуха в топке.
При полном сгорании топлива коэффициент
избытка воздуха в топке определяется
по формуле

, (1.59)

где О₂
и N₂
— содержание кислорода и азота в газах,
%.

Задача 1.27.
Определить
объем продуктов полного сгорания на
выходе из топки, а также теоретический
и действительный объемы воздуха,
необходимые для сгорания 1 м³
природного
газа Ставропольского месторождения
состава: СО₂=0,2%;
СН₄=98,2%;
С₂Н₆=0,4%;
С₃Н₈=0,1%;
С₄Н₁₀=0,1%;
N₂=l,0%.
Коэффициент избытка воздуха в топке
α_т=1,2.

Решение:
Теоретический объем воздуха, необходимый
для полного сгорания 1 м³
топлива, определяем по формуле (1.28)

V⁰=0,0478[0,5CO+0,5H₂+1,5H₂S+2CH₄+Σ(m+n/4)C_mH_n-O₂]=
=0,0478(2·98,2+3,5·0,4+5·0,1+6,5·0,1)=9,51
м³/м³.

Действительный
объем воздуха по формуле (1.30)

V_д=α_тV⁰=1,2·9,51=11,41м³/м³.

Объем сухих газов
при α_т=1,2,
по формуле (1.43),

V_сг=V+(α_т-1)V⁰=V+V+(α_т-1)V⁰=
=0,01(0,2+98,2+2·0,4+3·0,1+4·0,1)+0,79·9,51+1,0/100+(1,2-1)9,51=10,42
м³/м³.

Объем водяных
паров при α_т=1,2,
по формуле (1.44),

V=0,01(H₂S+H₂+2CH₄+3C₂H₆+4C₃H₈+5С₄Н₁₀+0,124d_г)+0,0161α_тV⁰=
=0,01(2·98,2+3·0,4+4·0,1+5·0,1)+0,0161·1,2·9,51=2,17
м³/м³.

Объем продуктов
полного сгорания, по формуле (1.31),

V_г=V_сг+V=10,42+2,17=12,59
м³/м³.

Задача 1.28.
Определить
на выходе из топки объем продуктов
полного сгорания
1 кг карагандинского
угля марки К ее става: С^р=54,7%;
Н^р=3,3%;
S=0,8%;
N^p=0,8%;
O^p=4,8%,
А^р=27,6%;
W^p=8,0%.
Коэффициент избытка воздуха в топке
α_т=1,3.

Решение:
Теоретический объем воздуха, необходимый
дл полного сгорания 1 кг топлива,
определяем по формуле (1.27):

V₀=0,089C^p+0,266Н^р+0,033(S–О^р)=0,089·54,7+0,266·3,3+0,033(0,8-4,8)=5,61
м³/кг.

Объем сухих газов
при α_т=1,3,
по формуле (1.43),

V_сг=V+V+(α_т-1)V⁰=0,0187(C^p+0,375S)+0,79V⁰+0,8N^p/100+(α_т-l)V⁰=
=0,0187(54,7+0,375·0,8)+0,79·5,61+0,8·0,8/100+(1,3-1)·5,61=7,15
м³/кг.

Объем водяных
паров при α_т=1,3,
по формуле (1.44),

V=V+0,0161(α_т-1)V⁰=0,0124(9H^p+W^р)+0,0161α_тV⁰=
=0,0124(9·3,3+8)+0,0161·1,3·5,61=0,58
м³/кг.

Объем продуктов
полного сгорания, по формуле (1.31),

V_г=V_cг+V=7,15+0,58=7,73
м³/кг.

Задача 1.29.
Определить
теоретический и действительный объемы
воздуха, необходимые для слоевого
сжигания 1000 кг донецкого угля марки Г
состава: С^р=55,2%;
Н^р=3,8%;
S=3,2%;
N^р=1,0%;
О^р=5,8%;
А^р=23,0%;
W^p=8,0%.
Коэффициент избыт­ка воздуха в топке
α_т=1,3.

Ответ: V₀
= 5830 м³;
V_д=7579
м³.

Задача 1.30.
Определить объем воздуха, необходимый
для сжигания 800 кг/ч ленгерского угля
марки БЗ состава: С^р=45,0%;
Н^р=2,6%;
S=l,7%;
N^p=0,4%;
О^р=9,9%;
A^р=11,4%;
W^p=29,0%,
и 500 кг/ч экибастузского угля марки СС
состава: С^р=43,4%;
Н^р=2,9%;
S=0,8%;
N^p=0,8%;
O^p=7,0%;
A^р=38,1%;
W^p=7,0%,
при коэффициентах избытка воздуха в
то­почной камере соответственно
α_т=1,4
и 1,3.

Ответ: V_д=7823
м³/ч.

Задача 1.31.
Определить теоретический и действительный
объемы воздуха, необходимые для сжигания
2000 м³/ч
природ­ного газа Ставропольского
месторождения состава: СО₂=0,5%;
СН₄=92,8%;
С₂Н₆=2,8%;
С₃Н₈=0,9%;
С₄Н₁₀=0,4%;
С₅Н₁₂=0,1%;
N₂=2,5%;
и 1000 м³/ч
природного газа Ленин­градского
месторождения состава: CO₂=0,1%;
СН₄=89,7%;
С₂Н₆=5,2%;
С₃Н₈=1,7%;
С₄Н₁₀=0,5%;
С₅Н₁₂=0,1%;
N₂=2,7%,
при коэффициентах избытка воздуха в
топочной камере соответ­ственно
α_т=1,15
и 1,1.

Ответ: V₀=29360
м³/ч;
V_д=33264
м³/ч.

Задача 1.32.
Определить теоретический и действительный
объемы воздуха, необходимые для слоевого
сжигания 2000 кг кузнецкого угля марки
Д, если известен состав его горючей
массы: C^г=78,5%;
Н^г=5,6%;
S=
0,4%; N^г=2,5%;
O^г=13,0%,
зольность сухой массы А^с=15,0%
и влажность
рабочая W^p=12,0%.
Коэффициент избытка воздуха в топочной
камере α_т=1,3.

Ответ:
V₀=
12 040 м³;
V_д
=15 652 м³.

Задача 1.33.
Определить теоретический объем воздуха,
необ­ходимый для слоевого сжигания
1500 кг ленинградских сланцев, если
известен состав их горючей массы:
С^г=74,0%;
Н^г=9,5%;
S=6,l%;
N^г=0,4%;
О^г=10,0%;
А^р=46,0%;
W^p=11,5%
и(СО₂)=16,4%.

Ответ: V₀=3765
м³.

Задача 1.34.
В топке котла
сжигается смесь, состоящая из 2·10³
кг кузнецкого угля марки Д состава:
C=58,7%;
Н=4,2%;
(S)₁=0,3%;
N=l,9%;
O=9,7%;
A=13;2%;
W=12,0%,
и 3·10³
кг кузнецкого угля марки Г состава:
С=66Д%;
Н=4,7%;
(S)₂=0,5%;
N=1,8%;
O=7,5%;
А=11,0%;
W=8,5%.
Определить
теоретический объем сухого воздуха,
необходимый для сгорания смеси.

Ответ: V=32700
м³.

Задача 1.35. В
топке котла сжигается воркутинский
уголь марки Ж состава: С^p=59,6%;
Н^р=3,8%;
S=0,8%;
N^p=l,3%;
О^р=5,4%;
A^р=23,6%;
W^p=5,5%.
Определить объем сухих газов при полном
сгорании топлива. Коэффициент избытка
воздуха в топке α_т=1,3.

Ответ: V_сг=7,84
м³/кг.

Задача 1.36.
Определить
объем водяных паров при полном сгорании
в слое 10 кг/ч фрезерного торфа состава:
С^р=24,7%
Н^р=2,б%;
S=0,l%;
N^p=l,l%;
О^р=15,2%;
А^р=6,3%;
W^р=50,0%
при коэффициентах избытка воздуха в
топке α_т=1,3
и 1,4.

Ответ: V=963
м³/ч;
V=965
м³/ч.

Задача 1.37.
В топке котла
сжигается 600 м³
природного газа Угерского месторождения
состава: СО₂=0,2%;
СН₄=98,5%;
С₂Н₆=0,2%;
С₃Н₈=0,1%;
N₂=l,0%.
Определить объем продуктов сгорания
при коэффициенте избытка воздуха в
топке α_т=1,3.

Ответ: V_г=7210
м³.

Задача 1.38.
Определить
объем сухих газов, получаемых при полном
сгорании в слое 800 кг кузнецкого угля
марки Д, если известен состав его горючей
массы: C^г=78,5%;
Н^г=5,6%;
S=0,4%;
N^г=2,5%;
О^г=13,0%;
зольность сухой массы А^г=15,0%
и влажность рабочая W^p=12,0%.
Коэффициент избытка воздуха в топке
α_т=1,3.

Ответ: V_cг=6141
м³.

Задача 1.39.
Определить
объем двух- и трехатомных газов и
содержание СО₂
и SO₂
в сухих газах, получаемых при полном
сгорании 1 кг донецкого угля марки Т
состава: С^р=62,7%;
Н^р=3,1%;
S=2,8%;
N^p=0,9%;
О^р=1,7%;
А^р=23,8%;
W^p=5,0%
если известно, что дымовые газы при
полном сгорании содержат RO=18,8%.

Решение:
Объем трехатомных газов определяем по
форму (1.33):

V=V+V=0,0187(С^p+0,375S)=0,0187(62,7+
0,375·2,8)=1,19 м³/кг.

Объем сухих газов
находим по формуле (1.48):

=
6,33 м³/кг.

Объем двухатомных
газов V=V_cг–V=
6,33-1,19=5,14
м³/кг.

Содержание СО2 в
сухих газах определяем по формуле
(1.46):

CO₂=(V/V_cг)100=(0,0187С^р/V_cг)100=(0,0187·62,7/6,33)100=18,5%.

Содержание SO₂
в сухих газах находим по формуле (1.47):

SO₂==(V/V_cг)100=(0,0187·0.375S/V_cг)100=(0,0187·0.375·2,8/6,33)100=0,31%.

Задача
1.40. Определить
объем трехатомных газов и содер­жание
в них СО₂
и SO₂,
получаемых при полном сгорании 1 кг
ткибульского угля марки Г состава:
С^р=45,4%;
Н^р=3,5%;
S=1,3%;
N^p=0,9%;
О^p=8,9%;
A^р=27,0%;
W^p=13,0%,
если из­вестно, что дымовые газы
содержат RO=18,7%.

Ответ:
V=0,86
м³/кг;
СО₂=18,5%;
SO₂=0,2%.

Задача 1.41.
Определить объем сухих дымовых газов,
получа­емых при сжигании 1000 кг
фрезерного торфа состава: С^р=24,7%;
Н^р=2,6%;
S=0,1%;
N^p=l,l%;
O^p=15,2%;
A^р=6,3%;
W^p=50,0%,
если известно, что дымовые газы при
полном сгорании топлива содержат
RO₂=15,0%.
Коэффициент избытка воздуха в топке
α_т=
1,3.

Ответ: V_cг=3066
м³.

Задача 1.42. В
топке котла сжигается 5·10³
кг/ч донецкого угля марки Г состава:
С^р=0,2%;
Н^р=3,8%;
S=3,2%;
N^p=l,0%;
О^р=5,8%;
А^р=23,0%;
W^p=8,0%.
Определить, на сколько был увеличен
объем подаваемого в топку воздуха, если
известно, что при полном сгорании топлива
содержание RO₂
в дымовых газах снизилось с 16 до 14%.

Ответ: V_в=5949
м³/ч.

Задача 1.43. В
топке котла сжигается 2·10³
кг/ч малосерни­стого мазута состава:
С^р=84,65%;
Н^р=11,7%;
S=0,3%;
О^р=0,3%;
А^р=0,05%;
W^p=3,0%.
Определить, на сколько был увеличен
объем подаваемого в топку воздуха, если
известно, что при полном сгорании топлива
содержание RO₂
в дымовых газах снизилось с 15 до 12%.

Ответ:
V_в=
6666 м³/ч.

Задача 1.44.
В топке котла
во время испытаний сожжено 3·10³
кг/ч кузнецкого угля марки Д состава:
С^p=58,7%;
Н^р=4,2%;
S=0,3%;
N^p=l,9%;
О^р=9,7%;
A^р=13,2%;
W^p=12,0%.
В течение первой половины испытаний в
продуктах полного сгорания топлива
получено RO₂=18%,
а в течение вто­рой половины испытаний
RO₂
уменьшилось до 15%. Определить, какой
объем воздуха добавлен в топку между
первой и второй половинами испытаний.

Ответ:
V_в=
4650 м³/ч.

Задача
1.45. Определить
объем продуктов сгорания, получаемых
при полном сгорании 1 кг ленинградских
сланцев состава С^р=20,6%;
Н^р=2;7%;
S=l,7%;
N^p=0,l%;
O^p=2,8%;
А^р=46,0%;
W^p=11,5%;
(СО₂)=16,4%.
Коэффициент избытка воздуха в топке
α_т=1,3.

Ответ: V_г
=2,96 м³/кг.

Задача
1.46. Определить
объем продуктов сгорания, получаемых
при полном сгорании 2·10³
кг/ч карагандинского угля марки К
состава: С^р=54,7%;
Н^р=3,3%;
S=0,8%;
N^p=0,8%;
О^р=4,8%;
А^р=27,6%;
W^p=8,0%,
если известно, что дымовые газы содержат
RO₂=18%.

Ответ: V_г=12560
м³/ч.

Задача 1.47.
Определить
максимальное содержание трехатомных
газов в продуктах полного сгорания 1 кг
донецкого угля марки А состава: С^р=63,8%;
Н^р=1,2%;
S=l,7%;
N^p=0,6%;
О^р=1,3%;
А^р=22,9%;
W^p=
8,5%.

Ответ: RO=20,2%.

Задача
1.48. В
топке котла сжигается смесь из 2·10³
кг, донецкого угля марки Д состава:
С=49,3%;
H=3,б%;
(S)₁=3,0%;
N=l,0%;
О=8,3%;
A=21,8%;
W=13,0%
и 3·10³
кг/ч донецкого угля марки Г состава:
С=55,2%;
Н=3,8%;
(S)₂=3,2%;
N=1,0%;
O=5,8%;
A=23%;
W=8%.
Определить
объем газов, получаемых при полно
сгорании смеси, если коэффициент избытка
воздуха в топке α_т=1,3.

Ответ: V_г=37
480 м³/ч.

Задача 1.49.
Определить
объем газов, получаемых при полном
сгорании 1000 м³/ч
природного газа Радченковского мест
рождения состава: СО₂=0,1%;
СН₄=85,8%;
С₂H₆=0,2%;
С₃Н₈=0,1%;
С₄Н₁₀=0,1%;
N₂=13,7%.
Коэффициент избытка воздуха в топочной
камере α_т=1,1.

Ответ: V_г=10
230 м³/ч.

Задача 1.50. В топке
котла сжигается 1 кг артемовско угля
марки БЗ состава: С^р=35,7%;
Н^р=2,9%;
S=0,3%;
N^р=0,7%;
О^р=12,1%;
А^р=24,3%;
W^p=24,0%.
Определить объем продуктов сгорания и
содержание в них кислорода О₂,
если RO₂=18%.

Ответ: V_г=4,16
м³/кг;
О₂=1,3%.

Задача
1.51. В
топке котла сжигается 1 кг анадырского
угля марки БЗ состава: С^р=50,1%;
Н^р=4,0%;
S=0,1
N^p=0,7%;
О^р=12,2%;
А^р=11,9%;
W^p=21,0%.
Определить коэффициент избытка воздуха
при полном сгорании топлива, если RO₂
= 16%.

Ответ: α_т=1,2.

Задача 1.52.
В топке котла сжигается донецкий уголь
марки Т состава: С^р=62,7%;
Н^р=3,1%;
S=2,8%;
N^p=0,9%;
O^p=
l,7%;
А^р=23,8%;
W^p=5,0%.
Определить
содержание азота N₂
в проду­ктах сгорания и коэффициент
избытка воздуха при полном сгора­нии
топлива, если RO₂=15,0%.

Ответ: V=5,09
м³/кг;
α_т=1,26.

Задача 1.53.
Определить объем сухих газов и коэффициент
избытка воздуха при полном сгорании
природного газа Сара­товского
месторождения состава: СО₂=1,2%;
СН₄=91,9%;
С₂Н₆=2,1%;
С₃Н₈=1,3%;
С₄Н₁₀=0,4%;
С₅Н₁₂=0,1%;
N₂=3,0%,
если известно, что продукты сгорания
содержат RO₂=16,0%
и О₂=4,0%.

Ответ: V_сг=6,44
м³/м³;
α_т=1,23.

Задача 1.54. В
топке котла сжигается 1 кг райчихинского
уг­ля марки Б1 состава: С^р=30,4%;
Н^р=1,7%;
S=0,3%;
N^p=0,5%;
О^р=12,2%;
A^р=7,9%;
W^p=47,0%.
Определить содержание кисло­рода О₂
в продуктах сгорания и коэффициент
избытка воздуха при полном сгорании
топлива, если RO₂=16,0%.

Ответ: О₂=4,8
%; α_т=1,3.

Задача 1.55.
Определить
массу продуктов сгорания и концен­трацию
золы в продуктах сгорания, получаемых
при полном сгорании 1 кг ленинградских
сланцев состава: С^р=20,6%;
H^p=2,7%;
S=1,7%;
N^p=0,l%;
О^р=2,8%;
A^р=46,0%;
W^p=11,5%;
(СО₂)=16,4%,
если, известно, что доля золы топ­лива,
уносимой продуктами сгорания, а_ун=0,95.
Коэффициент избытка воздуха в топке
α_т=1,3.

Решение:
Расчетное содержание золы в топливе с
учетом неразложившихся карбонатов
определяем по формуле (1.57):

А=А^р+(1-К)(СО₂)=46,0+(1-0,1)16,4=50,9%.

Теоретический
объем воздуха, необходимый для полного
сго­рания 1 кг топлива, находим по
формуле (1.27):

V⁰=0,089С^р+0,266Н^р+0,033(S-О^р)=0,089·20,6+0,266·2,7+0,033(1,7-2,8)=2,52
м³/кг.

Масса продуктов
сгорания, по формуле (1.56),

M_гк=1-0,01A+1,306α_тV⁰+0,01(СО₂)K=1-0,01·50,9+1,306·1,3·2,52+0,01·16,4·0,7=
=4,9
кг/кг.

Концентрация золы
в продуктах сгорания, по формуле (1.58),

μ_зл=А^ра_ун/(М_гк)=(46·0,95)/(4,9·100)=0,0892.

Задача 1.56.
Определить
массу продуктов сгорания и концентрацию
золы в продуктах сгорания, получаемых
при полном сгорании 1 кг карагандинского
угля марки К состава: С^р=54,7%;
Н^р=3,3%;
S=0,8%;
N^p=0,8%;
О^р=4,8%;
А^р=27,6%;
W^p=8,0%,
если известно, что доля золы топлива,
уносимой продуктами сгорания, а_ун=0,85.
Коэффициент избытка воздуха в топке
α_т=1,3.

Ответ: М_г=9,25
кг/кг; μ_зл=0,0253.

Задача 1.57.
Определить
массу продуктов сгорания, получаемых
при полном сгорании 1 м³
природного газа Ставропольского
месторождения состава: СО₂=0,2%;
СН₄=98,2%;
С₂Н₆=0,4%;
С₃Н₈=0,1%;
С₄Н₁₀=0,1%;
N₂=l,0%,
если известно, что плотность сухого
газа ρ=0,728
кг/м³.
Коэффициент избытка воздуха в топке
α_т=1,15.

Ответ: М_г=15
кг/м³.

Объем – сухой воздух

Cтраница 1

Объемы сухого воздуха и водяных паров, а также их температуры приняты одинаковыми.
 [1]

Вычислить, какой объем сухого воздуха был растворен в воде при условиях опыта. Как изменяется растворимость газов с изменением давления.
 [2]

В трубку 5 вводят такой объем сухого воздуха, чтобы при температуре и барометрическом давлении, отвечающими времени установки нитрометра, он равнялся после отнесения к нормальным условиям ( к 0 и 760 мм давления) объему в 100 мл. Для этого, открыв кран 11, соединяют трубку 3 с воздухом через колонку со свежепрокаленным хлористым кальцием. Для дополнительной сушки воздуха в трубку 3 вводят 2 капли химически чистой серной кислоты ( уд.
 [3]

В трубку 3 вводят такой объем сухого воздуха, чтобы при температуре и барометрическом давлении, отвечающими времени установки нитрометра, он равнялся после отнесения к нормальным условиям ( к 0 и 760 мм давления) объему в 100 мл. Для этого, открыв кран / /, соединяют трубку 3 с воздухом через колонку со свежепрокаленным хлористым кальцием. Для дополнительной сушки воздуха в трубку 5 вводят 2 капли химически чистой серной кислоты ( уд.
 [4]

Вначале пустой цилиндр со снятыми штуцерами продувают 20-кратным объемом сухого воздуха ( влажность – 50 С по точке росы), после чего нижнюю горловину цилиндра закрывают накид – S гайкой с – медной прокладкой.
 [6]

Капля ртути запирает в капилляре с запаянным концом объем сухого воздуха. При измерении необходимо погружать в среду весь термометр. Перемещение капли ртути в капилляре показывает изменение объема газа; на капилляре нанесена шкала с отметками 0 и 100 для точек таяния льда и кипения воды, как и у ртутного термометра.
 [7]

Отношение веса определенного объема сухого газа к весу такого же объема сухого воздуха при одинаковых условиях принимается за удельный вес газа.
 [8]

А потому при давлении Н, если пар насыщает пространство, объемы сухого воздуха и влажности, в нем заключающейся, относятся, как ( Н – /) /, где / выражает давление паров, находимое из таблиц.
 [9]

Легко видеть, что при одинаковых давлении и температуре объем влажного воздуха V больше объема Уг сухого воздуха.
 [10]

Относительный удельный вес газа d представляет собой отношение веса сухого газа к весу такого же объема сухого воздуха, взятых при одинаковых температуре и давлении. Эта величина не имеет размерности.
 [12]

С; б) при уменьшении объема во столько раз, во сколько уменьшается при таком охлаждении объем сухого воздуха.
 [13]

Объем воздуха, прошедшего через сатуратор, v находится по количеству вытекшей воды с учетом того, что объем сухого воздуха, поступившего из системы в бутыли, меньше объема вытекшей воды, так как часть объема, освободившегося в результате вытеснения воды, занимается насыщенными парами воды.
 [14]

Теоретическая температура горения, подсчитанная с учетом диссоциации в условиях высокой температуры СОаиШО, равна 1950 при сжигании газа в стехиометрическом объеме сухого воздуха и при исходной температуре газа и воздуха – 0 С.
 [15]

Страницы:  

   1

   2

Уравнение состояния влажного воздуха

Влажный воздух представляет собой механическую смесь сухого воздуха и водяного пара. Поскольку критическая температура водя­ного пара (Т_кр =374 °С) выше наблюдаемых в атмосфере темпера­тур, то он в реальных условиях атмосферы может переходить в жид­кое и твердое состояния (конденсироваться).

Теория фазовых переходов водяного пара детально рассматрива­ется в разделе IV. Здесь отметим только, что условие Т

Примем следующие обозначения: р — общее давление; Т — тем­пература, одинаковая для водяного пара, сухого и влажного возду­ха; е — парциальное давление водяного пара; (р – е) — парциальное давление сухого воздуха. Уравнением состояния водяного пара слу­жит уравнение (1.4.1). Уравнение состояния сухой части воздуха имеет вид

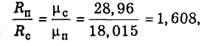
Подставим в уравнения (1.4.1) и (1.4.3) значения удельных объе­мов в соответствии с (1.4.2) и удельной газовой постоянной водяного пара в соответствии с (1.4.4):

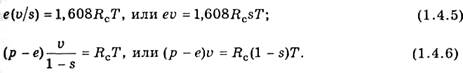
Сложив уравнения (1.4.5) и (1.4.6), получим уравнение состоя­ния влажного воздуха:

которому можно придать два различных вида в зависимости от того, отнесен ли множитель (1 + 0,608s) к удельной газовой постоянной Rc или к температуре Т.

Если ввести удельную газовую постоянную влажного воздуха

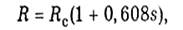
то уравнение (1.4.7) примет вид

Удельная газовая постоянная R в этом уравнении — величина переменная, зависящая от влажности воздуха s.

В метеорологии множитель (1 + 0,608s) обычно относят к темпе­ратуре, вводя понятие виртуальной температуры

Нередко виртуальную температуру представляют в виде суммы:

где ∆T_v — виртуальный добавок. Из сравнения последнего выраже­ния с (1.4.9) следует:

Если водяной пар находится в состоянии насыщения, то ∆T_v при данных Т и р достигает наибольшего значения

которое при фиксированном р является функцией одной лишь тем­пературы. При р = 1000 гПа максимальный виртуальный добавок ∆T_vт имеет следующие значения:

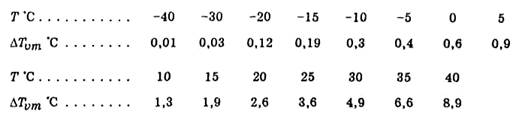
Из этих данных вытекает, что виртуальный добавок, а соответствен­но и роль влажности в изменении плотности воздуха малы при низ­ких температурах и достаточно велики при высоких.

С введением виртуальной температуры уравнение состояния влажного воздуха принимает вид

Если в (1.4.11) ввести плотность влажного воздуха p = l/v, то уравнение состояния влажного воздуха примет вид

Из сравнения уравнения (1.4.12) с уравнением (1.3.8) следует, что при одинаковых температуре и давлении плотность влажного воздуха всегда меньше плотности сухого воздуха. Физически это объясняется тем, что в состав влажного воздуха входит более лег­кий по сравнению с сухим воздухом водяной пар, который вытес­няет часть сухого воздуха.

Парциальное давление сухого воздуха и водяного пара

Плотность пара יS_m представляет собой отношение массы пара m_п (в килограммах) к объему V (в кубических метрах), занятому этим паром (такой же объем занимает и влажный воздух):

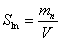
Удельный объем влажного воздуха

Представляет собой соотношение объема влажного воздуха к суммарной массе сухого воздуха и пара, входящих в данный объем, т.е.:

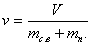
м 3 /кг влажного воздуха (3. 1.2.)

Уравнение состояния влажного воздуха

Для влажного воздуха, а так же его составных частей (сухого воздуха и перегретого водяного пара, содержащегося во влажном воздухе), применимо уравнение состояния идеального газа – уравнение Клайперона:

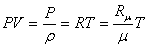
• Где P – давление газа (воздуха, пара), Па; ρ- 1/V– плотность газа, кг/м 3 ;
• T – абсолютная температура Кельвина, К;
• R — газовая постоянная, Дж/ (кгּК);
• μ- массовая масса, кг/моль;
• R_μ – универсальная газовая постоянная, равная 3,314 Дж/ (мольּК).

Для влажного воздуха справедлив так же объединенный закон Бойля-Мариотта и Гей-Люссака:

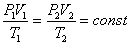
Формула (3. 1.4), где индексы 1 и 2 относятся, соответственно к одному и другому состоянию газа.

Воздух и атмосфера

Состав сухого воздуха у земной поверхности

Атмосфера состоит из смеси газов, называемой воздухом, в которой находятся во взвешенном состоянии жидкие и твердые частички. Общая масса последних незначительна в сравнении со всей массой атмосферы.

Атмосферный воздух у земной поверхности, как правило, является влажным. Это значит, что в его состав, вместе с другими газами, входит водяной пар, т.е. вода в газообразном состоянии. Содержание водяного пара в воздухе меняется в значительных пределах, в отличие от других составных частей воздуха: у земной поверхности оно колеблется между сотыми долями процента и несколькими процентами. Это объясняется тем, что при существующих в атмосфере условиях водяной пар может переходить в жидкое и твердое состояние и, наоборот, может поступать в атмосферу заново вследствие испарения с земной поверхности.

Воздух без водяного пара называют сухим воздухом. У земной поверхности сухой воздух на 99% состоит из азота (78% по объему или 76% по массе) и кислорода (21% по объему или 23% по массе). Оба эти газа входят в состав воздуха у земной поверхности в виде двухатомных молекул (N₂ и О₂).

Оставшийся 1% приходится почти целиком на аргон (Аr). Всего 0,08% остается на углекислый газ (СО₂). Многочисленные другие газы входят в состав воздуха в тысячных, миллионных и еще меньших долях процента. Это криптон, ксенон, неон, гелий, водород, озон, йод, радон, метан, аммиак, перекись водорода, закись азота и др.

Все перечисленные выше газы всегда сохраняют газообразное состояние при наблюдающихся в атмосфере температурах и давлениях не только у земной поверхности, но и в высоких слоях.

Процентный состав сухого воздуха у земной поверхности очень постоянен и практически одинаков повсюду. Существенно меняться может только содержание углекислого газа. В результате процессов дыхания и горения его объемное содержание в воздухе закрытых, плохо вентилируемых помещений, а также промышленных центров может возрастать в несколько раз — до 0,1—0,2%. Совершенно незначительно меняется процентное содержание азота и кислорода.

Водяной пар в воздухе

Процентное содержание водяного пара во влажном воздухе у земной поверхности составляет в среднем от 0,2% в полярных широтах до 2,5% у экватора, а в отдельных случаях колеблется почти от нуля до 4%. В связи с этим становится переменным и процентное соотношение других газов во влажном воздухе. Чем больше в воздухе водяного пара, тем меньшая часть его объема приходится на постоянные газы при тех же условиях давления и температуры.

Водяной пар непрерывно поступает в атмосферу путем испарения с водных поверхностей, с влажной почвы и путем транспирации растений, при этом в разных местах и в разное время он поступает в различных количествах. От земной поверхности он распространяется вверх, а воздушными течениями переносится из одних мест Земли в другие.

В атмосфере может возникать состояние насыщения. В таком состоянии водяной пар содержится в воздухе в количестве, предельно возможном при данной температуре. Водяной пар при этом называют насыщающим, а воздух, содержащий его, насыщенным.

Состояние насыщения обычно достигается при понижении температуры воздуха. Когда это состояние достигнуто, то при дальнейшем понижении температуры часть водяного пара становится избыточной и конденсируется, переходит в жидкое или твердое состояние. В воздухе возникают водяные капельки и ледяные кристаллики облаков и туманов. Облака могут снова испаряться; в других случаях капельки и кристаллики облаков, укрупняясь, могут выпадать на земную поверхность в виде осадков. Вследствие всего этого содержание водяного пара в каждом участке атмосферы непрерывно меняется.

С водяным паром в воздухе и с его переходами из газообразного состояния в жидкое и твердое связаны важнейшие процессы погоды и особенности климата. Наличие водяного пара в атмосфере существенно сказывается на тепловых условиях атмосферы и земной поверхности. Водяной пар сильно поглощает длинноволновую инфракрасную радиацию, которую излучает земная поверхность. В свою очередь и сам он излучает инфракрасную радиацию, большая часть которой идет к земной поверхности. Это уменьшает ночное охлаждение земной поверхности и тем самым также нижних слоев воздуха. На испарение воды с земной поверхности затрачиваются большие количества тепла, а при конденсации водяного пара в атмосфере это тепло отдается воздуху. Облака, возникающие в результате конденсации, отражают и поглощают солнечную радиацию на ее пути к земной поверхности. Осадки, выпадающие из облаков, являются важнейшим элементом погоды и климата. Наконец, наличие водяного пара в атмосфере имеет важное значение для физиологических процессов.

Упругость водяного пара и относительная влажность

Содержание водяного пара в воздухе называют влажностью воздуха. Основные характеристики влажности – это упругость водяного пара и относительная влажность. Абсолютная влажность воздуха – количество водяного пара в единице объема (г/м 3 ).

Водяной пар, как всякий газ, обладает упругостью (давлением). Упругость водяного пара е пропорциональна его плотности (содержанию в единице объема) и его абсолютной температуре. Она выражается в тех же единицах, что и давление воздуха, т. е. либо в миллиметрах ртутного столба, либо в миллибарах.

Упругость водяного пара в состоянии насыщения называют упругостью насыщения. Это максимальная упругость водяного пара, возможная при данной температуре. Например, при температуре 0° упругость насыщения равна 6,1 мб. На каждые 10° температуры упругость насыщения увеличивается примерно вдвое.

Если воздух содержит водяного пара меньше, чем нужно для насыщения его при данной температуре, можно определить, насколько воздух близок к состоянию насыщения. Для этого вычисляют относительную влажность. Так называют отношение фактической упругости е водяного пара, находящегося в воздухе, к упругости насыщения Е при той же температуре, выраженное в процентах, т. е. r = e/E * 100%

Например, при температуре 20° упругость насыщения равна 23,4 мб. Если при этом фактическая упругость пара в воздухе будет 11,7 мб, то относительная влажность воздуха равна (11,7/23,4)*100 = 50%. Упругость водяного пара у земной поверхности меняется от сотых долей миллибара (при очень низких температурах зимой в Антарктиде и в Якутии) до 35 мб и более (у экватора). Чем теплее воздух, тем больше водяного пара может он содержать без насыщения и, стало быть, тем больше может быть в нем упругость водяного пара.

Относительная влажность воздуха может принимать все значения от нуля для вполне сухого воздуха (е = 0) до 100% для состояния насыщения (е=Е).

Изменение состава воздуха с высотой

Процентное содержание составных частей сухого воздуха в нескольких нижних десятках километров (до 100-120 км) с высотой почти не меняется. Воздух, находящийся в постоянном движении, хорошо перемешивается по вертикали, и атмосферные газы не расслаиваются по плотности, как это было бы в условиях спокойной атмосферы (где доля более легких газов должна была бы возрастать с высотой).

Однако выше 100 км такое расслоение газов по плотности начинается и постепенно увеличивается с высотой. Примерно до высоты 200 км преобладающим газом атмосферы все-таки остается азот. Выше начинает преобладать кислород, причем кислород в атомарном состоянии: под действием ультрафиолетовой радиации Солнца его двухатомные молекулы разлагаются на заряженные атомы. Выше 1000 км атмосфера состоит главным образом из гелия и водорода, причем водород – также в атомарном состоянии, т. е. в виде заряженных атомов, – преобладает.

Процентное содержание водяного пара в воздухе меняется с высотой. Водяной пар постоянно поступает в атмосферу снизу, а распространяясь вверх конденсируется, сгущается. Поэтому упругость и плотность водяного пара убывают с высотой быстрее, чем упругость и плотность остальных газов воздуха.

На высоте 5 км упругость водяного пара и, следовательно, его содержание в воздухе в десять раз меньше, чем у земной поверхности, а на высоте 8 км – в сто раз меньше. Таким образом, выше 10-15 км содержание водяного пара в воздухе ничтожно мало.

Распределение озона в атмосфере

Изменение с высотой содержания озона в воздухе особенно интересно. У земной поверхности озон содержится в ничтожных количествах. С высотой содержание его возрастает, причем не только в процентном отношении, но и по абсолютным значениям. Максимальное содержание озона наблюдается на высотах 25-30 км; выше оно убывает и на высотах около 60 км сходит на нет.

Процесс образования озона из кислорода происходит в слоях от 60 до 15 км при поглощении кислородом ультрафиолетовой солнечной радиации. Часть двухатомных молекул кислорода разлагается на атомы, а атомы присоединяются к сохранившимся молекулам, образуя трехатомные молекулы озона. Одновременно происходит обратный процесс превращения озона в кислород. В слои ниже 15 км озон заносится из вышележащих слоев при перемешивании воздуха.

Если бы можно было сосредоточить весь атмосферный озон под нормальным давлением, он образовал бы слой только около 3 мм толщиной (приведенная толщина слоя озона). Но и в таком ничтожном количестве озон важен потому, что, сильно поглощая солнечную радиацию, он повышает температуру тех слоев атмосферы, в которых он находится. Ультрафиолетовую радиацию Солнца с длинами волн от 0,15 до 0,29 мк (один микрон – тысячная доля миллиметра) он поглощает целиком. Эта радиация производит физиологически вредное действие, и озон, поглощая ее, предохраняет от нее живые организмы на земной поверхности.

Жидкие и твердые примеси к атмосферному воздуху

Кроме перечисленных выше атмосферных газов, в воздух местами могут проникать другие газы, особенно соединения, возникающие при сгорании топлива (окислы серы, углерода, фосфора и др.). Наиболее заражается такими примесями воздух больших городов и промышленных районов.

В состав атмосферы входят также твердые и жидкие частички, взвешенные в атмосферном воздухе. Кроме водяных капелек и кристаллов, возникающих в атмосфере при конденсации водяного пара, это пыль почвенного и органического происхождения; твердые частички дыма, сажи, пепла и капельки кислот, попадающие в воздух при лесных пожарах, при сжигании топлива, при вулканических извержениях; частички морской соли, попадающие в воздух при разбрызгивании морской воды во время волнения; микроорганизмы (бактерии); пыльца, споры; наконец, космическая пыль, попадающая в атмосферу (около миллиона тонн в год) из межпланетного пространства, а также возникающая при сгорании метеоров в атмосфере. Особое место среди атмосферных примесей занимают продукты искусственного радиоактивного распада, заражающие воздух при испытательных взрывах атомных и термоядерных бомб.

Небольшую часть перечисленных примесей составляет крупная пыль, с частичками радиусом более 5 мк. Почти 95% частичек имеет радиусы менее 5 мк. Вследствие такой малости они могут длительное время удерживаться в атмосфере во взвешенном состоянии. Удаляются из атмосферы они главным образом при выпадении осадков, присоединяясь к капелькам и снежинкам.

Все эти так называемые, аэрозольные примеси, или аэрозоли, в наибольшем количестве содержатся в самых нижних слоях атмосферы: ведь основной их источник – земная поверхность. Особенно загрязнен ими воздух больших городов. Не говоря о вредных газовых примесях (SO₂, CO и др.), на каждый кубический сантиметр воздуха здесь приходятся десятки тысяч аэрозольных частичек, а за год на каждый квадратный километр выпадают из атмосферы сотни тонн аэрозолей. В сельских местностях количество частичек аэрозольных примесей в приземном воздухе исчисляется только тысячами на кубический сантиметр, а над океаном – только сотнями.

С высотой число взвешенных частичек быстро убывает; на высотах 5-10 км их всего десятки на кубический сантиметр.

В общем, в атмосферном столбе над каждым квадратным сантиметром земной поверхности содержится 10 8 -10 9 аэрозольных частичек. Общий их вес в атмосфере не менее 10 8 т. Это огромное число; но оно мало по сравнению со всей массой атмосферы, которая, как мы увидим дальше, определяется в 5*10 15 т.

Бактерии в центральных частях океанов встречаются в количестве нескольких единиц на кубический метр воздуха; в больших городах их уже тысячи и десятки тысяч в том же объеме.

От количества и рода аэрозольных примесей зависят явления поглощения и рассеяния радиации в атмосфере, т. е. ее большая или меньшая прозрачность для радиации. Наличие взвешенных частичек создает в атмосфере также ряд оптических явлений, свойственных коллоидным растворам.

Наиболее крупные аэрозольные частички, обладающие гигроскопическими свойствами, играют в атмосфере роль ядер конденсации, т. е. центров, к которым присоединяются молекулы водяного пара, образуя водяные капельки.

Аэрозольные примеси к воздуху могут легко переноситься воздушными течениями на большие расстояния. Песчаная пыль, попадающая в воздух над пустынями Африки и Передней Азии, неоднократно выпадала в больших количествах на территории Южной и Средней Европы. Дым и пепел больших вулканических извержений неоднократно распространялись в высоких слоях атмосферы на огромные расстояния, окутывая весь Земной шар. Помутнение воздуха и аномально красная окраска зорь наблюдались в течение многих месяцев после извержений.

Дымка, облака, туманы

Капельки и кристаллы, в отличие от пылинок, возникают в самой атмосфере при конденсации водяного пара и могут исчезать, не выпадая, вследствие испарения. Если они очень разрежены и мелки, то обнаруживаются по некоторому помутнению воздуха синеватого или сероватого цвета – дымке. Более плотные их скопления – облака и туманы.

Капельки облаков обычно очень мелки – от единиц до десятков микронов в диаметре. В каждом кубическом сантиметре облачного воздуха содержится несколько десятков или сотен капелек. Это значит, что на один кубический метр облачного воздуха приходится всего несколько граммов или даже долей грамма жидкой воды. Кристаллики в облаках также в большинстве очень мелки. Поэтому облака могут длительно удерживаться в атмосфере во взвешенном состоянии вследствие сопротивления воздуха и его восходящих движений. Но в облаках может происходить и укрупнение облачных элементов; достигнув определенных размеров, они начинают выпадать из облаков в виде осадков – капелек дождя, кристаллов снега и пр.

Нередко облакоподобные скопления капелек и кристаллов начинаются от самой земной поверхности; в этих случаях они называются туманами.

Ионы в атмосфере

Часть молекул атмосферных газов и частиц атмосферного аэрозоля – капелек, пылинок, кристаллов – несет электрические заряды. Эти заряженные частички называются ионами.

Молекулы воздуха заряжаются вследствие потери электрона или присоединения свободного электрона. К заряженной молекуле присоединяются другие молекулы, в которых происходит путем индукции разделение зарядов. Так возникает электрически заряженный комплекс молекул, называемый легким ионом. Заряженные молекулы могут также присоединяться к ядрам конденсации или пылинкам, взвешенным в воздухе, вследствие чего возникают более крупные тяжелые ионы с массами в тысячи раз большими, чем у легких ионов.

Капельки и кристаллы облаков и осадков, возникая на ионах как на ядрах конденсации, присоединяя их в дальнейшем, а также, получая электрические заряды другими способами, также могут стать носителями электрических зарядов. Заряды капелек и кристаллов гораздо больше, чем заряды ионов: они могут достигать многих миллионов элементарных зарядов (зарядов электрона).

С высотою содержание ионов увеличивается, особенно в слоях выше 80-100 км. Как говорилось выше, ионы являются здесь в основном заряженными атомами кислорода, гелия и водорода и окиси азота. Кроме того, значительная часть ионов в высоких слоях представляет собой свободные электроны.

Так же как и незаряженные частички, ионы в атмосфере постоянно перемещаются. Именно благодаря этому атмосфера обладает электропроводностью, в нижних слоях малой, в высших – значительной.

Электрическое поле атмосферы

Итак, в атмосфере всегда существуют подвижные электрические заряды, связанные с ионами, а также с элементами облаков и осадков. Заряды эти – обоих знаков, причем преобладают положительные, так что суммарный заряд атмосферы – положительный. При этом с высотой он растет. Сама земная поверхность также обладает электрическим зарядом, притом в сумме отрицательным (порядка -6*10 5 кулонов).

В грозовых облаках происходит сильная электризация облачных элементов и разделение положительных и отрицательных зарядов по отдельным частям облака. Вследствие этого в облаках, а также между облаками и землей возникают огромные разности потенциалов, при которых напряженность поля доходит до десятков тысяч вольт на метр. При этом в атмосфере возникают не только положительные, но и отрицательные заряды, индуцирующие положительный заряд на земной поверхности. В связи с указанными огромными разностями потенциалов в атмосфере возникают искровые электрические разряды, молнии, как в облаках, так и между облаками и землей. При напряженности поля, направленной вверх, молнии могут переносить к земной поверхности очень большие отрицательные заряды, которые и компенсируют потерю отрицательного заряда земной поверхностью в спокойную погоду.

Уравнение состояния газов

Основными характеристиками физического состояния газа являются его давление, температура и плотность. Эти три характеристики не независимы одна от другой. Газы сжимаемы; поэтому плотность их меняется в широких пределах в зависимости от давления и, кроме того, зависит от температуры. Связь между давлением, температурой и плотностью для идеальных газов дается уравнением состояния газов, известным из физики. Оно пишется

Уравнение состояния газов с достаточным приближением применимо и к сухому воздуху, и к водяному пару, и к влажному воздуху. В каждом случае будет своя величина газовой постоянной R. Для влажного воздуха R меняется в зависимости от упругости водяного пара, содержащегося в воздухе.

Атмосферное давление

Всякий газ производит давление на ограничивающие его стенки, т. е. действует на эти стенки с какой-то силой давления, направленной перпендикулярно (нормально) к стенке. Числовую величину этой силы давления, отнесенную к единице площади, и называют давлением. Давление газа объясняется движениями его молекул, той “бомбардировкой”, которой они подвергают стенки. При возрастании температуры и при сохранении объема газа скорости молекулярных движений увеличиваются и, следовательно, давление растет.

В каждой точке атмосферы имеется определенная величина атмосферного давления, или давления воздуха.

Атмосферное давление можно выразить, например, в граммах или килограммах веса на один квадратный сантиметр или метр. На уровне моря оно близко к одному килограмму на квадратный сантиметр. В метеорологии его выражают, однако, в других единицах.

С давних пор принято выражать атмосферное давление в миллиметрах ртутного столба. Это значит, что давление атмосферы сравнивают с эквивалентным ему давлением столба ртути. Когда говорят, например, что атмосферное давление на земной поверхности в данном месте равно 750 мм, это значит, что столб ртути высотою 750 мм давил бы на земную поверхность так же, как давит воздух.

Выражение давления в миллиметрах ртутного столба появилось в метеорологии не случайно. Оно связано с устройством основного прибора для измерения атмосферного давления – ртутного барометра. В этом приборе, известном из элементарного курса физики, атмосферное давление как раз уравновешивается давлением столба ртути; по изменениям высоты ртутного столба можно судить об изменениях атмосферного давления. На уровне моря среднее атмосферное давление близко к 760 мм рт. ст.

В отдельных случаях давление может меняться на уровне моря в пределах 150 мм рт. ст. С высотой атмосферное давление быстро убывает.

В настоящее время в метеорологии давление выражают в абсолютных единицах – миллибарах (мб). Один миллибар есть давление, которое сила в 1000 дин производит на площадь в один квадратный сантиметр. Среднее атмосферное давление на уровне моря – 760 мм рт. ст. – близко к 1013 мб, а 750 мм рт. ст. эквивалентны 1000 мб. Таким образом, для перехода от величины давления в миллиметрах ртутного столба к величине в миллибарах нужно давление в миллиметрах ртутного столба умножить на 4/3.

Температура воздуха

Воздух, как и всякое тело, всегда имеет температуру, отличную от абсолютного нуля. У земной поверхности температура воздуха варьирует в довольно широких пределах: крайние ее значения, наблюдавшиеся до сих пор, немного ниже +60° (в тропических пустынях) и около -90° (на материке Антарктиды).

С высотою температура воздуха меняется в разных слоях и в разных случаях по-разному. В среднем она сначала понижается до высоты 10-15 км, затем растет до 50-60 км, потом снова падает и т. д.

Температура воздуха, а также почвы и воды в большинстве стран выражается в градусах международной температурной шкалы, или шкалы Цельсия (°С), общепринятой в физических измерениях. Нуль этой шкалы приходится на температуру, при которой тает лед, а +100° – на температуру кипения воды (то и другое при давлении 760 мм рт. ст., близком к фактически существующим на уровне моря условиям). Однако в США и во многих странах Содружества наций употребительна шкала Фаренгейта (F). В этой шкале интервал между точками таяния льда и кипения воды разделен на 180°, причем точке таяния льда приписано значение +32°. Нуль шкалы Цельсия соответствует +32°F, a +100°C = +212°F.

Кроме того, в теоретической метеорологии применяется абсолютная шкала температуры (шкала Кельвина, К).

Плотность воздуха

Плотность воздуха непосредственно не измеряется: она вычисляется с помощью уравнения состояния газов. Применяя уравнение состояния газов к сухому воздуху, следует ввести числовое значение газовой постоянной для сухого воздуха R_d, равное 2,87*10 6 , если ρ и р взяты в системе единиц CGS (давление в дин/см 2 и плотность в г/см 3 ).

Найдем теперь выражение для плотности влажного воздуха с температурой Т, давлением р и упругостью водяного пара е. Можно представлять влажный воздух как смесь сухого воздуха и водяного пара. Из общего давления воздуха р на долю сухого воздуха приходится давление р – e. Следовательно, для этой части смеси, для сухого воздуха, уравнение состояния напишется так:

Влажный воздух несколько менее плотен, чем сухой воздух при тех же значениях давления и температуры. Это объясняется тем, что водяной пар менее плотен, чем сухой воздух.

Плотность воздуха в каждом месте непрерывно меняется во времени. Кроме того, она сильно меняется с высотой, потому что с высотой меняются также атмосферное давление и температура воздуха. Давление с высотой всегда уменьшается, а вместе с ним убывает и плотность. Температура с высотой по большей части понижается, по крайней мере в нижних 10-15 км атмосферы. Но падение температуры влечет за собой повышение плотности. В результате совместного влияния изменения давления и температуры плотность с высотой, как правило, понижается, но не так сильно, как давление. В среднем для Европы она равна у земной поверхности 1250 г/м 3 , на высоте 5 км – 735 г/м 3 , 10 км – 411 г/м 3 , 20 км – 87 г/м 3 .

Если бы плотность воздуха не менялась с высотой, а оставалась на всех уровнях такой же, как у земной поверхности, то высота атмосферы получилась бы около 8000 м. Указанная высота (8000 м) называется высотой однородной атмосферы. В действительности плотность воздуха с высотой убывает, и потому истинная высота атмосферы равняется многим тысячам километров.

Основное уравнение статики атмосферы

Теперь поставим вопрос: по какому закону меняется атмосферное давление с высотой?

Возьмем вертикальный столб воздуха с поперечным сечением, равным единице, и выделим в этом столбе бесконечно тонкий слой, ограниченный снизу поверхностью на высоте z, а сверху – поверхностью на высоте z + dz; толщина слоя, таким образом, dz. На нижнюю поверхность выделенного элементарного объема смежный воздух действует с силой давления, направленной снизу вверх; величина этой силы на рассматриваемую поверхность с площадью, равной единице, и будет давлением воздуха р на этой поверхности. На верхнюю поверхность элементарного объема смежный воздух действует с силой давления, направленной сверху вниз. Числовая величина этой силы p + dp есть давление на верхней границе.

Кроме того, воздух в рассматриваемом элементарном объеме испытывает силу тяжести, которая направлена вниз и равна ускорению силы тяжести g (ускорению свободно падающего тела), умноженному на массу воздуха во взятом объеме. Так как при поперечном сечении, равном единице, объем равен dz, то масса воздуха в нем равна ρdz, где ρ – плотность воздуха, а сила тяжести равна gρdz. Допустим, что в атмосфере существует равновесие также и в вертикальном направлении, т. е. что взятый объем воздуха не имеет никакого ускорения также и по вертикали и, таким образом, остается на одном и том же уровне, несмотря на наличие веса. Это значит, что сила тяжести (вес) и силы давления уравновешиваются. Вниз направлены сила давления p + dp и вес gρdz; возьмем их с отрицательным знаком. Вверх направлена сила давления р, которую возьмем с положительным знаком. Сумму всех этих трех сил приравняем нулю и, таким образом, получим dp = -gρdz. (1)

Отсюда следует, что при положительном dz имеем отрицательное dp, т. е. что с высотой атмосферное давление падает. При этом разность давлений на нижней и верхней границах рассматриваемого элементарного объема равна весу воздуха в этом объеме.

Уравнение (1) носит название основного уравнения статики атмосферы. Это дифференциальное уравнение говорит о том, как меняется давление при бесконечно малом приросте высоты.

Основное уравнение статики можно написать еще так: -(1/ρ)*(dp/dz) – g = 0

Величина -dp/dz падение давления на единицу прироста высоты, т. е. вертикальный барический градиент (вертикальный градиент давления). Это равнодействующая сил давления, направленных сверху и снизу на единицу нашего объема.

Разделив ее на плотность ρ, мы получим силу вертикального барического градиента, отнесенную к единице массы и направленную вверх.

Второй член – это сила тяжести, действующая на ту же единицу массы и направленная вниз. Она равна силе барического градиента, но направлена в противоположную сторону. Следовательно, основное уравнение статики выражает условие равновесия между двумя силами, действующими на единицу массы воздуха по вертикали, – силой вертикального барического градиента и силой тяжести.

Выше было показано, что бесконечно малая разность давлений равна весу элементарного объема воздуха с толщиной dz. Следовательно, и конечная разность давлений между нижним и верхним уровнем равна весу воздушного столба между этими уровнями. Если за верхний уровень принять верхнюю границу атмосферы, на которой давление практически равно нулю, то очевидно, что давление на любом уровне равно весу всего столба атмосферы, простирающегося над данным уровнем.

Применения барометрической формулы

С помощью барометрической формулы можно решить три задачи:

1) зная давление на одном уровне и среднюю температуру столба воздуха, найти давление на другом уровне;

2) зная давление на обоих уровнях и среднюю температуру столба воздуха, найти разность уровней (барометрическое нивелирование);

3) зная разность уровней и величины давления на них, найти среднюю температуру столба воздуха.

Важным вариантом первой задачи, поставленной выше, является приведение давления к уровню моря. Зная давление на некоторой станции, расположенной на высоте z над уровнем моря, и температуру t на этой станции, вычисляют сначала воображаемую среднюю температуру между рассматриваемой станцией и уровнем моря (в действительности атмосферного столба между станцией и уровнем моря не будет). Для уровня станции берется фактическая температура, а для уровня моря – та же температура, но увеличенная в той мере, в какой в среднем меняется температура воздуха с высотой.

Средний вертикальный градиент температуры в тропосфере принимается равным 0,6° на 100 м. Следовательно, если станция имеет высоту 200 м и температура на ней +16°, то для уровня моря принимается температура +17,2°, а средняя температура столба между станцией и уровнем моря +16,6°. После этого по давлению на станции и по полученной средней температуре определяется давление на уровне моря. Для этого составляют особые таблицы для каждой станции.

Приведение давления к уровню моря является очень важной операцией. На приземные синоптические карты всегда наносится давление, приведенное к уровню моря. Этим исключается влияние различий в высотах станций на величины давления и становится возможным выяснить горизонтальное распределение давления.

Среднее распределение атмосферного давления с высотой

Распределение атмосферного давления по высоте зависит от того, каково давление внизу и как распределяется температура воздуха с высотой. В многолетнем среднем для Европы давление на уровне моря равно 1014 мб, на высоте 5 км – 538 мб, 10 км – 262 мб, 15 км – 120 мб и 20 км – 56 мб. Эти значения подтверждают вывод, который можно сделать из барометрической формулы: давление убывает примерно в геометрической прогрессии, когда высота возрастает в арифметической прогрессии. На уровне 5 км давление почти вдвое ниже, чем на уровне моря, на уровне 10 км – почти в четыре раза, на уровне 15 км – почти в 8 раз и на уровне 20 км – в 18 раз. На высоте 100 км давление измеряется только долями миллибара.

Давление меняется не только с высотой. На одном и том же уровне оно не везде одинаково. Кроме того, в каждой точке атмосферы давление непрерывно меняется с течением времени; стало быть, непрерывно меняется и распределение его во всей атмосфере. Ясно, что изменения давления в любой точке связаны с изменениями всей массы воздуха над этой точкой. А изменения массы воздуха в свою очередь обусловлены движением воздуха.

Общая масса атмосферы

Знание атмосферного давления позволяет рассчитать общую массу атмосферы. Среднее атмосферное давление на уровне моря эквивалентно весу столба ртути высотой 760 мм. Масса ртутного столба высотой 760 мм над одним квадратным сантиметром земной поверхности составляет 1033,2 г. Таков же, очевидно, будет и средний вес столба атмосферы над одним квадратным сантиметром поверхности на уровне моря. Зная площадь земной поверхности и превышение материков над уровнем моря, можно вычислить общий вес всей атмосферы. Пренебрегая изменениями силы тяжести с высотой, можно считать этот вес численно равным массе атмосферы.

Общая масса атмосферы составляет немного больше 5*10 21 г, или 5*10 15 т. Это примерно в миллион раз меньше, чем масса самого Земного шара.

Адиабатические изменения состояния в атмосфере

Очень важную роль в атмосферных процессах играет то обстоятельство, что температура воздуха может изменяться и часто действительно изменяется адиабатически, т. е. без теплообмена с окружающей средой (с окружающей атмосферой, земной поверхностью и мировым пространством). Вполне строго адиабатических процессов в атмосфере не бывает: никакая масса воздуха не может быть полностью изолирована от теплового влияния окружающей среды. Однако если атмосферный процесс протекает быстро и теплообмен за это время мал, то изменение состояния можно с достаточным приближением считать адиабатическим.

Если некоторая масса воздуха в атмосфере адиабатически расширяется, то давление в ней падает, а вместе с ним падает и температура. Напротив, при адиабатическом сжатии массы воздуха давление и температура в ней растут. Эти изменения температуры, не связанные с теплообменом, происходят вследствие преобразования внутренней энергии газа (энергии положения и движения молекул) в работу или работы во внутреннюю энергию. При расширении массы воздуха производится работа против внешних сил давления, так называемая работа расширения, на которую затрачивается внутренняя энергия воздуха. Но внутренняя энергия газа пропорциональна его абсолютной температуре; поэтому температура воздуха при расширении падает. Напротив, при сжатии массы воздуха производится работа сжатия. Внутренняя энергия рассматриваемой массы воздуха вследствие этого возрастает, т. е. скорость молекулярных движений увеличивается. Следовательно, растет и температура воздуха.

Сухоадиабатические изменения температуры при вертикальных движениях

В атмосфере расширение воздуха и связанное с ним падение давления и температуры происходят в наибольшей степени при восходящем движении воздуха. Такой подъем воздуха может происходить разными способами: в виде восходящих токов конвекции; над поверхностью фронта – при движении обширных слоев воздушной массы вверх по пологому клину другой, более холодной воздушной массы; при подъеме воздуха по горному склону. Аналогичным образом сжатие воздуха, сопровождающееся повышением давления и температуры, происходит при опускании, при нисходящем движении воздуха. Отсюда важный вывод: восходящий воздух адиабатически охлаждается, нисходящий воздух адиабатически нагревается.

Нетрудно подсчитать, на сколько метров должен подняться или опуститься воздух, чтобы температура в нем понизилась или повысилась на один градус. При адиабатическом подъеме сухого или ненасыщенного воздуха температура на каждые 100 м подъема падает почти точно на один градус, а при адиабатическом опускании на 100 м температура растет на ту же величину. Эта величина 1°/100 м называется сухоадиабатическим градиентом. Еще раз напомним, что речь идет об изменении температуры с высотой в вертикально движущейся индивидуальной частице воздуха. Не следует смешивать термин “градиент” в этом значении с вертикальным градиентом.

Влажноадиабатические изменения температуры

С адиабатическим подъемом влажного ненасыщенного воздуха связано такое важное изменение, как приближение его к состоянию насыщения. Температура воздуха при его подъеме понижается; поэтому на какой-то высоте достигается насыщение. Эта высота называется уровнем конденсации.

При дальнейшем подъеме влажный насыщенный воздух охлаждается иначе, чем ненасыщенный. В нем происходит конденсация, а при конденсации выделяется в значительных количествах скрытая теплота парообразования, или теплота. Выделение этой теплоты замедляет понижение температуры воздуха при подъеме. Поэтому в поднимающемся насыщенном воздухе температура падает уже не по уравнению Пуассона, а по влажноадиабатическому закону. Она падает тем медленнее, чем больше влагосодержание воздуха в состоянии насыщения (что в свою очередь зависит от температуры и давления). На каждые 100 м подъема насыщенный воздух при давлении 1000 мб и температуре 0° охлаждается на 0,66 , при температуре +20° – на 0,44° и при температуре -20° – на 0,88°. При более низком давлении падение температуры соответственно меньше. Падение температуры в насыщенном воздухе при подъеме его на единицу высоты (100 м) называют влажноадиабатическим градиентом.

При очень низких температурах, которые получает воздух при подъеме в высокие слои атмосферы, водяного пара в нем остается немного и выделение теплоты конденсации поэтому также мало. Падение температуры при подъеме в таком воздухе приближается к падению в сухом воздухе. Иначе говоря, влажноадиабатический градиент при низких, температурах приближается по величине к сухоадиабатическому. При опускании насыщенного воздуха процесс может происходить по-разному в зависимости от того, содержит ли воздух жидкие продукты конденсации (капельки и кристаллы), или они уже целиком выпали из воздуха в виде осадков.

Если в воздухе нет продуктов конденсации, то воздух, как только температура в нем начнет при опускании расти, сразу станет ненасыщенным. Поэтому воздух, опускаясь, будет нагреваться по сухоадиабатическому закону, т. е. на 1°/100 м. Если же в воздухе есть капельки и кристаллы, то они при опускании и нагревании воздуха будут постепенно испаряться. При этом часть тепла воздушной массы перейдет в скрытую теплоту парообразования, и потому повышение температуры при опускании замедлится. В результате воздух останется насыщенным до тех пор, пока все продукты конденсации не перейдут в газообразное состояние. А температура в нем будет в это время повышаться по влажноадиабатическому закону: не на 1°/100 м, а на меньшую величину – именно на такую, на какую понизилась бы температура в восходящем насыщенном воздухе при тех же значениях температуры и давления.

Псевдоадиабатический процесс

Представим себе, что влажный ненасыщенный воздух сперва поднимается. Его температура при этом падает сначала по сухоадиабатическому закону; затем, после того как достигнут уровень конденсации, – по влажноадиабатическому закону. Допустим также, что вся вода, выделяющаяся при конденсации, сразу же выпадает из воздуха в виде осадков. Допустим затем, что, достигнув некоторой высоты, воздух начинает опускаться. Так как продуктов конденсации в нем нет, то он будет при этом нагреваться по сухоадиабатическому закону. Легко рассчитать, что на прежний уровень воздух придет с температурой более высокой, чем та, которая была в нем первоначально.

Рассматриваемая масса воздуха совершила необратимый процесс. Хотя она вернулась на прежний уровень, под прежнее давление, она не вернулась в исходное состояние: ее конечная температура оказалась выше, чем была начальная. Такой процесс называется псевдоадиабатическим.

Потенциальная температура

Пусть на какой-то высоте в атмосфере имеется воздух с давлением р и температурой Т. Если бы этот воздух сухоадиабатически опустился на уровень, где существует стандартное давление р0, то температура его тоже изменилась бы по уравнению Пуассона.

Назовем эту температуру, которую воздух получил бы при стандартном давлении (1000 мб), его потенциальной температурой. Фактическую температуру воздуха, в отличие от потенциальной, будем называть молекулярной температурой. Очевидно, что потенциальная температура равна молекулярной температуре при стандартном давлении.

Потенциальную температуру можно с достаточным приближением определить, если известно, на какой высоте воздух находится. Пусть, например, эта высота равна 3000 м. Допустим, что на уровне моря давление стандартное, т. е. равно 1000 мб. Тогда потенциальная температура воздуха, т. е. температура, с которой он пришел бы на уровень моря, равна его начальной температуре плюс 30°, так как на каждые 100 м спуска температура воздуха должна возрастать на один градус.

С помощью потенциальной температуры можно сравнивать тепловое состояние масс воздуха, находящихся на разных высотах над уровнем моря, т. е. при разных давлениях. Вычисляя потенциальную температуру этих масс, мы как бы опускаем их на один уровень.

При изменении состояния воздуха по сухоадиабатическому закону потенциальная температура воздуха не меняется. Только когда начинается конденсация и выделяется скрытая теплота, потенциальная температура возрастает.

Вертикальное распределение температуры

Выше было указано, как меняется температура в определенной массе воздуха, которая адиабатически поднимается или опускается. Ни в коем случае не следует смешивать эти индивидуальные изменения с вертикальным распределением температуры в атмосфере.

Температура в атмосферном столбе может распределяться по высоте различным образом. Это распределение не подчинено никакой простой закономерности. Представление о распределении температуры с высотой дает вертикальный градиент температуры -dT/dz, т. е. изменение температуры в атмосфере на единицу высоты, обычно на 100 м. Так как перед производной ставится знак минус, то в обычном случае падения температуры с высотой, градиент имеет положительную величину.

Вертикальный градиент температуры может меняться в довольно широких пределах. В нижних 10 км в умеренных широтах и в нижних 15 км в тропиках он в среднем равен 0,6°/100 м. В нижних сотнях метров над нагретой подстилающей поверхностью он может повышаться до 1°/100 м или немного больше. Бывают и такие случаи, когда температура воздуха с высотой не падает, а растет. Такое распределение температуры называют инверсией температуры, а вертикальный градиент температуры будет при этом, очевидно, отрицательным. Инверсии особенно часты по ночам в приземном слое, но встречаются на разных высотах и в свободной атмосфере. Если температура в воздушном слое не меняется с высотой, т. е. вертикальный градиент ее равен нулю, то такое состояние слоя называют изотермией.

Ветер и турбулентность

В зависимости от распределения атмосферного давления воздух постоянно перемещается в горизонтальном направлении. Это горизонтальное перемещение называется ветром. Скорость и направление ветра все время меняются. Средние скорости ветра у земной поверхности близки к 5-10 м/сек. Но иногда, в сильных атмосферных вихрях, скорости ветра у земной поверхности могут достигать и превышать 50 м/сек. В высоких слоях атмосферы, в так называемых струйных течениях, регулярно наблюдаются скорости ветра до 100 м/сек и более.

К горизонтальному переносу воздуха присоединяются и вертикальные составляющие. Они обычно малы по сравнению с горизонтальным переносом, порядка сантиметров или десятых долей сантиметра в секунду. Только в особых условиях, при так называемой конвекции, в небольших участках атмосферы вертикальные составляющие скорости движения воздуха могут достигать нескольких метров в секунду.

Ветер всегда обладает турбулентностью. Это значит, что отдельные количества воздуха в потоке ветра перемещаются не по параллельным путям. В воздухе возникают многочисленные беспорядочно движущиеся вихри и струи разных размеров.

Турбулентность возникает вследствие различия скоростей ветра в смежных слоях воздуха. Особенно велика она в нижних слоях атмосферы, где скорость ветра быстро растет с высотой. Отдельные количества воздуха поднимаются вверх, если их температура выше, а, стало быть, плотность меньше, чем температура и плотность окружающего воздуха. Напротив, количества воздуха более холодные и плотные, чем окружающий воздух, опускаются вниз. Такое перемешивание воздуха за счет различий плотности происходит тем интенсивнее, чем быстрее падает температура с высотой, т. е. чем больше вертикальный градиент температуры. Поэтому можно условно говорить о динамической турбулентности, возникающей независимо от температурных условий, и о термической турбулентности, определяемой температурными условиями.

С такой упорядоченной конвекцией связано образование мощных облаков вертикального развития – кучевых и кучево-дождевых (ливневых). Для возникновения конвекции такого рода необходимо, чтобы вертикальный градиент температуры был очень велик, а именно близок к 1°/100 м или еще больше, по крайней мере до того уровня, начиная с которого возникают облака.

Турбулентный обмен

Турбулентность, включая и упорядоченную конвекцию, приводит к сильному перемешиванию воздуха, особенно в вертикальном направлении. Перемешивание это в тысячи и десятки тысяч раз сильнее, чем могло бы происходить только молекулярным путем, вследствие молекулярной диффузии.

Перемешивание воздуха в процессе турбулентности – турбулентная диффузия – приводит к распространению в атмосфере тепла и влаги, в особенности к их обмену по вертикали.

В процессе вертикального турбулентного обмена каждая переносимая субстанция (примесь к воздуху или его свойство) распространяется в том направлении, в котором она убывает, т. е. в направлении своего вертикального градиента. Содержание водяного пара и пыли, как правило, убывает кверху. Поэтому турбулентный перенос этих субстанций обычно направлен вверх.

Более сложен вопрос о турбулентном переносе тепла. Вследствие сжимаемости воздуха и адиабатических изменений температуры при вертикальных движениях о направлении переноса тепла нельзя судить по направлению градиента молекулярной температуры. Сохраняющейся характеристикой состояния воздуха (при сухоадиабатическом процессе) является его потенциальная температура. Передача тепла вверх начинается при вертикальных градиентах температуры меньше 1°/100 м.

Конечно, в разное время дня и года и над разной земной поверхностью перенос тепла может происходить в разных направлениях. Но в общем итоге передача тепла от земной поверхности в атмосферу перевешивает.

[spoiler title=”источники:”]

http://abratsev.ru/atmosphere/air.html

[/spoiler]

72,6% бесплатных материалов

967 руб. средняя цена курсовой работы

352 руб. средняя цена домашнего задания

119 руб. средняя цена решённой задачи

161 руб. средняя цена лабораторной работы

174 руб. средняя цена реферата

178 руб. средняя цена доклада

1624 руб. средняя цена ВКР

665 руб. средняя цена диссертации

596 руб. средняя цена НИР

358 руб. средняя цена отчёта по практике

276 руб. средняя цена ответов (шпаргалок)

202 руб. средняя цена лекций

224 руб. средняя цена семинаров

280 руб. средняя цена рабочей тетради

188 руб. средняя цена презентации

67 руб. средняя цена перевода

143 руб. средняя цена изложения

150 руб. средняя цена сочинения

308 руб. средняя цена статьи

Гарантия возврата средств