Вычисление объёмов
Объём тела, ограниченного сверху и снизу поверхностями $mathbf { textit { z } } =mathbf { textit { f } } _ { 1 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $mathbf { textit { z } } =mathbf { textit { f } } _ { 2 } (mathbf { textit { x } } $,$mathbf { textit { y } } )$, $(x,y)in D$, с боков – цилиндрической поверхностью с образующими, параллельными оси $mathbf { textit { Oz } } $, равен $v=iintlimits_D { left[ { f_1 (x,y)-f_2 (x,y) }right]dxdy } $; эта формула очевидно следует из геометрического смысла двойного интеграла.
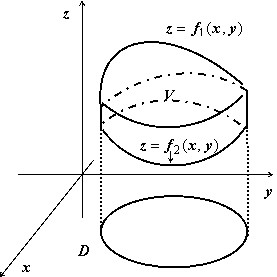
Основной вопрос, который надо решить – на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.
Пример 1
Найти объём тела $V:left[{ begin{array} { l } y=0,;z=0, \ x+y+z=4,; \ 2x+z=4. \ end{array} }right.$
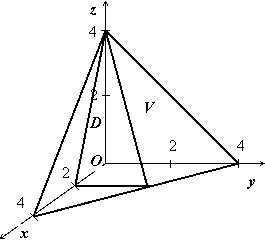
Решение:
Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $mathbf { textit { Oxz } } $:
$V:left[{ begin{array} { l } (x,z)in D, \ 0leqslant yleqslant 4-x-z. \ end{array} }right.$
Область $mathbf { textit { D } } $ – треугольник, ограниченный прямыми $mathbf { textit { x } } $ = 0, $mathbf { textit { z } } $ = 0, 2$mathbf { textit { x } } +mathbf { textit { z } } $ = 4, поэтому
$V=iintlimits_D { (4-x-z)dxdz } =intlimits_0^2 { dxintlimits_0^ { 4-2x } { (4-x-z)dz } } = intlimits_0^2 { dxleft. { left( { 4z-xz-z^2/2 }right) }right|_0^ { 4-2x } } = intlimits_0^2 { left[ { 16-8x-4x+2x^2-(4-2x)^2/2 }right]dx } = \ = intlimits_0^2 { left( { 8-4x }right)dx } = left. { left( { 8x-2x^2 }right) }right|_0^2 =16-8=8$
Пример 2
Найти объём области, ограниченной поверхностями $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } =mathbf { textit { R } } ^ { 2 } $,
$(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$.

Решение:
Первая поверхность – сфера, вторая – цилиндрическая – с образующими, параллельными оси $mathbf { textit { Oz } } $ { в уравнении нет $mathbf { textit { z } } $ в явной форме). Построить в плоскости $mathbf { textit { Oxy } } $ кривую шестого порядка, заданную уравнением $(mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )^ { 3 } =mathbf { textit { R } } ^ { 2 } (mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } )$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей { чётные степени } и точка $mathbf { textit { О } } (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(cos ^4varphi +sin ^4varphi );r^2=R^2((cos ^2varphi +sin ^2varphi )^2-2cos ^2varphi sin ^2varphi )=R^2(1-frac { sin ^22varphi } { 2 } )=$
$=R^2(1-frac { 1-cos 4varphi } { 4 } )=R^2frac { 3+cos 4varphi } { 4 } ;r=Rfrac { sqrt { 3+cos 4varphi } } { 2 } .$ Эту кривую построить уже можно. $r(varphi )$ максимально, когда $cos 4varphi =1;(varphi =0,frac { 2pi } { 4 } =frac { pi } { 2 } ,frac { 4pi } { 4 } =pi ,frac { 6pi } { 4 } =frac { 3pi } { 2 } )$, минимально, когда
$cos 4varphi =-1;(varphi =frac { pi } { 4 } ,frac { 3pi } { 4 } ,frac { 5pi } { 4 } ,frac { 7pi } { 4 } ),$ и гладко меняется между этими пределами { точка $mathbf { textit { О } } (0,0)$ не принадлежит этой кривой, где мы её потеряли? } .
Пользуясь симметрией, получаем $ V=16iintlimits_D { sqrt { R^2-x^2-y^2 } dxdy= } 16iintlimits_D { sqrt { R^2-r^2 } rdrdvarphi = } =16intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } rdr } = $ $ =-8intlimits_0^ { frac { pi } { 4 } } { dvarphi } intlimits_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } { sqrt { R^2-r^2 } d(R^2-r^2) } =-8frac { 2 } { 3 } intlimits_0^ { frac { pi } { 4 } } { left. { (R^2-r^2)^ { frac { 3 } { 2 } } }right|_0^ { Rfrac { sqrt { 3+cos 4varphi } } { 2 } } dvarphi } =-frac { 16 } { 3 } R^3intlimits_0^ { frac { pi } { 4 } } { left. { left[ { left( { frac { sin ^22varphi } { 2 } }right)^ { frac { 3 } { 2 } } -1 }right] }right|dvarphi } = $ и т.д.
Пример 3
Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)
Решение:
Данное тело показано на рисунке.
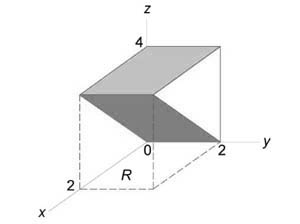
Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 – x.) Тогда объем равен $ { V = iintlimits_R { left[ { left( { 4 – x }right) – x }right]dxdy } } = { intlimits_0^2 { left[ { intlimits_0^2 { left( { 4 – 2x }right)dy } }right]dx } } = { intlimits_0^2 { left[ { left. { left( { 4y – 2xy }right) }right|_ { y = 0 } ^2 }right]dx } } = { intlimits_0^2 { left( { 8 – 4x }right)dx } } = { left. { left( { 8x – 2 { x^2 } }right) }right|_0^2 } = { 16 – 8 = 8. } $
Пример 4
Описать тело, объем которого определяется интегралом (V = intlimits_0^1 { dx } intlimits_0^ { 1 – x } { left( { { x^2 } + { y^2 } }right)dy } .)
Решение:
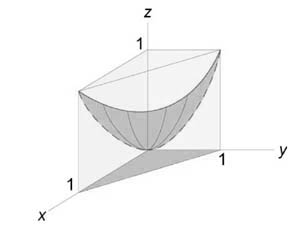
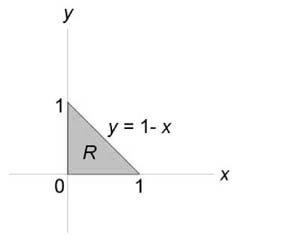
Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 – x) ниже параболической поверхности (z = { x^2 } + { y^2 } .) Объем тела равен $ { V = intlimits_0^1 { dx } intlimits_0^ { 1 – x } { left( { { x^2 } + { y^2 } }right)dy } } = { intlimits_0^1 { left[ { left. { left( { { x^2 } y + frac { { { y^3 } } } { 3 } }right) }right|_ { y = 0 } ^ { 1 – x } }right]dx } } = { intlimits_0^1 { left[ { { x^2 } left( { 1 – x }right) + frac { { { { left( { 1 – x }right) } ^3 } } } { 3 } }right]dx } } = \ = { intlimits_0^1 { left( { { x^2 } – { x^3 } + frac { { 1 – 3x + 3 { x^2 } – { x^3 } } } { 3 } }right)dx } } = { intlimits_0^1 { left( { 2 { x^2 } – frac { { 4 { x^3 } } } { 3 } – x + frac { 1 } { 3 } }right)dx } } = { left. { left( { frac { { 2 { x^3 } } } { 3 } – frac { 4 } { 3 } cdot frac { { { x^4 } } } { 4 } – frac { { { x^2 } } } { 2 } + frac { x } { 3 } }right) }right|_0^1 } = { frac { 2 } { 3 } – frac { 1 } { 3 } – frac { 1 } { 2 } + frac { 1 } { 3 } = frac { 1 } { 6 } . } $
Пример 5
Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)
Решение:
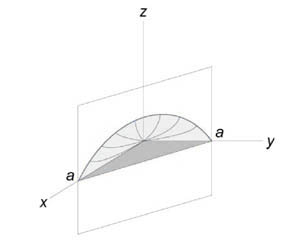
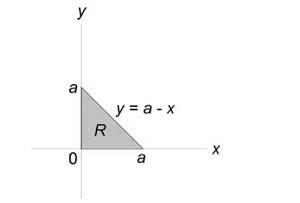
Данное тело лежит над треугольником (R) в плоскости (Oxy) ниже поверхности (z = xy.) Объем тела равен $ { V = iintlimits_R { xydxdy } } = { intlimits_0^a { left[ { intlimits_0^ { a – x } { xydy } }right]dx } } = { intlimits_0^a { left[ { left. { left( { frac { { x { y^2 } } } { 2 } }right) }right|_ { y = 0 } ^ { a – x } }right]dx } } = { frac { 1 } { 2 } intlimits_0^a { x { { left( { a – x }right) } ^2 } dx } } = { frac { 1 } { 2 } intlimits_0^a { xleft( { { a^2 } – 2ax + { x^2 } }right)dx } } = \ = { frac { 1 } { 2 } intlimits_0^a { left( { { a^2 } x – 2a { x^2 } + { x^3 } }right)dx } } = { frac { 1 } { 2 } left. { left( { { a^2 } cdot frac { { { x^2 } } } { 2 } – 2a cdot frac { { { x^3 } } } { 3 } + frac { { { x^4 } } } { 4 } }right) }right|_0^a } = { frac { 1 } { 2 } left( { frac { { { a^2 } } } { 2 } – frac { { 2 { a^4 } } } { 3 } + frac { { { a^4 } } } { 4 } }right) } = { frac { { { a^4 } } } { { 24 } } . } $
Пример 6
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( { x^2 } + { y^2 } = 1,) (z = 1 – x.)
Решение:
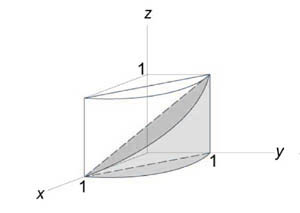
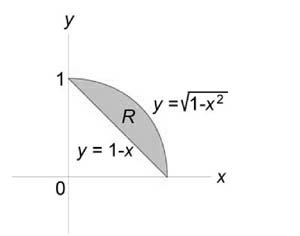
Как видно из рисунков, в области интегрирования (R) при (0 le x le 1) значения (y) изменяются от (1 – x) до (sqrt { 1 – { x^2 } } .)
Сверху тело ограничено плоскостью (z = 1 – x.) Следовательно, объем данного тела равен $ { V = iintlimits_R { left( { 1 – x }right)dxdy } } = { intlimits_0^1 { left[ { intlimits_ { 1 – x } ^ { sqrt { 1 – { x^2 } } } { left( { 1 – x }right)dy } }right]dx } } = { intlimits_0^1 { left[ { left( { 1 – x }right)left. y right|_ { 1 – x } ^ { sqrt { 1 – { x^2 } } } }right]dx } } = { intlimits_0^1 { left( { 1 – x }right)left( { sqrt { 1 – { x^2 } } – 1 + x }right)dx } } = \ = { intlimits_0^1 { left( { sqrt { 1 – { x^2 } } – xsqrt { 1 – { x^2 } } – 1 + 2x – { x^2 } }right)dx } } = { intlimits_0^1 { sqrt { 1 – { x^2 } } dx } } – { intlimits_0^1 { xsqrt { 1 – { x^2 } } dx } } – { intlimits_0^1 { left( { 1 + 2x – { x^2 } }right)dx } . } $
Вычислим полученные три интеграла отдельно. $ { I_1 } = intlimits_0^1 { sqrt { 1 – { x^2 } } dx } .$ Сделаем замену: (x = sin t.) Тогда (dx = cos tdt.) Видно, что (t = 0) при (x = 0) и (t = largefrac { pi } { 2 } normalsize) при (x = 1.) Следовательно, $ { { I_1 } = intlimits_0^1 { sqrt { 1 – { x^2 } } dx } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { sqrt { 1 – { { sin } ^2 } t } cos tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { { { cos } ^2 } tdt } } = { intlimits_0^ { largefrac { pi } { 2 } normalsize } { frac { { 1 + cos 2t } } { 2 } dt } } = { frac { 1 } { 2 } intlimits_0^ { largefrac { pi } { 2 } normalsize } { left( { 1 + cos 2t }right)dt } } = { frac { 1 } { 2 } left. { left( { t + frac { { sin 2t } } { 2 } }right) }right|_0^ { largefrac { pi } { 2 } normalsize } } = { frac { 1 } { 2 } left( { frac { pi } { 2 } + frac { { sin pi } } { 2 } }right) = frac { pi } { 4 } . } $ { Сравните с площадью сектора единичного круга в первом квадранте).
Вычислим второй интеграл ( { I_2 } = intlimits_0^1 { xsqrt { 1 – { x^2 } } dx } ,) используя замену переменной. Полагаем (1 – { x^2 } = w.) Тогда (-2xdx = dw) или (xdx = largefrac { { – dw } } { 2 } normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ { { I_2 } = intlimits_0^1 { xsqrt { 1 – { x^2 } } dx } } = { intlimits_1^0 { sqrt w left( { – frac { { dw } } { 2 } }right) } } = { – frac { 1 } { 2 } intlimits_1^0 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { sqrt w dw } } = { frac { 1 } { 2 } intlimits_0^1 { { w^ { largefrac { 1 } { 2 } normalsize } } dw } } = { frac { 1 } { 2 } left. { left( { frac { { 2 { w^ { largefrac { 3 } { 2 } normalsize } } } } { 3 } }right) }right|_0^1 = frac { 1 } { 3 } . } $ Наконец, вычислим третий интеграл. $require { cancel } { { I_3 } = intlimits_0^1 { left( { 1 – 2x + { x^2 } }right)dx } } = { left. { left( { x – { x^2 } + frac { { { x^3 } } } { 3 } }right) }right|_0^1 } = { cancel { 1 } – cancel { 1 } + frac { 1 } { 3 } = frac { 1 } { 3 } . } $ Таким образом, объем тела равен $ { V = { I_1 } – { I_2 } – { I_3 } } = { frac { pi } { 4 } – frac { 1 } { 3 } – frac { 1 } { 3 } = frac { pi } { 4 } – frac { 2 } { 3 } approx 0,12. } $
Пример 7
Вычислить объем единичного шара.
Решение:
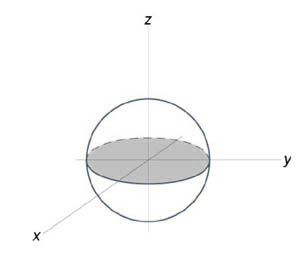
Уравнение сферы радиусом (1) имеет вид ( { x^2 } + { y^2 } + { z^2 } = 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = sqrt { 1 – left( { { x^2 } + { y^2 } }right) } .$ Преобразуя это уравнение в полярные координаты, получаем $zleft( { r,theta }right) = sqrt { 1 – { r^2 } } .$ В полярных координатах область интегрирования (R) описывается множеством (R = left[{ left( { r,theta }right)|;0 le r le 1,0 le theta le 2pi }right].) Следовательно, объем верхнего полушара выражается формулой $ { { V_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 – { r^2 } } rdrdtheta } } = { intlimits_0^ { 2pi } { dtheta } intlimits_0^1 { sqrt { 1 – { r^2 } } rdr } } = { 2pi intlimits_0^1 { sqrt { 1 – { r^2 } } rdr } . } $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 – { r^2 } = t.) Тогда (-2rdr = dt) или (rdr = – largefrac { { dt } } { 2 } normalsize.) Уточним пределы интегрирования: (t = 1) при (r = 0) и, наоборот, (t = 0) при (r = 1.) Получаем $ { { V_ { largefrac { 1 } { 2 } normalsize } } = 2pi intlimits_0^1 { sqrt { 1 – { r^2 } } rdr } } = { 2pi intlimits_1^0 { sqrt t left( { – frac { { dt } } { 2 } }right) } } = { – pi intlimits_1^0 { sqrt t dt } } = { pi intlimits_0^1 { { t^ { largefrac { 1 } { 2 } normalsize } } dt } } = { pi left. { left( { frac { { { t^ { largefrac { 3 } { 2 } normalsize } } } } { { frac { 3 } { 2 } } } }right) }right|_0^1 } = { frac { { 2pi } } { 3 } . } $ Таким образом, объем единичного шара равен $V = 2 { V_ { largefrac { 1 } { 2 } normalsize } } = frac { { 4pi } } { 3 } .$
Пример 8
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).
Решение:
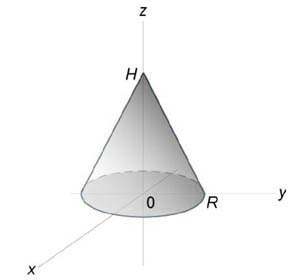
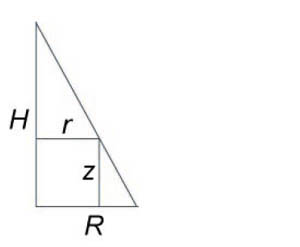
Сначала получим уравнение поверхности конуса. Используя подобные треугольники, можно записать $ { frac { r } { R } = frac { { H – z } } { H } , } ;; { text { где } ;;r = sqrt { { x^2 } + { y^2 } } . } $ Следовательно, $ { H – z = frac { { Hr } } { R } } ;; { text { или } ;;zleft( { x,y }right) } = { H – frac { { Hr } } { R } } = { frac { H } { R } left( { R – r }right) } = { frac { H } { R } left( { R – sqrt { { x^2 } + { y^2 } } }right). } $ Тогда объем конуса равен $ { V = iintlimits_R { zleft( { x,y }right)dxdy } } = { iintlimits_R { frac { H } { R } left( { R – sqrt { { x^2 } + { y^2 } } }right)dxdy } } = { frac { H } { R } iintlimits_R { left( { R – r }right)rdrdtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { left[ { intlimits_0^R { left( { R – r }right)drd } }right]dtheta } } = { frac { H } { R } intlimits_0^ { 2pi } { dtheta } intlimits_0^R { left( { Rr – { r^2 } }right)dr } } = { frac { { 2pi H } } { R } intlimits_0^R { left( { Rr – { r^2 } }right)dr } } = \ = { frac { { 2pi H } } { R } left. { left( { frac { { R { r^2 } } } { 2 } – frac { { { r^3 } } } { 3 } }right) }right|_ { r = 0 } ^R } = { frac { { 2pi H } } { R } left( { frac { { { R^3 } } } { 2 } – frac { { { R^3 } } } { 3 } }right) } = { frac { { 2pi H } } { R } cdot frac { { { R^3 } } } { 6 } = frac { { pi { R^2 } H } } { 3 } . } $
Вычислить объем тела, ограниченного поверхностями.
Пример 1:
Вычислить объем тела, ограниченного поверхностями (по площадям сечений).

Решение от преподавателя:
Строим графики функций:

Тогда объем тела вращения вокруг оси будем находить по формуле:

Ответ: .
.
Пример 2:
Найти объем тела, полученного вращением криволинейной трапеции вокруг оси ОХ.

Решение от преподавателя:

Пример 3:

Решение от преподавателя:

Пример 4:
Вычислить объем тела, ограниченного поверхностями:
![]()
Решение от преподавателя:
Изобразим поверхность:

то есть z меняется от ![]()

Пример 5:
Вычислить объемы тел, ограниченных поверхностями.

Решение от преподавателя:

Пример 6:
Объем тела, ограниченного поверхностью, полученной от вращения дуги кривой ![]() вокруг оси Ох.
вокруг оси Ох.
Решение от преподавателя:
Объем фигуры, образованной в результате вращения вокруг оси Ox криволинейной трапеции, ограниченной непрерывной кривой y = f(x) (a ≤ x ≤ b), Осью Ox и прямыми x= a и x = b, вычисляется по формуле:

Построим график функции:



Пример 7:
Вычислить с помощью двойного интеграла объем тела, ограниченного указанными поверхностями:

Решение от преподавателя:


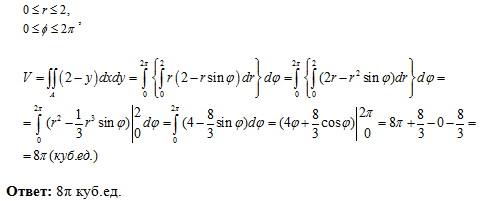
Пример 8:
Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми

Решение от преподавателя:


Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
Примеры решений тройных интегралов
В этом разделе вы найдете подробные решения, связанные и вычислением и применением тройных интегралов: от непосредственного вычисления (в декартовых, цилиндрических, сферических координатах), до применения к нахождению объемов тел, массы, моментов и т.п. Примеры сгруппированы по темам:
Спасибо за ваши закладки и рекомендации
Тройные интегралы: примеры решений
Задача 1. Вычислить тройной интеграл
$$iiint_V x^2yz dx dy dz, quad V: -1 le x le 2, 0le y le 3, 2 le z le 3. $$
Задача 2. Переходя к сферическим координатам, вычислить интеграл
$$iiint_V x^2 dxdydz, quad V: x^2+y^2+z^2=R^2,, zge 0, xgt 0.$$
Задача 3. Переходя к цилиндрическим координатам вычислить интеграл
$$iiint_V x^2 dxdydz, quad V: x^2+y^2=x,, z=x^2+y^2, z=0.$$
Задача 4. Решить тройной интеграл двумя способами (цилидрическая и сферическая замена координат)
$$iiint_G(x^2+y^2+z^2)^2 dxdydz,quad G={(x,y,z):x^2+y^2+z^2le a^2,x+zge0}$$
Трудности с задачами? МатБюро поможет с интегралами.
Объемы тел: примеры решений
Задача 5. Найти объем тела, заданного ограничивающими его поверхностями (внутри цилиндра).
$$z=sqrt{100-x^2-y^2},, z=6,, x^2+y^2=51$$
Задача 6. Найти объем тела, ограниченного поверхностями
$$x^2+y^2=9x, x^2+y^2=12x, z=sqrt{x^2+y^2}, z=0, y ge 0.$$
Задача 7. Вычислить тройным интегрированием объем тела, ограниченного данными поверхностями:
$$z=2-x, z=0, y=sqrt{x}, y=frac{1}{4}x^2.$$
Задача 8. Найти объем тела, ограниченного координатными плоскостями и поверхностью
$$
left(frac{x}{a}+ frac{y}{b} + frac{z}{c} right)^3 = sin left(pi frac{frac{x}{a}+ frac{y}{b}}{frac{x}{a}+ frac{y}{b} + frac{z}{c} } right)
$$
Задача 9. Найти объем тела, ограниченного поверхностью $x^2+y^2+z^2=2x+3y$.
Моменты, масса тела: примеры решений
Задача 10. Найти статический момент относительно $xOy$ однородного тела, ограниченного поверхностью
$$(x^2+y^2+z^2 )^3=frac{x^2+y^2}{z^2} $$
с плотностью $z=0$ $(z ge 0)$.
Задача 11. Используя тройной интеграл в цилиндрической системе координат, вычислить массу кругового цилиндра, нижнее основание которого лежит в плоскости $xOy$, а ось симметрии совпадает с осью $Oz$, если заданы радиус основания $R$, высота цилиндра $H$ и функция плотности $gamma(rho)$, где $rho$ – полярный радиус точки.
$$ R=2, H=0,5, gamma=2+rho^2+rho^3.$$
Задача 12. Найти массу тела, заданного системой неравенств, если плотность тела в каждой точке задана функцией $mu$.
$$ frac{1}{2}sqrt{x^2+y^2} le z le sqrt{4-x^2-y^2}, quad mu =frac{5}{8}z. $$
Задача 13. Найти момент инерции относительно оси Oz тела, ограниченного заданными поверхностями.
$$z=-x^2-y^2, z=x^2+y^2-8$$
Не берется интеграл? Вычислим быстро и подробно поясним!
Полезные ссылки
- Интегралы – примеры решений
- Применение интегралов – примеры решений
- Двойные интегралы – примеры решений
- Криволинейные интегралы – примеры решений
- Поверхностные интегралы – примеры решений
- Учебник с примерами онлайн по тройным интегралам
Тройные интегралы в прямоугольных координатах
Краткая теория
Тройным
интегралом от функции
, распространенным на
область
, называется предел
соответствующей трехкратной суммы:
Вычисление
тройного интеграла сводится к последовательному вычислению трех обыкновенных
(однократных) интегралов или к вычислению одного двойного и одного
однократного.
Основные
свойства тройных интегралов аналогичны свойствам двойных интегралов.
Объем
тела
в декартовых координатах
выражается формулой:
Примеры решения задач
Задача 1
Вычислить
тройной интеграл:
Решение
Ответ:
Задача 2
Вычислить
объем тела, ограниченного данными поверхностями. Сделать чертежи данного тела и
его проекции на плоскость
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Сделаем
чертеж тела:
Проекция
тела на
:
Искомый объем тела будет выражаться
интегралом:
Ответ:
Задача 3
Вычислить объем тела,
ограниченного заданными поверхностями:
Решение
Сделаем чертеж тела:
Проекция тела на
:
Искомый объем тела
будет выражаться интегралом:
Ответ:
