Как найти объем тела онлайн калькулятор

Как найти объем тела онлайн калькулятор

Объем геометрических фигур

Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).

Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.

Объем куба

Размеры куба

Размеры куба

Формула: V=H^3

PLANETCALC, Объем куба

Объем куба

Точность вычисления

Знаков после запятой: 5

Объем прямоугольной призмы

Размеры прямоугольной призмы

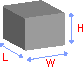
Размеры прямоугольной призмы

Формула: V=HWL

PLANETCALC, Объем прямоугольной призмы

Объем прямоугольной призмы

Точность вычисления

Знаков после запятой: 5

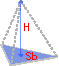
Объем пирамиды

Размеры пирамиды

Размеры пирамиды

Формула: V={1 over 3} Sb H

PLANETCALC, Объем пирамиды

Объем пирамиды

Точность вычисления

Знаков после запятой: 5

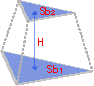
Объем усеченной пирамиды

Размеры усеченной пирамиды

Размеры усеченной пирамиды

Формула: V={Hover3}(S_{b1}+S_{b2}+sqrt{S_{b1} S_{b2}})

PLANETCALC, Объем усеченной пирамиды

Объем усеченной пирамиды

Площадь первого основания (Sb1)

Площадь второго основания (Sb2)

Точность вычисления

Знаков после запятой: 5

Объем конуса

Размеры конуса

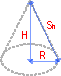
Размеры конуса

Формула: V={1 over 3}pi{R}^2 H

PLANETCALC, Объем конуса

Объем конуса

Точность вычисления

Знаков после запятой: 5

Объем цилиндра

Размеры цилиндра

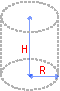
Размеры цилиндра

Formula: V=pi R^2 H

PLANETCALC, Объем цилиндра

Объем цилиндра

Точность вычисления

Знаков после запятой: 5

Объем сферы

Размеры сферы

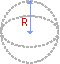
Размеры сферы

Формула: V={4 over 3} pi R^3

PLANETCALC, Объем сферы

Объем сферы

Точность вычисления

Знаков после запятой: 5

Объем эллипсоида

Размеры эллипсоида

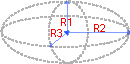
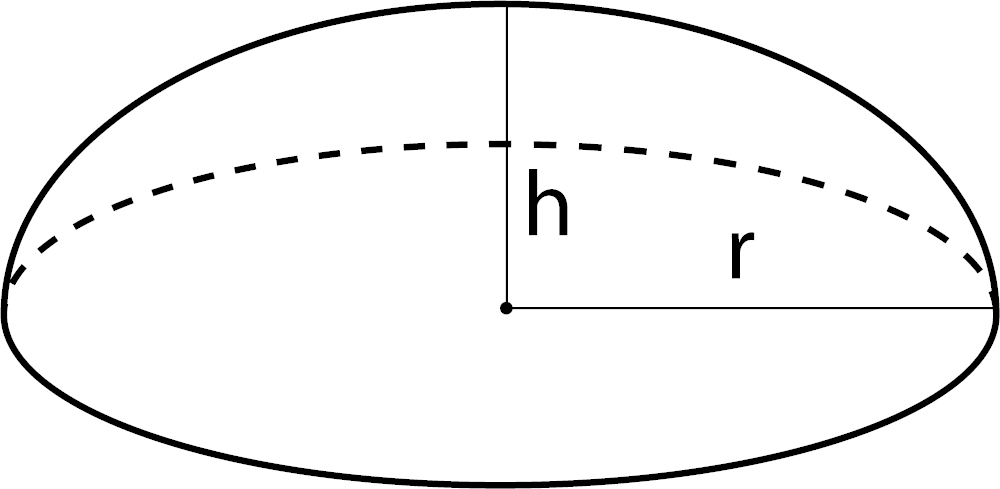
Размеры эллипсоида

Формула: V={4 over 3} pi R_1 R_2 R_3

PLANETCALC, Объем эллипсоида

Объем эллипсоида

Точность вычисления

Знаков после запятой: 5

Объем тороида

Размеры тороида

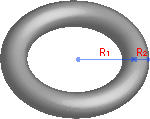
Размеры тороида

Формула: V=2 pi^2 R_1 R_2^2

PLANETCALC, Объем тора

Объем тора

Точность вычисления

Знаков после запятой: 5

Ссылка скопирована в буфер обмена

PLANETCALC, Объем геометрических фигур

Источник

Калькуляторы объема от КАЛК.ПРО предоставляют возможность выполнить точный расчет кубатуры геометрических фигур и реальных предметов по базовым формулам тригонометрии, стереометрии, начертательной и Евклидовой геометрии. Инструменты будут полезны как в научной деятельности при определении объема цилиндра, пирамиды, конуса… так и в практической деятельности при необходимости рассчитать грузы, емкости, сооружения. Все расчеты сопровождаются подробным описанием алгоритма, формулами и примерами. Результаты предоставляются в условных единицах или в единицах СИ.

Единицы измерения объема (СИ)

  • 1 мм3 (куб. миллиметр) = 0.000000001 м3;
  • 1 см3 (куб. сантиметр) = 0.000001 м3;
  • 1 дм3 (куб. дециметр / литр) = 0.001 м3;
  • 1 км3 (куб. километр) = 1.000.000.000 м3.

Единицы измерения объема (внесистемные и имперские)

  • 1 мл (миллилитр) = 0.001 л = 0.000001 м3;
  • 1 л (литр) = 0.001 м3;
  • 1 унция (англ.) = 28.413 мл = 0.028413 л = 0.000028413 м3;

  • 1 унция (амер.) = 29.573 мл = 0.029573 л = 0.000029573 м3;

  • 1 галлон (англ.) = 4.55 литра = 0.00455 м3;

  • 1 галлон (амер.) = 3.785 литра = 0.00378541 м3;

  • 1 дюйм3 = 0,0000163871 м3;

  • 1 фут3 = 0.0283168 м3;
  • 1 ярд3 = 0,76455 м3.

Для того чтобы начать расчет объема, выберите необходимый калькулятор:

Источник

Многие сложные детали (конструкции) можно представить совокупностью различных элементов, объем которых можно вычислить, воспользовавшись набором online-калькуляторов с данной страницы.

Представлены программы для расчета объемов фигур, базисом которых является квадрат или прямоугольник, а также имеющих в основании окружность: цилиндра, конуса и шаровых элементов.

В конструкторской работе при различных расчетах возникает потребность использования значений объема элементарных фигур: параллелепипеда, куба, призмы и пр. В частности это может иметь место при расчете заполнения вагонов и платформ упакованной в транспортную тару готовой продукцией. Такой расчет требует учета многих факторов, в том числе боковой ветровой нагрузки, смещения центра тяжести и пр.

Если неправильно рассчитать объем тары подлежащего отгрузке упакованного товара, можно не вместить в вагон заявленное количество изделий. В результате предприятие потерпит убытки. Онлайн калькуляторы нашего сайта позволят избежать проблемных ситуаций. Расчеты объемов различных фигур выполняются с большой точностью.

Источник

Калькулятор для расчета объема параллелепипеда

C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер “a”, “b”, “c” и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.

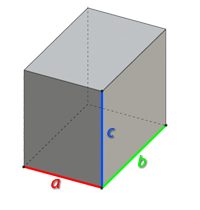
Расчет объема параллелепипеда

Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку “Рассчитать”

Округлить результат до

знаков после запятой

Рассчитать

Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.

Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
где a, b, c – ребра параллелепипеда.

Источник

Calculate volume by selecting one of the shapes below and entering your measurements in any unit.

How to Find Volume

Volume is the measure of 3-dimensional space that a geometric shape or object occupies. It’s measured in cubic units, such as cubic yards or cubic feet.

Of course, you can find volume easily using a calculator like the one above, but you can also find it by using a formula. Read on to learn more about how to calculate volume yourself.

Volume Formulas

The volume of every shape is calculated differently using a different formula. Below you will find the formulas to find the volume of several three-dimensional shapes.

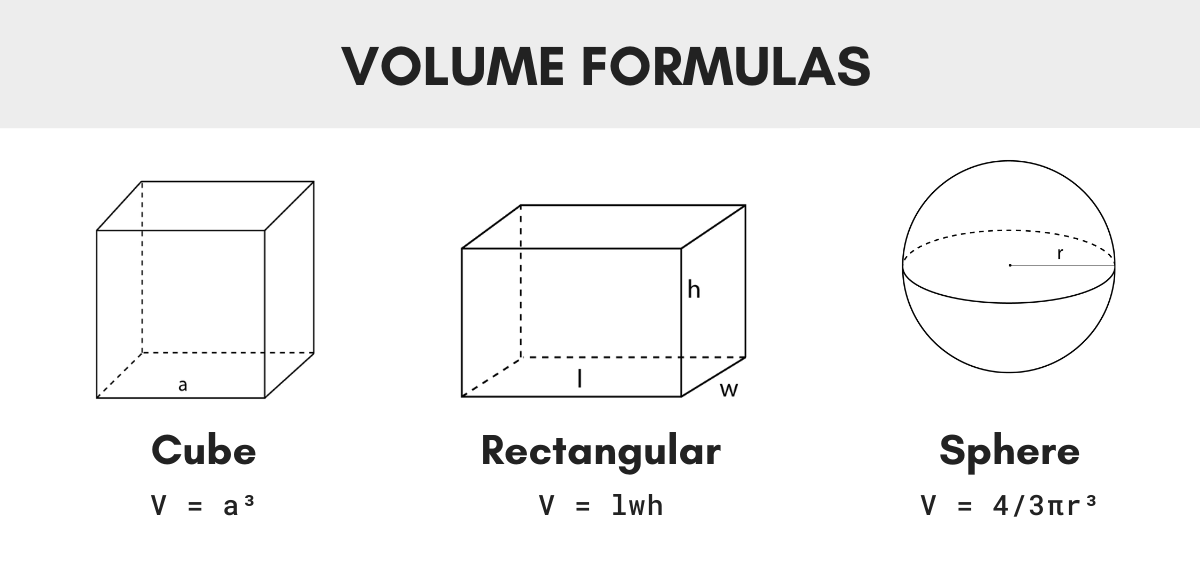
Formulas to find the volume for several shapes

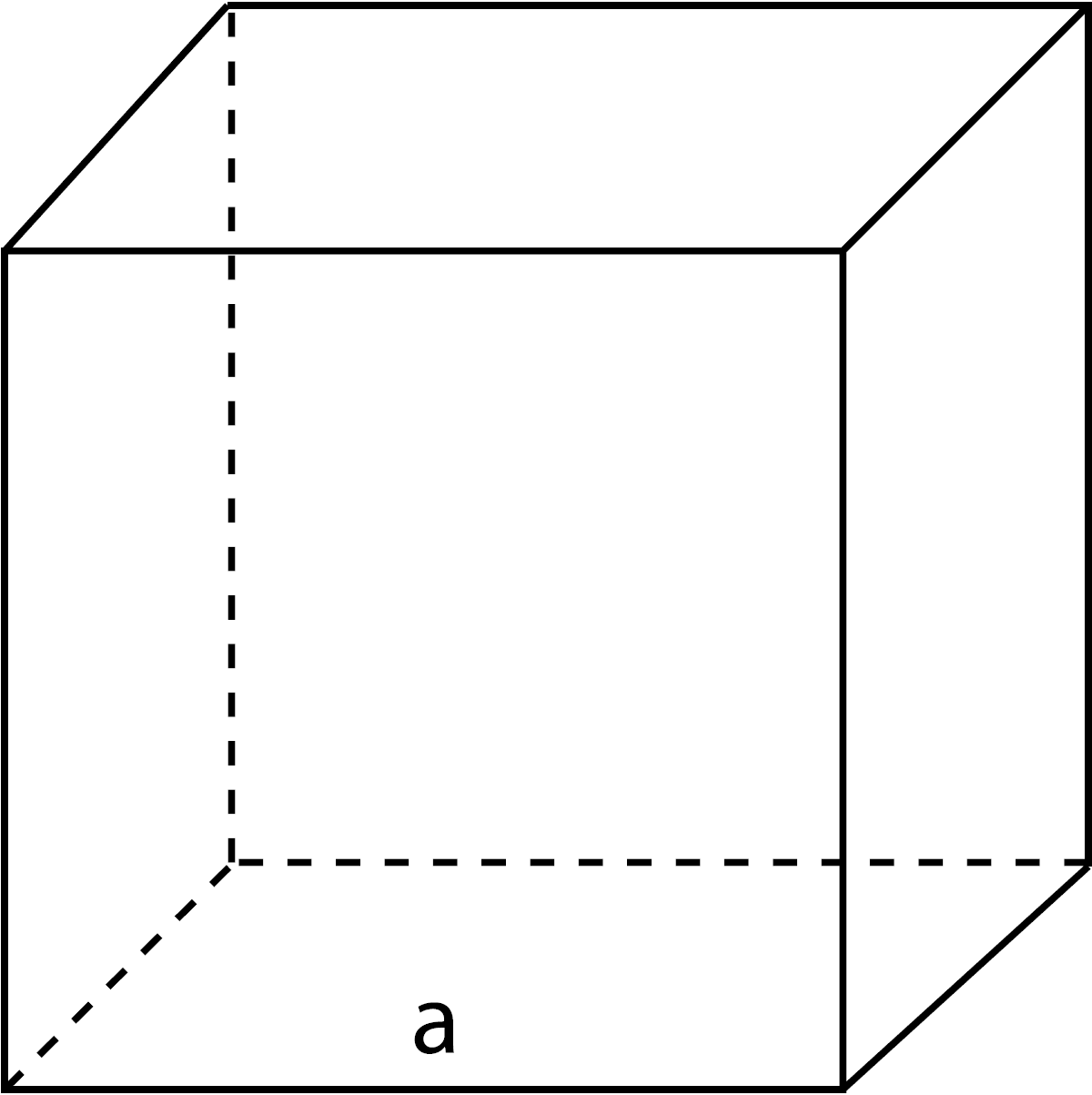
Volume of a Cube

V = a3

a = edge a length

Diagram of a cube showing a = edge length

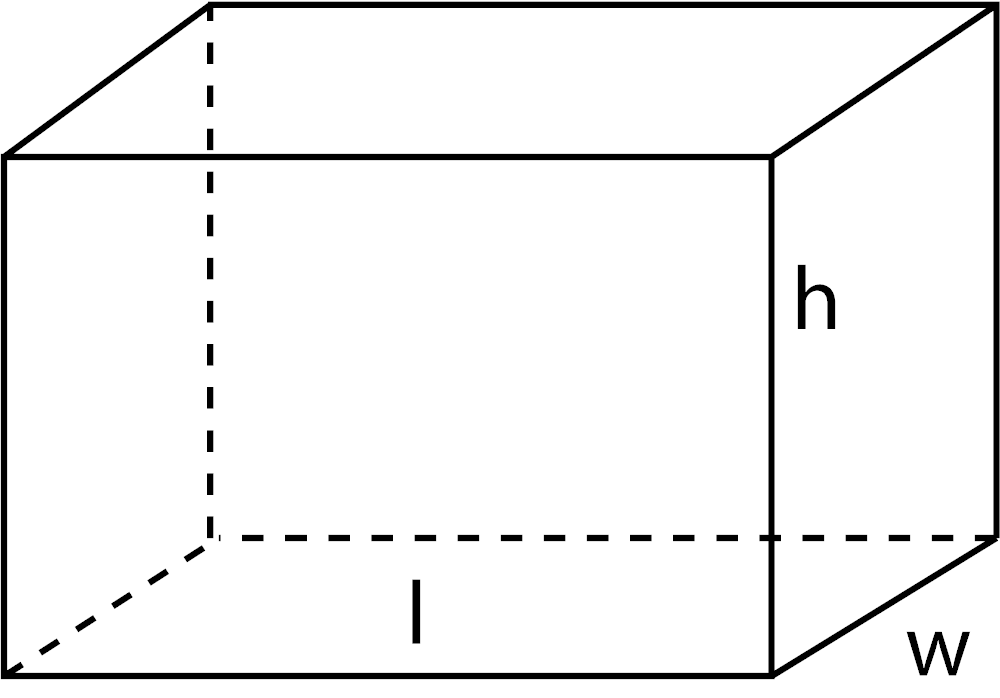
Volume of a Rectangular Prism

V = l × w × h

l = length
w = width
h = height

Diagram of a rectangular prism showing l = length, w = width, and h = height

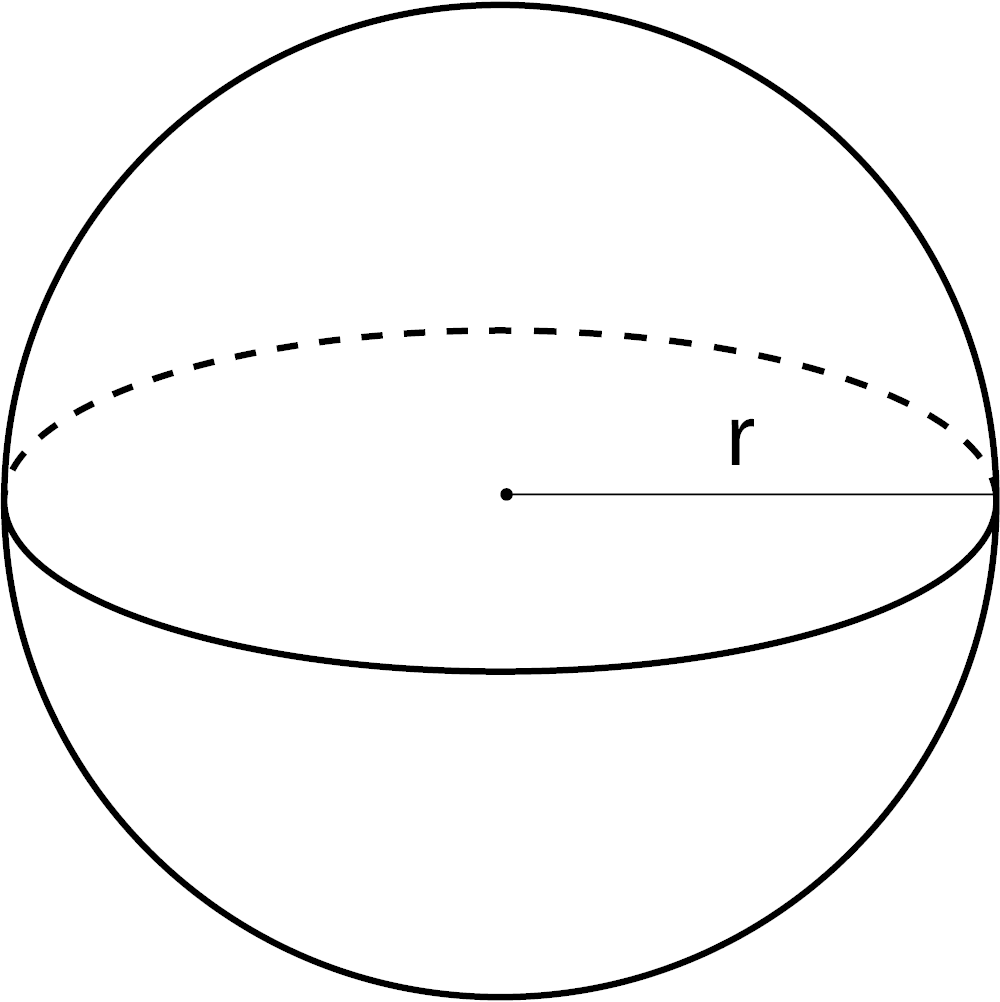
Volume of a Sphere

V = 4 / 3πr3

r = radius

Diagram of a sphere showing r = radius

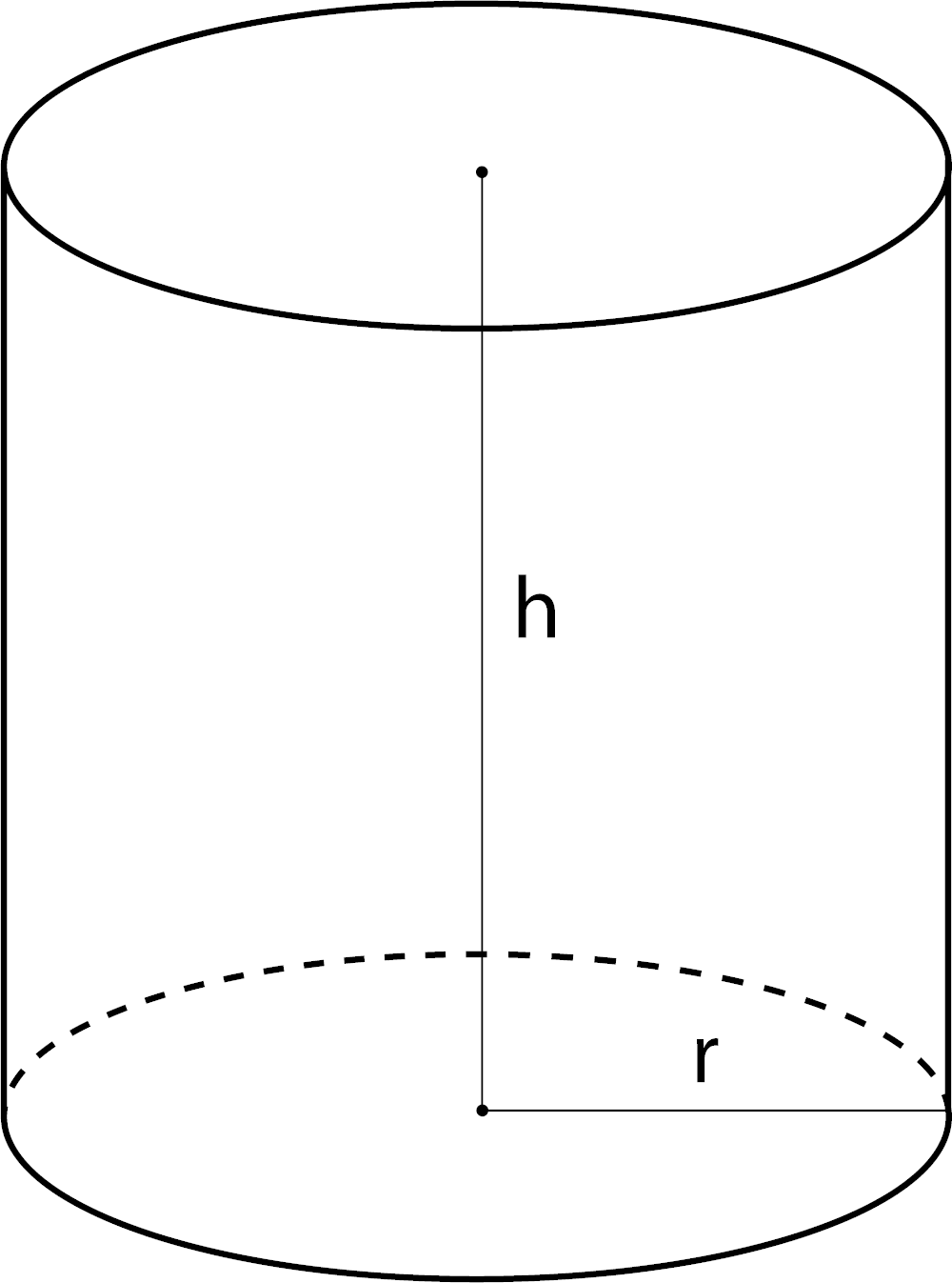
Volume of a Cylinder

V = πr2h

r = radius
h = height

Diagram of a cylinder showing r = radius and h = height

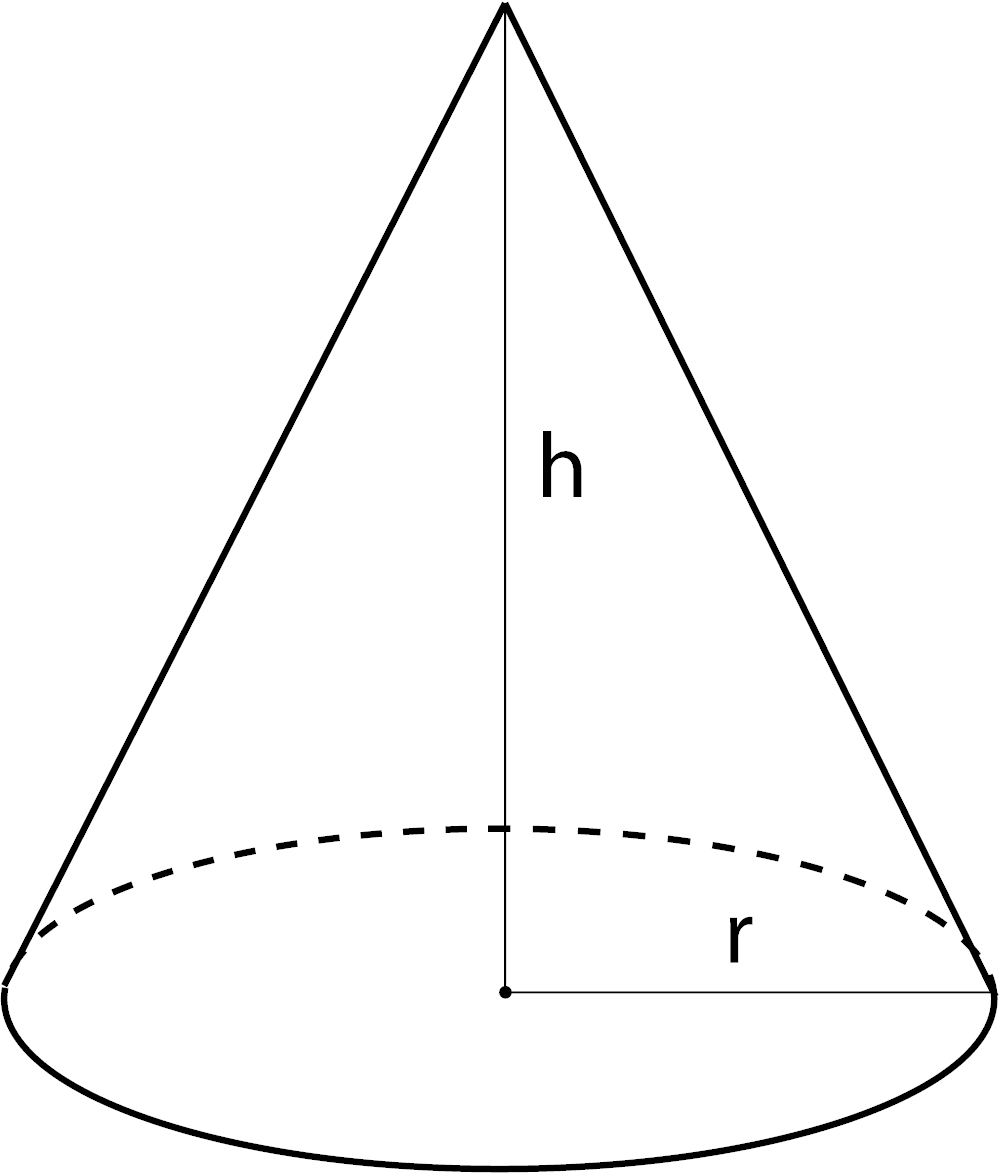
Volume of a Cone

V = 1 / 3πr2h

r = radius
h = height

Diagram of a cone showing r = radius and h = height

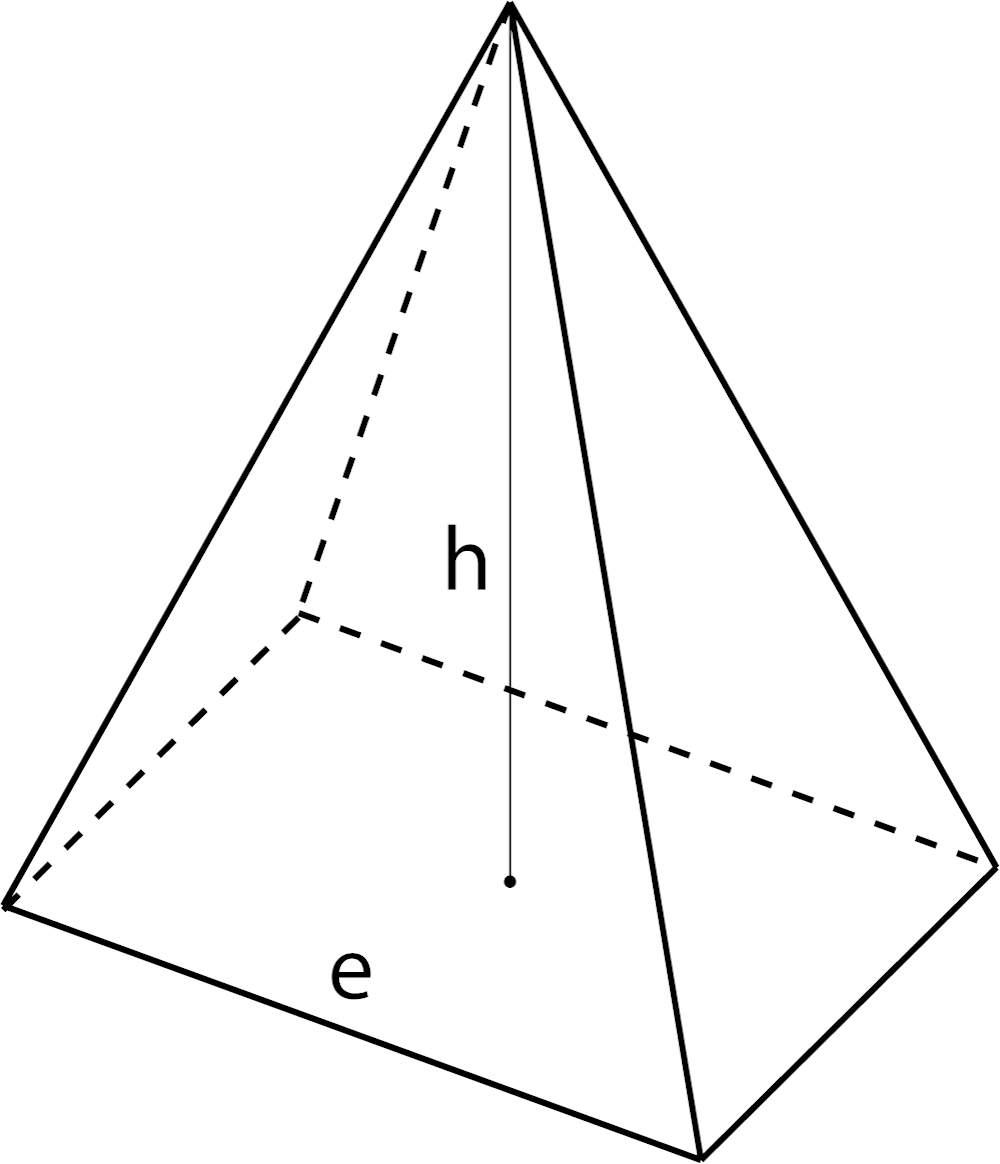
Volume of a Pyramid

V = 1 / 3e2h

e = edge length
h = height

Diagram of a pyramid showing e = edge length and h = height

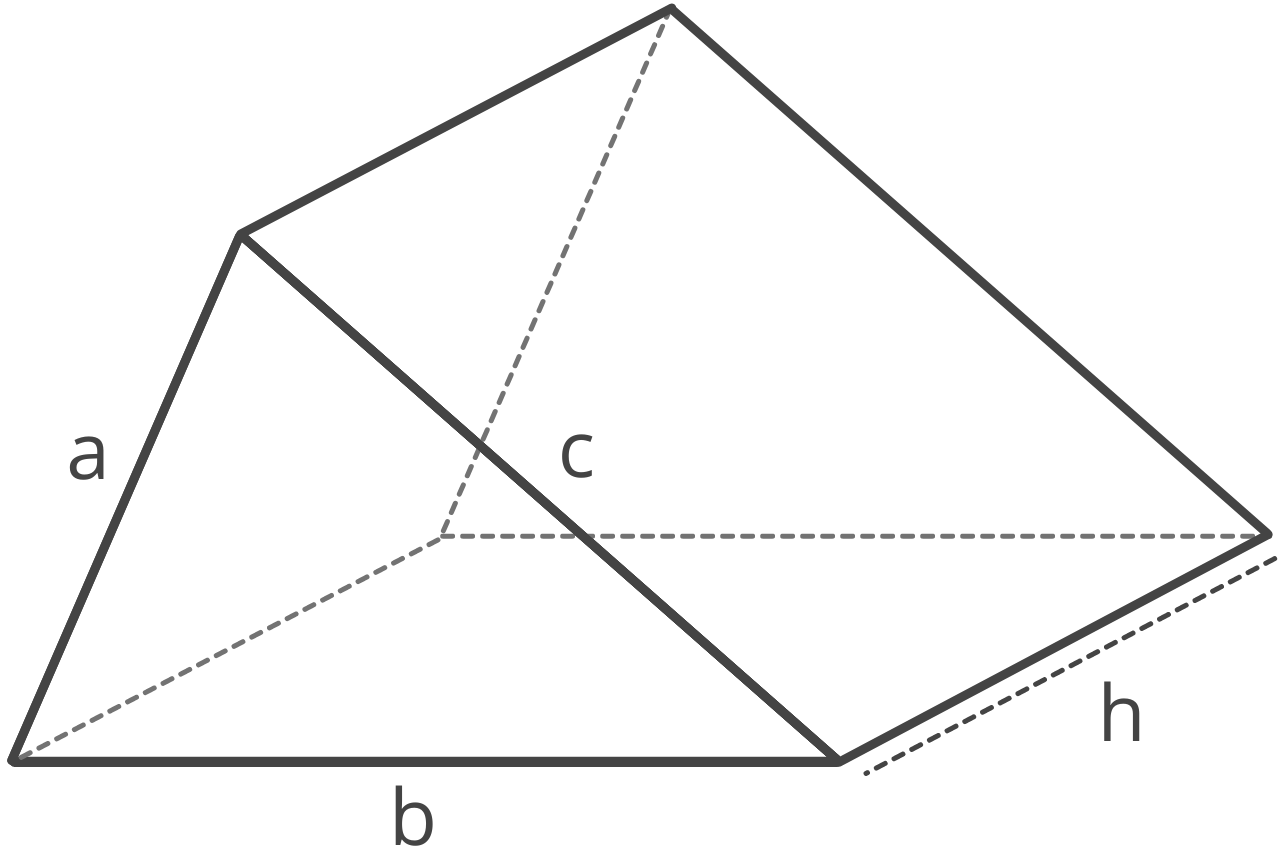
Volume of a Triangular Prism

s = 1/2(a + b + c)
V = h × s(s – a)(s – b)(s – c))

a, b & c = triangle sides

h = height

Diagram of a triangular prism showing sides a, b, & c, and h = height

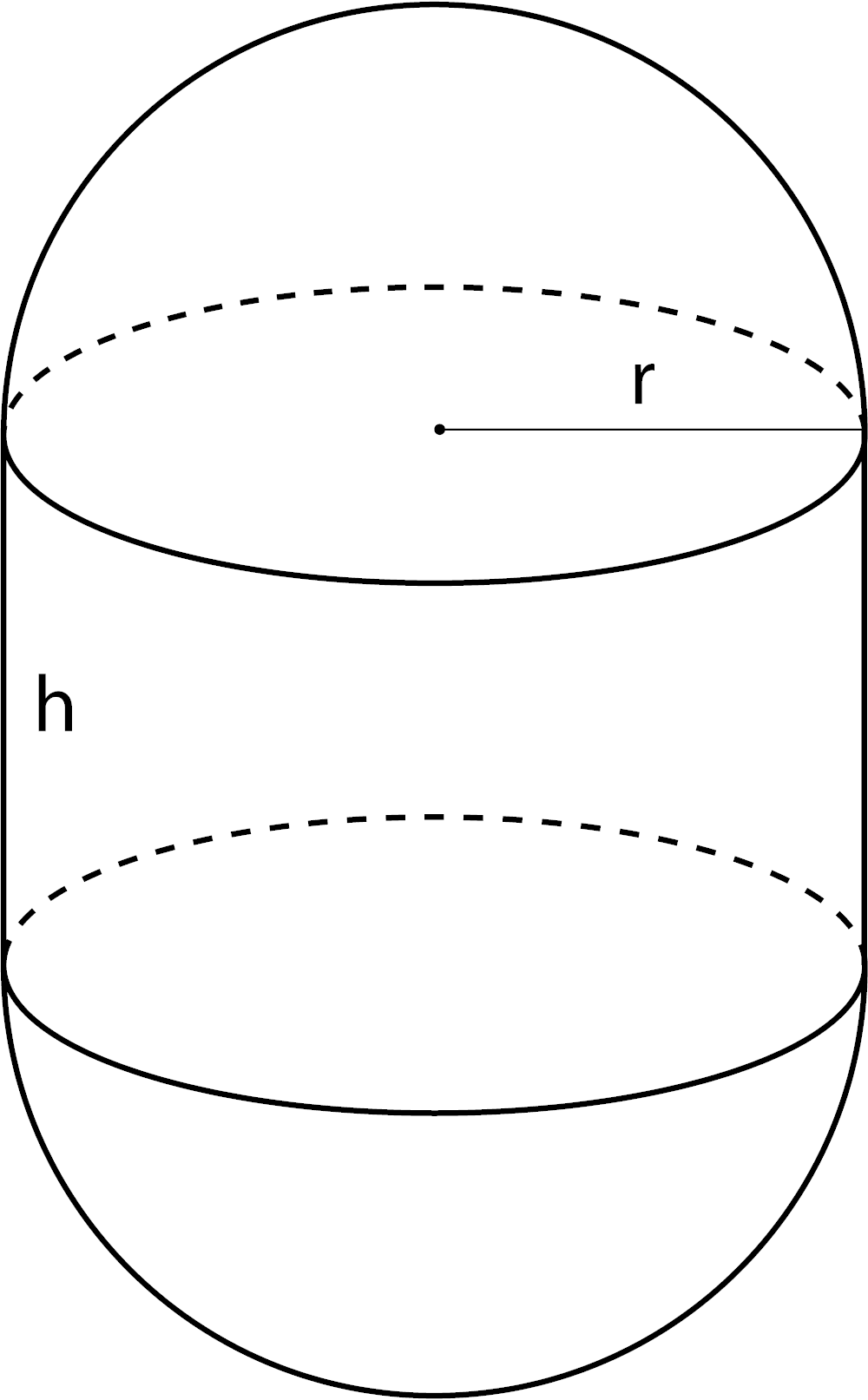
Volume of a Capsule

V = πr2h + 4 / 3πr3

r = radius
h = height

Diagram of a capsule showing r = radius and h = height

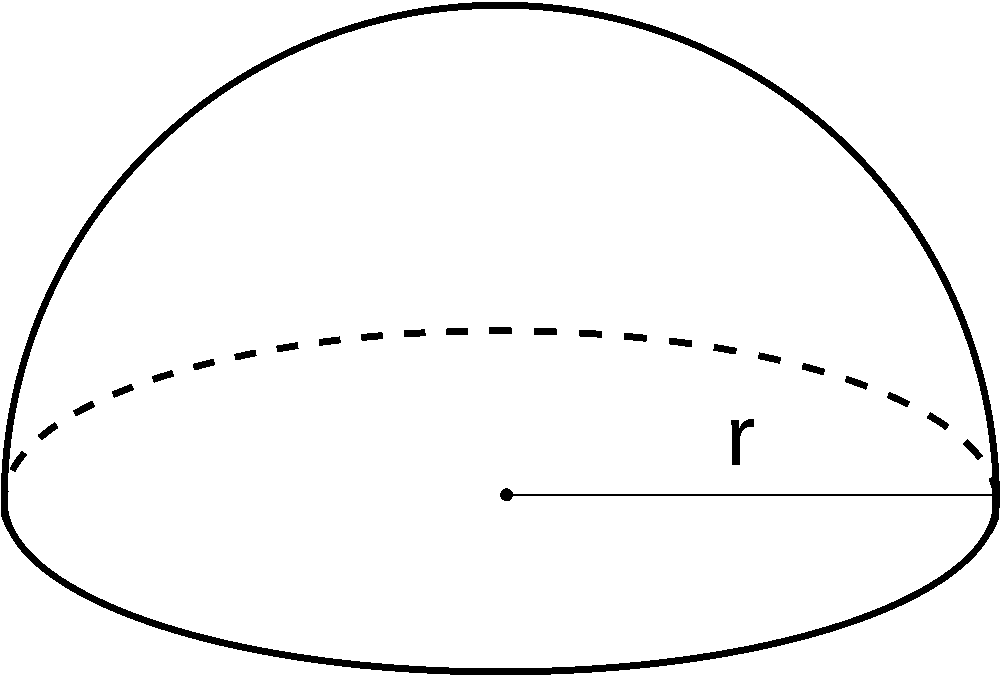
Volume of a Hemisphere

V = 2 / 3πr3

r = radius

Diagram of a hemisphere showing r = radius

Volume of a Spherical Cap

V = π / 6h(3r2 + h2)

r = radius
h = height

Diagram of a cap showing r = radius and h = height

How to Find the Volume of an Irregular Object

The formulas above can be used to calculate regular objects with a defined formula, but many objects are irregular or have no obvious formula. Water displacement is a technique used to find the amount of space an irregular object occupies.

The water displacement technique involves filling a container, that you know the volume of, with water and measuring the amount of water displaced by submerging the irregular object in the water in the container.

For example, fill a container with water and calculate the volume of the water using the formulas above.

Submerge the irregular object in the water and observe that the water level in the container has risen.

Measure the amount of water as before and calculate the volume of the water with the object submerged.

Subtract the initial result by the result after the irregular object was placed in the water to find the volume of the object.

A graduated cylinder is often used for finding the volume of small irregular shaped solids.

Measuring Volume Using Weight

In some cases, you can measure the volume of a fluid or irregular solid material by measuring its mass. If you know the density of the material, you can calculate the volume using its mass with the following formula:

V = m / ρ

where:
V = volume
m = mass
ρ = density

The volume of a material is equal to the mass m divided by its density ρ.

This technique is commonly used to estimate the volume of materials like gravel or water.

Volume Measurement Tips

One important consideration when measuring volume is to take all measurements using the same unit of measure. If your measurements are in different units, convert each measurement to the unit you want the results in.

Use our length converter to convert your measurements to a consistent unit. You can also use our volume converter to convert your result to another unit of measure.

Common Volume Measurements

You might also be interested in our surface area calculator to find the surface area of a shape.

Frequently Asked Questions

What does volume tell us about an object?

Volume tells us the amount of space an object takes up.

Why is volume cubed?

Volume is measured in cubic units because it is measured using three dimensions. All three dimensions must be multiplied to get the volume.

Why is the volume of sphere 4/3πr³?

Since a sphere is three-dimensional the formula has to be cubed.

How is volume used in real life?

Is volume the same as weight?

No, volume is not the same as weight. Volume is the amount of space an object takes up, while weight is the heaviness of the object.

Источник

Добавить комментарий