Объём тела вращения
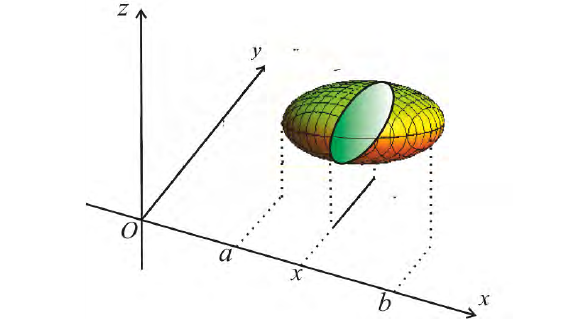
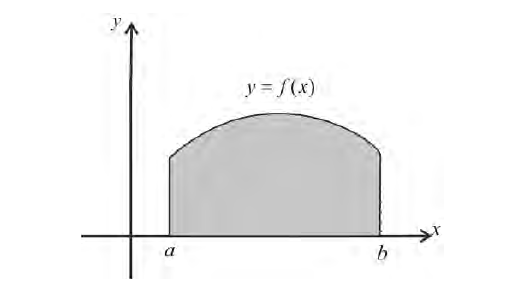
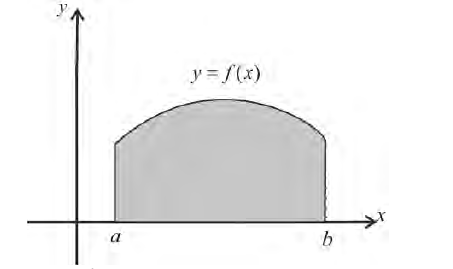
Пусть — тело вращения, образованное вращением вокруг оси абсцисс криволинейной трапеции, расположенной в верхней полуплоскости и ограниченной осью абсцисс, прямыми
и
и графиком непрерывной функции
.
Докажем, что это тело вращения кубируемо и его объем выражается формулой
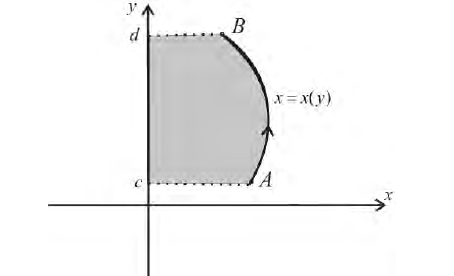
Сначала докажем, что это тело вращения регулярно, если в качестве выберем плоскость
, перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстоянии
от плоскости
, является кругом радиуса
и его площадь
равна
(рис. 46). Поэтому функция
непрерывна в силу непрерывности
. Далее, если
, то это значит, что
. Но проекциями сечений на плоскость
являются круги радиусов
и
с центром
, и из
вытекает, что круг радиуса
содержится в круге радиуса
.
Итак, тело вращения регулярно. Следовательно, оно кубируемо и его объем вычисляется по формуле
Если бы криволинейная трапеция была ограничена и снизу и сверху кривыми
, то
Формулой (3) можно воспользоваться и для вычисления объема тела вращения в случае, когда граница вращающейся фигуры задана параметрическими уравнениями. В этом случае приходится пользоваться заменой переменной под знаком определенного интеграла.
В некоторых случаях оказывается удобным разлагать тела вращения не на прямые круговые цилиндры, а на фигуры иного вида.
Например, найдем объем тела, получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдем объем, получаемый при вращении прямоугольника с высотой y#, в основании которого лежит отрезок . Этот объем равен разности объемов двух прямых круговых цилиндров
Но теперь ясно, что искомый объем оценивается сверху и снизу следующим образом:
Отсюда легко следует формула объёма тела вращения вокруг оси ординат:
(4)
Пример 4. Найдем объем шара радиуса .
Решение. Не теряя общности, будем рассматривать круг радиуса с центром в начале координат. Этот круг, вращаясь вокруг оси
, образует шар. Уравнение окружности имеет вид
, поэтому
. Учитывая симметрию круга относительно оси ординат, найдем сначала половину искомого объема
Следовательно, объем всего шара равен .
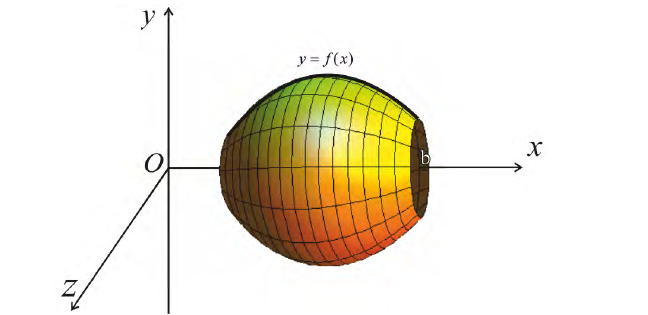
Пример 5. Вычислить объем конуса, высота которого и радиус основания
.
Решение. Выберем систему координат так, чтобы ось совпала с высотой h (рис. 47), а вершину конуса примем за начало координат. Тогда уравнение прямой
запишется в виде
.
Пользуясь формулой (3), получим:
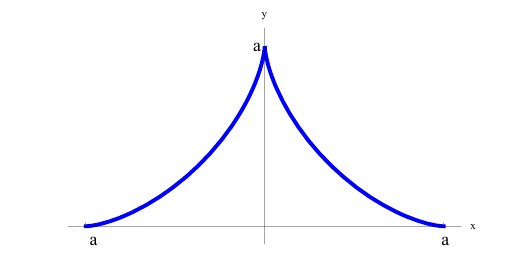
Пример 6. Найдем объем тела, полученного при вращении вокруг оси абсцисс астроиды (рис. 48).
Решение. Построим астроиду. Рассмотрим половину верхней части астроиды, расположенной симметрично относительно оси ординат. Используя формулу (3) и меняя переменную под знаком определенного интеграла, найдем для новой переменной пределы интегрирования.
Если , то
, а если
, то
. Учитывая, что
и
, получаем:
Объем всего тела, образованного вращением астроиды, будет .
Пример 7. Найдем объем тела, получаемого при вращении вокруг оси ординат криволинейной трапеции, ограниченной осью абсцисс и первой аркой циклоиды .
Решение. Воспользуемся формулой (4): , и заменим переменную под знаком интеграла, учитывая, что первая арка циклоиды образуется при изменении переменной
от
до
. Таким образом,
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Пусть Т — тело вращения, образованное вращением вокруг оси абсцисс криволинейной трапеции, расположенной в верхней полуплоскости и ограниченной осью абсцисс, прямыми  графиком непрерывной функции
графиком непрерывной функции 
Докажем, что это тело вращения кубируемо и его объем выражается формулой


Рис. 46
Сначала докажем, что это тело вращения регулярно, если в качестве П выберем плоскость  перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстоянии
перпендикулярную оси вращения. Отметим, что сечение, находящееся на расстоянии  от плоскости
от плоскости  является кругом радиуса
является кругом радиуса  и его площадь
и его площадь  равна
равна  (рис. 46). Поэтому функция
(рис. 46). Поэтому функция  непрерывна в силу непрерывности
непрерывна в силу непрерывности  Далее, если
Далее, если  то это значит, что
то это значит, что  Но проекциями сечений на плоскость
Но проекциями сечений на плоскость  являются круги радиусов
являются круги радиусов  с центром О, и из
с центром О, и из  вытекает, что круг радиуса
вытекает, что круг радиуса  содержится в круге радиуса
содержится в круге радиуса 
Итак, тело вращения регулярно. Следовательно, оно кубируемо и его объем вычисляется по формуле

Если бы криволинейная трапеция была ограничена и снизу и сверху кривыми  то
то

Формулой (3) можно воспользоваться и для вычисления объема тела вращения в случае, когда граница вращающейся фигуры задана параметрическими уравнениями. В этом случае приходится пользоваться заменой переменной под знаком определенного интеграла.
В некоторых случаях оказывается удобным разлагать тела вращения не на прямые круговые цилиндры, а на фигуры иного вида.
Например, найдем объем  получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдем объем, получаемый при вращении прямоугольника с высотой
получаемого при вращении криволинейной трапеции вокруг оси ординат. Сначала найдем объем, получаемый при вращении прямоугольника с высотой  в основании которого лежит отрезок
в основании которого лежит отрезок  Этот объем равен разности объемов двух прямых круговых цилиндров
Этот объем равен разности объемов двух прямых круговых цилиндров

Но теперь ясно, что искомый объем оценивается сверху и снизу следующим образом:

Отсюда легко следует, что

Пример 4. Найдем объем шара радиуса 
Решение. Не теряя общности, будем рассматривать круг радиуса  с центром в начале координат. Этот круг, вращаясь
с центром в начале координат. Этот круг, вращаясь

Рис. 47
вокруг оси  образует шар. Уравнение окружности имеет вид
образует шар. Уравнение окружности имеет вид  поэтому
поэтому  Учитывая симметрию круга относительно оси ординат, найдем сначала половину искомого объема
Учитывая симметрию круга относительно оси ординат, найдем сначала половину искомого объема

Следовательно, объем всего шара равен 
Пример 5. Вычислим объем конуса, высота которого  и радиус основания
и радиус основания 
Решение. Выберем систему координат так, чтобы ось  совпала с высотой
совпала с высотой  (рис. 47), а вершину конуса примем за начало координат. Тогда уравнение прямой О А запишется в виде
(рис. 47), а вершину конуса примем за начало координат. Тогда уравнение прямой О А запишется в виде  Пользуясь формулой (3), получим:
Пользуясь формулой (3), получим:

Пример 6. Найдем объем тела, полученного при вращении вокруг оси абсцисс астроиды  (рис. 48).
(рис. 48).
Решение. Построим астроиду. Рассмотрим половину верхней части астроиды, расположенной симметрично относительно оси ординат. Используя формулу (3) и меняя переменную под знаком определенного интеграла, найдем для новой переменной  пределы интегрирования.
пределы интегрирования.
Если 
Учитывая, что  получаем:
получаем:


Рис. 48

Применяя рекуррентную формулу (см. с. 22), получаем, что

Объем всего тела вращения будет — 
Пример 7. Найдем объем тела, получаемого при вращении вокруг оси ординат криволинейной трапеции, ограниченной осью абсцисс и первой аркой циклоиды 
Решение. Воспользуемся формулой (4):

и заменим переменную под знаком интеграла, учитывая, что первая арка циклоиды образуется при изменении переменной  от 0 до
от 0 до  Таким образом,
Таким образом,

Вопросы для самопроверки
1. Какое тело называется ступенчатым?
2. Какое тело называется кубируемым?
3. Что называется объемом тела?
4. Сформулируйте необходимое и достаточное условие кубируемости тела.
5. Какими свойствами обладает объем тела?
6. Как определяется прямое цилиндрическое тело?
7. Как вычисляется объем прямого цилиндрического тела?
8. Какое тело называется регулярным?
9. Чему равен объем регулярного тела?
10. В чем состоит принцип Кавальери?
И. Какое тело называется телом вращения?
12. Как находится объем тела, полученного от вращения фигуры вокруг одной из координатных осей? Рассмотрите различные случаи задания границы данной фигуры.
Упражнения
(см. скан)
(см. скан)
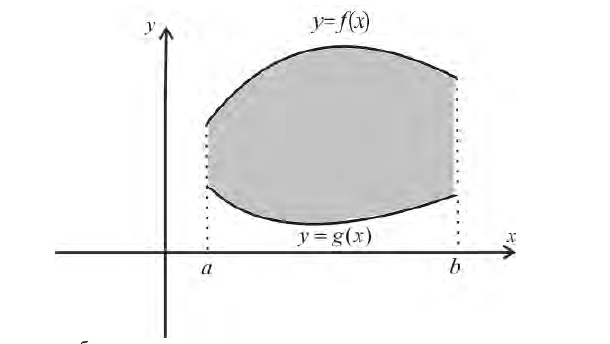
Пусть
– стандартная относительно оси
область. Если ось
не пересекает область
,
то объем тела, образованное вращением
области
вокруг оси
равна

,
если ось
не пересекает область
,
то объем тела, образованное вращением
области
вокруг оси
равна
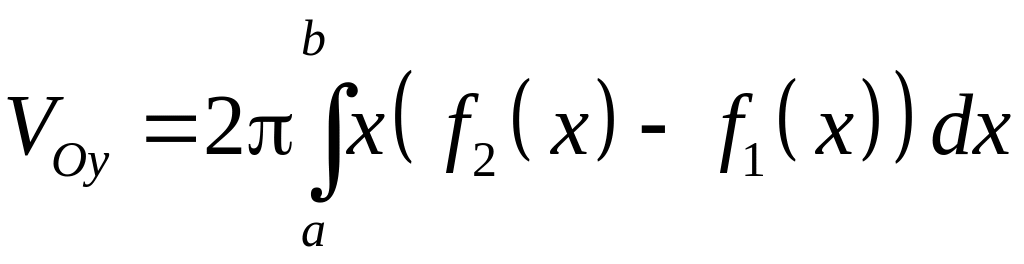
.
Если область
ограничена непрерывной замкнутой
кривой, заданной параметрически
,
причем при изменении
от
![]()
до
![]()
кривая
![]()
проходится так, что область
остается слева. Если область
не пересекается с соответствующей осью
координат и функции
и
непрерывно дифференцируемы на
![]()
,
то
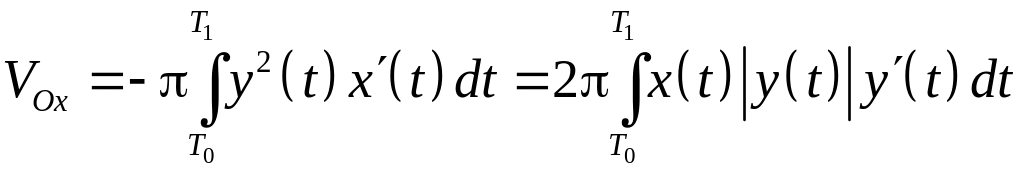
,
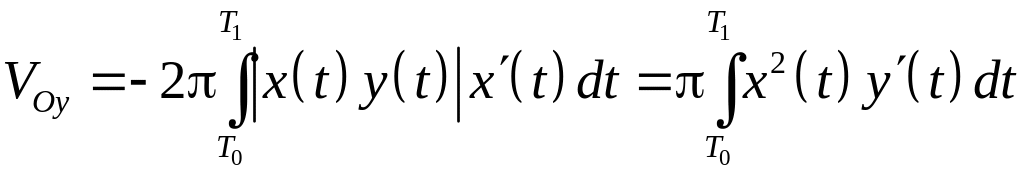
.
Примеры:
6.2.1. Вычислить
объём тела, полученного вращением
параболы
![]()
вокруг осей
и
,
ограниченного прямыми
и
![]()
.
n
Так как
,
![]()
,
![]()
,
то объем тела, полученного вращением
параболы вокруг
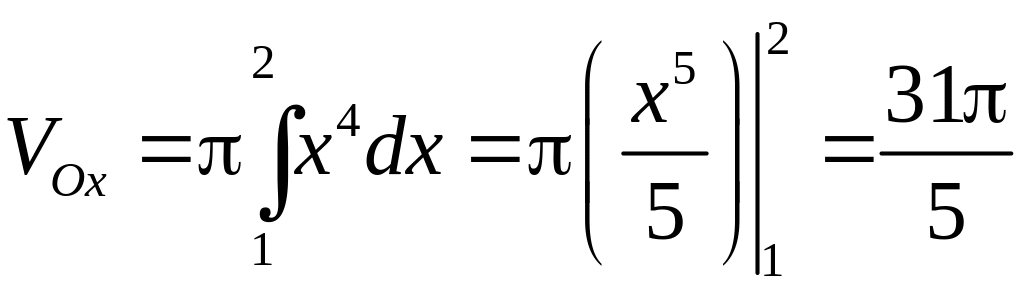
,
вокруг
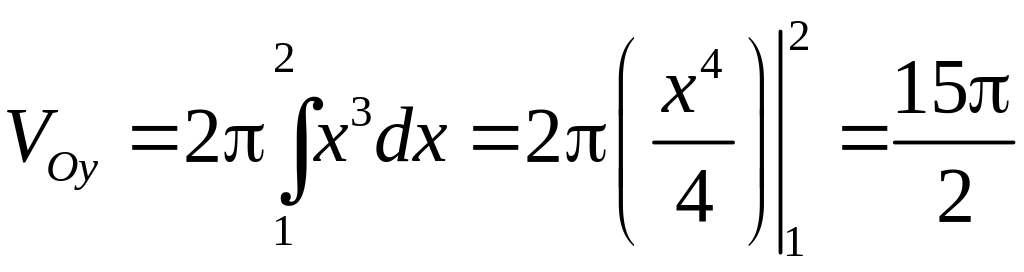
.
6.2.2. Вычислить
объем удлиненного и укороченного
эллипсоида, образованного вращением
эллипса

вокруг осей абсцисс (удлиненный эллипсоид)
и ординат (укороченный эллипсоид).
n
Используем параметрическое параметрическое
представление эллипса
,
.
Вычисляя производные
![]()
,
![]()
.
Тогда, при изменении
от
до
,
получаем для удлиненного эллипса


,
а для укороченного
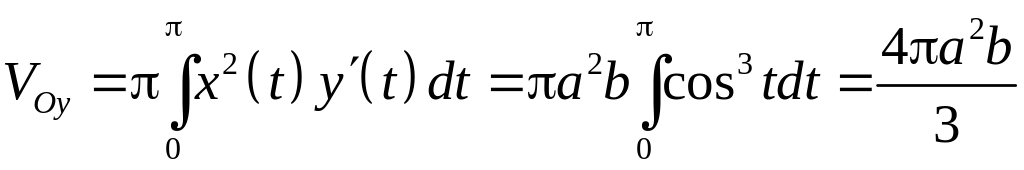
.
Обратим внимание,
что в случае шара
![]()
,
его объем равен
![]()
.
6.2.3. Вычислить
объем тела, образованного вращением
астроиды
вокруг оси абсцисс.
n
Используя параметрическое представление
,
при изменении параметра
в пределах от
до
,
получаем:
![]()
, ![]()
,
а объем тела равен
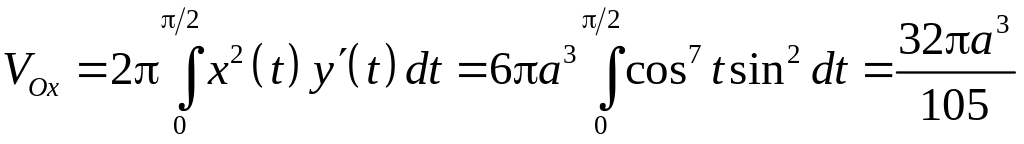
.
6.3. Вычисление длины дуги кривой
Если плоская кривая
задана параметрически
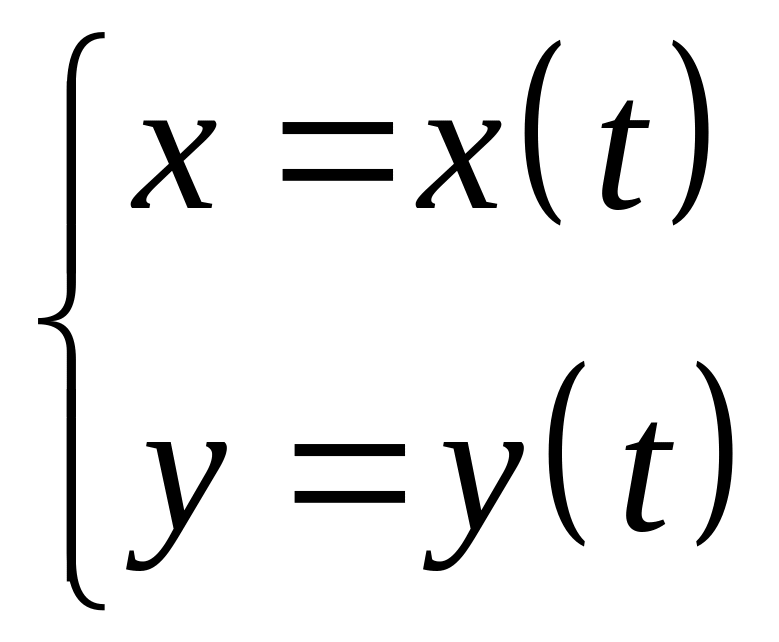
,
![]()
,
причем
![]()
и
![]()
– непрерывно дифференцируемые функции,
то она имеет длину, вычисляемую по
следующей формуле
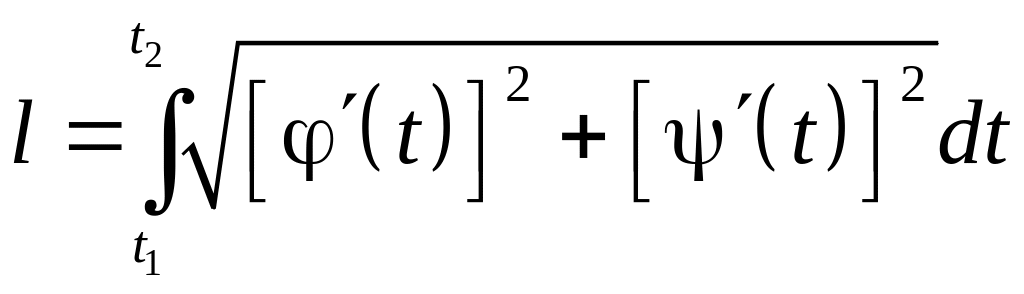
.
Если плоская кривая
– график непрерывно дифференцируемой
функции
![]()
и
![]()
,
то длина этой кривой вычисляется по
формуле
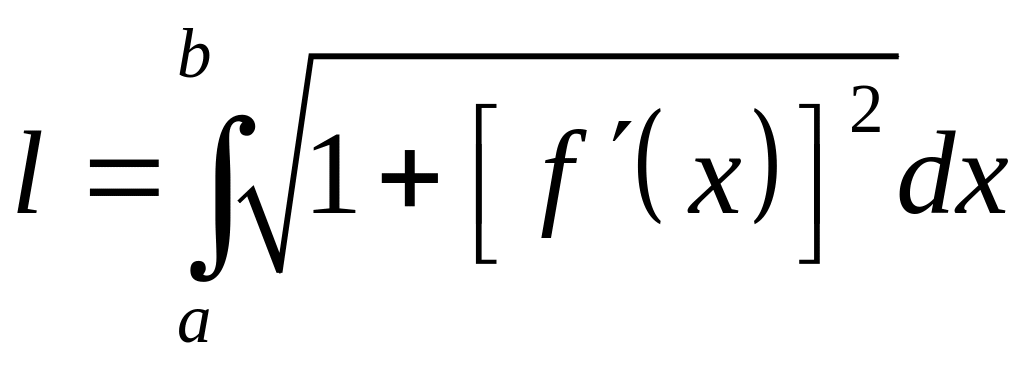
.
В полярных
координатах
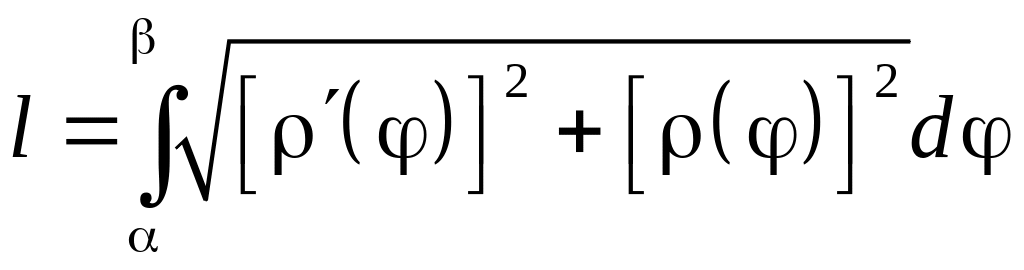
.
Пусть задана дуга
кривой
![]()
и функции
![]()
непрерывно дифференцируемы на
![]()
,
то дифференциал функции длины дуги
![]()
называется дифференциалом дуги и
вычисляется по одной из формул:
![]()
,
![]()
,
![]()
.
Примеры:
6.3.1.
Вычислить длину линии
![]()
от
![]()
до
![]()
.
n
Так как
![]()
,
то искомая длина равна
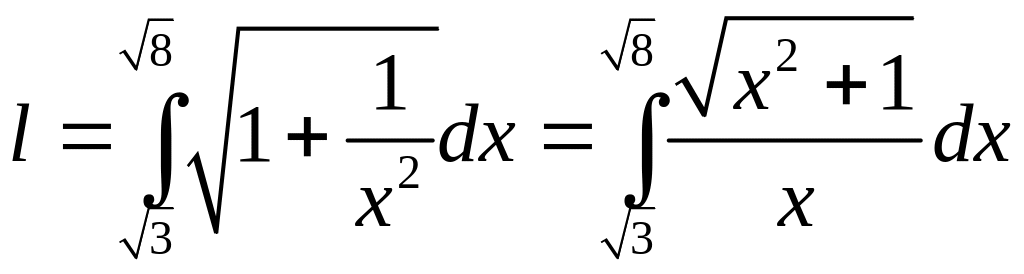
.
Положим
![]()
,
отсюда
![]()
,
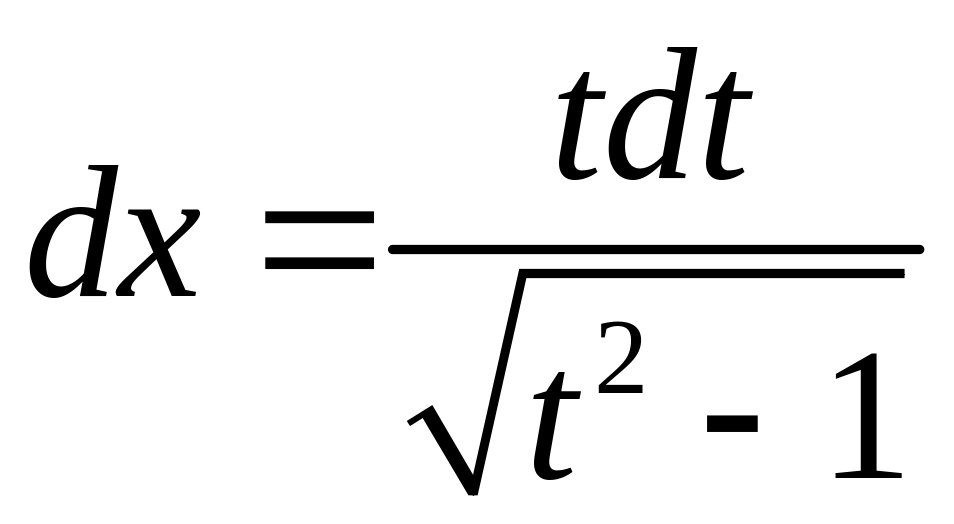
.
Новые пределы интегрирования:
![]()
,
![]()
.
Тогда:
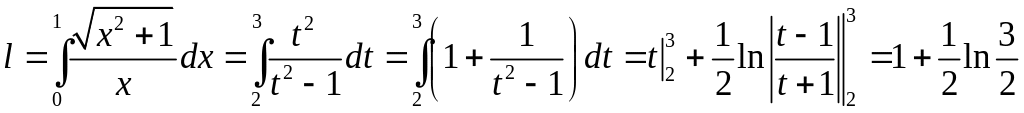
6.3.2. Вычислить
длину астроиды, заданной уравнением
(
,
).
n
Используя параметрическое представление
при изменении параметра
в пределах от
до
(первая четверть) и находя производные
![]()
и ![]()
,
Получаем
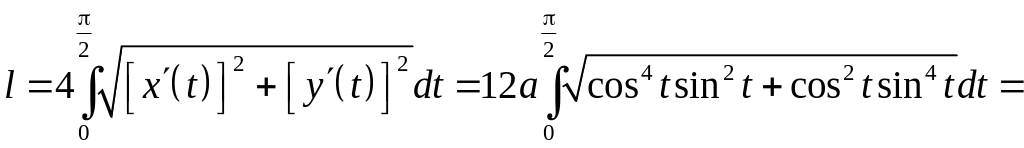
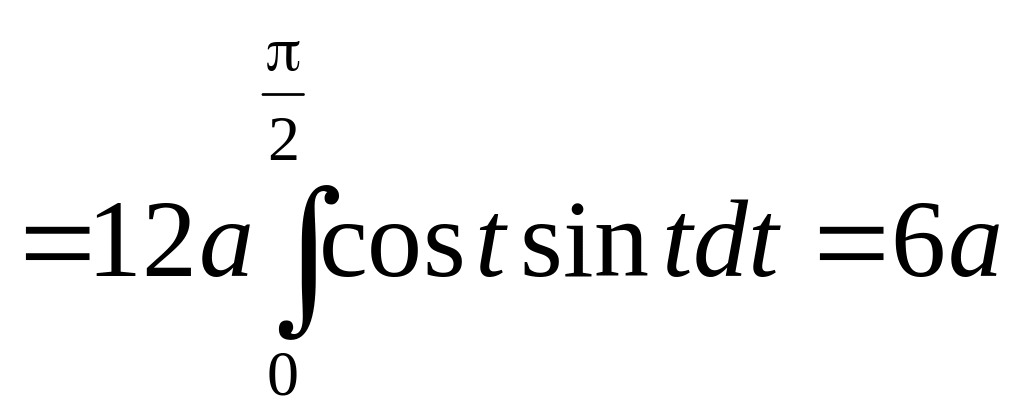
.
6.3.3.
Вычислить
длину кардиоиды,
заданной уравнением
.
n
Так как
![]()
,
то
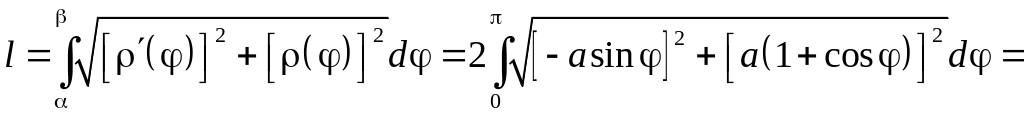
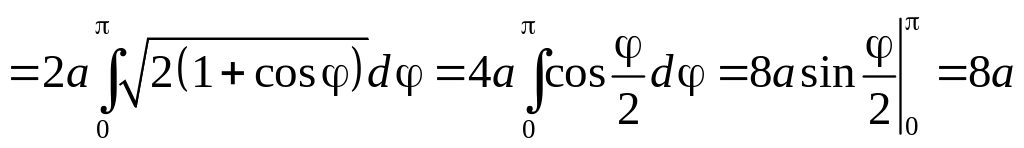
.
6.4. Вычисление площади поверхности вращения
Пусть задана
кривая
,
и прямая
![]()
,
являющаяся осью вращения. Тогда площадь
поверхности
![]()
полученная вращением
вокруг оси
вычисляется
по формуле
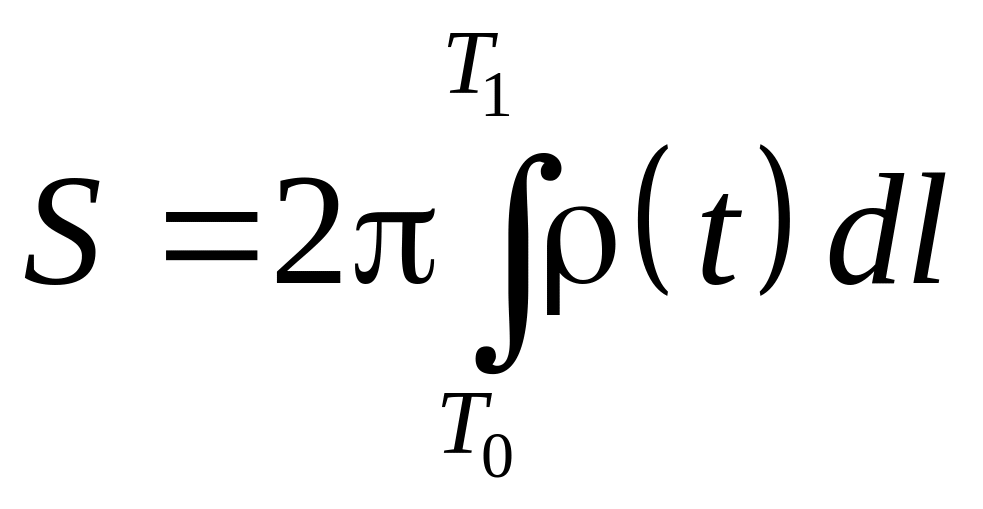
,
где
![]()
– расстояние от точки
![]()
,
лежащей на кривой
,
до оси вращения
,
а
![]()
– дифференциал дуги
.
То есть если
поверхность:
а) получается при
вращении кривой
,
вокруг оси
,
то в качестве параметра вводится
переменная
![]()
,
![]()
,
и искомая площадь равна

.
б) получается при
вращении параметрически заданной кривой
![]()
вокруг оси
,
то
![]()
,
,
а её площадь равна
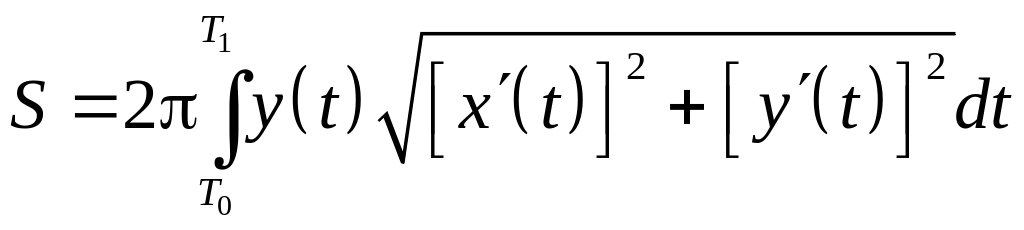
.
в) получается при
вращении кривой заданной в полярных
координатах
![]()
вокруг полярной оси, то
![]()
,
,
площадь находится по формуле

.
Примеры:
6.4.1. Вычислить
площадь поверхности, образованной
вращением астроиды, заданной уравнениями
,
вокруг оси абсцисс.
n
Так как
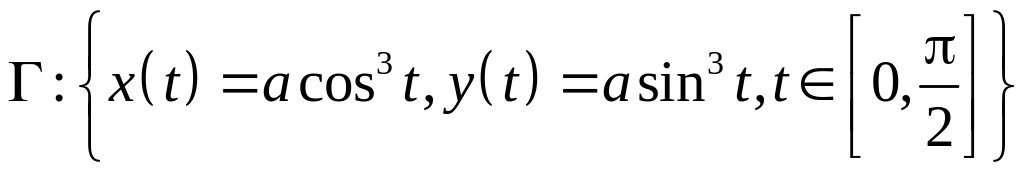
,
![]()
,
![]()
то площадь
поверхности, получаемой при вращении
астроиды равна
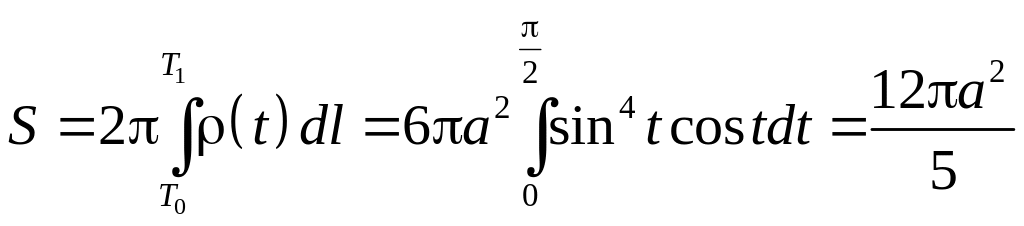
6.4.2. Вычислить
площадь поверхности получаемой вращением
цепной линии
![]()
(такая поверхность называется катеноидом)
вокруг оси абсцисс и ограниченного
двумя плоскостями
и
,
перпендикулярными оси абсцисс.
n
Напомним, что
![]()
,
![]()
,
![]()
![]()
, ![]()
.
Тогда площадь
поверхности катеноида будет равна
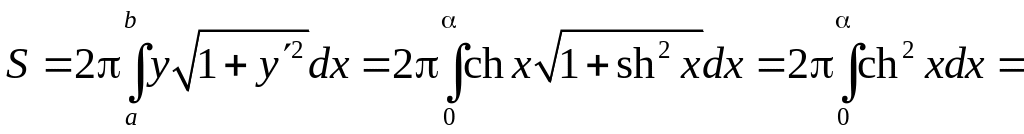
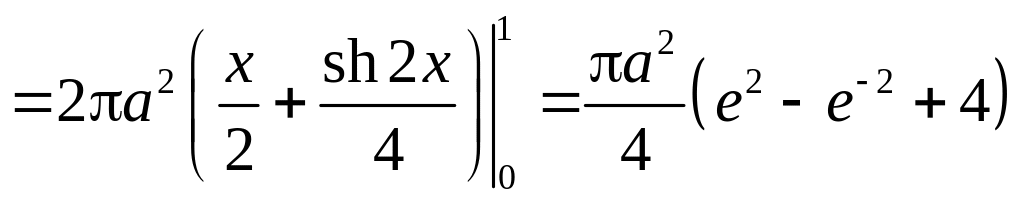
.
6.4.3. Найти
площадь поверхности вращения удлиненного
и укороченного эллипсоида (см. задачу
6.2.2.).
n
Используем параметрическое параметрическое
представление эллипса
,
.
Вычисляя производные
,
.
Тогда, при изменении
от
до
,
получаем для удлиненного эллипсоида
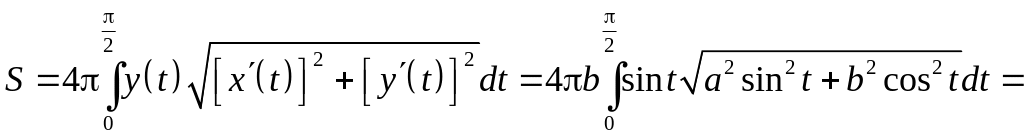
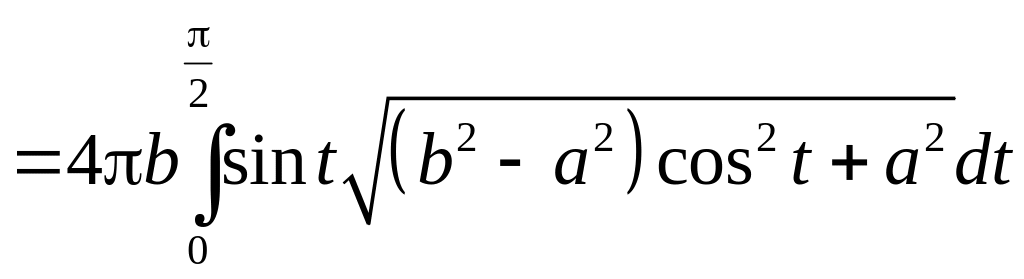
Обозначая

– эксцентриситет эллипса, получаем:
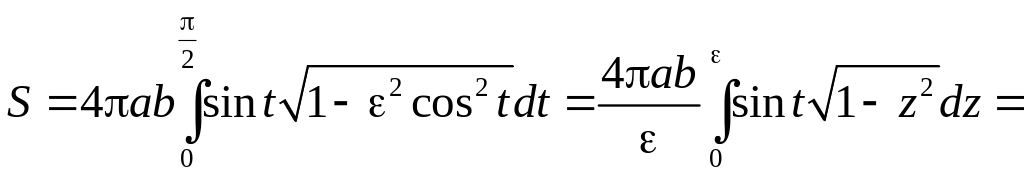
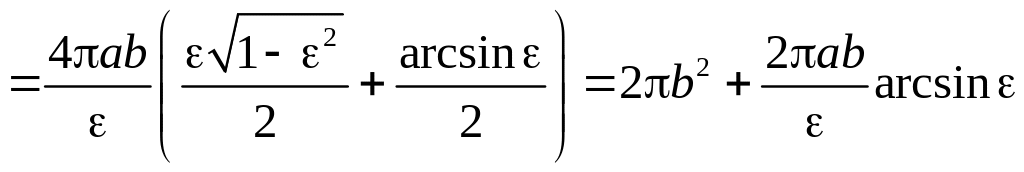
.
Аналогично, для
укороченного эллипсоида
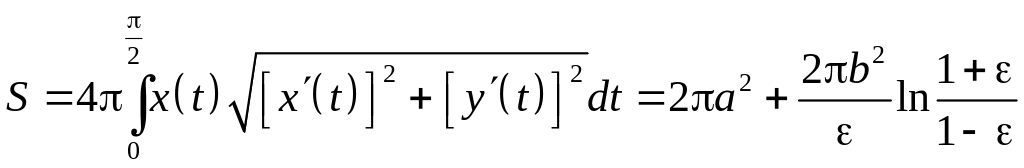
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
I. Объемы тел вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п°п° 197, 198* Разберите подробно примеры, приведенные в п° 198.
508. Вычислить объем тела, образуемого вращением эллипса Вокруг оси Ох.
Вокруг оси Ох.
Решение. При вращении эллипса вокруг оси Ox образуется тело, называемое эллипсоидом вращении. Как известно, объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху кривой у = f{x), ординатами х = а, х = Ь и осью Ох, вычисляется по формуле:

Из уравнения эллипса видно, что большая его полуось равна 2, следовательно, . Разрешив уравнение
. Разрешив уравнение
эллипса относительно , получим
, получим Объем
Объем
эллипсоида вращения равен:

509. Найти объем тора, образованного вращением круга
 Вокруг оси Ox (рис. 18). Решение. Искомый объем тора равен разности объемов, полученных от вращения верхнего и нижнего полукругов. Так как для верхнего полукруга
Вокруг оси Ox (рис. 18). Решение. Искомый объем тора равен разности объемов, полученных от вращения верхнего и нижнего полукругов. Так как для верхнего полукруга
 , а для нижнего
, а для нижнего , то
, то

(см. задачу 388).
Б10. Вычислить объем прямого конуса, высота которого h и радиус основания г, рассматривая конус как тело вращения прямоугольного треугольника около одного из катетов.
Решение. Выберем систему координат так, чтобы ось Ox совпала с высотой h (рис. 19), а вершину конуса

примем за начало координат. Тогда уравнение прямой OA

Следовательно, объем конуса
запишется так: будет равен:

511. Вычислить объемы тел, образованных вращением около осей Ox и Oy сегмента AOB параболы , от
, от
секаемого хордой AFB, проходящей через фокус параболы перпендикулярно к оси Ox (рис. 20, а, б).
Решение I. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Ох, пользуясь формулой:
Найдем пределы интегрирования. Прямая AB параллельна оси Oy. Ее уравнение . Для того чтобы
. Для того чтобы
найти точки пересечения этой прямой с параболой, решим совместно систему уравнений:

мя я AB проходит через фокус параболы, то координаты точки F будут Следовательно,
Следовательно,


Получим точки . Так Kaw пря
. Так Kaw пря
2. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Oy. Учитывая симметрию сегмента относительно оси Oxi найдем сначала половину искомого объема. Она равна разности объемов тел, получаемых от вращения вокруг оси Oy прямоугольника OFBD и криволинейного тоеугольника OBD. Так как объем цилиндра равен , а объем
, а объем Тела, полученного от вращения криволинейного треугольника OBD вокруг оси Oy, будет:
Тела, полученного от вращения криволинейного треугольника OBD вокруг оси Oy, будет:
512. Фигура, ограниченная гиперболой И
И

то половина искомого объема равна:

Следовательно, весь искомый объем

прямыми , вращается вокруг оси
, вращается вокруг оси
Ох. Найти объем тела вращения.
Решение. В результате вращения данной фигуры вокруг оси Ox образуются два тела вращения, имеющие равные объемы Тогда
Тогда
Найдем объем V1 тела (рис. 21), сбразованного вращением площади, ограниченной правей ветвью гиперболы  И прямей
И прямей Пределы интегрирова
Пределы интегрирова
ния найдем из геометрических соображений:
 . Таким образом,
. Таким образом, 
513. Вычислить объем тела, образованного вращением вокруг оси Ox одной полуволны синусоиды у = sin х.
514. Найти объем конуса, производимого вращением вокруг оси Ox части прямой _ , содержащейся между осями координат.
, содержащейся между осями координат.
515. Криволинейная трапеция, ограниченная срерху параболой ,с боков—ординатами х = — I и х—, снизу — осью Ох, вращается вокруг оси Ох. Найти объем полученного тела вращения.
,с боков—ординатами х = — I и х—, снизу — осью Ох, вращается вокруг оси Ох. Найти объем полученного тела вращения.
516. Вычислить объем тела, образованного вращением вокруг оси Ox площади, ограниченной цепной линией
 , ординатами X = — а, х = а и осью Ох.
, ординатами X = — а, х = а и осью Ох.
517. Прямой параболический сегмент, основание которого а, а высота R, вращается вокруг основания. Определить объем полученного тела вращения.
518. Найти объем цирка, осевое сечение которого — парабола. Высота цирка 30 м. Диаметр основания 50 м.
519. Найти объем тела, образованного вращением кривой Вокруг оси абсцисс.
Вокруг оси абсцисс.
520. Вычислить объем тела, полученного вращением
астроиды Вокруг оси Oy.
Вокруг оси Oy.
521. На кривой Взяты две точки А и В, абсциссы которых соответственно а = I и Ь = 2. Найти объем тела, полученного вращением криволинейной трапеции аАВЬ вокруг оси Ох.
Взяты две точки А и В, абсциссы которых соответственно а = I и Ь = 2. Найти объем тела, полученного вращением криволинейной трапеции аАВЬ вокруг оси Ох.
522. Найти объем тела, производимого вращением площади, ограниченной дугой циклоиды ,
,
 И осью Ox вокруг ее основания.
И осью Ox вокруг ее основания.
523. Вычислить объем тела, образованного вращением вокруг оси ординат дуги OM циклоиды ,
,
 , ограниченной точками О (0, 0) и M (та*, 2а).
, ограниченной точками О (0, 0) и M (та*, 2а).
524. Найти объем тела, ограниченного поверхностью, полученной при вращении линии
вокруг оси абсцисс.
2. Площадь поверхности тела вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 205. В теоретическом курсе показано, что площадь поверхности тела вращения определяется по формуле:

52$. Определить площадь поверхности параболоида, образованного вращением дуги параболы у2 = 2х вокруг оси Ox от х = 0 до х = 2.
Решение. В нашем случае . Поэтому
. Поэтому

526. Найти площадь поверхности шара радиуса R. Решение. Поместим начало координат в центре шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружности Вокруг оси Ох. Тогда площадь поверхности шара найдется по формуле:
Вокруг оси Ох. Тогда площадь поверхности шара найдется по формуле:

T ак как
 И, следовательно,
И, следовательно,


527. Найти площадь поверхности эллипсоида, образованного вращением эллипса Вокруг оси Ох.
Вокруг оси Ох.
Решение. Из уравнения эллипса имеем:
 . Найдем производную:
. Найдем производную:
Тогда . Так как полуось эллипса
. Так как полуось эллипса
 И, следовательно,
И, следовательно,

Если кривая задана параметрически, то, заменяя переменную под знаком определенного интеграла, получим для площади поверхности следующую формулу:

528 Вычислить площадь поверхности, сбразованной вращением одной арки циклоиды

 Вокруг оси Ox (см. рис. 13).
Вокруг оси Ox (см. рис. 13).
Решение. Найдем:

Тогда . Искомая по
. Искомая по
верхность равна:

Решение. Построим данную кривую. Найдем точки пересечения ее с осями координат.


нием петли кривой х = /2, у
(/2— 3) вокруг оси Ох.
При у — 0 находим t = 0 и t = ±}/ 3 . Следовательно, X1 = 0 и X2 -= 3* т. е. кривая пересекает ось Ox в двух точках О (0, 0) и А (3, 0).
При х = 0 находим / = 0, следовательно, у = 0. Мы получили ту же точку О (0, 0).
При люб dx вещественных значениях параметра / будут вещественны х и у Так как х — четная функция параметра /, у — нечетная функция параметра /, то график расположен симметрично относительно оси Ох.
Исследуем данную функцию на экстремум. Находим производную:

dy = /2-dx 21

Легко видеть, что у = 0 при / = + I и, следовательно^

У

у — + —; когда X= I; у’-* оо, когда / —> 0, следовательно,
когда х -> 0, то и у 0. Это значит, что в начале координат касательная к данной кривой вертикальна. В точке

А (3; 0) будет у’ = – J=, это значит, что касательная У з
к данной кривой в этой точке образует с положительным направлением оси Ox угол в 30°.

Полученных данных достаточно для построения графика данной функции (рис. 22).
Найдем площадь данной поверхности. Имеем: х’ = 21, y’ = f – I; х’% -(-y’z = (I +12 )а.

З о
Таким образом,

Р=2* Jyj/T^T |±(<*_3)(1+/«)Л =
0 KT
IrF ^ з
3 Ik 2 2 2 /
530. Найти площадь поверхности, образованной вращением вокруг оси Ox дуги синусоиды у = sin х от точки X = 0 до точки X = It.

531. Вычислить площадь поверхности конуса с высотой h и радиусом г.
532. Вычислить площадь поверхности, образованной

2_ 2_ 2_
вращением астроиды х3 -)- у* — а3 вокруг оси Ох.
533. Вычислить площадь поверхности, образованной цращением петли кривой 18 уг — х (6 — х)г вокруг оси Ох.

534. Найти поверхность тора, производимого вращением круга X2 – j – (у—З)2 = 4 вокруг оси Ох.

535. Вычислить площадь поверхности, образованной вращением окружности X = a cost, y = asint вокруг оси Ох.

536. Вычислить площадь поверхности, образованной вращением петли кривой х = 9t2, у = St — 9t3 вокруг оси Ох.

537. Найти площадь поверхности, образованной вращением дуги кривой х = е*sint, у = el cost вокруг оси Ox


от t = 0 до t = —.
2
538. Показать, что поверхность, производимая вращением дуги циклоиды х = a (q> —sin ф), у = а (I — cos ф) вокруг оси Oy, равна 16 и2 о2.


539. Найти поверхность, полученную вращением кардиоиды Вокруг полярной оси.
Вокруг полярной оси.
540. Найти площадь поверхности, образованной вращением лемнискаты Вокруг полярной оси.
Вокруг полярной оси.
Дополнительные задачи к главе IV
Площади плоских фигур
541. Найтивсю площадь области, ограниченной кривой И осью Ох.
И осью Ох.
542. Найти площадь области, ограниченной кривой
 И осью Ох.
И осью Ох.
543. Найти часть площади области, расположенной в первом квадранте и ограниченной кривой
л осями координат.
544. Найти площадь области, содержащейся внутри
петли:
545. Найти площадь области, ограниченной одной петлей кривой:
546. Найти площадь области, содержащейся внутри петли:
547. Найти площадь области, ограниченной кривой
 И осью Ох.
И осью Ох.
548. Найти площадь области, ограниченной кривой
 И осью Ох.
И осью Ох.
549. Найти площадь области, ограниченной осью Oxr
прямой И кривой
И кривой
550. Найти площадь области, ограниченной кривыми.
 И осью Oy.
И осью Oy.
Вычисление длины дуги
551. Найти длину дуги кривой От точки А(0: до точки В (I: 6).
От точки А(0: до точки В (I: 6).
552. Найти длину дуги CD кривой , где
, где
 Дать геометрическую иллюстрацию.
Дать геометрическую иллюстрацию.
553. Найти длину дуги OA кривой Где
Где

554. Найти длину дуги AB кривой у = еху где А (0; I), В (I; 2)
555. Нгйти длину дуги AB кривой , где
, где

556. Нгйти длину дуги кривой , отсеченной прямей X = — I.
, отсеченной прямей X = — I.
557. Нгйти длину дуги кривой От
От
 До
До
Объем тела вращения
558. Нгйти объем тела, полученного вращением вокруг юси Ox п/ощоди, сграниченной крквой
559. Нййти объем тела, полученного от вращения рокруг сси Ox площади, ограниченной кривой
560. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченной кривой
ц прямыми
561. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченней эллипсом
562. Нгйти объем тела, полученного вращением вокруг оси Oy плещади, ограниченной кривой
 И отрезком оси Oy.
И отрезком оси Oy.
563. Найти объем тела, полученного вращением вокруг оси Ox площади, ограниченной кривой
564. Круг радиуса 2 с центром в точке (7; 0) вращается вокруг оси Oy. Определить объем полученного тела вращения.
565. Нлйти объем тела, полученного вращением вокруг оси Ox площади, расположенной в первом квадранте и
ограниченной кривой (эволюта
(эволюта
эллипса).
Площадь поверхности вращения
566. Найти площадь поверхности, образованной вращением дуги кривой , отсеченной прямой
, отсеченной прямой
567. Найти площадь поверхности шаоовой чаши, полученной при вращении круга Вокруг оси Ox в пределах от 0 до h.
Вокруг оси Ox в пределах от 0 до h.
568. Найти площадь поверхности катеноида, образованного вращением вокруг оси абсцисс цепной линии
 От точки
От точки До точки
До точки
569. Найти площадь поверхности эллипсоида, образованного вращением эллипса Вокруг оси Oy.
Вокруг оси Oy.
570. Найти площадь поверхности, образованной вращением вокруг оси Ox петли кривой
571. Найти площадь поверхности, образованной вращением вокруг оси Ox кривой
572. Найти площадь поверхности, образованной вращением Вокруг полярной оси.
Вокруг полярной оси.
ПРИЛОЖЕНИЯ К ВОПРОСАМ ФИЗИКИ
| < Предыдущая | Следующая > |
|---|
Содержание:
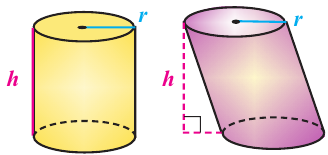
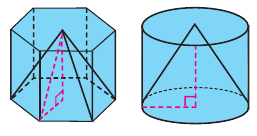
Говоря об объеме, имеют ввиду вместимость пространственной фигуры. Как вы думаете, емкость какого из цилиндров на рисунке больше?

Призмой, вписанной (описанной) в цилиндр, называется призма, основания которой вписаны (описаны) в основания цилиндра.
Объем цилиндра
Пусть в цилиндр с радиусом 
При бесконечном возрастании 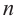 площадь оснований данных призм приближаются к площади основания
площадь оснований данных призм приближаются к площади основания 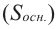 цилиндра, а их объемы к объему цилиндра:
цилиндра, а их объемы к объему цилиндра:
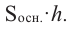
Объем цилиндра равен произведению площади основания на высоту.
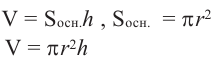
Практическая работа. Какая связь существует между объемами призмы и пирамиды, если они имеют одинаковые высоты и основания? Можно ли эту связь применить для объемов цилиндра и конуса?
Сделайте из картона модели сосудов в виде конуса и цилиндра, радиусы оснований и высоты которых одинаковы. Заполните цилиндрический сосуд при помощи сосуда в виде конуса (песком, рисом, и т. п.).
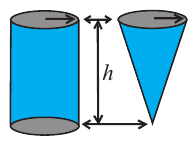
Сколько таких сосудов понадобится, чтобы заполнить цилиндрический сосуд? Верно ли утверждение, что цилиндрический сосуд можно заполнить тремя полными сосудами в виде конуса?
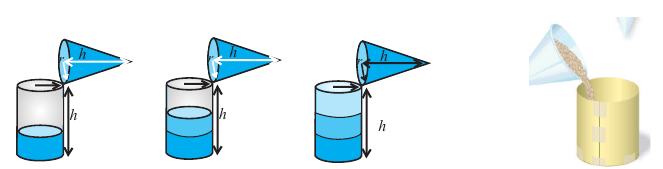
Обобщите соответствующую информацию о вычислении объема призмы, цилиндра, пирамиды и конуса, записав ответ в закрашенные ячейки.
Объем призмы и цилиндра:
Объем = площадь основания 
Объем пирамиды и конуса:
Объем =  объем призмы или цилиндра, имеющих одинаковые
объем призмы или цилиндра, имеющих одинаковые
основание и высоту.
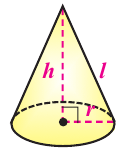
Объем конуса
Объем конуса равен произведению одной третьей площади основания на высоту.
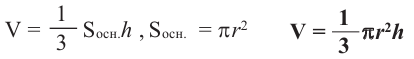
Пример №1
Образующая конуса 9 см, высота 6 см. Найдите объем конуса.
Решение:
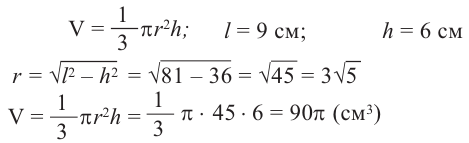
Объем шара и его частей
Практическая работа.
1. Возьмите мяч. Определите его диаметр.
2. Изобразите на бумаге развертку цилиндра, диаметр и высота которого равны диаметру шару.
3. Вырежьте и сверните полученную развертку в цилиндр без верхней крышки. Скрепите развертку при помощи клейкой ленты. Разделите высоту цилиндра на 3 равные части и сделайте соответствующие разметки.

4. Обверните мяч фольгой или плотным материалом и сделайте мешок сферической формы. Наполните его песком.

5. Пересыпьте песок в цилиндр. Какая часть цилиндра заполнится?
Если разделить поверхность шара сеткой из вертикальных и горизонтальных линий и маленький “прямоугольный” кусочек сферы соединить с центром шара, то можно представить, что шар состоит из множества “маленьких пирамид”.

Объем шара можно выразить через сумму объемов “маленьких пирамид” 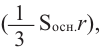 высота которых равна радиусу шара. Бесконечно уменьшая размеры оснований, количество пирамид будет бесконечно расти.
высота которых равна радиусу шара. Бесконечно уменьшая размеры оснований, количество пирамид будет бесконечно расти.
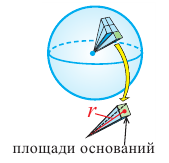
Сумма площадей оснований “маленьких пирамид” будет равна площади поверхности шара. Учитывая, что площадь поверхности шара равна 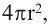 получим формулу для нахождения объема шара:
получим формулу для нахождения объема шара:
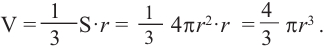
Объем шара:
Объем шара равен произведению 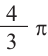 и куба радиуса.
и куба радиуса.
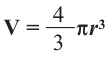
Пример №2
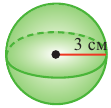
Найдите: а) объем шара радиуса 3 см
b) радиус шара объемом 288 
Решение:
а) 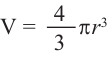
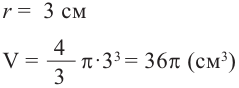
b) 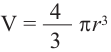

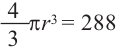
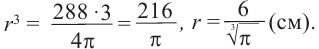
Сектор шара и сегмент шара
Шаровой сектор — это часть шара, ограниченная конической поверхностью с вершиной в центре шара. Шаровой сектор-объеденение конуса и шарового сегмента.
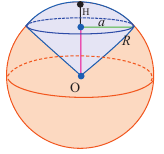
Так как шаровой сектор можно рассмотреть как предел суммы объемов маленьких пирамид, вершины которых находятся в центре шара, а основания касаются его поверхности, то
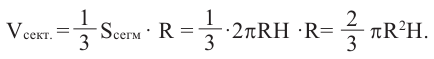
Здесь 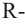 радиус шара,
радиус шара, 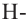 высота соответствующего сегмента
высота соответствующего сегмента
С другой стороны,
Проектная работа.
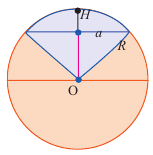
Отношение между объемами цилиндра, конуса и шара, которое получил Архимед.
Архимед нашел формулу для нахождения объема шара, исследовав связь между объемом цилиндра, описанного вокруг шара радиуса и объемом конуса, вписанного в данный цилиндр. Попробуйте и вы выполнить это исследование.

Если 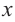 – расстояние от центра шара до плоскости сечения, то для шара радиуса
– расстояние от центра шара до плоскости сечения, то для шара радиуса 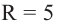 представьте зависимость площади сечения от
представьте зависимость площади сечения от 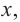 выполнив следующие шаги.
выполнив следующие шаги.
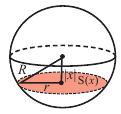
a) Вычислите следующие значения функции 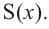
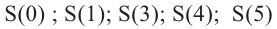
Для примера найдено значение 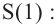
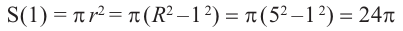
b) Представьте свои суждения о значениях 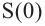 и
и 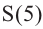 сечений.
сечений.
c) Запишите общую формулу для определения площади сечения, расположенного на расстоянии 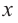 от центра шара радиуса
от центра шара радиуса 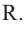
d) Свяжите формулу, полученную в пункте  и следующий рисунок.
и следующий рисунок.

e) Чтобы понять умозаключения Архимеда, вернемся к начальному рисунку.
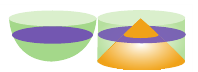
При “извлечении” конуса из цилиндра в поперечном сечении получаем кольца, параллельные основанию.
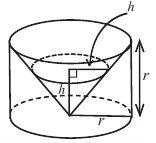
На одном и том же уровне поперечное сечение шара является кругом. Из подобия треугольников можно доказать, что площадь кольца каждого слоя равна 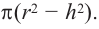 Поскольку площади этих плоских сечений равны, по принципу Кавальери равны и объемы этих тел.
Поскольку площади этих плоских сечений равны, по принципу Кавальери равны и объемы этих тел.
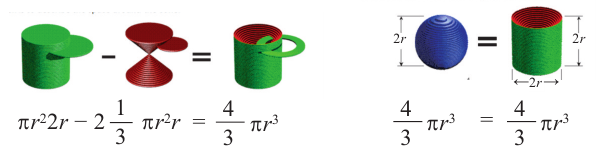
Объемы подобных фигур
Отношения соответствующих линейных размеров подобных пространствнных фигур должны быть равны.
По заданным соответствующим размерам подобных пространственных фигур можно найти неизвестные размеры.
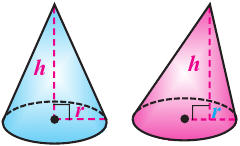
Пример №3
Конусы  и
и  подобны. По данным рисунка найдите образующую конуса
подобны. По данным рисунка найдите образующую конуса 
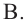
Решение: Запишем отношение линейных размеров: Радиус А Образующая А
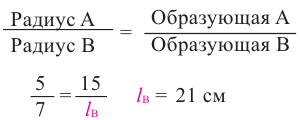
Известно, что отношение площадей поверхностей двух подобных пространственных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия:
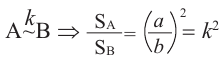
Объемы подобных пространственных фигур
Отношение объемов подобных пространственных фигур  и
и  равно кубу отношения соответствующих линейных размеров или кубу коэффициента подобия:
равно кубу отношения соответствующих линейных размеров или кубу коэффициента подобия:
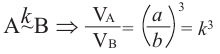
Пример №4
Отношение боковых поверхностей двух подобных цилиндров равно 4:9. Зная, что разность объемов равна 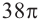 куб.ед., найдите объемы цилиндров.
куб.ед., найдите объемы цилиндров.
Решение: по условию 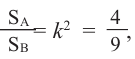 тогда
тогда 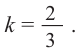 Значит
Значит 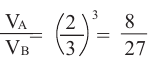 С другой стороны, принимая во внимание, что
С другой стороны, принимая во внимание, что 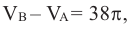 получим:
получим:
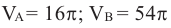
Объемы тел в высшей математике
Под телом Т будем подразумевать ограниченное множество в пространстве.
Будем рассматривать тела, имеющие внутренние точки и границу, которая также принадлежит телу (замкнутые тела), причем такие, что любые две внутренние
точки можно соединить непрерывной линией, проходящей внутри тела.
Определение 1. Рассмотрим тело 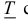 составленное из конечного числа многогранников, содержащихся в Т, и тело
составленное из конечного числа многогранников, содержащихся в Т, и тело 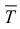 , составленное из многогранников и покрывающее тело Т:
, составленное из многогранников и покрывающее тело Т: 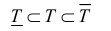
Пусть 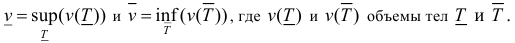 Тело называется кубируемым, если
Тело называется кубируемым, если 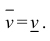 . При этом число
. При этом число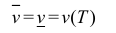 (1) называется объемом тела Т (по Жордану).
(1) называется объемом тела Т (по Жордану).
Замечание. Для кубируемости тела Т необходимо и достаточно, чтобы 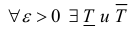 такие, что
такие, что 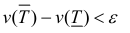 (2)
(2)
Пусть для кубируемого тела Т известны площади s=s(x) его сечения плоскостями перпендикулярными оси Ох, проходящими через точки (х, 0, 0),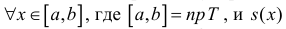 – непрерывна
– непрерывна
Разобьем отрезок [ a b ] на n частичных отрезков точками 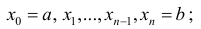
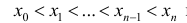 и обозначим это разбиение
и обозначим это разбиение 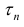 . Пусть
. Пусть 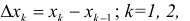
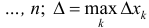 – диаметр разбиения, тогда
– диаметр разбиения, тогда 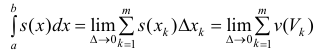 (3)
(3)
Где 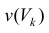 это – объем цилиндрического тела высотой
это – объем цилиндрического тела высотой 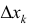 и площадью основания
и площадью основания
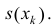 Пусть
Пусть 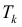 k − -ый слой тела Т между плоскостями, проходящими через точки
k − -ый слой тела Т между плоскостями, проходящими через точки 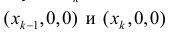 и перпендикулярными оси Ох.
и перпендикулярными оси Ох.
Так как Т – кубируемо, то 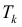 – также кубируемо и
– также кубируемо и 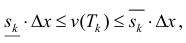 где
где
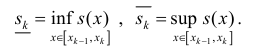
Тогда 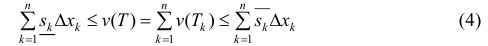
∀n ∈ N, или 
Где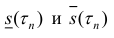 это – нижняя и верхняя суммы Дарбу функции s(x) для разбиения
это – нижняя и верхняя суммы Дарбу функции s(x) для разбиения
 Поэтому
Поэтому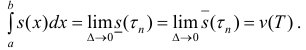 Таким образом
Таким образом 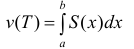 (6)
(6)
Замечание. Нужно заметить, что неравенство (4), которое использовалось для вывода формулы (6), выполняется, когда любые два рассматриваемые сечения
тела Т при проекции на плоскость yOz полностью содержатся одно в другом.
Однако формула (6) верна и в общем случае. Для этого достаточно потребовать,
чтобы тело Т было кубируемым и функция s (x) – непрерывной.
Пример №5
Найти объем тела ограниченного поверхностями 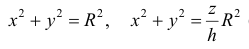 (ниже параболоида).
(ниже параболоида).
Решение.
Из системы уравнений 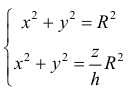 следует, что z=h.
следует, что z=h.
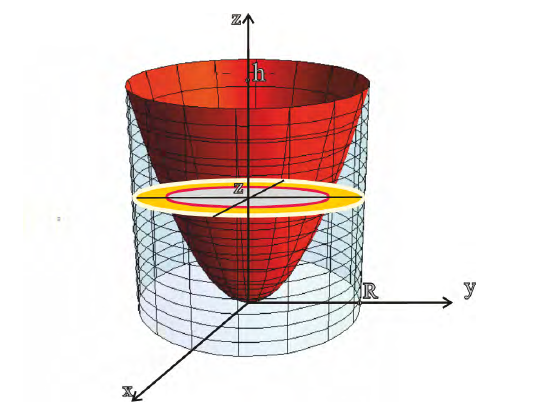
В сечении тела плоскостью проходящей через точку (0, 0, z) перпендикулярно оси Оz получается кольцо
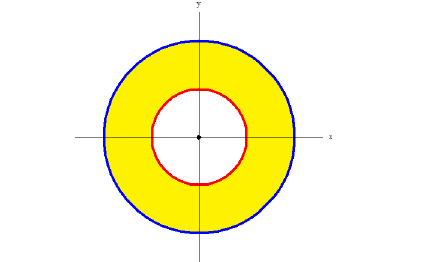
Радиус внешней окружности равен R, радиус внутренней равен 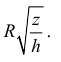
Поэтому по формуле (6):
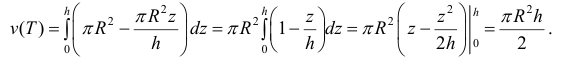
Формулу (6) удобно применять к телам вращения. Пусть y=f(x) – непрерывна на отрезке 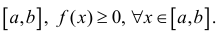 Будем вращать криволинейную трапецию
Будем вращать криволинейную трапецию
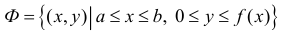
вокруг оси Ох. Получим тело:
Тогда сечением полученного тела плоскостью проходящей через точку (х,0,0) и перпендикулярной оси Ох будет круг радиуса 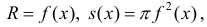 и по формуле (6):
и по формуле (6): 
Где y=f(x).
Аналогично, если 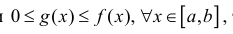 то при вращении вокруг оси Ох фигуры
то при вращении вокруг оси Ох фигуры 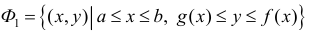
Получим тело, объем которого 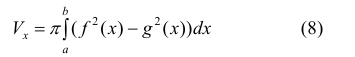
Пример №6
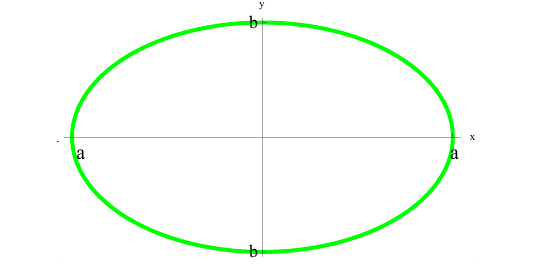
Рассмотрим фигуру Φ ограниченную эллипсом 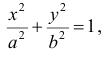
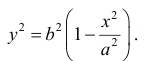
Найдем объем эллипсоида полученного при вращении вокруг оси Ох фигуры Φ .
Решение.
По формуле (7): 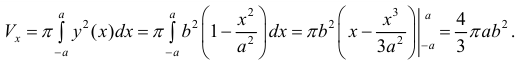
Пусть функция x=x(y) – непрерывна при 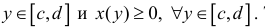 Тогда, аналогично, при вращении вокруг оси Оу фигуры
Тогда, аналогично, при вращении вокруг оси Оу фигуры 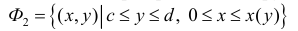
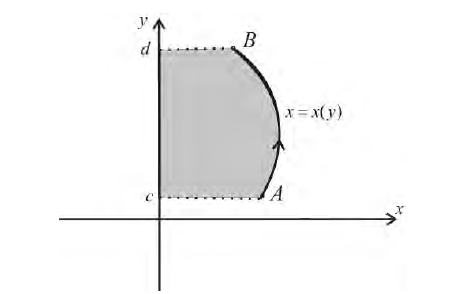
Получим тело, объем которого 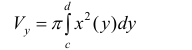 (9)
(9)
Если же вращать вокруг оси Оу трапецию 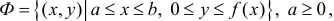
то 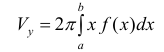 (10)
(10)
Пример №7
Рассмотрим тело Т из примера 1. Оно получается, если вращать вокруг оси Oz фигуру, ограниченную линиями:
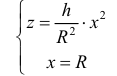
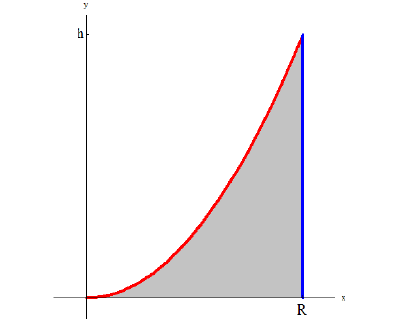
Из первого уравнения найдем 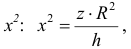 поэтому по формуле (9):
поэтому по формуле (9):
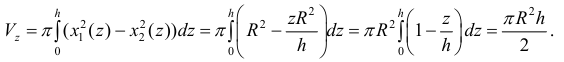
Пример №8
Объем 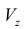 при вращении фигуры
при вращении фигуры 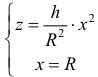 из примера 3 вокруг оси Oz можно также найти и по формуле (10):
из примера 3 вокруг оси Oz можно также найти и по формуле (10): 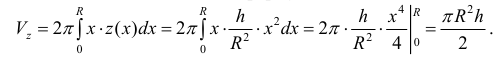
Пример №9
Фигура Ф ограничена линиями 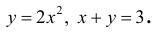 Найти
Найти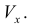
Решение.
Абсциссы точек пересечения:  (см. пример 1 § 30). По формуле (8):
(см. пример 1 § 30). По формуле (8):
Замечание. Для непрерывной функции 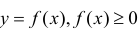 рассмотрим криволинейную трапецию
рассмотрим криволинейную трапецию 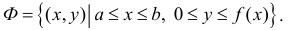
Пусть 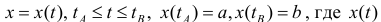 – непрерывно-дифференцируема на промежутке
– непрерывно-дифференцируема на промежутке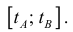 Тогда по формуле (7):
Тогда по формуле (7): 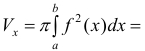 по формуле (1) § 26
по формуле (1) § 26
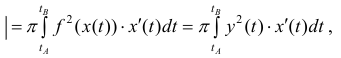
Где 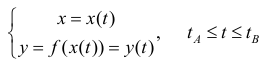 – параметрическое задание линии
– параметрическое задание линии 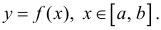 Таким образом
Таким образом 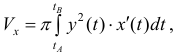 или
или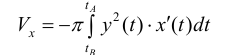 (12)
(12)
(кривая обходится так, чтобы область Ф оставалась слева).
Аналогично, для непрерывной функции 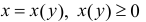 рассмотрим криволинейную трапецию
рассмотрим криволинейную трапецию 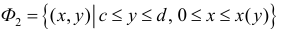
Пусть  – непрерывно-дифференцируема на промежутке
– непрерывно-дифференцируема на промежутке  Тогда по формуле (9):
Тогда по формуле (9): 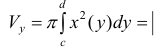 по формуле (1) § 26
по формуле (1) § 26
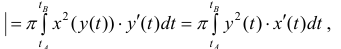
Где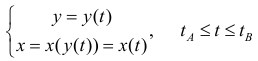 – параметрическое задание линии
– параметрическое задание линии 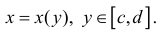
Таким образом 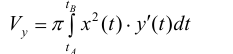 (13) (кривая обходится так, чтобы область Ф оставалась слева).
(13) (кривая обходится так, чтобы область Ф оставалась слева).
Рассмотрим область ,ограниченную простой замкнутой кривой
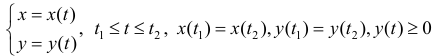 (кривая лежит по одну сторону от оси Ox ). Тогда объем
(кривая лежит по одну сторону от оси Ox ). Тогда объем  можно находить по формуле (12):
можно находить по формуле (12): 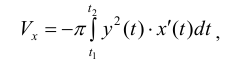
(кривая обходится так, чтобы область оставалась слева).
Аналогично ,для области ограниченной простой замкнутой кривой
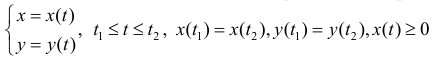 (кривая лежит по одну сторону от оси Oy )объем
(кривая лежит по одну сторону от оси Oy )объем 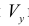 можно находить по формуле (13):
можно находить по формуле (13): 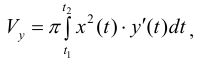 (кривая обходится так, чтобы область оставалась слева).
(кривая обходится так, чтобы область оставалась слева).
Пример №10
Дана астроида 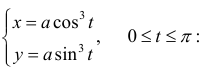
Найдем  .
.
Решение.
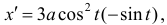 по формуле (12):
по формуле (12):
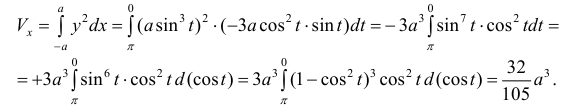
Пример №11
Петля кривой  вращается вокруг оси Ox .Найти
вращается вокруг оси Ox .Найти  .
.
Решение.
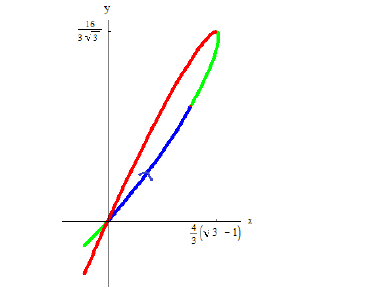
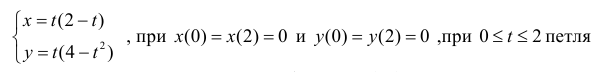 петля обходится против часовой стрелки. По формуле (12):
петля обходится против часовой стрелки. По формуле (12):
Пусть 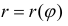 – кривая в полярной системе координат, r (ϕ) – непрерывна при
– кривая в полярной системе координат, r (ϕ) – непрерывна при 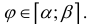 Рассмотрим на плоскости хОу криволинейный сектор
Рассмотрим на плоскости хОу криволинейный сектор
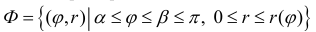
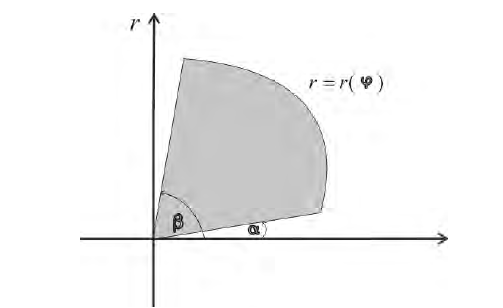
Тогда объем тела при вращении фигуры ϕ вокруг полярной оси равен
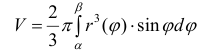 (14)
(14)
Пример №12
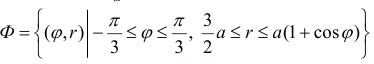 (см. пример 4 § 31).
(см. пример 4 § 31).
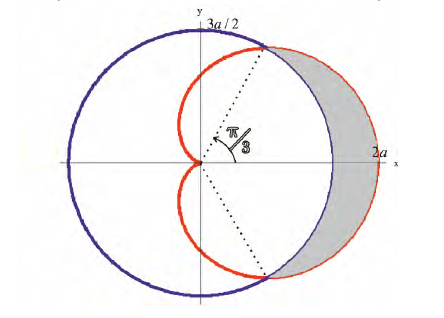
Найдем  .
.
Решение.
По формуле (14):
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Основные фигуры геометрии и их расположение в пространстве
- Пространственные фигуры – виды, изображения, свойства
- Площадь прямоугольника
- Объем пространственных фигур
- Объёмы поверхностей геометрических тел
- Фигуры вращения: цилиндр, конус, шар
