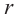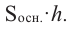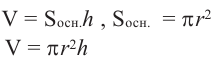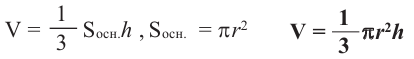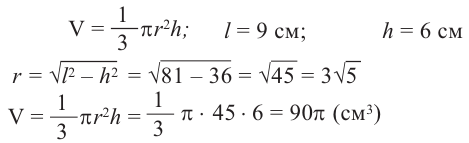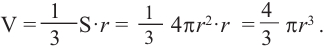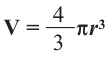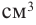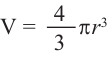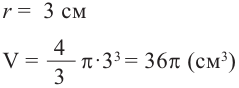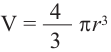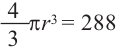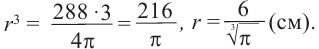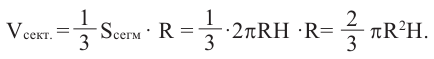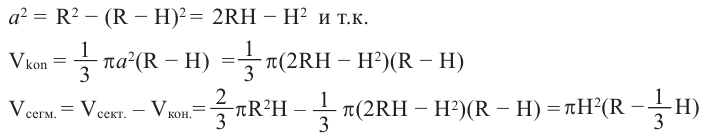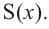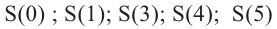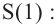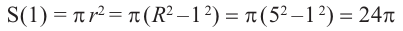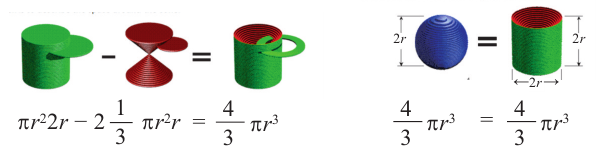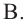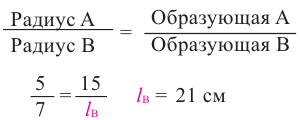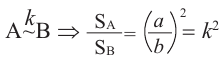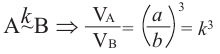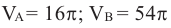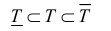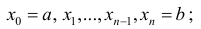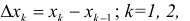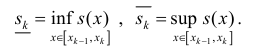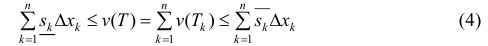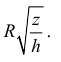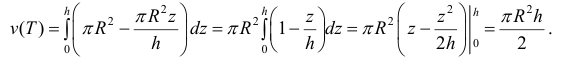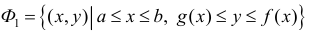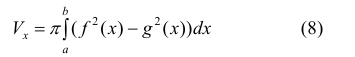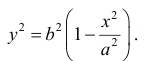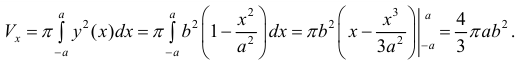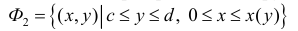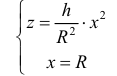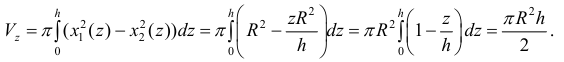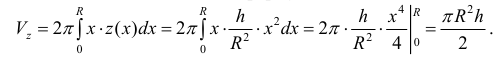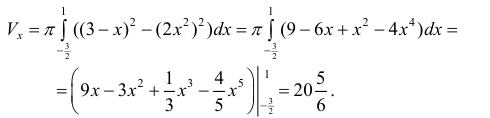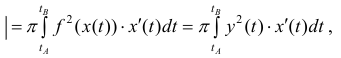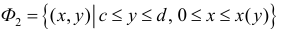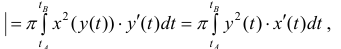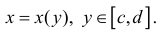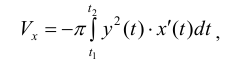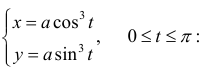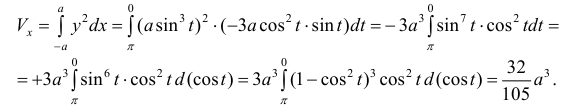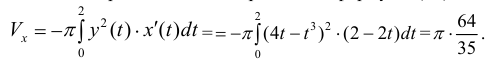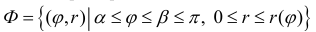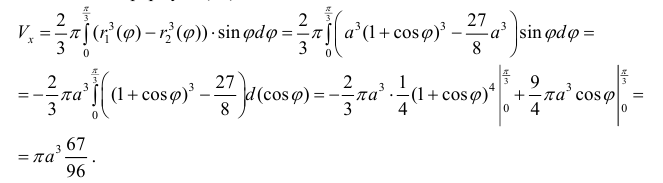Как найти объем тела вращения конуса

Дополнения

1.О применении определённого интеграла для нахождения объёмов тел вращения

1.1.Формула объёма тела вращения

В п.16.2 дано определение тела вращения.

Получим формулу для вычисления объёма тела вращения, применяя интеграл, о котором вам рассказали в курсе «Алгебры и начал математического анализа».

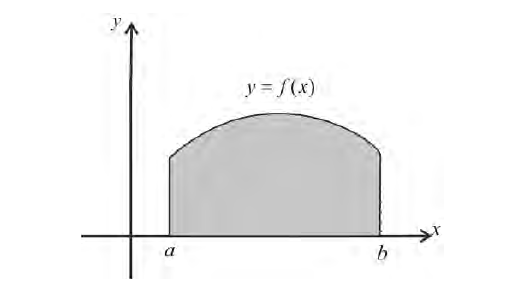
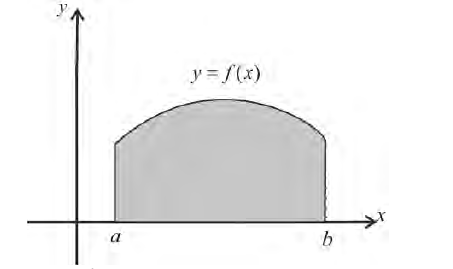
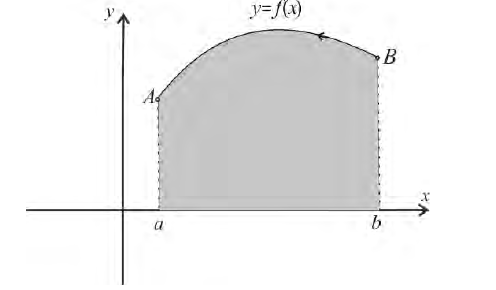
Пусть f(x) — непрерывная на отрезке [a; b] функция, не принимающая отрицательных значений; А, В — точки графика этой функции (рис. 225).

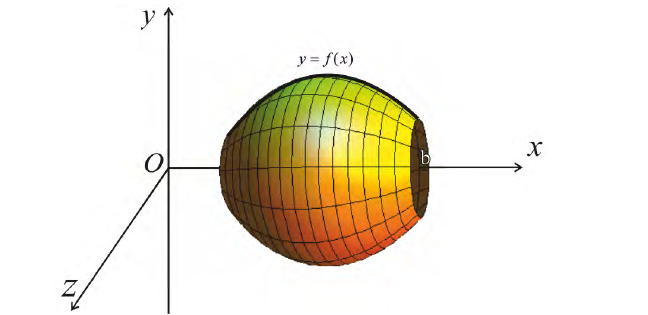
Рассмотрим криволинейную трапецию aABb, ограниченную кривой графика функции y = f(x), отрезками aA, bB и отрезком [a; b] координатной оси Ох (см. рис. 225). При вращении этой трапеции вокруг оси Ох образуется тело вращения (рис. 226), которое обозначим Ф и поставим себе задачу: найти объём этого тела.

Через произвольную точку х = с (a ⩽ с ⩽ b) отрезка [a; b] проведём плоскость, перпендикулярную оси Ox. Сечением тела Ф этой плоскостью является круг, радиус которого равен f(с), а площадь — πf2(с) (или точка (c; 0)).

Объём части тела Ф, заключённой между этой плоскостью и плоскостью х = a, изменяется при изменении x. Обозначим этот переменный объём V(х). Заметим, что V(x) = V(a) = 0 при х = a; при х = b имеем V(x) = V(b) = V — искомый объём тела вращения Ф.

Покажем, что функция V(x) имеет производную V′(х) и V′(х) = πf2(х).

Придадим абсциссе х приращение ∆х > 0, тогда объём V(х) получает приращение ∆V(х) = V(x + ∆x) – V(x). Пусть m и М — соответственно наименьшее и наибольшее значения функции f(х) на промежутке [х; х + ∆х]. Цилиндр, радиус основания которого равен m, содержится в теле вращения объёма ∆V(x), а цилиндр, радиус основания которого равен M, содержит тело объёма ∆V(х); образующие цилиндров параллельны оси Ох и имеют длину, равную ∆х. Объёмы этих цилиндров равны соответственно πm2•∆x и πM2•∆х. На основании свойства 2 объёмов (п. 10.1) получаем

πm2•∆x ⩽ ∆V(x) ⩽ πM2•∆x,

откуда

πm2 ⩽  ⩽ πM2.

Рассуждения для случая ∆х < 0 проводятся аналогично и дают тот же результат.

Пусть теперь ∆х 0. Имеем m = M = f(x), тогда

 πm2 ⩽  ⩽  πM2

или

πf2(х) ⩽  ⩽ πf2(x).

Значит,  = πf2(х). По определению производной функции  = V′(x). Поэтому V ′(x) = πf2(х), следовательно, V(х) — первообразная для πf2(х).

Таким образом, переменный объём V(x) телa вращения представляет собой одну из первообразных для функции πf 2(х) на отрезке [a; b]. Эта первообразная обладает тем свойством, что при х = a она обращается в нуль (V(a) = 0), а при х = b значение функции V(x) равно объёму тела вращения Ф (V(b) =  V).

Если F(х) — также некоторая первообразная для функции πf 2(x), то V(x) = F(x) + С, где С — произвольная постоянная. Так как V (a) = 0, то из равенства V(a) = F (a) + C = 0 находим С = –F(a). Значит, V(x) = F(x) – F(a). Toгдa V(b) = F(b) – F(a). Ho V(b) = V — искомый объём тела вращения Ф. Таким образом, V = F(b) – F(a), где F(b) и F(a) — значения первообразной для функции πf 2(х) соответственно при х = b и х = a. Это означает, что

V = f 2(x)dx = π(x)dx.

Вот почему объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = f(x), х = a, х = b, у = 0, вычисляется по формуле

V = (x)dx.(*)

ЗАДАЧА. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями у = , х = 0, x = 2 и y = 0 (рис. 227).

Решение. Воспользуемся формулой V = π(x)dx, для чего из уравнения у =   находим y2 = 2х. Тогда получаем

V = πdx = 2π• = = 4π.

Ответ: 4π.

1.2. Объёмы конуса, шара и его частей

Используя формулу V = (x)dx вычисления объёма тела вращения, получим формулы для вычисления объёма каждого изученного ранее тела вращения.

а) Объём конуса и усечённого конуса

Теорема 1 (об объёме полного конуса). Объём V конуса с высотой Н и радиусом основания R равен одной трети произведения площади основания на высоту:

V =  R2Н.

Доказательство. Конус с высотой Н и радиусом основания R можно рассматривать как тело, образованное вращением вокруг оси Ox прямоугольного треугольника с вершинами О(0; 0), А(Н; 0) и B(Н; R) (рис. 228). Треугольник АОВ является частным случаем криволинейной трапеции, которая ограничена графиком функции у =  х (0 ⩽ х ⩽ H), осью Ох и отрезком прямой х = Н. Поэтому, используя формулу (*) п. 1.1 «Дополнений» для объёма V конуса, получаем:

V = dx = π • =  πR2H,

где πR2 — площадь основания конуса. Теорема доказана. ▼

Теорема 2 (об объёме усечённого конуса). Объём усечённого конуса с высотой Н и радиусами оснований r и R равен сумме объёмов трёх конусов с высотой Н, радиусы оснований которых соответственно равны r, R и :

V =  (r2 + R2 + rR)H.

Доказательство. Усечённый конус с высотой H и радиусами оснований r и R можно получить, вращая вокруг оси Oх прямоугольную трапецию OABC, где O(0; 0), A(0; r), В(Н; R), С(H; 0) (рис. 229).

Рис. 229

Прямая AВ проходит через точки (0; r) и (Н; R), поэтому её уравнение имеет вид у =  х + r. Следовательно, трапеция ОАВС ограничена графиком функции y =  х + r (0 ⩽ х ⩽ Н), осью Oх и отрезками прямых х = 0 и х = Н. Поэтому, используя формулу (*) из п. 1.1 для объёма V усечённого конуса, получаем:

V = dx.(1)

Для вычисления интеграла сделаем замену переменных

 x + r = t.(2)

Тогда  dx = dt, откуда dx =  dt. Новые пределы интегрирования (по переменной t) найдём посредством подстановки формулы (2): х = 0 ⇒ t = r; х = Н ⇒ t = R. Таким образом, для объёма V усечённого конуса получаем:

что и требовалось доказать. ▼

б) Объём шарового слоя

В прямоугольной декартовой системе координат Оху рассмотрим криволинейную трапецию aABb, ограниченную дугой окружности х2 + у2 = R2, –R ⩽ a ⩽ х ⩽ b ⩽ R, отрезком [a; b] оси Ох и отрезками aА и bВ прямых соответственно x =  a и х = b (рис. 230, а).

Рис. 230

При вращении криволинейной трапеции aАВb вокруг оси Ох образуется шаровой слой (рис. 230, б). Найдём его объём, применяя формулу (*) п. 1.1.

Из уравнения х2 + у2 = R2 имеем у2 = R2 – x2. Поэтому для вычисления объёма V шарового слоя получаем:

Таким образом, объём шарового слоя, отсекаемого от шара x2 + y2 + z2 ⩽ R2 радиуса R плоскостями x = a и x = b, вычисляется пo формуле

V = (**)

Пусть радиусы оснований шарового слоя равны r1 и r2 (r1 > r2), а высота — H (см. рис. 230, a).

Тогда Н = b – a,  = R2 – a2,  = R2 – b2.

Формулу (**) преобразуем к виду:

Из системы равенств (b – a)2 = H2, R2 – a2 = , R2 – b2 = после почленного сложения их левых и правых частей находим:

R2 – ab = .

Тогда:

Таким образом, объём шарового слоя с радиусами оснований r1 и r2 и высотой Н вычисляется по формуле

V = .(***)

в) Объём шара

При вращении полукруга х2 + у2 = R2 (расположенного в плоскости Оху, рис. 231, а) вокруг оси Ох образуется шар радиуса R (рис. 231, б). Из уравнения окружности х2 + y2 = R2 данного полукруга имеем у2 = R2 – х2. Тогда, полагая a = –R, b = R в формуле (*) п. 1.1, находим объём V шара радиуса R:

Таким образом, имеет место следующая теорема.

Теорема 3 (об объёме шара). Объём шара радиуса R вычисляется по формуле

Vш = .

г) Объём шарового сегмента

Если b = R (см. п. 1.2, б), то получаем криволинейную трапецию aAB (рис. 232, а), при вращении которой вокруг оси Ох образуется шаровой сегмент (рис. 232, б).

Пусть высота шарового сегмента равна Н, тогда a = R – Н. Так как дуга AВ криволинейной трапеции aАВ является частью окружности x2 + y2 = R2 (в плоскости Оxу), то формулу объёма шарового сегмента получим по аналогии с выводом формулы для вычисления объёма шара, учитывая при этом, что пределы a и b интегрирования равны: a = R – H, b = R, т. е.

Таким образом, имеет место следующая теорема.

Теорема 4 (об объёме шарового сегмента). Объём шарового сегмента, отсекаемого от шара радиуса R и имеющего высоту Н, вычисляется по формуле

Vш. сегм =

Если в формуле (***) п. 1.2, б положить r2 = 0, r1 = r, то получим формулу для вычисления объёма шарового сегмента с радиусом основания r и высотой Н:

Vш. сегм =  (3r2 + H2).

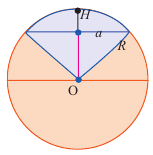
д) Объём шарового сектора

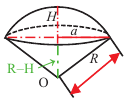
Шаровой сектор состоит из конуса с вершиной в центре шара и шарового сегмента, имеющего с конусом общее основание (риc. 233). Пусть R = ОА — радиус шара; АС = r — радиус основания шарового сегмента, NC  = H — его высота; N — точка сферы (рис. 233).

Найдём объёмы конуса и шарового сегмента, учитывая, что высота h конуса равна OC = ON – CN = R – Н.

Объём Vк конуса равен

 π•АС2•ОС =  πr2 (R – Н).

Выразим r2 через R и H.

B прямоугольном треугольнике AOC находим r2 = AC2  = ОА2 – OC2 = R2 – (R – H)2 = H(2R – H).

Значит,

Vк =  πH(2R – H)(R – H) =  (2R2 – 3RH + H2).

Для объёма шарового сегмента имеем:

Тогда для объёма шарового сектора получаем

Таким образом, доказана следующая теорема.

Теорема 5 (об объёме шарового сектора). Объём шарового сектора шара радиуса R вычисляется по формуле

Vш. сект = R2H,

где Н — длина высоты шарового сегмента, соответствующего данному шаровому сектору.

В курсе математического анализа, который вам предстоит изучать в высшей школе, будет дано строгое обоснование применения определённого интеграла не только для нахождения объёмов тел, но и для нахождения площадей поверхностей и длин дуг линий.
Решите самостоятельно следующие задачи.

1)Найдите объём тела, которое получается при вращении вокруг оси Ох криволинейной трапеции, ограниченной гиперболой у = , прямыми х = 3, х = 12 и осью абсцисс. (Ответ: 4π.)

2)Найдите объём тела, образованного вращением вокруг оси Oх фигуры, ограниченной одной полуволной синусоиды у = sin x и отрезком 0 ⩽ х ⩽ π оси абсцисс. (Ответ: 0,5π2.)

3)Найдите объём тела, полученного при вращении кривой у = 0,25х2 вокруг оси Оу в пределах от у = 1 до у = 5. (Ответ: 48π.)

4)Найдите объём тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривыми у = 2х2 и у = x3.

Формулы объема и площади поверхности. Цилиндр, конус и шар

Тела вращения, изучаемые в школе, – это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.

Например, такой важный факт:

Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем – в 8 раз. 

(ведь , ).

Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.

1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.

Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.

2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.

Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться! Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.
Мы тоже расскажем о ней.

---

План урока:

Вычисление объема тела с помощью интеграла

Вычисление объема тел вращения

Объем наклонной призмы

Объем пирамиды

Объем конуса

Объем шара

Шаровой сегмент

Площадь сферы

Вычисление объема тела с помощью интеграла

Пусть у нас есть произвольная фигура, расположенная между двумя параллельными плоскостями:

Как найти ее объем? Поступим следующим образом. Проведем прямую, перпендикулярную этим плоскостям. Эта прямая будет осью координат х. Пусть одна из плоскостей пересекает эту ось в точке а, а другая – в точке b. Таким образом, на координатной прямой появляется отрезок [a; b]. Далее разобьем этот отрезок на n равных отрезков, длина каждого из них будет равна величина ∆х. Обозначим концы этих отрезков как х₀, х₁, х₂…, х_n, причем точке х₀ будет совпадать с точкой а, а точка х_n – с точкой b. Ниже показано такое построение для n = 10:

Далее через полученные точки проведем сечения, параллельные двум плоскостям, ограничивающим фигуру. Площадь сечения, проходящую через точку с номером i, обозначим как S(x_i). Эти плоскости рассекут тело на n других тел. Обозначим объем тела, заключенного между сечениями с площадями S(x_i) и S(x_i+1) как V(x_i). Можно приближенно считать, что эти тела имеют форму прямых цилиндров (напомним, что в общем случае цилиндром необязательно считается фигура, основанием которой является круг, основание может иметь и любую другую форму). Высота всех этих цилиндров будет равна величине ∆х. Тогда объем V(x_i) может быть приближенно рассчитан так:

Общий же объем исследуемой фигуры будет суммой объемов этих прямых цилиндров:

Здесь знак ∑ означает сумму i слагаемых, каждое из которых равно величине S(x_i)•∆х. Ясно, что чем больше мы возьмем число n, тем точнее будет полученная нами формула. Поэтому будет увеличивать число n до бесконечности, тогда приближенная формула станет точной:

В правой части стоит предел суммы бесконечного числа слагаемых. Мы уже сталкивались с такими пределами, когда изучали определенный интеграл в курсе алгебры. Так как х₀ = a, а число х_n-1 при бесконечном увеличении n приближается к числу х_n, то есть к b, то можно записать следующее:

Здесь S(x) – это некоторая функция, которая устанавливает зависимость между площадью сечения объемной фигуры и координатой х, указывающей расположение этого сечения. Данная формула позволяет вычислять объем с помощью интеграла.

Итак, для вычисления объема тела необходимо:

1) выбрать в пространстве какую-то удобную ось координат Ох;

2) найти площадь произвольного сечения фигуры, проходящей перпендикулярно оси Ох через некоторую координату х;

3) найти значение чисел а и b – координат сечений, ограничивающих тело в пространстве;

4) выполнить интегрирование.

Понятно, что сразу понять, как используется эта формула, тяжело. Поэтому рассмотрим простой пример.

Задание. Фигура расположена в пространстве между двумя плоскостями, перпендикулярными оси Ох, причем координаты этих сечений равны 1 и 2. Каждое сечение фигуры с координатой х является квадратом, причем его сторона равна величине 1/х. Найдите объем тела.

Решение. В данной задаче ось Ох уже проведена. Известны и числа а и b – это 1 и 2, ведь именно плоскости, проходящие через точки х =1 и х = 2, ограничивают исследуемое тело. Теперь найдем площадь произвольного сечения с координатой х. Так как оно является квадратом со стороной 1/х, то его площадь будет квадратом этой стороны:

Вычисление объема тел вращения

Телом вращения называют тело, которое может быть получено вращением какой-то плоской фигуры относительно некоторой оси вращения. Например, цилиндр получают вращением прямоугольника вокруг одной из его сторон, а усеченный конус – вращением прямоугольной трапеции вокруг боковой стороны, перпендикулярной основанию.

В задачах на вычисление объемов таких тел ось координат Ох уже задана естественным образом – это ось вращения тела. Ясно, что каждое сечение тела, перпендикулярное оси вращения, будет являться кругом.

Рассмотрим случай, когда вокруг оси Ох поворачивают график некоторой функции у = f(x), ограниченный прямыми х = а и у = b. Тогда получится тело, сечениями которого являются круги, причем их радиусы будут равны величине f(x). Напомним, что площадь круга вычисляют по формуле:

Рассмотрим, как на практике используется эта формула.

Задание. Объемное тело получено вращением ветви параболы

вокруг оси Ох. Оно ограничено плоскостями х = 0 и х = 4. Каков объем такой фигуры?

Решение. Здесь пределами интегрирования, то есть числами а и b, будут 0 и 4. Используем формулу для тела вращения:

Объем наклонной призмы

Теперь, используя методы интегрирования, мы можем составить формулы для вычисления объема некоторых фигур. Начнем с треугольной наклонной призмы.

Пусть есть треугольная призма АВСА₂В₂С₂. Проведем ось Ох так, чтобы точка О располагалась в плоскости АВС. Пусть Ох пересечет плоскость А₂В₂С₂ в некоторой точке О₂. Тогда отрезок ОО₂ будет высотой призмы, ведь он окажется перпендикулярным к обоим основаниям.

Обозначим длину высоты ОО₂ буквой h. Далее докажем, что всякое сечение А₁В₁С₁ призмы, перпендикулярное оси Ох, будет равно ∆АВС. Действительно, если АВС⊥ОО₂ и А₁В₁С₁⊥ОО₂, то АВС||А₁В₁С₁. Прямые АВ и А₁В₁ принадлежат одной грани АВВ₂А₁, но не пересекаются, ведь они находятся в параллельных плоскостях. Аналогично АС||А₁С₁ и ВС||В₁С₁. Теперь посмотрим на четырехугольник АВВ₁А₁. АВ||A₁В₁ и АА₁||ВВ₁. Тогда АВВ₁А₁ по определению является параллелограммом. Это означает, что отрезки АВ и А₁В₁ одинаковы. Аналогично доказывается, что одинаковы отрезки АС и А₁С₁, а также ВС и В₁С₁. Но тогда одинаковы и ∆АВС и ∆А₁В₁С₁.

Итак, площади всех сечений одинаковы и равны площади основания призмы. Обозначим ее как S. Так как S не зависит от координаты, то интегрирование будет выглядеть так:

Итак, объем треугольной наклонной призмы – это произведение площади ее основания на высоту. Теперь рассмотрим произвольную призму, в чьем основании находится n-угольник. Такой n-угольник можно разбить на треугольные призмы с общей высотой h и площадями оснований S₁, S₂, S₃, …

Тогда площадь S основания всей призмы будет суммой этих чисел:

Задание. Основание призмы – это треугольник со сторонами 10, 10 и 12. Боковое ребро имеет длину 8 и образует с основанием угол в 60°. Вычислите объем призмы.

Решение. Пусть в основании призмы АВСА₁В₁С₁ лежит ∆АВС со сторонами АВ = 12 и АС = ВС = 10. Его площадь можно найти разными способами, но быстрее всего применить формулу Герона. Сначала найдем полупериметр ∆АВС:

Далее надо найти высоту призмы. Опустим из точки В₁ перпендикуляр В₁О на плоскость АВС. Тогда в прямоугольном ∆ОВВ₁ ∠В = 60° (по условию задачи и по определению угла между плоскостью и прямой). Зная длину бокового ребра ВВ₁, найдем высоту ОВ₁:

Объем пирамиды

Для начала рассмотрим треугольную пирамиду. Вершину пирамиды примем за начало координат точку О, а ось Ох проведем перпендикулярно основанию, причем ось будет направлена от вершины пирамиды к основанию.

Пусть ось Ох пересечет основание АВС в точке М. Тогда ОМ – это высота, чью длину мы обозначим как h.

Далее построим сечение А₁В₁С₁, параллельное АВС. Это сечение пересечется с ОМ в точке ОМ₁. Тогда ОМ₁ – это координата х, характеризующая расположение сечения А₁В₁С₁.

Осталось составить выражение для площади ∆А₁В₁С₁. Так как АВ||A₁B₁, то ∠АВО и ∠А₁В₁О одинаковы как соответственные углы. Тогда у ∆АВО и ∆А₁В₁О есть два равных угла (ведь ∠АОВ у них общий), а потому эти треугольники подобны по первому признаку подобия. Это означает, что

Надо как-то найти значение коэффициента k, который, очевидно, как-то зависит от переменной х. Рассмотрим теперь ∆ОМВ и ∆ОМ₁В₁. Они прямоугольные, ведь ОМ перпендикулярен плоскостям этих треугольников. Также у них есть общий угол ∠ОВМ. Значит, они подобны, и поэтому

Итак, если пирамида имеет высоту h и площадь основания S, то объем пирамиды равен:

Выведенная нами формула справедлива для треугольной пирамиды. Однако если в основании пирамиды лежит произвольный многоугольник, то, разбив этот многоугольник на треугольники, мы разобьем и пирамиду на несколько треугольных пирамид. У них будет общая высота h и площади оснований S₁, S₂, S₃…, которые в сумме составляют площадь многоугольника S.

Объем треугольных пирамид рассчитывается по выведенной нами формуле:

Задание. В основании пирамиды высотой 15 лежит квадрат со стороной 4. Вычислите ее объем.

Решение. Сначала находим площадь основания. Для этого надо сторону квадрата умножить саму на себя:

Задание. В кубе АВСDA₁В₁С₁D₁ отмечены точки Е и F – середины ребер ВС и CD соответственно. Во сколько раз объем пирамиды С₁EFC меньше объема куба?

Решение. Обозначим длину ребра куба буквой а. Тогда его объем рассчитывается так:

Задание. Отрезок MN перпендикулярен плоскости пятиугольника АВСDE. Точка K, принадлежащая этой плоскости, делит отрезок MN в отношении 2:1. Во сколько раз объем пирамиды MABCDE больше объема пирамиды NABCDE?

Решение. Запишем формулы для объемов этих пирамид. При этом учтем, что MK – высота для MABCDE, а NK – это высота для NABCDE.

Далее рассмотрим такую фигуру, как усеченная пирамида. Ясно, что ее объем можно вычислить, если из объема исходной пирамиды вычесть объем отсеченной верхушки.

Снова рассмотрим пирамиду ОАВС, через которую проведено сечение А₁В₁С₁, параллельное основанию.

Обозначим площадь нижнего основания пирамиды как S₂, а площадь верхнего основания – как S₁. Далее высоту усеченной пирамиды (отрезок ММ₁) обозначим как h. Мы уже выяснили ранее, что основания АВС и А₁В₁С₁ – это подобные треугольники, причем коэффициент их подобия k равен отношению высот ОМ и ОМ₁. Тогда можно записать:

Далее используем основное свойство пропорции:

Далее числитель дроби мы раскладываем на множители, используя формулу разности кубов:

Задание. Основаниями усеченной пирамиды являются квадраты со сторонами 9 см и 5 см, а высота пирамиды составляет 6 см. Найдите ее объем.

Сначала вычислим площади оснований:

Объем конуса

Рассмотрим конус с высотой h и радиусом основания R. Совместим начало координат с вершиной конуса и направим ось Ох в сторону основания конуса. Тогда она пересечет основание в какой-то точке М c координатой h. Далее через точку М₁ на оси Ох, имеющей координату х, проведем сечение, перпендикулярное оси Ох. Это сечение будет окружностью.

Также построим образующую ОА, которая будет проходить через сечение в точке А₁. Теперь сравним ∆ОАМ и ∆ОА₁М₁. Они прямоугольные, и у них есть общий угол ∠АОМ. Это значит, что они подобны, и поэтому справедливо отношение:

Полученную формулу можно переписать в другом виде так, чтобы она содержала площадь основания, причем она будет похожа на аналогичную формулу для пирамиды:

Задание. Радиус конуса – 8 см, а его высота составляет 12 см. Определите его объем.

Решение. Здесь надо просто применить выведенную формулу:

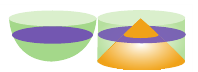
Задание. В сосуде, имеющем форму перевернутого конуса, вода доходит до уровня, соответствующего 2/3 высоты сосуда. При этом ее объем составляет 192 мл. Каков объем всего сосуда?

Решение. В задаче фигурируют два конуса. Один из них – это сам сосуд, а второй – его часть, заполненная водой. При выведении формулы объема мы уже выяснили, что радиусы таких конусов пропорциональны их высотам:

Мы уже заметили, что формулы для объема пирамида и конуса идентичны. По сути, конус можно рассматривать как особый случай пирамиды, у которой в основании лежит не многоугольник, а окружность. Аналогично и усеченный конус можно считать особым случаем усеченной пирамиды, а поэтому для расчета его объема можно применять такую же формулу:

Задание. Вычислите объем усеченного конуса с высотой 9 и радиусами оснований 7 и 4.

Решение. Сначала находим площади оснований:

Объем шара

Пришло время разобраться и с таким телом, как шар. Здесь можно использовать тот же метод интегрирования, что и в случае с конусом и пирамидой. Но можно поступить и иначе – использовать выведенную нами для тел вращения формулу

Шар как раз является телом вращения. Он получается при вращении полуокружности вокруг диаметра, на который эта дуга опирается.

Напомним известное нам уравнение окружности, чей центр совпадает с началом координат:

Здесь надо уточнить, что если у получившейся функции впереди записан знак «+», то ее график соответствует полуокружности, находящейся над осью Ох. Если же используется знак «–», то получается уже нижняя полуокружность, расположенная под осью Ох:

В принципе мы можем поворачивать любую из этих полуокружностей вокруг Ох, но мы выберем верхнюю полуокружность. Заметим, что эта дуга начинается в точке х = – R и заканчивается в точке х = R, эти числа будут пределами интегрирования. Тогда объем шара равен:

Задание. Найдите объем шара с радиусом 6.

Решение. Подставляем радиус из условия в формулу:

Задание. В цилиндр вписан шар. Во сколько раз объем цилиндра больше объема такого шара?

Решение. Ясно, что так как шар вписан в цилиндр, то радиусы этих тел одинаковы. Обозначим этот радиус как R. Также ясно, что раз шар касается оснований цилиндра, то расстояние между ними (то есть высота цилиндра) равно двум радиусам шара:

Шаровой сегмент

Когда плоскость проходит через шар, она рассекает его на две фигуры, которые именуются шаровым сегментом. Если из центра шара О провести радиус ОА длиной R в направлении плоскости сечения, который перпендикулярен этой плоскости, то он пересечет ее какой-то точке В. Длину отрезка АВ называют высотой шарового сегмента и обозначают буквой h:

Ясно, что при этом отрезок ОВ – это расстояние от секущей плоскости (или от основания сегмента) до центра шара, причем этот отрезок имеет длину R –h.

Можно считать, что шаровой сегмент, как и шар, получается при вращении дуги окружности вокруг оси Ох. Однако если сам шар при этом ограничен плоскостями x = R и х = – R, то сегмент ограничен другими плоскостями: х = R и х = R – h. Это значит, что его объем можно вычислить с помощью интеграла также, как и объем шара, отличаться будет лишь нижний предел интегрирования:

Заметим, что шар можно рассматривать как шаровой сегмент, чья высота вдвое больше его радиуса. И действительно, если в выведенную формулу мы подставим значение h = 2R, то получим уже известную нам формулу объема шара.

Задание. Найдите объем шарового сегмента высотой 6, если он отсечен от шара радиусом 15.

Решение. Используем выведенную формулу:

Задание. Диаметр шара разделили на три равных отрезка. Через концы этих отрезков провели секущие плоскости, перпендикулярные диаметру. Чему равен объем тела, заключенного между этими двумя плоскостями (оно называется шаровым слоем), если радиус шара обозначен буквой R?

Решение. Ясно, что для вычисления объема шарового слоя достаточно вычесть из объема шара объемы двух шаровых сегментов, образующихся при проведении секущих плоскостей. Так как они разделили диаметр на три одинаковых отрезка, то высота этих сегментов будет в три раза меньше диаметра шара:

Площадь сферы

В предыдущих уроках мы уже узнали формулу для вычисления площади сферы, однако тогда мы ее не доказывали. Однако теперь мы можем ее доказать, используя формулу объема шара. Но сначала напомним саму формулу:

Впишем сферу в многогранник с n гранями. Ясно, что расстояние от граней этого многогранника до центра сферы равно радиусы сферы R. Далее построим пирамиды, чьи вершины находятся в центре сферы, а основания – это грани многогранника. Заметим, что такие пирамиды будут иметь одинаковые высоты длиной R.

Обозначим площади граней многогранника как S₁, S₂, S₃,…S_n. Тогда объемы пирамид, построенных на этих гранях, вычисляются так:

Заметим, что в сумме эти объемы дают объем всего многогранника, а сумма площадей S₁, S₂, S₃,…S_n – это площадь всей его поверхности. Тогда можно записать:

Теперь начнем неограниченно уменьшать размеры граней многогранника. Тогда число n будет расти, объем многогранника будет приближаться к объему шара, а площадь многогранника – к площади к сфере. Тогда и доказанное равенство можно будет записать так:

Задание. Необходимо изготовить закрытый сосуд с заранее заданным объемом V. Предлагается два варианта формы этого сосуда – шар и куб. Так как поверхность сосуда покрывается очень дорогой краской, то необходимо выбрать вариант с меньшей площадью поверхности. Какую форму для сосуда следует выбрать?

Решение. Обозначим радиус шара как R, а ребро куба как а. Тогда можно записать:

Теперь надо выяснить, какое из полученных значений больше. Для этого поделим площадь куба на площадь сферы. Если получится число, большее единицы, то площадь куба больше:

Получившееся число больше единицы, ведь 6 больше числа π, равного 3,1415926… Значит, и площадь куба больше, а потому необходимо выбрать сосуд, имеющий форму шара.

Ответ: шар.

Примечание. Более сложными математическими методами можно доказать, что если второй сосуд имеет не форму куба, а вообще любую форму, отличную от шара, то всё равно следует выбирать именно сосуд в форме шара. То есть из всех поверхностей, ограничивающих определенный объем, именно сфера имеет наименьшую площадь. Этот факт имеет и физическое следствие – капли дождя и мыльные пузыри стремятся принять форму шара, также как и любые жидкости, находящиеся в невесомости.

Итак, мы научились вычислять объемы таких тел, как конус, пирамида, шар, призма. Также помощью интегрирования можно находить объемы и ещё более сложных тел, если мы можем составить функцию, описывающую площадь их сечения.

Тела и поверхности вращения. Шар. Цилиндр. Конус

Тела и поверхности вращения.

Шар. Цилиндр. Конус. Площади поверхности и объемы этих фигур.

Подробная теория с наглядными иллюстрациями и основные формулы.

Читай эту статью, здесь все это есть.

Всего за 15 минут ты полностью во всём разберешься!

Тело вращения – это тело в пространстве, которое возникает при вращении какой-нибудь плоской фигуры вокруг какой-нибудь оси.

Вот самый простой пример: цилиндр.

Берем прямоугольник и начинаем вращать его вокруг одной из сторон.

Смотри.

Было–вращаем–стало:

А теперь гораздо хитрее. Бывает так, что ось вращения находится далеко от фигуры, которая вращается.

Например, так:

Вращаем:

Что получится? Бублик. А по-научному – ТОР.

Ну и так вот можно любую фигуру вертеть вокруг любой оси, и будут получаться разные более или менее сложные тела вращения.

Ну, а поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.

Здесь мы рассмотрим подробно несколько тел вращения. Те, которые встречаются в школьных задачах. Это шар, цилиндр и конус.

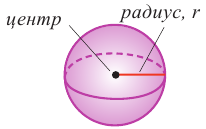
Шар

Шар – тело вращения, полученное вращением полуокружности вокруг диаметра.

Было–вращаем–стало:

Вообще-то есть и другое определение шара – через ГМТ (геометрическое место точек)

Шар – геометрическое место точек, удаленных от одной фиксированной точки на расстояние, не более заданного.

Скажу тебе по секрету, что, хоть второе определение и пугающее на вид, оно удобнее в обращении. Задумайся, ведь если тебя попросят сказать, что такое шар, ты скажешь что-то вроде:

«ну …там есть центр и радиус…», подразумевая, что все точки внутри шара находятся я на расстоянии не большем, чем радиус.

Ну, в общем, шар он и есть шар.

Названия, которые ты должен знать:

Незнакомое тебе, наверное, только одно.

Диаметральное сечение шара – сечение, проходящее через центр. Это сечение иногда еще называют большим кругом.

А вообще:

• Любое сечение шара – круг.
• Граница шара называется сфера. (Так же, как граница круга – окружность.)

Площадь поверхности сферы

( {{S}_{поверхности }}=4pi {{R}^{2}})

( R) – радиус

Откуда взялось? Умные математики придумали – это не так уж просто – придется просто запомнить.

Объем шара

( {{V}_{шара}}=frac{4}{3}pi {{R}^{3}})

( R) – радиус

Это еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.

Если ты знаком с производной, то можешь заметить это:

( {{V’}_{шара}}={{S}_{поверхности}})

И это не случайно! Но почему это так вышло, мы тоже здесь обсуждать не будем. Можешь попробовать доказать это сам!

Цилиндр

Цилиндр – тело, образованное вращением прямоугольника вокруг одной из сторон.

Вообще-то, полное имя этого тела – «прямой круговой цилиндр», но составители задач и мы вместе с ними по дружбе называем его просто цилиндром. Названия, относящиеся к цилиндру, такие:

Основания у цилиндра – это круги

Еще у цилиндра есть так называемая развертка.

Представь, что у нас от цилиндра осталась только боковая поверхность, и мы ее разрезали вдоль образующей и развернули.

Что получится? Представь себе, прямоугольник.

Развертка цилиндра – прямоугольник.

Площадь боковой поверхности цилиндра

( {{S}_{бок.}}=2pi RH)

( R) – радиус

( H) – высота, она же образующая.

Откуда взялась эта формула? Это как раз легко! Именно потому, что цилиндр можно развернуть, и получится прямоугольник ( 2pi Rcdot H).

Площадь этого прямоугольника и есть площадь боковой поверхности цилиндра. 

Площадь прямоугольника, как мы хорошо помним равна произведению сторон, поэтому

( {{S}_{бок.}}=2pi RH)

Площадь полной поверхности цилиндра

Прибавляем теперь площадь двух кругов – оснований и получаем:

( {{S}_{полн .}}=2pi RH+2pi {{R}^{2}})

Можно вынести (хотя и не обязательно) ( 2pi R):

( {{S}_{полн .}}=2pi Rleft( H+R right))

Но эту формулу неудобно запоминать!

Гораздо проще запомнить, что полная поверхность – сумма боковой поверхности и еще двух кругов – оснований, а боковая поверхность – прямоугольник. И тогда ( {{S}_{полн .}}) можно вообще не запоминать, ты всегда сам напишешь, что

( {{S}_{полн .}}=underbrace{2pi RH}_{прямоугольник}+underbrace{2pi {{R}^{2}}}_{два круга})

Объем цилиндра

( V=pi {{R}^{2}}H)

( R) – радиус основания ( H) – высота

Это точно как у призмы и параллелепипеда!

( V={{S}_{основания}}cdot H), только у призмы и параллелепипеда ( {{S}_{основания}}) — это площадь многоугольника, а у цилиндра ( {{S}_{основания}}) — это площадь круга.

Конус

Конус – тело вращения, образованное вращением прямоугольного треугольника вокруг одного из катетов.

Было–вращаем–стало:

И опять же, полное название этого тела: «прямой круговой конус», но во всех задачах у нас говорится просто «конус».

Названия, относящиеся к конусу:

Что тут нужно твердо помнить?

• Основание корпуса – круг
• Все образующие конуса – равны.

Ясно ли это? Вроде должно быть ясно, ведь образующая – это гипотенуза (одна и та же!) Треугольника, который вращаем, а радиус основания – катет.

У конуса тоже есть развертка.

Снова представим, что основания нет, разрежем боковую поверхность вдоль образующей и развернём кулек. Что получится?

Представь себе сектор круга. Пусть длина образующей равна ( l).

Развертка конуса – сектор круга радиуса ( l)

Площадь поверхности конуса

Как найти площадь боковой поверхности корпуса? Вспомним о развертке, ведь для цилиндра все было просто именно с помощью развертки.

По формуле площади сектора ( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}) Где ( alpha ) – угол при вершине в радианах.

И это уже формула. В некоторых задачах бывает дан именно угол при вершине в развертке конуса.

Но если все же даны только образующая и радиус основания, как быть?

Нужно осознать, что же такое дуга в развертке? Это бывшая окружность основания! Поэтому длина этой дуги равна ( 2pi R).

С другой стороны, длина этой же дуги равна ( alpha cdot l), так как это дуга окружности радиуса ( l). Поэтому

( alpha cdot l=2pi R)

Подставляем

( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}=frac{l}{2}cdot alpha cdot l=frac{l}{2}cdot 2pi R)

Итак,

( {{S}_{бок.}}=pi Rl), где

( R) — радиус окружности основания,

( l) — длина образующей

Ну, и осталось площадь полной поверхности конуса. Прибавим к боковой поверхности площадь круга основания, и получаем:

( {{S}_{полн. }}=pi Rl+pi {{R}^{2}})

Можно вынести ( pi R):

( {{S}_{полн. }}=pi Rleft( l+R right))

Но, как и для цилиндра, не надо запоминать вторую формулу, гораздо проще всегда пользоваться первой.

Объём конуса

( V=frac{1}{3}pi {{R}^{2}}H)

( R) – радиус основания (

H) – высота

Это так же, как у пирамиды

( V=frac{1}{3}{{S}_{осн.}}cdot H), только

( {{S}_{осн. }}) — это не площадь многоугольника, а площадь круга.

А вот откуда взялась ( frac{1}{3})?, по-прежнему остается загадкой, потому что эта ( frac{1}{3}) получена в результате довольно хитрых рассуждений умных математиков.

А тебе нужно очень твердо запомнить, что в формулах объёма «треугольных» фигур: конуса и пирамиды эта ( frac{1}{3}) и есть, а в формулах параллелепипеда, призмы и цилиндра ее нет!

Бонус: Вебинары по стереометрии из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 14 Стереометрия. Расстояние между точками и от точки до прямой

В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).

Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.

На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.

Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.

ЕГЭ 14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020

В этом видео:

• Как нарисовать шестиугольную пирамиду.
• Как подписать вершины пирамиды чтобы потом легче было решать задачу.
• Как исправить рисунок, если грани пирамиды сливаются.
• Доказательство пунктов А и Б, а также их правильная запись, которую примет любой проверяющий на ЕГЭ.
• Нахождение площади основания и объема пирамиды.
• Самое главное, на что нужно обратить внимание.

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

• тысячи учеников, поступивших в лучшие ВУЗы страны
• автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж — c 2003 года;
• в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
• отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Содержание:

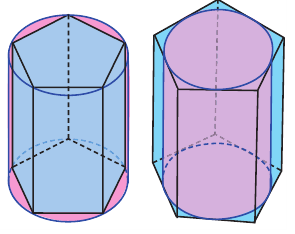
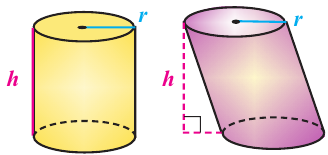
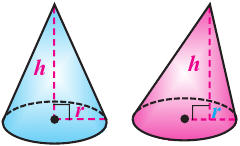
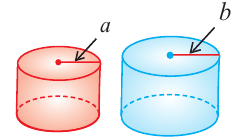
Говоря об объеме, имеют ввиду вместимость пространственной фигуры. Как вы думаете, емкость какого из цилиндров на рисунке больше?

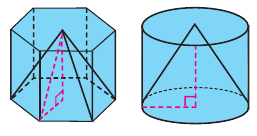
Призмой, вписанной (описанной) в цилиндр, называется призма, основания которой вписаны (описаны) в основания цилиндра.

Объем цилиндра

Пусть в цилиндр с радиусом

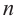
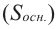
При бесконечном возрастании площадь оснований данных призм приближаются к площади основания цилиндра, а их объемы к объему цилиндра:

Объем цилиндра равен произведению площади основания на высоту.

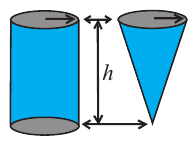
Практическая работа. Какая связь существует между объемами призмы и пирамиды, если они имеют одинаковые высоты и основания? Можно ли эту связь применить для объемов цилиндра и конуса?

Сделайте из картона модели сосудов в виде конуса и цилиндра, радиусы оснований и высоты которых одинаковы. Заполните цилиндрический сосуд при помощи сосуда в виде конуса (песком, рисом, и т. п.).

Сколько таких сосудов понадобится, чтобы заполнить цилиндрический сосуд? Верно ли утверждение, что цилиндрический сосуд можно заполнить тремя полными сосудами в виде конуса?

Обобщите соответствующую информацию о вычислении объема призмы, цилиндра, пирамиды и конуса, записав ответ в закрашенные ячейки.

Объем призмы и цилиндра:

Объем = площадь основания

Объем пирамиды и конуса:

Объем = объем призмы или цилиндра, имеющих одинаковые

основание и высоту.

Объем конуса

Объем конуса равен произведению одной третьей площади основания на высоту.

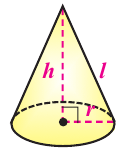
Пример №1

Образующая конуса 9 см, высота 6 см. Найдите объем конуса.

Решение:

Объем шара и его частей

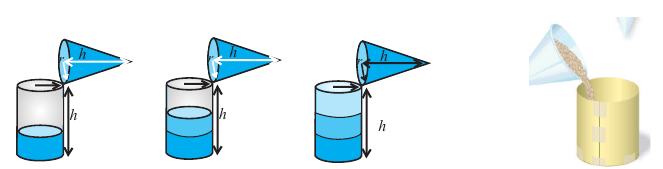
Практическая работа.

1. Возьмите мяч. Определите его диаметр.

2. Изобразите на бумаге развертку цилиндра, диаметр и высота которого равны диаметру шару.

3. Вырежьте и сверните полученную развертку в цилиндр без верхней крышки. Скрепите развертку при помощи клейкой ленты. Разделите высоту цилиндра на 3 равные части и сделайте соответствующие разметки.

4. Обверните мяч фольгой или плотным материалом и сделайте мешок сферической формы. Наполните его песком.

5. Пересыпьте песок в цилиндр. Какая часть цилиндра заполнится?

Если разделить поверхность шара сеткой из вертикальных и горизонтальных линий и маленький “прямоугольный” кусочек сферы соединить с центром шара, то можно представить, что шар состоит из множества “маленьких пирамид”.

Объем шара можно выразить через сумму объемов “маленьких пирамид” 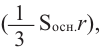высота которых равна радиусу шара. Бесконечно уменьшая размеры оснований, количество пирамид будет бесконечно расти.

Сумма площадей оснований “маленьких пирамид” будет равна площади поверхности шара. Учитывая, что площадь поверхности шара равна 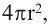получим формулу для нахождения объема шара:

Объем шара:

Объем шара равен произведению 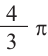и куба радиуса.

Пример №2

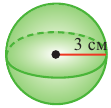
Найдите: а) объем шара радиуса 3 см

b) радиус шара объемом 288

Решение:

а)

b)

Сектор шара и сегмент шара

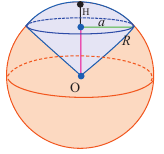
Шаровой сектор — это часть шара, ограниченная конической поверхностью с вершиной в центре шара. Шаровой сектор-объеденение конуса и шарового сегмента.

Так как шаровой сектор можно рассмотреть как предел суммы объемов маленьких пирамид, вершины которых находятся в центре шара, а основания касаются его поверхности, то

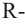
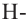
Здесь радиус шара, высота соответствующего сегмента

С другой стороны,

Проектная работа.

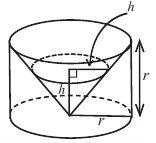
Отношение между объемами цилиндра, конуса и шара, которое получил Архимед.

Архимед нашел формулу для нахождения объема шара, исследовав связь между объемом цилиндра, описанного вокруг шара радиуса и объемом конуса, вписанного в данный цилиндр. Попробуйте и вы выполнить это исследование.

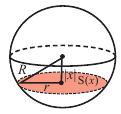
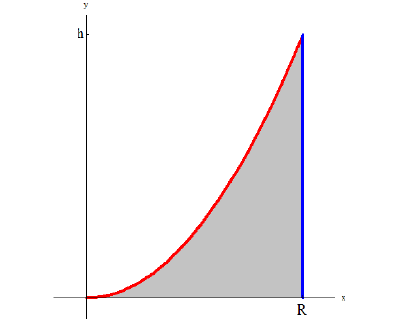
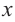
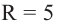
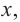
Если – расстояние от центра шара до плоскости сечения, то для шара радиуса представьте зависимость площади сечения от выполнив следующие шаги.

a) Вычислите следующие значения функции

Для примера найдено значение

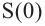
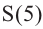
b) Представьте свои суждения о значениях и сечений.

c) Запишите общую формулу для определения площади сечения, расположенного на расстоянии 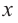от центра шара радиуса

d) Свяжите формулу, полученную в пункте 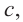и следующий рисунок.

e) Чтобы понять умозаключения Архимеда, вернемся к начальному рисунку.

При “извлечении” конуса из цилиндра в поперечном сечении получаем кольца, параллельные основанию.

На одном и том же уровне поперечное сечение шара является кругом. Из подобия треугольников можно доказать, что площадь кольца каждого слоя равна 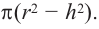Поскольку площади этих плоских сечений равны, по принципу Кавальери равны и объемы этих тел.

Объемы подобных фигур

Отношения соответствующих линейных размеров подобных пространствнных фигур должны быть равны.

По заданным соответствующим размерам подобных пространственных фигур можно найти неизвестные размеры.

Пример №3

Конусы 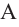и подобны. По данным рисунка найдите образующую конуса

Решение: Запишем отношение линейных размеров: Радиус А Образующая А

Известно, что отношение площадей поверхностей двух подобных пространственных фигур равно квадрату отношения соответствующих линейных размеров или квадрату коэффициента подобия:

Объемы подобных пространственных фигур

Отношение объемов подобных пространственных фигур 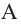и равно кубу отношения соответствующих линейных размеров или кубу коэффициента подобия:

Пример №4

Отношение боковых поверхностей двух подобных цилиндров равно 4:9. Зная, что разность объемов равна 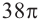куб.ед., найдите объемы цилиндров.

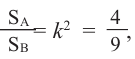
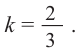
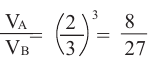
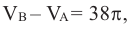
Решение: по условию тогда Значит С другой стороны, принимая во внимание, что получим:

Объемы тел в высшей математике

Под телом Т будем подразумевать ограниченное множество в пространстве.
Будем рассматривать тела, имеющие внутренние точки и границу, которая также принадлежит телу (замкнутые тела), причем такие, что любые две внутренние
точки можно соединить непрерывной линией, проходящей внутри тела.
 

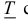
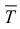
Определение 1. Рассмотрим тело составленное из конечного числа многогранников, содержащихся в Т, и тело , составленное из многогранников и покрывающее тело Т:
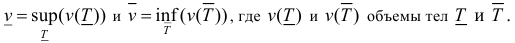
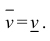
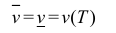
Пусть Тело называется кубируемым, если . При этом число (1) называется объемом тела Т (по Жордану).
 

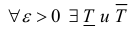
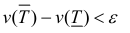
Замечание. Для кубируемости тела Т необходимо и достаточно, чтобы  такие, что  (2)

Пусть для кубируемого тела Т известны площади s=s(x) его сечения плоскостями перпендикулярными оси Ох, проходящими через точки (х, 0, 0),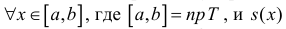 – непрерывна

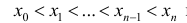
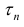
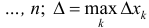
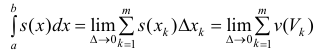
Разобьем отрезок [ a b ] на n частичных отрезков точками и обозначим это разбиение . Пусть 
 – диаметр разбиения, тогда (3)
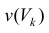
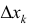
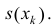
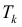
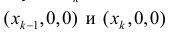
Где это – объем цилиндрического тела высотой  и площадью основания
 Пусть  k − -ый слой тела Т между плоскостями, проходящими через точки и перпендикулярными оси Ох.

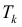
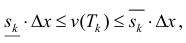
Так как Т – кубируемо, то  – также кубируемо и где

Тогда 
∀n ∈ N, или 

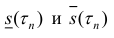
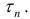
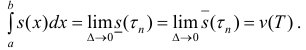
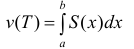
Гдеэто – нижняя и верхняя суммы Дарбу функции s(x) для разбиения
ПоэтомуТаким образом   (6)
 

Замечание. Нужно заметить, что неравенство (4), которое использовалось для вывода формулы (6), выполняется, когда любые два рассматриваемые сечения
тела Т при проекции на плоскость yOz полностью содержатся одно в другом.
Однако формула (6) верна и в общем случае. Для этого достаточно потребовать,
чтобы тело Т было кубируемым и функция s (x) – непрерывной.

Пример №5

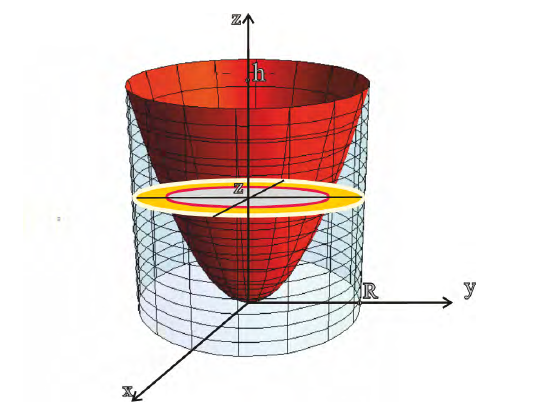
Найти объем тела ограниченного поверхностями 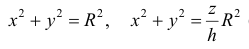 (ниже параболоида).
 

Решение.

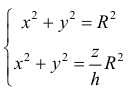
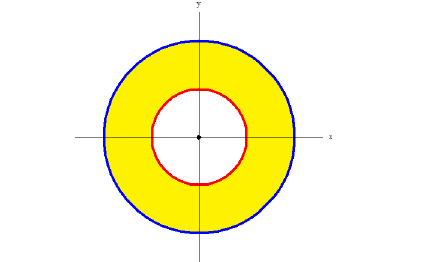
Из системы уравнений   следует, что z=h.

В сечении тела плоскостью проходящей через точку (0, 0, z) перпендикулярно оси Оz получается кольцо

Радиус внешней окружности равен R, радиус внутренней равен 
Поэтому по формуле (6):

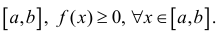
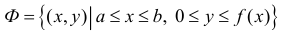
Формулу (6) удобно применять к телам вращения. Пусть y=f(x) – непрерывна на отрезке  Будем вращать криволинейную трапецию
 

вокруг оси Ох. Получим тело:

Тогда сечением полученного тела плоскостью проходящей через точку (х,0,0) и перпендикулярной оси Ох будет круг радиуса 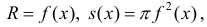 и по формуле (6): 
Где y=f(x).
Аналогично, если 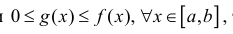то при вращении вокруг оси Ох фигуры

Получим тело, объем которого 
 

Пример №6

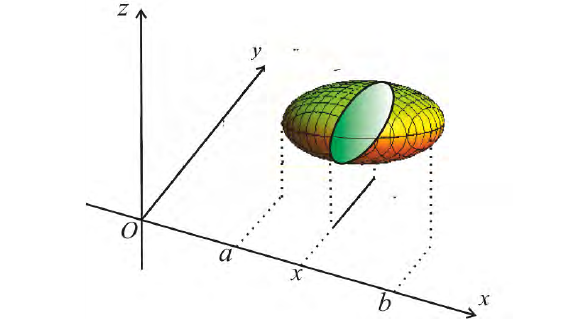
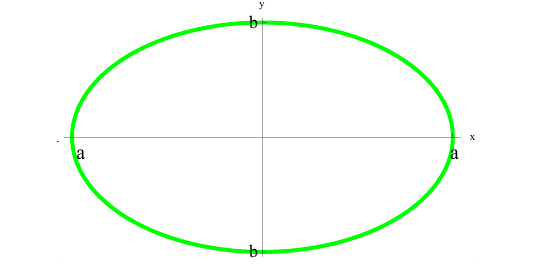
Рассмотрим фигуру Φ ограниченную эллипсом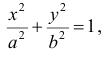  
Найдем объем эллипсоида полученного при вращении вокруг оси Ох фигуры Φ .
 

Решение.

По формуле (7): 
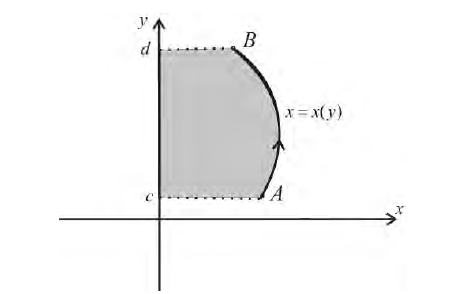
Пусть функция x=x(y) – непрерывна при 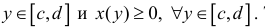Тогда, аналогично, при вращении вокруг оси Оу фигуры 

Получим тело, объем которого 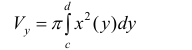(9)
Если же вращать вокруг оси Оу трапецию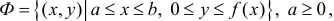  

то 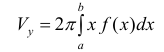(10)
 

Пример №7

Рассмотрим тело Т из примера 1. Оно получается, если вращать вокруг оси Oz фигуру, ограниченную линиями:

Из первого уравнения найдем 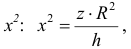поэтому по формуле (9):

 

Пример №8

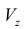
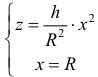
Пример №9

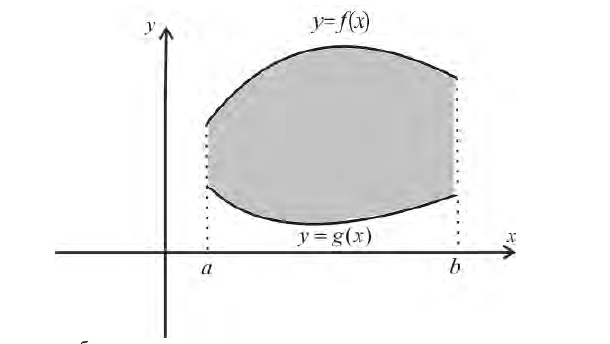
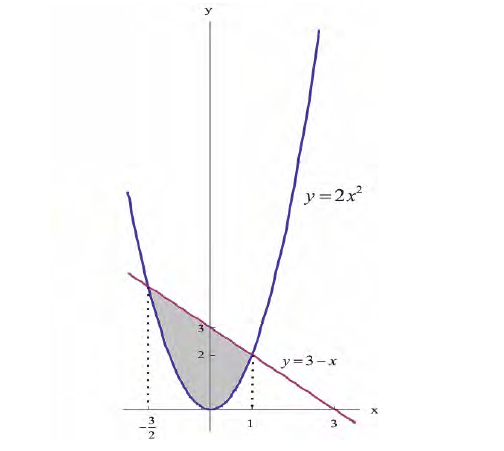
Фигура Ф ограничена линиями 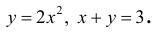 Найти
 

Решение.

Абсциссы точек пересечения: 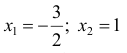 (см. пример 1 § 30). По формуле (8):

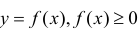
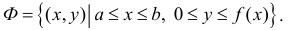
Замечание. Для непрерывной функции рассмотрим криволинейную трапецию  

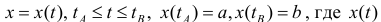
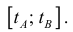
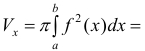
Пусть – непрерывно-дифференцируема на промежуткеТогда по формуле (7): по формуле (1) § 26

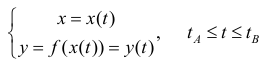
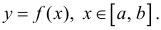
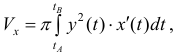
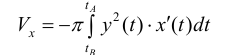
Где – параметрическое задание линии  Таким образом  или (12)
(кривая обходится так, чтобы область Ф оставалась слева).

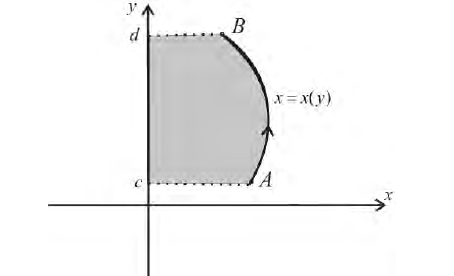
Аналогично, для непрерывной функции 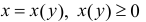рассмотрим криволинейную трапецию 

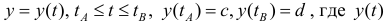
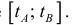
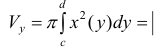
Пусть – непрерывно-дифференцируема на промежутке Тогда по формуле (9): по формуле (1) § 26

Где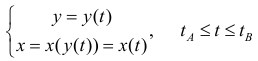 – параметрическое задание линии 

Таким образом 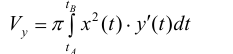(13)   (кривая обходится так, чтобы область Ф оставалась слева).

Рассмотрим область ,ограниченную простой замкнутой кривой
 (кривая лежит по одну сторону от оси Ox ). Тогда объем  можно находить по формуле (12): 
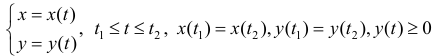
(кривая обходится так, чтобы область оставалась слева).

Аналогично ,для области ограниченной простой замкнутой кривой
 (кривая лежит по одну сторону от оси Oy )объем  можно находить по формуле (13): (кривая обходится так, чтобы область оставалась слева).

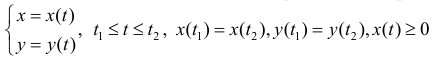
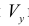
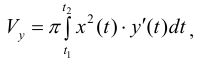
Пример №10

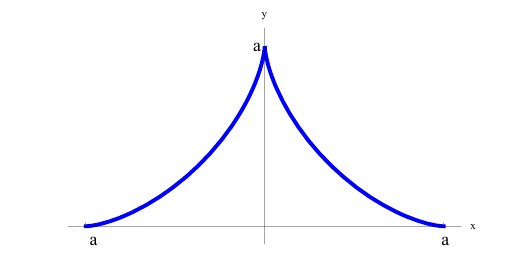
Дана астроида 

Найдем .
 

Решение.

по формуле (12):

 

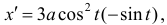
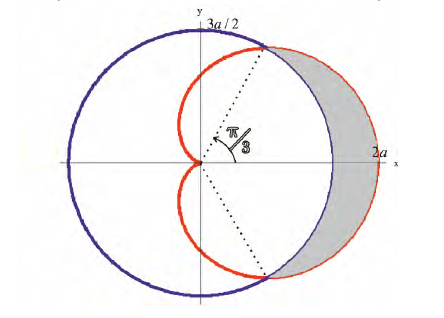
Пример №11

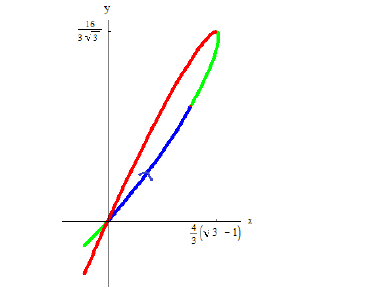
Петля кривой 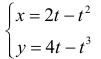вращается вокруг оси Ox .Найти .
 

Решение.

петля обходится против часовой стрелки. По формуле (12):

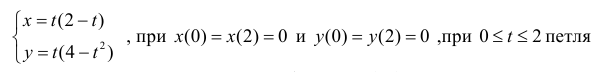
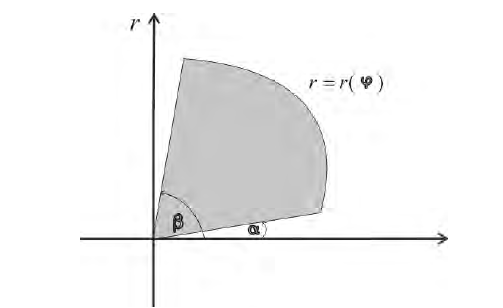
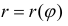
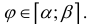
Пусть – кривая в полярной системе координат, r (ϕ) – непрерывна при  Рассмотрим на плоскости хОу криволинейный сектор

Тогда объем тела при вращении фигуры ϕ вокруг полярной оси равен
 (14)

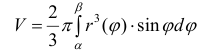
Пример №12

(см. пример 4 § 31).

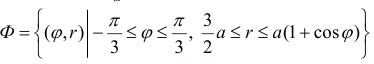
Найдем .
 

Решение.

По формуле (14):