Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 февраля 2020 года; проверки требуют 36 правок.
| Тессеракт | |
|---|---|

|
|
| Тип | Правильный четырёхмерный политоп |
| Символ Шлефли | {4,3,3} |
| Ячеек | 8 |
| Граней | 24 |
| Рёбер | 32 |
| Вершин | 16 |
| Вершинная фигура | Правильный тетраэдр |
| Двойственный политоп | 16-ячейник |

Анимированная проекция вращающегося тессеракта
Тессера́кт (от др.-греч. τέσσαρες ἀκτῖνες — «четыре луча») — четырёхмерный гиперкуб, аналог обычного трёхмерного куба в четырёхмерном пространстве. Другие названия: 4-куб, тетраку́б, восьмияче́йник[1], октахо́р (от др.-греч. οκτώ «восемь» + χώρος «место, пространство»), гиперкуб (если число измерений не оговаривается). Тессеракт — один из шести правильных многоячейников в четырёхмерном пространстве.
Согласно Оксфордскому словарю, слово «тессеракт» было придумано Чарльзом Говардом Хинтоном (1853—1907) и впервые использовано в 1888 году в его книге «Новая эра мысли».
Геометрия[править | править код]
Обычный тессеракт в евклидовом четырёхмерном пространстве определяется как выпуклая оболочка точек (±1, ±1, ±1, ±1). Иначе говоря, он может быть представлен в виде следующего множества:
Тессеракт ограничен восемью гиперплоскостями 
Четырёхмерный гиперобъём тессеракта со стороной длины a рассчитывается по формуле:

Объём же гиперповерхности тессеракта можно найти по формуле:

Радиус описанной гиперсферы:

Радиус вписанной гиперсферы:

Популярное описание[править | править код]
Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из трёхмерного пространства.
В одномерном «пространстве» — на линии — выделим отрезок АВ длиной L.
На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат CDBA. Повторив эту операцию с плоскостью, получим трёхмерный куб CDBAEGHF. А сдвинув куб в четвёртом измерении (перпендикулярно первым трём) на расстояние L, мы получим гиперкуб CDBAGHFEKLJIOPNM.
Построение тессеракта на плоскости

Развёртка тессеракта
Одномерный отрезок АВ служит стороной двумерного квадрата CDBA, квадрат — стороной куба CDBAEGHF, который, в свою очередь, будет стороной четырёхмерного гиперкуба. Отрезок прямой имеет две граничные точки, квадрат — четыре вершины, куб — восемь. В четырёхмерном гиперкубе, таким образом, окажется 16 вершин: 8 вершин исходного куба и 8 сдвинутого в четвёртом измерении. Он имеет 32 ребра — по 12 дают начальное и конечное положения исходного куба, и ещё 8 рёбер «нарисуют» восемь его вершин, переместившихся в четвёртое измерение. Те же рассуждения можно проделать и для граней гиперкуба. В двумерном пространстве она одна (сам квадрат), у куба их 6 (по две грани от переместившегося квадрата и ещё четыре опишут его стороны). Четырёхмерный гиперкуб имеет 24 квадратные грани — 12 квадратов исходного куба в двух положениях и 12 квадратов от двенадцати его рёбер.
Как сторонами квадрата являются 4 одномерных отрезка, а сторонами (гранями) куба являются 6 двухмерных квадратов, так и для «четырёхмерного куба» (тессеракта) сторонами являются 8 трёхмерных кубов. Пространства противоположных пар кубов тессеракта (то есть трёхмерные пространства, которым эти кубы принадлежат) параллельны. На рисунке это кубы: CDBAEGHF и KLJIMOPN, CDBAKLJI и GHFEOPNM, EFBAMNJI и GHDCOPLK, CKIAGOME и DLJBHPNF.
Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трёхмерного пространства, будет выглядеть четырёхмерный гиперкуб. Воспользуемся для этого уже знакомым методом аналогий.
Возьмём проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединённые четырьмя линиями — боковыми рёбрами. Аналогичным образом четырёхмерный гиперкуб в пространстве трёх измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединённых восемью рёбрами. При этом сами «ящики» — трёхмерные грани — будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в направлении четвёртой оси. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.
Подобно тому, как трёхмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвёртое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Сам же четырёхмерный гиперкуб состоит из бесконечного количества кубов, подобно тому как трёхмерный куб можно «нарезать» на бесконечное количество плоских квадратов.
Разрезав шесть граней трёхмерного куба, можно разложить его в плоскую фигуру — развёртку. Она будет иметь по квадрату с каждой стороны исходной грани плюс ещё один — грань, ей противоположную. А трёхмерная развёртка четырёхмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс ещё одного — конечной «гиперграни».
Свойства тессеракта представляют собой продолжение свойств геометрических фигур меньшей размерности в четырёхмерное пространство.
Развёртки тессеракта[править | править код]

Разворачивание поверхности тессеракта в трёхмерное пространство
Аналогично тому, как поверхность куба может быть развёрнута в многоугольник, состоящий из шести квадратов, поверхность тессеракта может быть развёрнута в трёхмерное тело, состоящее из восьми кубов[2].
Существует 261 развёртка тессеракта[3].
Развёртки гиперкуба могут быть найдены перечислением «сдвоенных деревьев», где «сдвоенное дерево» (paired tree) — это дерево с чётным числом вершин, которые разбиты на пары так, что ни одна пара не состоит из двух смежных вершин. Между «сдвоенными деревьями» с 8 вершинами и развёртками тессеракта существует взаимно однозначное соответствие. Всего существует 23 дерева с 8 вершинами, при разбиении вершин которых на пары несмежных вершин получается 261 «сдвоенное дерево» с 8 вершинами[4].
Крестообразная развёртка тессеракта является элементом картины Сальвадора Дали «Corpus Hypercubus» (1954)[5].
В рассказе Роберта Хайнлайна «Дом, который построил Тил» калифорнийский архитектор Квинтус Тил строит дом в форме развёртки гиперкуба, который во время землетрясения складывается в тессеракт[5].
Проекции[править | править код]
На двумерное пространство[править | править код]
Данная структура сложна для воображения, но возможно спроецировать тессеракт в двумерные или трёхмерные пространства. Кроме того, проецирование на плоскость позволяет легко понять расположение вершин гиперкуба. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения в пределах тессеракта, но которые иллюстрируют структуру связи вершин, как в предыдущих примерах:
|
Первая картинка показывает, как тессеракт получен в результате комбинирования двух кубов. Схема подобна построению куба от двух квадратов |
Вторая картинка иллюстрирует тот факт, что все рёбра тессеракта имеют одинаковую длину. Она примечательна тем, что все восемь кубов имеют одинаковый вид. |
Третья картинка демонстрирует тессеракт в изометрии, относительно точки построения. Это изображение представляет интерес при использовании тессеракта как основания для топологической сети, чтобы связать многократные процессоры в параллельных вычислениях. |
На трёхмерное пространство[править | править код]

Вращающаяся модель тессеракта. Эта модель показывает грани тессеракта — равные кубы
Одна из проекций тессеракта на трёхмерное пространство представляет собой два вложенных трёхмерных куба, соответствующие вершины которых соединены между собой отрезками.
Внутренний и внешний кубы имеют разные размеры в трёхмерном пространстве, но в четырёхмерном пространстве это равные кубы. Для понимания равности всех кубов тессеракта была создана вращающаяся модель тессеракта.
- Шесть усечённых пирамид по краям тессеракта — это изображения равных шести кубов. Однако эти кубы для тессеракта — как квадраты (грани) для куба. Но на самом деле тессеракт можно разделить на бесконечное количество кубов, как куб — на бесконечное количество квадратов, или квадрат — на бесконечное число отрезков.
Ещё одна интересная проекция тессеракта на трёхмерное пространство представляет собой ромбододекаэдр с проведёнными четырьмя его диагоналями, соединяющими пары противоположных вершин при больших углах ромбов. При этом 14 из 16 вершин тессеракта проецируются в 14 вершин ромбододекаэдра, а проекции 2 оставшихся совпадают в его центре. В такой проекции на трёхмерное пространство сохраняются равенство и параллельность всех одномерных, двухмерных и трёхмерных сторон.
Стереопара[править | править код]
Стереопара тессеракта изображается как две проекции на плоскость одного из вариантов трёхмерного представления тессеракта. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопический эффект, позволяющий лучше воспринять проекцию тессеракта на трёхмерное пространство.

Тессеракт в культуре[править | править код]
- В рассказе «Дом, который построил Тил» (англ. And He Built a Crooked House; «И построил он себе скрюченный домишко») Хайнлайна описан восьмикомнатный дом в форме развёрнутого тессеракта.
- Рассказ Генри Каттнера «Все тенали бороговы» (англ. Mimsy Were the Borogoves) описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.
- В рассказе Роберта Шекли «Мисс Мышка и четвёртое измерение» писатель-эзотерик, знакомец автора, пытается увидеть тессеракт, часами глядя на сконструированный им прибор: шар на ножке с воткнутыми в него стержнями, на которые насажены кубы, обклеенные всеми подряд эзотерическими символами. В рассказе упоминается труд Хинтона.
- В фантастическом рассказе Марка Клифтона «На ленте Мёбиуса» дети-вундеркинды путешествуют через пространство и время, используя модели ленты Мёбиуса, бутылки Клейна и тессеракта.
- В Кинематографической вселенной Marvel Тессеракт является артефактом-носителем одного из шести Камней Бесконечности.
- Сюжет фильма Анджея Секулы «Куб 2: Гиперкуб» разворачивается внутри лабиринта из комнат, помещённого в гиперкуб.
- В научно-фантастическом фильме «Интерстеллар» главный герой Джозеф Купер и робот ТАРС после пересечения горизонта событий Гаргантюа – сверхмассивной чёрной дыры – оказываются внутри массивного тессеракта, построенного людьми будущего.
- В музыке группа в стиле металл (Tesseract), отличающаяся сложными, сменяющимися ритмами, джентом (djent).
Примечания[править | править код]
- ↑ Д. К. Бобылёв. Четырехмерное пространство // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ Gardner, 1989, pp. 48—50.
- ↑ Gardner, 1989, p. 272: «Peter Turney, in his 1984 paper „Unfolding the Tesseract“, uses graph theory to show that there are 261 distinct unfoldings.».
- ↑ Peter Turney. Unfolding the Tesseract (англ.) // Journal of Recreational Mathematics : journal. — 1984-85. — Vol. 17, no. 1. Архивировано 25 июля 2018 года.
- ↑ 1 2 Gardner, 1989, p. 50.
Литература[править | править код]
- Charles H. Hinton. Fourth Dimension, 1904. ISBN 0-405-07953-2
- Gardner M. Mathematical Carnival. — Washington, D.C.: MAA, 1989. — P. 41—54, 272. — ISBN 0-88385-448-1.
- Ian Stewart, Concepts of Modern Mathematics, 1995. ISBN 0-486-28424-7
- Гальперин Г.А. Многомерный куб. — М.: МЦНМО, 2015. — 80 с. — ISBN 978-5-4439-0296-8.
- Дужин С., Рубцов В. Четырехмерный куб // Квант. — 1986. — № 6. — С. 3—7.
Ссылки[править | править код]
- На русском языке
- Получение из развертки
- Гиперкуб
- Программа Transformator4D. Формирование моделей трёхмерных проекций четырёхмерных объектов (в том числе и Гиперкуба).
- Программа, реализующая построение тессеракта и все его аффинные преобразования, с исходниками на C++.
- Стереопара тессеракта с ребрами одинаковой длины.
- Вращение тессеракта — проекция в трёхмерном пространстве
- На английском языке
- Tesseract
- Cut The Knot! The Tesseract
- Charles Howard Hinton
- A four dimensional version of Rubik’s Cube
- Fourth Dimension: Tetraspace
- Mushware Limited — программа вывода тессеракта (Tesseract Trainer, лицензия совместима с GPLv2) и шутер от первого лица в четырёхмерном пространстве (Adanaxis; графика, в основном, трёхмерная; есть версия под GPL в репозиториях ОС).
| Основные выпуклые правильные и однородные политопы в размерностях 2—10 | |||||
|---|---|---|---|---|---|
| Семейство | An | Bn | I₂(p) / Dn | E₆ / E₇ / E₈ / F₄ / G₂ | H₄ |
| Правильный многоугольник | Правильный треугольник | Квадрат | Правильный p-угольник |
Правильный шестиугольник | Правильный пятиугольник |
| Однородный многогранник | Правильный тетраэдр | Правильный октаэдр • Куб | Полукуб | Правильный додекаэдр • Правильный икосаэдр | |
| Однородный многоячейник | Пятиячейник | 16-ячейник • Тессеракт | Полутессеракт | 24-ячейник | 120-ячейник • 600-ячейник |
| Однородный 5-политоп | Правильный 5-симплекс | 5-ортоплекс • 5-гиперкуб | 5-полугиперкуб | ||
| Однородный 6-политоп | Правильный 6-симплекс | 6-ортоплекс • 6-гиперкуб | 6-полугиперкуб | 122 • 221 | |
| Однородный 7-политоп | Правильный 7-симплекс | 7-ортоплекс • 7-гиперкуб | 7-полугиперкуб | 132 • 231 • 321 | |
| Однородный 8-политоп | Правильный 8-симплекс | 8-ортоплекс • 8-гиперкуб | 8-полугиперкуб | 142 • 241 • 421 | |
| Однородный 9-политоп | Правильный 9-симплекс | 9-ортоплекс • 9-гиперкуб | 9-полугиперкуб | ||
| Однородный 10-политоп | Правильный 10-симплекс | 10-ортоплекс • 10-гиперкуб | 10-полугиперкуб | ||
| Однородный n-политоп | Правильный n-симплекс | n-ортоплекс • n-гиперкуб | n-полугиперкуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник |
| Темы: Семейства политопов • Правильные политопы • Список правильных политопов и их соединений |
Подписывайтесь на канал в Яндекс. Дзен или на канал в телеграм “Математика не для всех”, чтобы не пропустить интересующие Вас материалы. Также есть группы в VK, Одноклассниках и Facebook : всё для математического просвещения!
В массовом сознании слово “тессеракт” укоренилось, как это не горько признавать, через голливудскую франшизу Мстители. Однако, настоящим основоположником этого понятия является Чарльз Говард Хинтон – британский математик, впервые употребивший его в книге “Эра новой мысли”.
Хотя первенство в теоретическом описании высших измерений принадлежит великому Бернхарду Раману, Чарльз Хинтон одним из первых стал описывать “физические” пространства с размерностью выше 3, Он, кстати, утверждал, что путем длительных фантазий и рассуждений, ему удалось полностью научиться визуализировать 4-мерные фигуры в своей голове. Представить 4-мерные фигуры возможно двумя способами: разверткой и проекцией. Рассмотрим оба.
Визуализация тессеракта
Для начала следует понимать, что привычное нам 3-х мерное пространство – это всего лишь частный случай n-мерного. Например, при n=0 мы получаем точку, при n=1 – одномерное пространство (например, множество точек, находящихся на прямой или отрезке), при n=2 – плоскость, квадрат.
Теперь возьмем квадрат ABCD и передвинем его точки в направлении, перпендикулярном существующим на рисунке. Получим 3-куб:
Теперь же по аналогии произведем параллельный перенос 3-куба. Важно понимать, что этот перенос тоже в перпендикулярном направлении, но на рисунке, это показать невозможно. Вот такой в итоге получается 4-куб или тессеракт:
У тессеракта 24 грани (квадраты от исходных кубов), 16 вершин и 32 ребра. Также как и для 3-куба для тессеракта существуют формулы вычисления объема, площади гиперповерхности, а также радиусов вписанных и описанных гиперсфер:
Еще одним способом визуализации тессеракта является развертка. Так как сторонами 4-куба являются восемь 3-кубов, его крестообразная развертка (всего разверток 261 штука) выглядит так:
Однако самым наглядным представлением тессеракта является “куб в кубе”:
Еще проще тессеракт выглядит на плоскости:
Где использовался тессеракт?
Больше всего упоминаний тессеракта в художественной литературе и кинематографе: от фантастических произведений Роберта Шекли до уже ставших культовыми “Мстителей”, серии фильмов “Куб” и “Интерстеллар”. Однако, мне кажется, что самой ярким использованием тессеракта является картина Сальвадора Дали “Распятие или гиперкубическое тело”
Гиф-анимации тессеракта
*************************************************************************
Путеводитель по каналу “Математика не для всех” – здесь собрано больше 100 статей на самые разнообразные темы: как для новичков, так и для более начитанных математиков! Например, почитайте про самые красивые математические формулы.
Второй проект – канал “Русский язык не для всех”
Спасибо! Надеюсь, было очень интересно и познавательно! Буду рад, если Вы поддержите меня ПОДПИСКОЙ, ЛАЙКОМ или даже критическим комментарием. ССЫЛКА НА ДЗЕН-КАНАЛ и TELEGRAM.
**************************************************************************
- Скачать PDF
- Детская площадка
- Здоровье
- Инженерное дело
- математика
- физика
- финансовый
- Химия
Гиперобъем Тессеракта Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 4D геометрия ↺ | |
| 4D геометрия | Тессеракт ↺ |
|
✖Длина края Тессеракта — это длина любого края четырехмерного объекта Тессеракт, который является четырехмерным расширением куба в трехмерном пространстве и квадрата в двумерном.ⓘ Длина края тессеракта [le] |
+10% -10% |
|
✖Гиперобъем Тессеракта — это 4-х мерный объем четырехмерного объекта Тессеракт, который является четырехмерным расширением куба в трехмерном пространстве и квадрата в двухмерном.ⓘ Гиперобъем Тессеракта [Hvolume] |
⎘ копия |
Формула
✖
Гиперобъем Тессеракта
Формула
`”H”_{“volume”} = “l”_{“e”}^4`
Пример
`”625m⁴”=(“5m”)^4`
Калькулятор
👍
Гиперобъем Тессеракта Решение
ШАГ 0: Сводка предварительного расчета
Используемая формула
Гиперобъем Тессеракта = Длина края тессеракта^4
Hvolume = le^4
В этой формуле используются 2 Переменные
Используемые переменные
Гиперобъем Тессеракта – (Измеряется в Метр⁴) – Гиперобъем Тессеракта — это 4-х мерный объем четырехмерного объекта Тессеракт, который является четырехмерным расширением куба в трехмерном пространстве и квадрата в двухмерном.
Длина края тессеракта – (Измеряется в метр) – Длина края Тессеракта — это длина любого края четырехмерного объекта Тессеракт, который является четырехмерным расширением куба в трехмерном пространстве и квадрата в двумерном.
ШАГ 1. Преобразование входов в базовый блок
Длина края тессеракта: 5 метр –> 5 метр Конверсия не требуется
ШАГ 2: Оцените формулу
Подстановка входных значений в формулу
Hvolume = le^4 –> 5^4
Оценка … …
Hvolume = 625
ШАГ 3: Преобразуйте результат в единицу вывода
625 Метр⁴ –> Конверсия не требуется
ОКОНЧАТЕЛЬНЫЙ ОТВЕТ
625 Метр⁴ <– Гиперобъем Тессеракта
(Расчет завершен через 00.004 секунд)
Кредиты

ИИТ Мадрас
(ИИТ Мадрас),
Ченнаи
Джасим К. создал этот калькулятор и еще 100+!

Институт дипломированных и финансовых аналитиков Национального колледжа Индии
(Национальный колледж ИКФАИ),
ХУБЛИ
Наяна Пульфагар проверил этот калькулятор и еще 900+!
3 Тессеракт Калькуляторы
Площадь поверхности Тессеракта
Идти
Площадь поверхности Тессеракта = 24*(Длина края тессеракта^2)
Поверхностный объем Тессеракта
Идти
Поверхностный объем Тессеракта = 8*(Длина края тессеракта^3)
Гиперобъем Тессеракта
Идти
Гиперобъем Тессеракта = Длина края тессеракта^4
Гиперобъем Тессеракта формула
Гиперобъем Тессеракта = Длина края тессеракта^4
Hvolume = le^4
-
English
Spanish
French
German
Italian
Portuguese
Polish
Dutch
Copied!
From Wikipedia, the free encyclopedia
| Tesseract 8-cell (4-cube) |
|
|---|---|
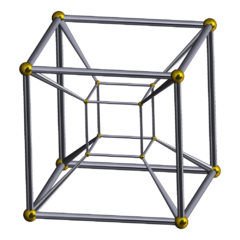
Schlegel diagram |
|
| Type | Convex regular 4-polytope |
| Schläfli symbol | {4,3,3} t0,3{4,3,2} or {4,3}×{ } t0,2{4,2,4} or {4}×{4} t0,2,3{4,2,2} or {4}×{ }×{ } t0,1,2,3{2,2,2} or { }×{ }×{ }×{ } |
| Coxeter diagram | |
| Cells | 8 {4,3} |
| Faces | 24 {4} |
| Edges | 32 |
| Vertices | 16 |
| Vertex figure |  Tetrahedron |
| Petrie polygon | octagon |
| Coxeter group | B4, [3,3,4] |
| Dual | 16-cell |
| Properties | convex, isogonal, isotoxal, isohedral, Hanner polytope |
| Uniform index | 10 |
![]()
Look up tesseract in Wiktionary, the free dictionary.


The tesseract can be unfolded into eight cubes into 3D space, just as the cube can be unfolded into six squares into 2D space.
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square.[1] Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes.
The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid,[2] cubic prism, and tetracube.[3] It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercubes or measure polytopes.[4] Coxeter labels it the 
The Oxford English Dictionary traces the word tesseract to Charles Howard Hinton’s 1888 book A New Era of Thought. The term derives from the Greek téssara (τέσσαρα ‘four’) and from aktís (ἀκτίς ‘ray’), referring to the four edges from each vertex to other vertices. Hinton originally spelled the word as tessaract.[6]
Geometry[edit]
As a regular polytope with three cubes folded together around every edge, it has Schläfli symbol {4,3,3} with hyperoctahedral symmetry of order 384. Constructed as a 4D hyperprism made of two parallel cubes, it can be named as a composite Schläfli symbol {4,3} × { }, with symmetry order 96. As a 4-4 duoprism, a Cartesian product of two squares, it can be named by a composite Schläfli symbol {4}×{4}, with symmetry order 64. As an orthotope it can be represented by composite Schläfli symbol { } × { } × { } × { } or { }4, with symmetry order 16.
Since each vertex of a tesseract is adjacent to four edges, the vertex figure of the tesseract is a regular tetrahedron. The dual polytope of the tesseract is the 16-cell with Schläfli symbol {3,3,4}, with which it can be combined to form the compound of tesseract and 16-cell.
Each edge of a regular tesseract is of the same length. This is of interest when using tesseracts as the basis for a network topology to link multiple processors in parallel computing: the distance between two nodes is at most 4 and there are many different paths to allow weight balancing.
Coordinates[edit]
The standard tesseract in Euclidean 4-space is given as the convex hull of the points (±1, ±1, ±1, ±1). That is, it consists of the points:
In this Cartesian frame of reference, the tesseract has radius 2 and is bounded by eight hyperplanes (xi = ±1). Each pair of non-parallel hyperplanes intersects to form 24 square faces in a tesseract. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex. All in all, it consists of 8 cubes, 24 squares, 32 edges, and 16 vertices.
Net[edit]
An unfolding of a polytope is called a net. There are 261 distinct nets of the tesseract.[7] The unfoldings of the tesseract can be counted by mapping the nets to paired trees (a tree together with a perfect matching in its complement).
Construction[edit]

The construction of hypercubes can be imagined the following way:
- 1-dimensional: Two points A and B can be connected to become a line, giving a new line segment AB.
- 2-dimensional: Two parallel line segments AB and CD separated by a distance of AB can be connected to become a square, with the corners marked as ABCD.
- 3-dimensional: Two parallel squares ABCD and EFGH separated by a distance of AB can be connected to become a cube, with the corners marked as ABCDEFGH.
- 4-dimensional: Two parallel cubes ABCDEFGH and IJKLMNOP separated by a distance of AB can be connected to become a tesseract, with the corners marked as ABCDEFGHIJKLMNOP. However, this parallel positioning of two cubes such that their 8 corresponding pairs of vertices are each separated by a distance of AB can only be achieved in a space of 4 or more dimensions.
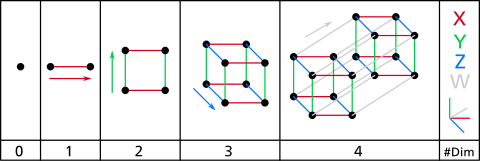
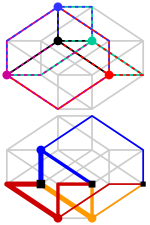
The 8 cells of the tesseract may be regarded (three different ways) as two interlocked rings of four cubes.[8]
The tesseract can be decomposed into smaller 4-polytopes. It is the convex hull of the compound of two demitesseracts (16-cells). It can also be triangulated into 4-dimensional simplices (irregular 5-cells) that share their vertices with the tesseract. It is known that there are 92487256 such triangulations[9] and that the fewest 4-dimensional simplices in any of them is 16.[10]
The dissection of the tesseract into instances of its characteristic simplex (a particular orthoscheme with Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() ) is the most basic direct construction of the tesseract possible. The characteristic 5-cell of the 4-cube is a fundamental region of the tesseract’s defining symmetry group, the group which generates the B4 polytopes. The tesseract’s characteristic simplex directly generates the tesseract through the actions of the group, by reflecting itself in its own bounding facets (its mirror walls).
) is the most basic direct construction of the tesseract possible. The characteristic 5-cell of the 4-cube is a fundamental region of the tesseract’s defining symmetry group, the group which generates the B4 polytopes. The tesseract’s characteristic simplex directly generates the tesseract through the actions of the group, by reflecting itself in its own bounding facets (its mirror walls).
Radial equilateral symmetry[edit]
The long radius (center to vertex) of the tesseract is equal to its edge length; thus its diagonal through the center (vertex to opposite vertex) is 2 edge lengths. Only a few uniform polytopes have this property, including the four-dimensional tesseract and 24-cell, the three-dimensional cuboctahedron, and the two-dimensional hexagon. In particular, the tesseract is the only hypercube (other than a 0-dimensional point) that is radially equilateral. The longest vertex-to-vertex diameter of an n-dimensional hypercube of unit edge length is √n, so for the square it is √2, for the cube it is √3, and only for the tesseract it is √4, exactly 2 edge lengths.
In unit-radius coordinates the unit-edge-length tesseract’s coordinates are:
- (±1/2, ±1/2, ±1/2, ±1/2)
Formulas[edit]
For a tesseract with side length s:
As a configuration[edit]
This configuration matrix represents the tesseract. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole tesseract. The nondiagonal numbers say how many of the column’s element occur in or at the row’s element.[11] For example, the 2 in the first column of the second row indicates that there are 2 vertices in (i.e., at the extremes of) each edge; the 4 in the second column of the first row indicates that 4 edges meet at each vertex.

Projections[edit]
It is possible to project tesseracts into three- and two-dimensional spaces, similarly to projecting a cube into two-dimensional space.

Parallel projection envelopes of the tesseract (each cell is drawn with different color faces, inverted cells are undrawn)

The rhombic dodecahedron forms the convex hull of the tesseract’s vertex-first parallel-projection. The number of vertices in the layers of this projection is 1 4 6 4 1—the fourth row in Pascal’s triangle.
The cell-first parallel projection of the tesseract into three-dimensional space has a cubical envelope. The nearest and farthest cells are projected onto the cube, and the remaining six cells are projected onto the six square faces of the cube.
The face-first parallel projection of the tesseract into three-dimensional space has a cuboidal envelope. Two pairs of cells project to the upper and lower halves of this envelope, and the four remaining cells project to the side faces.
The edge-first parallel projection of the tesseract into three-dimensional space has an envelope in the shape of a hexagonal prism. Six cells project onto rhombic prisms, which are laid out in the hexagonal prism in a way analogous to how the faces of the 3D cube project onto six rhombs in a hexagonal envelope under vertex-first projection. The two remaining cells project onto the prism bases.
The vertex-first parallel projection of the tesseract into three-dimensional space has a rhombic dodecahedral envelope. Two vertices of the tesseract are projected to the origin. There are exactly two ways of dissecting a rhombic dodecahedron into four congruent rhombohedra, giving a total of eight possible rhombohedra, each a projected cube of the tesseract. This projection is also the one with maximal volume. One set of projection vectors are u=(1,1,-1,-1), v=(-1,1,-1,1), w=(1,-1,-1,1).

Animation showing each individual cube within the B4 Coxeter plane projection of the tesseract
| Coxeter plane | B4 | B4 –> A3 | A3 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | [8] | [4] | [4] |
| Coxeter plane | Other | B3 / D4 / A2 | B2 / D3 |
| Graph | 
|

|

|
| Dihedral symmetry | [2] | [6] | [4] |
|
3D Projection of three tesseracts with and without faces |
 Perspective with hidden volume elimination. The red corner is the nearest in 4D and has 4 cubical cells meeting around it. |
Tessellation[edit]
The tesseract, like all hypercubes, tessellates Euclidean space. The self-dual tesseractic honeycomb consisting of 4 tesseracts around each face has Schläfli symbol {4,3,3,4}. Hence, the tesseract has a dihedral angle of 90°.[12]
The tesseract’s radial equilateral symmetry makes its tessellation the unique regular body-centered cubic lattice of equal-sized spheres, in any number of dimensions.
Related polytopes and honeycombs[edit]
The tesseract is 4th in a series of hypercube:

|

|

|

|

|

|

|

|
| Line segment | Square | Cube | 4-cube | 5-cube | 6-cube | 7-cube | 8-cube |
The tesseract (8-cell) is the third in the sequence of 6 convex regular 4-polytopes (in order of size and complexity).
| Regular convex 4-polytopes | ||||||
|---|---|---|---|---|---|---|
| Symmetry group | A4 | B4 | F4 | H4 | ||
| Name | 5-cell
Hyper-tetrahedron |
16-cell
Hyper-octahedron |
8-cell
Hyper-cube |
24-cell
24-point |
600-cell
Hyper-icosahedron |
120-cell
Hyper-dodecahedron |
| Schläfli symbol | {3, 3, 3} | {3, 3, 4} | {4, 3, 3} | {3, 4, 3} | {3, 3, 5} | {5, 3, 3} |
| Coxeter mirrors | ||||||
| Mirror dihedrals | 𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2 | 𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2 | 𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 |
| Graph | 
|

|

|

|

|

|
| Vertices | 5 tetrahedral | 8 octahedral | 16 tetrahedral | 24 cubical | 120 icosahedral | 600 tetrahedral |
| Edges | 10 triangular | 24 square | 32 triangular | 96 triangular | 720 pentagonal | 1200 triangular |
| Faces | 10 triangles | 32 triangles | 24 squares | 96 triangles | 1200 triangles | 720 pentagons |
| Cells | 5 tetrahedra | 16 tetrahedra | 8 cubes | 24 octahedra | 600 tetrahedra | 120 dodecahedra |
| Tori | 1 5-tetrahedron | 2 8-tetrahedron | 2 4-cube | 4 6-octahedron | 20 30-tetrahedron | 12 10-dodecahedron |
| Inscribed | 120 in 120-cell | 675 in 120-cell | 2 16-cells | 3 8-cells | 25 24-cells | 10 600-cells |
| Great polygons | 2 squares x 3 | 4 rectangles x 4 | 4 hexagons x 4 | 12 decagons x 6 | 100 irregular hexagons x 4 | |
| Petrie polygons | 1 pentagon | 1 octagon | 2 octagons | 2 dodecagons | 4 30-gons | 20 30-gons |
| Long radius | 
|

|

|

|

|

|
| Edge length | 
|

|

|

|

|

|
| Short radius | 
|

|

|

|

|

|
| Area | 
|

|

|

|

|

|
| Volume | 
|

|

|

|

|

|
| 4-Content | 
|

|

|

|

|

|
As a uniform duoprism, the tesseract exists in a sequence of uniform duoprisms: {p}×{4}.
The regular tesseract, along with the 16-cell, exists in a set of 15 uniform 4-polytopes with the same symmetry. The tesseract {4,3,3} exists in a sequence of regular 4-polytopes and honeycombs, {p,3,3} with tetrahedral vertex figures, {3,3}. The tesseract is also in a sequence of regular 4-polytope and honeycombs, {4,3,p} with cubic cells.
| Orthogonal | Perspective |
|---|---|

|

|
| 4{4}2, with 16 vertices and 8 4-edges, with the 8 4-edges shown here as 4 red and 4 blue squares |
The regular complex polytope 4{4}2, ![]()
![]()
![]() , in
, in 
![]()
![]()
![]() , or 4{}×4{}, with symmetry 4[2]4, order 16. This is the symmetry if the red and blue 4-edges are considered distinct.[13]
, or 4{}×4{}, with symmetry 4[2]4, order 16. This is the symmetry if the red and blue 4-edges are considered distinct.[13]
In popular culture[edit]
Since their discovery, four-dimensional hypercubes have been a popular theme in art, architecture, and science fiction. Notable examples include:
- “And He Built a Crooked House”, Robert Heinlein’s 1940 science fiction story featuring a building in the form of a four-dimensional hypercube.[14] This and Martin Gardner’s “The No-Sided Professor”, published in 1946, are among the first in science fiction to introduce readers to the Moebius band, the Klein bottle, and the hypercube (tesseract).
- Crucifixion (Corpus Hypercubus), a 1954 oil painting by Salvador Dalí featuring a four-dimensional hypercube unfolded into a three-dimensional Latin cross.[15]
- The Grande Arche, a monument and building near Paris, France, completed in 1989. According to the monument’s engineer, Erik Reitzel, the Grande Arche was designed to resemble the projection of a hypercube.[16]
- Fez, a video game where one plays a character who can see beyond the two dimensions other characters can see, and must use this ability to solve platforming puzzles. Features “Dot”, a tesseract who helps the player navigate the world and tells how to use abilities, fitting the theme of seeing beyond human perception of known dimensional space.[17]
The word tesseract was later adopted for numerous other uses in popular culture, including as a plot device in works of science fiction, often with little or no connection to the four-dimensional hypercube. See Tesseract (disambiguation).
See also[edit]
- Mathematics and art
Notes[edit]
- ^ “The Tesseract – a 4-dimensional cube”. www.cut-the-knot.org. Retrieved 2020-11-09.
- ^ Matila Ghyka, The geometry of Art and Life (1977), p.68
- ^ This term can also mean a polycube made of four cubes
- ^ Elte, E. L. (1912). The Semiregular Polytopes of the Hyperspaces. Groningen: University of Groningen. ISBN 1-4181-7968-X.
- ^ Coxeter 1973, pp. 122–123, §7.2. illustration Fig 7.2C.
- ^
“tesseract”. Oxford English Dictionary (Online ed.). Oxford University Press. 199669. (Subscription or participating institution membership required.) - ^ “Unfolding an 8-cell”. Unfolding.apperceptual.com. Retrieved 21 January 2018.
- ^ Coxeter 1970, p. 18.
- ^ Pournin, Lionel (2013), “The flip-Graph of the 4-dimensional cube is connected”, Discrete & Computational Geometry, 49 (3): 511–530, arXiv:1201.6543, doi:10.1007/s00454-013-9488-y, MR 3038527, S2CID 30946324
- ^ Cottle, Richard W. (1982), “Minimal triangulation of the 4-cube”, Discrete Mathematics, 40: 25–29, doi:10.1016/0012-365X(82)90185-6, MR 0676709
- ^ Coxeter 1973, p. 12, §1.8 Configurations.
- ^ Coxeter 1973, p. 293.
- ^ Coxeter, H. S. M., Regular Complex Polytopes, second edition, Cambridge University Press, (1991).
- ^ Fowler, David (2010), “Mathematics in Science Fiction: Mathematics as Science Fiction”, World Literature Today, 84 (3): 48–52, doi:10.1353/wlt.2010.0188, JSTOR 27871086, S2CID 115769478
- ^ Kemp, Martin (1 January 1998), “Dali’s dimensions”, Nature, 391 (27): 27, Bibcode:1998Natur.391…27K, doi:10.1038/34063, S2CID 5317132
- ^ Ursyn, Anna (2016), “Knowledge Visualization and Visual Literacy in Science Education”, Knowledge Visualization and Visual Literacy in Science Education, Information Science Reference, p. 91, ISBN 9781522504818
- ^ “Dot (Character) – Giant Bomb”. Giant Bomb. Retrieved 21 January 2018.
References[edit]
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover. pp. 122–123.
- F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss (1995) Kaleidoscopes: Selected Writings of H.S.M. Coxeter, Wiley-Interscience Publication ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, Mathematische Zeitschrift 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Coxeter, H.S.M. (1970), “Twisted Honeycombs”, Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, Providence, Rhode Island: American Mathematical Society, 4
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1n1)
- T. Gosset (1900) On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan.
- T. Proctor Hall (1893) “The projection of fourfold figures on a three-flat”, American Journal of Mathematics 15:179–89.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Victor Schlegel (1886) Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper, Waren.
External links[edit]
- Weisstein, Eric W. “Tesseract”. MathWorld.
- Klitzing, Richard. “4D uniform polytopes (polychora) x4o3o3o – tes”.
- The Tesseract Ray traced images with hidden surface elimination. This site provides a good description of methods of visualizing 4D solids.
- Der 8-Zeller (8-cell) Marco Möller’s Regular polytopes in ℝ4 (German)
- WikiChoron: Tesseract
- HyperSolids is an open source program for the Apple Macintosh (Mac OS X and higher) which generates the five regular solids of three-dimensional space and the six regular hypersolids of four-dimensional space.
- Hypercube 98 A Windows program that displays animated hypercubes, by Rudy Rucker
- ken perlin’s home page A way to visualize hypercubes, by Ken Perlin
- Some Notes on the Fourth Dimension includes animated tutorials on several different aspects of the tesseract, by Davide P. Cervone
- Tesseract animation with hidden volume elimination
Fundamental convex regular and uniform polytopes in dimensions 2–10 |
|||||
|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn |
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon |
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | |
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell |
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | ||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | |
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | |
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | |
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | ||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | ||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope |
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds |
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 ноября 2017;
проверки требуют 23 правки.

| Тессеракт | |
|---|---|

|
|
| Тип | Правильный четырёхмерный политоп |
| Символ Шлефли | {4,3,3} |
| Ячеек | 8 |
| Граней | 24 |
| Рёбер | 32 |
| Вершин | 16 |
| Вершинная фигура | Правильный тетраэдр |
| Двойственный политоп | 16-ячейник |

Анимированная проекция вращающегося тессеракта
Тессера́кт (от др.-греч. τέσσαρες ἀκτῖνες «четыре луча») — четырёхмерный гиперкуб — куб в четырёхмерном пространстве. Другие названия: 4-куб, тетраку́б (от др.-греч. τέτταρες «четыре»), восьмияче́йник[1], октахо́р (от др.-греч. οκτώ «восемь» + χώρος «место, пространство»), гиперкуб (если число измерений не оговаривается).
Согласно Оксфордскому словарю, слово tesseract было придумано Чарльзом Говардом Хинтоном (1853–1907) и впервые использовано в 1888 году в его книге «Новая эра мысли».
Содержание
- 1 Геометрия
- 2 Популярное описание
- 3 Развёртки тессеракта
- 4 Проекции
- 4.1 На двумерное пространство
- 4.2 На трёхмерное пространство
- 4.3 Стереопара
- 5 Тессеракт в культуре
- 6 Примечания
- 7 Литература
- 8 Ссылки
Геометрия[править | править код]
Обычный тессеракт в евклидовом четырёхмерном пространстве определяется как выпуклая оболочка точек (±1, ±1, ±1, ±1). Иначе говоря, он может быть представлен в виде следующего множества:
Тессеракт ограничен восемью гиперплоскостями 
Четырёхмерный гиперобъём тессеракта со стороной длиной a рассчитывается по формуле:

Объём же гиперповерхности тессеракта можно найти по формуле:

Радиус описанной гиперсферы:

Радиус вписанной гиперсферы:

Популярное описание[править | править код]
Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из трёхмерного пространства.
В одномерном «пространстве» — на линии — выделим отрезок АВ длиной L.
На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат CDBA. Повторив эту операцию с плоскостью, получим трёхмерный куб CDBAGHFE. А сдвинув куб в четвёртом измерении (перпендикулярно первым трём) на расстояние L, мы получим гиперкуб CDBAGHFEKLJIOPNM.
Построение тессеракта на плоскости

Развёртка тессеракта
Одномерный отрезок АВ служит стороной двумерного квадрата CDBA, квадрат — стороной куба CDBAGHFE, который, в свою очередь, будет стороной четырёхмерного гиперкуба. Отрезок прямой имеет две граничные точки, квадрат — четыре вершины, куб — восемь. В четырёхмерном гиперкубе, таким образом, окажется 16 вершин: 8 вершин исходного куба и 8 сдвинутого в четвёртом измерении. Он имеет 32 ребра — по 12 дают начальное и конечное положения исходного куба, и ещё 8 рёбер «нарисуют» восемь его вершин, переместившихся в четвёртое измерение. Те же рассуждения можно проделать и для граней гиперкуба. В двумерном пространстве она одна (сам квадрат), у куба их 6 (по две грани от переместившегося квадрата и ещё четыре опишут его стороны). Четырёхмерный гиперкуб имеет 24 квадратные грани — 12 квадратов исходного куба в двух положениях и 12 квадратов от двенадцати его рёбер.
Как сторонами квадрата являются 4 одномерных отрезка, а сторонами (гранями) куба являются 6 двухмерных квадратов, так и для «четырёхмерного куба» (тессеракта) сторонами являются 8 трёхмерных кубов. Пространства противоположных пар кубов тессеракта (то есть трёхмерные пространства, которым эти кубы принадлежат) параллельны. На рисунке это кубы: CDBAGHFE и KLJIOPNM, CDBAKLJI и GHFEOPNM, EFBAMNJI и GHDCOPLK, CKIAGOME и DLJBHPNF.
Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трёхмерного пространства, будет выглядеть четырёхмерный гиперкуб. Воспользуемся для этого уже знакомым методом аналогий.
Возьмём проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединённые четырьмя линиями — боковыми рёбрами. Аналогичным образом четырёхмерный гиперкуб в пространстве трёх измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединённых восемью рёбрами. При этом сами «ящики» — трёхмерные грани — будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в направлении четвёртой оси. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.
Подобно тому, как трёхмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвёртое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Сам же четырёхмерный гиперкуб состоит из бесконечного количества кубов, подобно тому как трёхмерный куб можно «нарезать» на бесконечное количество плоских квадратов.
Разрезав шесть граней трёхмерного куба, можно разложить его в плоскую фигуру — развёртку. Она будет иметь по квадрату с каждой стороны исходной грани плюс ещё один — грань, ей противоположную. А трёхмерная развёртка четырёхмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс ещё одного — конечной «гиперграни».
Свойства тессеракта представляют собой продолжение свойств геометрических фигур меньшей размерности в четырёхмерное пространство.
Развёртки тессеракта[править | править код]

Разворачивание поверхности тессеракта в трёхмерное пространство
Аналогично тому, как поверхность куба может быть развёрнута в многоугольник, состоящий из шести квадратов, поверхность тессеракта может быть развёрнута в трёхмерное тело, состоящее из восьми кубов[2].
Существует 261 развёртка тессеракта[3].
Развёртки гиперкуба могут быть найдены перечислением «сдвоенных деревьев», где «сдвоенное дерево» (paired tree) — это дерево с чётным числом вершин, которые разбиты на пары так, что ни одна пара не состоит из двух смежных вершин. Между «сдвоенными деревьями» с 8 вершинами и развёртками тессеракта существует взаимно однозначное соответствие. Всего существует 23 дерева с 8 вершинами, при разбиении вершин которых на пары несмежных вершин получается 261 «сдвоенное дерево» с 8 вершинами[4].
Крестообразная развёртка тессеракта является элементом картины Сальвадора Дали «Corpus Hypercubus» (1954)[5].
В рассказе Роберта Хайнлайна «Дом, который построил Тил» («—And He Built a Crooked House») калифорнийский архитектор Квинтус Тил строит дом в форме развёртки гиперкуба, который во время землетрясения складывается в четырёхмерный тессеракт[5].
Проекции[править | править код]
На двумерное пространство[править | править код]
Данная структура сложна для воображения, но возможно спроектировать тессеракт в двумерные или трёхмерные пространства. Кроме того, проецирование на плоскость позволяет легко понять расположение вершин гиперкуба. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения в пределах тессеракта, но которые иллюстрируют структуру связи вершин, как в следующих примерах:
|
Первая картинка показывает, как тессеракт получен в результате комбинирования двух кубов. Схема подобна построению куба от двух квадратов |
Вторая картинка иллюстрирует тот факт, что все рёбра тессеракта имеют одинаковую длину. Она примечательна тем, что все восемь кубов имеют одинаковый вид. |
Третья картинка демонстрирует тессеракт в изометрии, относительно точки построения. Это изображение представляет интерес при использовании тессеракта как основания для топологической сети, чтобы связать многократные процессоры в параллельных вычислениях. |
На трёхмерное пространство[править | править код]

Вращающаяся модель тессеракта. Эта модель показывает грани тессеракта — равные кубы
Одна из проекций тессеракта на трёхмерное пространство представляет собой два вложенных трёхмерных куба, соответствующие вершины которых соединены между собой отрезками.
Внутренний и внешний кубы имеют разные размеры в трёхмерном пространстве, но в четырёхмерном пространстве это равные кубы. Для понимания равности всех кубов тессеракта была создана вращающаяся модель тессеракта.
- Шесть усечённых пирамид по краям тессеракта — это изображения равных шести кубов. Однако эти кубы для тессеракта — как квадраты (грани) для куба. Но на самом деле тессеракт можно разделить на бесконечное количество кубов, как куб — на бесконечное количество квадратов, или квадрат — на бесконечное число отрезков.
Ещё одна интересная проекция тессеракта на трёхмерное пространство представляет собой ромбододекаэдр с проведёнными четырьмя его диагоналями, соединяющими пары противоположных вершин при больших углах ромбов. При этом 14 из 16 вершин тессеракта проецируются в 14 вершин ромбододекаэдра, а проекции 2 оставшихся совпадают в его центре. В такой проекции на трёхмерное пространство сохраняются равенство и параллельность всех одномерных, двухмерных и трёхмерных сторон.
Стереопара[править | править код]
Стереопара тессеракта изображается как две проекции на плоскость одного из вариантов трёхмерного представления тессеракта. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопический эффект, позволяющий лучше воспринять проекцию тессеракта на трёхмерное пространство.

Тессеракт в культуре[править | править код]
- В одном эпизоде «Приключений Джимми Нейтрона» «мальчик-гений» Джимми изобретает четырёхмерный гиперкуб, идентичный фолдбоксу из романа «Дорога славы» (1963) Роберта Хайнлайна.
- В романе «Дорога славы» Хайнлайна описана гиперразмерная шкатулка, которая была изнутри больше, чем снаружи.
- В рассказе «…И построил он себе скрюченный домишко» (в другом варианте перевода «Дом, который построил Тил») Хайнлайна описан восьмикомнатный дом в форме развёрнутого тессеракта.
- Рассказ Генри Каттнера «Все тенали бороговы» описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.
- В романе Алекса Гарленда «Тессеракт» 1999 года, термин «тессеракт» используется для трёхмерной развёртки четырёхмерного гиперкуба, а не гиперкуба непосредственно. Это метафора, призванная показать, что познающая система должна быть шире познаваемой.
- Сюжет фильма «Куб 2: Гиперкуб» сосредотачивается на восьми незнакомцах, пойманных в ловушку в «гиперкубе», или сети связанных трёхмерных проекций одного «гиперкуба».
- В серии фильмов «Кинематографическая вселенная Marvel» Тессеракт — это ключевой элемент сюжета, космический артефакт в форме гиперкуба.
- Сюжет фильма «Мстители» сосредоточен на использовании куба «Тессеракт» как неиссякаемого источника космической энергии, для открытия портала в другое «измерение» с целью осуществления плана по захвату мира (в обмен на Тессеракт — читаури предоставят Локи армию для захвата Земли). Однако этот материал не имеет почти ничего общего с общей теории четырех измерений.
- В комиксе «Дэдпул уничтожает Вселенную Marvel» главный герой при помощи суперзлодея Аркады использует тессеракт, чтобы поймать Китти Прайд: её способности не смогли ей помочь выйти из куба.
- Телесериал «Андромеда» использует тессеракт-генераторы как устройство заговора. Они прежде всего предназначены, чтобы управлять пространством и временем.
- Кресты на некоторых христианских храмах и монастырях Египта напоминают развертку тессеракта.
- Комиксы «Nextwave comic book» изображают средство передвижения, включающее в себя 5 зон тессеракта.
- В альбоме «Voivod» «Nothingface» одна из композиций названа «В моём гиперкубе».
- В романе Энтони Пирса «Маршрут Куба» одна из орбитальных лун Международной ассоциации развития называется тессерактом, который был сжат в 3 измерения.
- В сериале «Школа „Чёрная дыра“» в третьем сезоне есть серия «Тессеракт». Лукас нажимает на секретную кнопку, и школа начинает «складываться, как математический тессеракт».
- Термин «тессеракт» и производный от него термин «тессировать» встречается в повести Мадлен Л’Энгл «Складка времени».
- «TesseracT» — название британской джент-группы.
- В рассказе Роберта Шекли «Мисс Мышка и четвёртое измерение» писатель-эзотерик, знакомец автора, пытается увидеть тессеракт, часами глядя на сконструированный им прибор: шар на ножке с воткнутыми в него стержнями, на которые насажены кубы, обклеенные всеми подряд эзотерическими символами. В рассказе упоминается труд Хинтона.
- В инди-игре «Fez» Дот — компаньон главного героя — является тессерактом.
- Во вселенной «Warhammer 40000» некроны используют технологию «карманных измерений», чтобы заключать осколки К’Тан в тессерактовые лабиринты — бесконечный лабиринт-тюрьму.
- В аниме «Евангелион 3.33: Ты (не) исправишь» Ева-01 была заключена в развёрнутый тессеракт на орбите Земли.
- В серии «Настоящий ты» из мультфильма «Время приключений» в виде 4-мерного мыльного пузыря
- В фантастическом рассказе Марка Клифтона «На ленте Мёбиуса» дети-вундеркинды путешествуют через пространство и время, используя модели ленты Мёбиуса, бутылки Клейна и тессеракта.
- В 11-й серии аниме «Space Dandy» показана подруга главного героя Катрин, которая является тессерактом.
- В инди-игре «The Bridge» тессеракт появляется после прохождения всех уровней в нормальном мире.
Примечания[править | править код]
- ↑ Д. К. Бобылёв. Четырехмерное пространство // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- ↑ Gardner, 1989, pp. 48-50.
- ↑ Gardner, 1989, p. 272: «Peter Turney, in his 1984 paper „Unfolding the Tesseract“, uses graph theory to show that there are 261 distinct unfoldings.».
- ↑ Peter Turney (1984–85). “Unfolding the Tesseract”. Journal of Recreational Mathematics. 17 (1).
- ↑ 1 2 Gardner, 1989, p. 50.
Литература[править | править код]
- Charles H. Hinton. Fourth Dimension, 1904. ISBN 0-405-07953-2
- Gardner M. Mathematical Carnival. — Washington, D.C.: MAA, 1989. — P. 41-54, 272. — ISBN 0-88385-448-1.
- Ian Stewart, Concepts of Modern Mathematics, 1995. ISBN 0-486-28424-7
- Гальперин Г.А. Многомерный куб. — М.: МЦНМО, 2015. — 80 с. — ISBN 978-5-4439-0296-8.
- Дужин С., Рубцов В. Четырехмерный куб // Квант. — 1986. — № 6. — С. 3-7.
Ссылки[править | править код]
- На русском языке
- Получение из развертки
- Гиперкуб
- Программа Transformator4D. Формирование моделей трёхмерных проекций четырёхмерных объектов (в том числе и Гиперкуба).
- Программа, реализующая построение тессеракта и все его афинные преобразования, с исходниками на С++.
- Стереопара тессеракта с ребрами одинаковой длины.
- Вращение тессеракта – проекция в трёхмерном пространстве
- На английском языке
- Tesseract
- Cut The Knot! The Tesseract
- Charles Howard Hinton
- A four dimensional version of Rubik’s Cube
- Fourth Dimension: Tetraspace
- Mushware Limited — программа вывода тессеракта (Tesseract Trainer, лицензия совместима с GPLv2) и шутер от первого лица в четырёхмерном пространстве (Adanaxis; графика, в основном, трёхмерная; есть версия под GPL в репозиториях ОС).
| Основные выпуклые правильные и однородные политопы в размерностях 2-10 | |||||
|---|---|---|---|---|---|
| Семейство | An | Bn | I₂(p) / Dn | E₆ / E₇ / E₈ / F₄ / G₂ | H₄ |
| Правильный многоугольник | Правильный треугольник | Квадрат | p-gon | Правильный шестиугольник | Правильный пятиугольник |
| Однородный многогранник | Правильный тетраэдр | Правильный октаэдр • Куб | Полукуб | Правильный додекаэдр • Правильный икосаэдр | |
| Однородный 4-политоп | Пятиячейник | 16-ячейник • Тессеракт | Полутессеракт | 24-ячейник | 120-ячейник • 600-ячейник |
| Однородный 5-политоп | Правильный 5-симплекс | 5-ортоплекс • 5-гиперкуб | 5-полугиперкуб | ||
| Однородный 6-политоп | Правильный 6-симплекс | 6-ортоплекс • 6-гиперкуб | 6-полугиперкуб | 122 • 221 | |
| Однородный 7-политоп | Правильный 7-симплекс | 7-ортоплекс • 7-гиперкуб | 7-полугиперкуб | 132 • 231 • 321 | |
| Однородный 8-политоп | Правильный 8-симплекс | 8-ортоплекс • 8-гиперкуб | 8-полугиперкуб | 142 • 241 • 421 | |
| Однородный 9-политоп | Правильный 9-симплекс | 9-ортоплекс • 9-гиперкуб | 9-полугиперкуб | ||
| Однородный 10-политоп | Правильный 10-симплекс | 10-ортоплекс • 10-гиперкуб | 10-полугиперкуб | ||
| Однородный n-политоп | Правильный n-симплекс | n-ортоплекс • n-гиперкуб | n-полугиперкуб | 1k2 • 2k1 • k21 | n-Пятиугольный многогранник |
| Topics: Семейства политопов • Правильные политопы • Список правильных политопов и их соединений |
![[-1, 1]^4 equiv {(x_1,x_2,x_3,x_4) ,:, -1 leq x_i leq 1 }.](https://wikimedia.org/api/rest_v1/media/math/render/svg/665becf62e2d86571b1bd369e56a104356f43080)





![[-1, 1]^4 equiv {(x_1,x_2,x_3,x_4) ,:, -1 leq x_i leq 1 }.](https://web.archive.org/web/20190425181410im_/https://wikimedia.org/api/rest_v1/media/math/render/svg/665becf62e2d86571b1bd369e56a104356f43080)




