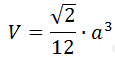Объём тетраэдра онлайн калькулятор
Онлайн калькулятор вычиселения объема тетраэдра поможет вычислить объем тетраэдра различными способами:
- По длине одного ребра.
- По площади основания и высоте.
Объем тетраэдра можно вычислить на этом онлайн калькуляторе.Вы получите ответ в развернутом виде шаг за шагом. Тем самым усвоете материал по данной теме.
- Калькулятор
- Инструкция
- Теория
- История
- Сообщить о проблеме

Способ расчета обьема тетраэдра:
Длина ребра а:
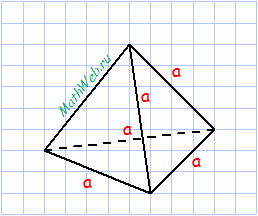
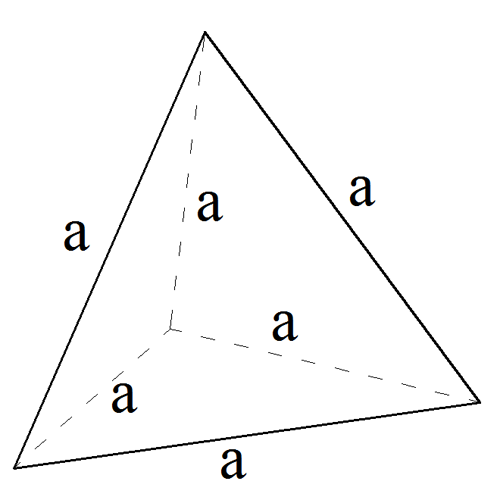
Тетраэдр — простейший многогранник, гранями которого являются четыре треугольника.
Формула объёма тетраэдра:
гда а – длина ребра тетраэдра
Решение:
V =
√2
12
· a3
=
√2
12
· 1.63
=
√2
12
· 4.096
=
0.481
Ответ: Объём тетраэдра с длиной ребра а = 1.6 равен 0.481
Тетраэдр является треугольной пирамидой при принятии любой из граней за основание.
У тетраэдра 4 грани, 4 вершины и 6 рёбер. Тетраэдр, у которого все грани — равносторонние треугольники, называется правильным.
Правильный тетраэдр является одним из пяти правильных многогранников.
Похожие калькуляторы
-
Объём цилиндра онлайн калькулятор (3 способа)
-
Объём пирамиды онлайн калькулятор
-
Объём шара онлайн калькулятор (3 способа)
-
Объём призмы онлайн калькулятор
-
Объём параллелепипеда онлайн калькулятор (3 способа)
Калькуляторы других категорий
-
Деление в столбик онлайн. Калькулятор наглядного деления.
-
Сторона треугольника 14 формул расчет онлайн
-
Перевод чисел из одной системы счисления в любую другую онлайн
-
Сложение, умножение и деление чисел в различных системах счисления
-
Умножение в столбик онлайн. Калькулятор наглядного умножения.
| Ваша оценка? |
Тетраэдр – простейшее многогранное тело, гранями и основанием которого являются треугольники.
Онлайн-калькулятор объема тетраэдра
Тетраэдр имеет четыре грани, каждая их которых образована тремя сторонами. Вершин у тетраэдра четыре, из каждой выходит по три ребра.
Данное тело разделяется на несколько видов. Ниже приведена их классификация.
- Равногранный тетраэдр — у него все грани являются одинаковыми треугольниками;
- Ортоцентрический тетраэдр — все высоты, проведенные из каждой вершины на противолежащую грань, являются одинаковыми по длине;
- Прямоугольный тетраэдр — ребра, исходящие из одной вершины, образуют друг с другом угол в 90 градусов;
- Каркасный;
- Соразмерный;
- Инцентрический.
Формулы объема тетраэдра
Объем данного тела можно найти несколькими способами. Разберем их более подробно.
Через смешанное произведение векторов
Если тетраэдр построен на трех векторах с координатами:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем этого тетраэдра это смешанное произведение этих векторов, то есть такой определитель:
V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Известны координаты четырех вершин октаэдра. A(1,4,9)A(1,4,9), B(8,7,3)B(8,7,3), C(1,2,3)C(1,2,3), D(7,12,1)D(7,12,1). Найдите его объем.
Решение
A(1,4,9)A(1,4,9)
B(8,7,3)B(8,7,3)
C(1,2,3)C(1,2,3)
D(7,12,1)D(7,12,1)
Первым шагом является определение координат векторов, на которых построено данное тело.
Для этого необходимо найти каждую координату вектора путем вычитания соответствующих координат двух точек. Например, координаты вектора AB→overrightarrow{AB}, то есть, вектора, направленного от точки AA к точке BB, это разности соответствующих координат точек BB и AA:
AB→=(8−1,7−4,3−9)=(7,3,−6)overrightarrow{AB}=(8-1, 7-4, 3-9)=(7, 3, -6)
Далее, аналогично:
AC→=(1−1,2−4,3−9)=(0,−2,−6)overrightarrow{AC}=(1-1, 2-4, 3-9)=(0, -2, -6)
AD→=(7−1,12−4,1−9)=(6,8,−8)overrightarrow{AD}=(7-1, 12-4, 1-9)=(6, 8, -8)
Теперь найдем смешанное произведение данных векторов, для этого составим определитель третьего порядка, при этом принимая, что AB→=a⃗overrightarrow{AB}=vec{a}, AC→=b⃗overrightarrow{AC}=vec{b}, AD→=c⃗overrightarrow{AD}=vec{c}.
∣axayazbxbybzcxcycz∣=∣73−60−2−668−8∣=7⋅(−2)⋅(−8)+3⋅(−6)⋅6+(−6)⋅0⋅8−(−6)⋅(−2)⋅6−7⋅(−6)⋅8−3⋅0⋅(−8)=112−108−0−72+336+0=268begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}=
begin{vmatrix}
7 & 3 & -6 \
0 & -2 & -6 \
6 & 8 & -8 \
end{vmatrix}=7cdot(-2)cdot(-8) + 3cdot(-6)cdot6 + (-6)cdot0cdot8 – (-6)cdot(-2)cdot6 – 7cdot(-6)cdot8 – 3cdot0cdot(-8) = 112 – 108 – 0 – 72 + 336 + 0 = 268
То есть, объем тетраэдра равен:
V=16⋅∣axayazbxbybzcxcycz∣=16⋅∣73−60−2−668−8∣=16⋅268≈44.8 см3V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}=frac{1}{6}cdot
begin{vmatrix}
7 & 3 & -6 \
0 & -2 & -6 \
6 & 8 & -8 \
end{vmatrix}=frac{1}{6}cdot268approx44.8text{ см}^3
Ответ
44.8 см3.44.8text{ см}^3.
Формула объема равногранного тетраэдра по его стороне
Эта формула справедлива только для вычисления объема равногранного тетраэдра, то есть такого тетраэдра, у которого все грани являются одинаковыми правильными треугольниками.
V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}
aa — длина ребра тетраэдра.
Определить объем тетраэдра, если дана его сторона, равная 11 см11text{ см}.
Решение
a=11a=11
Подставляем aa в формулу для объема тетраэдра:
V=2⋅a312=2⋅11312≈156.8 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 11^3}{12}approx156.8text{ см}^3
Ответ
156.8 см3.156.8text{ см}^3.
На нашем сайте вы можете оформить выполнение контрольных работ на заказ онлайн!
Тест по теме «Объем тетраэдра»
Через объем тетраэдра можно узнать ребро, как единственное звено, от которого зависят все вычисления параметров тетраэдра. Ребро тетраэдра будет равно шести корням из двух, умноженных на объем по кубическим корнем.
a=∛(6√2 V)
Рассчитав таким образом ребро тетраэдра, можно узнать его периметр, площадь одной грани и площадь полной поверхности тетраэдра соответственно.
P=6a=6∛(6√2 V)
S_1=√3/2 ∛(9V^2 )
S_(п.п.)=4S_1=2∛(9V^2 )
Радиус вписанной и описанной окружности вокруг одной из граней-основания тетраэдра вычисляется подстановкой вместо ребра тетраэдра кубического корня, выраженного через объем.
r=a/(2√3)=∛(√2/(4√3) V)
R=a/√3=∛((2√2)/√3 V)
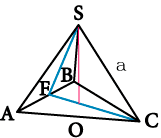
Объемные параметры тетраэдра, такие как высота тетраэдра и апофема тетраэдра, можно рассчитать через объем вместо ребра, заменив последнее на соответствующее выражение. (рис. 60.1)
h=√(2/3) a=2∛(V/√3)
l=(√3 a)/2=2√6 ∛3V
Радиусы вписанной и описанной сфер около тетраэдра также можно представить в виде выражения, зависящего от объема тетраэдра вместо ребра. (рис.60.2, 60.3)
r_1=a/(2√6)=∛V/(2∛(3 ))
R_1=(√3 a)/(2√2)=(√3 ∛3V)/2
Объем тетраэдра – характеристика геометрической фигуры, имеющей 3 равные плоскости треугольной формы.
Все ребра данной объемной фигуры равны. Если в онлай калькуляторе задать в соответствующем поле формы в качестве исходных данных длину ребра тетраэдра, программный скрипт вычислит объем тетраэдра, воспользовавшись формулой: V = (sqrt (2)/12) х a3.
Тетраэдр используется при создании весьма практичной пользовательской тары, в частности пакета для молока. Ценность подобной тары заключается в ее максимально полном заполнении предназначенного для грузоперевозки пространства автотранспортного средства. Зная ребро данного компактного пакета можно вычислить объем его содержимого. Вычисление объема тетраэдра может быть полезно в инженерных расчетах проектирования сложных оптических устройств.
Вам помог этот калькулятор?
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Это помогает делать новые калькуляторы.
НЕТ
Объём правильного тетраэдра онлайн
Значащих цифр:
Введите длину ребра
Формула объёма тетраэдра
Формула объёма правильного тетраэдра через длину ребра
{V = Largefrac{{a^3}sqrt{2}}{12}}
Определение правильного тетраэдра
Правильный тетраэдр это треугольная пирамида у которой все грани равны и являются равносторонними треугольниками.
Свойства правильного тетраэдра
Все длины рёбер тетраэдра равны
Все 4 стороны являются равными равносторонними треугольниками.
Найти объём тетраэдра с ребром 8
Найти объём тетраэдра с ребром 35
Найти объём тетраэдра с ребром 17
Найти объём тетраэдра с ребром 23
Найти объём тетраэдра с ребром 8
Найти объём тетраэдра с ребром 6