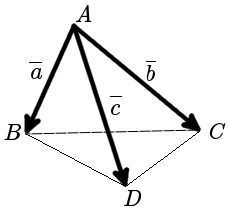
Тетраэдр – простейшее многогранное тело, гранями и основанием которого являются треугольники.
Онлайн-калькулятор объема тетраэдра
Тетраэдр имеет четыре грани, каждая их которых образована тремя сторонами. Вершин у тетраэдра четыре, из каждой выходит по три ребра.
Данное тело разделяется на несколько видов. Ниже приведена их классификация.
- Равногранный тетраэдр — у него все грани являются одинаковыми треугольниками;
- Ортоцентрический тетраэдр — все высоты, проведенные из каждой вершины на противолежащую грань, являются одинаковыми по длине;
- Прямоугольный тетраэдр — ребра, исходящие из одной вершины, образуют друг с другом угол в 90 градусов;
- Каркасный;
- Соразмерный;
- Инцентрический.
Формулы объема тетраэдра
Объем данного тела можно найти несколькими способами. Разберем их более подробно.
Через смешанное произведение векторов
Если тетраэдр построен на трех векторах с координатами:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем этого тетраэдра это смешанное произведение этих векторов, то есть такой определитель:
V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Известны координаты четырех вершин октаэдра. A(1,4,9)A(1,4,9), B(8,7,3)B(8,7,3), C(1,2,3)C(1,2,3), D(7,12,1)D(7,12,1). Найдите его объем.
Решение
A(1,4,9)A(1,4,9)
B(8,7,3)B(8,7,3)
C(1,2,3)C(1,2,3)
D(7,12,1)D(7,12,1)
Первым шагом является определение координат векторов, на которых построено данное тело.
Для этого необходимо найти каждую координату вектора путем вычитания соответствующих координат двух точек. Например, координаты вектора AB→overrightarrow{AB}, то есть, вектора, направленного от точки AA к точке BB, это разности соответствующих координат точек BB и AA:
AB→=(8−1,7−4,3−9)=(7,3,−6)overrightarrow{AB}=(8-1, 7-4, 3-9)=(7, 3, -6)
Далее, аналогично:
AC→=(1−1,2−4,3−9)=(0,−2,−6)overrightarrow{AC}=(1-1, 2-4, 3-9)=(0, -2, -6)
AD→=(7−1,12−4,1−9)=(6,8,−8)overrightarrow{AD}=(7-1, 12-4, 1-9)=(6, 8, -8)
Теперь найдем смешанное произведение данных векторов, для этого составим определитель третьего порядка, при этом принимая, что AB→=a⃗overrightarrow{AB}=vec{a}, AC→=b⃗overrightarrow{AC}=vec{b}, AD→=c⃗overrightarrow{AD}=vec{c}.
∣axayazbxbybzcxcycz∣=∣73−60−2−668−8∣=7⋅(−2)⋅(−8)+3⋅(−6)⋅6+(−6)⋅0⋅8−(−6)⋅(−2)⋅6−7⋅(−6)⋅8−3⋅0⋅(−8)=112−108−0−72+336+0=268begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}=
begin{vmatrix}
7 & 3 & -6 \
0 & -2 & -6 \
6 & 8 & -8 \
end{vmatrix}=7cdot(-2)cdot(-8) + 3cdot(-6)cdot6 + (-6)cdot0cdot8 – (-6)cdot(-2)cdot6 – 7cdot(-6)cdot8 – 3cdot0cdot(-8) = 112 – 108 – 0 – 72 + 336 + 0 = 268
То есть, объем тетраэдра равен:
V=16⋅∣axayazbxbybzcxcycz∣=16⋅∣73−60−2−668−8∣=16⋅268≈44.8 см3V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}=frac{1}{6}cdot
begin{vmatrix}
7 & 3 & -6 \
0 & -2 & -6 \
6 & 8 & -8 \
end{vmatrix}=frac{1}{6}cdot268approx44.8text{ см}^3
Ответ
44.8 см3.44.8text{ см}^3.
Формула объема равногранного тетраэдра по его стороне
Эта формула справедлива только для вычисления объема равногранного тетраэдра, то есть такого тетраэдра, у которого все грани являются одинаковыми правильными треугольниками.
V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}
aa — длина ребра тетраэдра.
Определить объем тетраэдра, если дана его сторона, равная 11 см11text{ см}.
Решение
a=11a=11
Подставляем aa в формулу для объема тетраэдра:
V=2⋅a312=2⋅11312≈156.8 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 11^3}{12}approx156.8text{ см}^3
Ответ
156.8 см3.156.8text{ см}^3.
На нашем сайте вы можете оформить выполнение контрольных работ на заказ онлайн!
Тест по теме «Объем тетраэдра»
Рассмотрим произвольный треугольник ABC и точку D, не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC. В результате получим треугольники ADC, CDB, ABD. Поверхность ограниченная четырьмя треугольниками ABC, ADC, CDB и ABD называется тетраэдром и обозначается DABC.

Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра
Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.
Таким образом, тетраэдр – это простейший многогранник, гранями которого являются четыре треугольника.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле

где
- S – площадь любой грани,
- H – высота, опущенная на эту грань
Правильный тетраэдр – частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:
- Все грани равны.
- Все плоские углы правильного тетраэдра равны 60°
- Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
- Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).
Пусть нам дан правильный тетраэдр ABCD с ребрами равными a. DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD.
Высота BM равна BM и равна
Рассмотрим треугольник BDM, где DH, являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

BM=

p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим
Вынесем 1/2a. Получим
Применим формулу разность квадратов

После небольших преобразований получим

Объем любого тетраэдра можно рассчитать по формуле

где 

Подставив эти значения, получим
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра
Вычисление объема тетраэдра, если известны координаты его вершин
Пусть нам даны координаты вершин тетраэдра
Из вершины 



Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим


Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула

Для закрепления материала рассмотрим пример использования формулы объема тетраэдра.
Объем правильного тетраэдра равен 2 см3. Найдите объем правильного тетраэдра, ребро которого в 3 раза больше ребра данного тетраэдра.
Объем правильного тетраэдра вычисляется по формуле
Тогда
Выразим куб стороны
Если сторону увеличить в 3 раза, что его куб увеличиться в 27 раз. Тогда

Найдем объем 
Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.
Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал.
Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Выберите каким образом задается пирамида (тетраэдр):
Введите значения векторов: Введите координаты вершин пирамиды:
Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
- Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.
Теория. Объем пирамиды (объем тетраэдра) построенной на векторах
Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Объем треугольной пирамиды (тетраэдра), построенной на векторах онлайн
Объём треугольной пирамиды (тетраэдра) равен (1/6) от величины смешанного произведения векторов на которых она построена:
Так как значение смешанного произведения векторов может быть числом отрицательным, а объём тетраэдра – только положительным, то при вычислении объёма треугольной пирамиды (тетраэдра), построенной на векторах, результат смешанного произведения берется по модулю:
Вычислить объём треугольной пирамиды (тетраэдра), построенной на векторах поможет наш онлайн калькулятор с описанием хода решения на русском языке.
Объем тетраэдра
Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC . 
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра
Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
- S – площадь любой грани,
- H – высота, опущенная на эту грань
Правильный тетраэдр – частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:
- Все грани равны.
- Все плоские углы правильного тетраэдра равны 60°
- Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
- Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).
Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна 
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

BM=

p=1/2 (BM+BD+DM)= 
Подставим эти значения в формулу высоты. Получим 
Вынесем 1/2a. Получим


Применим формулу разность квадратов

После небольших преобразований получим


Объем любого тетраэдра можно рассчитать по формуле 
где 

Подставив эти значения, получим
Таким образом формула объема для правильного тетраэдра
где a –ребро тетраэдра
Вычисление объема тетраэдра, если известны координаты его вершин
Пусть нам даны координаты вершин тетраэдра 
Из вершины 



Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим


Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула
[spoiler title=”источники:”]
http://mathforyou.net/online/vectors/volume/tetrahedron/
http://2mb.ru/matematika/geometriya/obem-tetraedra/
[/spoiler]
Объём треугольной пирамиды (тетраэдра)
равен (1/6) от величины
смешанного произведения векторов
на которых она построена:
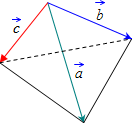
Так как значение смешанного произведения векторов может быть числом отрицательным, а объём тетраэдра – только положительным, то при вычислении объёма треугольной пирамиды (тетраэдра), построенной на векторах, результат смешанного произведения берется по модулю:
Вычислить объём треугольной пирамиды (тетраэдра), построенной на векторах поможет наш онлайн калькулятор с описанием хода решения на русском языке.