Онлайн калькулятор. Объем пирамиды (объем тетраэдра) построенной на векторах.
Этот онлайн калькулятор позволит вам очень просто найти объем пирамиды или объем тетраэдра построенных на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление объема пирамиды построенной на векторах и закрепить пройденый материал.
Калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Выберите каким образом задается пирамида (тетраэдр):
Введите значения векторов: Введите координаты вершин пирамиды:
Инструкция использования калькулятора для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
Ввод данных в калькулятор для вычисления объема пирамиды (объема тетраэдра) построенной на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления объема пирамиды (объема тетраэдра) построенной на векторах
- Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.
Теория. Объем пирамиды (объем тетраэдра) построенной на векторах

Определение Объем пирамиды (объем тетраэдра) построенной на векторах a , b и c равен шестой части модуля смешанного произведения векторов составляющих пирамиду:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Объем треугольной пирамиды (тетраэдра), построенной на векторах онлайн
Объём треугольной пирамиды (тетраэдра) равен (1/6) от величины смешанного произведения векторов на которых она построена:
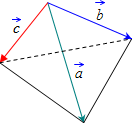
Так как значение смешанного произведения векторов может быть числом отрицательным, а объём тетраэдра – только положительным, то при вычислении объёма треугольной пирамиды (тетраэдра), построенной на векторах, результат смешанного произведения берется по модулю:
Вычислить объём треугольной пирамиды (тетраэдра), построенной на векторах поможет наш онлайн калькулятор с описанием хода решения на русском языке.
Объем тетраэдра
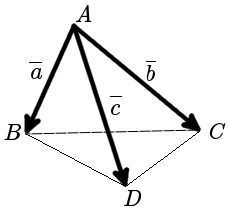
Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC .  Треугольники, из которых состоит тетраэдр, называются его гранями.
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра
Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.
 Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.
Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.
Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.
Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле
- S – площадь любой грани,
- H – высота, опущенная на эту грань
Правильный тетраэдр – частный вид тетраэдра
Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:
- Все грани равны.
- Все плоские углы правильного тетраэдра равны 60°
- Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
- Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).

Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна 
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой
 , где
, где
BM= , DM=
, DM= , BD=a,
, BD=a,
p=1/2 (BM+BD+DM)= 
Подставим эти значения в формулу высоты. Получим 
Вынесем 1/2a. Получим


Применим формулу разность квадратов

После небольших преобразований получим


Объем любого тетраэдра можно рассчитать по формуле  ,
,
где  ,
,

Подставив эти значения, получим 
Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра
Вычисление объема тетраэдра, если известны координаты его вершин
Пусть нам даны координаты вершин тетраэдра 
Из вершины  проведем векторы
проведем векторы  ,
,  ,
,  .
.
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим



Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула
[spoiler title=”источники:”]
http://mathforyou.net/online/vectors/volume/tetrahedron/
http://2mb.ru/matematika/geometriya/obem-tetraedra/
[/spoiler]
Объём треугольной пирамиды (тетраэдра)
равен (1/6) от величины
смешанного произведения векторов
на которых она построена:

Так как значение смешанного произведения векторов может быть числом отрицательным, а объём тетраэдра – только положительным, то при вычислении объёма треугольной пирамиды (тетраэдра), построенной на векторах, результат смешанного произведения берется по модулю:
Вычислить объём треугольной пирамиды (тетраэдра), построенной на векторах поможет наш онлайн калькулятор с описанием хода решения на русском языке.
Тетраэдр – простейшее многогранное тело, гранями и основанием которого являются треугольники.
Онлайн-калькулятор объема тетраэдра
Тетраэдр имеет четыре грани, каждая их которых образована тремя сторонами. Вершин у тетраэдра четыре, из каждой выходит по три ребра.
Данное тело разделяется на несколько видов. Ниже приведена их классификация.
- Равногранный тетраэдр — у него все грани являются одинаковыми треугольниками;
- Ортоцентрический тетраэдр — все высоты, проведенные из каждой вершины на противолежащую грань, являются одинаковыми по длине;
- Прямоугольный тетраэдр — ребра, исходящие из одной вершины, образуют друг с другом угол в 90 градусов;
- Каркасный;
- Соразмерный;
- Инцентрический.
Формулы объема тетраэдра
Объем данного тела можно найти несколькими способами. Разберем их более подробно.
Через смешанное произведение векторов
Если тетраэдр построен на трех векторах с координатами:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем этого тетраэдра это смешанное произведение этих векторов, то есть такой определитель:
V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Известны координаты четырех вершин октаэдра. A(1,4,9)A(1,4,9), B(8,7,3)B(8,7,3), C(1,2,3)C(1,2,3), D(7,12,1)D(7,12,1). Найдите его объем.
Решение
A(1,4,9)A(1,4,9)
B(8,7,3)B(8,7,3)
C(1,2,3)C(1,2,3)
D(7,12,1)D(7,12,1)
Первым шагом является определение координат векторов, на которых построено данное тело.
Для этого необходимо найти каждую координату вектора путем вычитания соответствующих координат двух точек. Например, координаты вектора AB→overrightarrow{AB}, то есть, вектора, направленного от точки AA к точке BB, это разности соответствующих координат точек BB и AA:
AB→=(8−1,7−4,3−9)=(7,3,−6)overrightarrow{AB}=(8-1, 7-4, 3-9)=(7, 3, -6)
Далее, аналогично:
AC→=(1−1,2−4,3−9)=(0,−2,−6)overrightarrow{AC}=(1-1, 2-4, 3-9)=(0, -2, -6)
AD→=(7−1,12−4,1−9)=(6,8,−8)overrightarrow{AD}=(7-1, 12-4, 1-9)=(6, 8, -8)
Теперь найдем смешанное произведение данных векторов, для этого составим определитель третьего порядка, при этом принимая, что AB→=a⃗overrightarrow{AB}=vec{a}, AC→=b⃗overrightarrow{AC}=vec{b}, AD→=c⃗overrightarrow{AD}=vec{c}.
∣axayazbxbybzcxcycz∣=∣73−60−2−668−8∣=7⋅(−2)⋅(−8)+3⋅(−6)⋅6+(−6)⋅0⋅8−(−6)⋅(−2)⋅6−7⋅(−6)⋅8−3⋅0⋅(−8)=112−108−0−72+336+0=268begin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}=
begin{vmatrix}
7 & 3 & -6 \
0 & -2 & -6 \
6 & 8 & -8 \
end{vmatrix}=7cdot(-2)cdot(-8) + 3cdot(-6)cdot6 + (-6)cdot0cdot8 – (-6)cdot(-2)cdot6 – 7cdot(-6)cdot8 – 3cdot0cdot(-8) = 112 – 108 – 0 – 72 + 336 + 0 = 268
То есть, объем тетраэдра равен:
V=16⋅∣axayazbxbybzcxcycz∣=16⋅∣73−60−2−668−8∣=16⋅268≈44.8 см3V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}=frac{1}{6}cdot
begin{vmatrix}
7 & 3 & -6 \
0 & -2 & -6 \
6 & 8 & -8 \
end{vmatrix}=frac{1}{6}cdot268approx44.8text{ см}^3
Ответ
44.8 см3.44.8text{ см}^3.
Формула объема равногранного тетраэдра по его стороне
Эта формула справедлива только для вычисления объема равногранного тетраэдра, то есть такого тетраэдра, у которого все грани являются одинаковыми правильными треугольниками.
V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}
aa — длина ребра тетраэдра.
Определить объем тетраэдра, если дана его сторона, равная 11 см11text{ см}.
Решение
a=11a=11
Подставляем aa в формулу для объема тетраэдра:
V=2⋅a312=2⋅11312≈156.8 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 11^3}{12}approx156.8text{ см}^3
Ответ
156.8 см3.156.8text{ см}^3.
На нашем сайте вы можете оформить выполнение контрольных работ на заказ онлайн!
Тест по теме «Объем тетраэдра»


Калькулятор онлайн.
Вычисление объема пирамиды (тетраэдра) построенной на векторах.
Этот калькулятор онлайн вычисляет объем пирамиды (тетраэдра) построенной на векторах. Пирамида (тетраэдр) задаётся координатами трех векторов исходящими из
одной вершины пирамиды.
Онлайн калькулятор для вычисления объема пирамиды (тетраэдра) построенной на векторах не просто даёт ответ задачи, он приводит подробное решение с
пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )
Наши игры, головоломки, эмуляторы:
Немного теории.
Определение и геометрический смысл смешанного произведения векторов
Определение
Смешанным произведением трех векторов ( vec{a}, ; vec{b}, ; vec{c} ) называется число, равное скалярному произведению
вектора ( vec{a} ) на векторное произведение векторов ( vec{b} ) и ( vec{c} ), т.е.
( vec{a} cdot ( vec{b} times vec{c} ) )
Следующая теорема выражает геометрический смысл смешанного произведения векторов.
Теорема
Смешанное произведение ( vec{a} cdot ( vec{b} times vec{c} ) ) равно объёму параллелепипеда, построенного на
векторах ( vec{a}, ; vec{b}, ; vec{c} ) взятому со знаком “+”, если тройка ( vec{a}, ; vec{b}, ; vec{c} )
– правая, со знаком “-“, если тройка ( vec{a}, ; vec{b}, ; vec{c} ) – левая. Если же
( vec{a}, ; vec{b}, ; vec{c} ) компланарны, то ( vec{a} cdot ( vec{b} times vec{c} ) = 0 ). Другими
словами:
$$ vec{a} cdot ( vec{b} times vec{c} ) = left{
begin{array}{r l}
v, & если ;; vec{a}, vec{b}, vec{c} ;; text{правая тройка} \
-v, & если ;;vec{a}, vec{b}, vec{c} ;; text{левая тройка} \
0, & если ;;vec{a}, vec{b}, vec{c} ;; компланарны
end{array} right. $$

Следствие
Из теоремы легко выводится следующее тождество:
( vec{a} cdot ( vec{b} times vec{c} ) = ( vec{a} times vec{b} ) cdot vec{c} )
т.е. знаки ( cdot ) и ( times ) в смешанном произведении векторов можно менять местами.
В силу этого тождества смешанные произведения ( vec{a} cdot ( vec{b} times vec{c} ) ) и
( ( vec{a} times vec{b} ) cdot vec{c} ) можно обозначать более простым символом ( vec{a} vec{b} vec{c} )
Выражение смешанного произведения через координаты векторов
Теорема
Если векторы ( vec{a}, ; vec{b}, ; vec{c} ) заданы своими координатами
( vec{a} left( a_x; a_y; a_z right), ; ) ( vec{b} left( b_x; b_y; b_z right), ; ) ( vec{c} left( c_x; c_y; c_z right) )
то смешанное произведение ( vec{a} vec{b} vec{c} ) вычисляется по формуле:
( vec{a} vec{b} vec{c} = a_x begin{vmatrix} b_y & b_z \ c_y & c_z end{vmatrix} +
a_y begin{vmatrix} b_z & b_x \ c_z & c_x end{vmatrix} +
a_z begin{vmatrix} b_x & b_y \ c_x & c_y end{vmatrix} )
или
( vec{a} vec{b} vec{c} = a_x( b_y c_z – c_y b_z) + a_y ( b_z c_x – c_z b_x) + a_z( b_x c_y – c_x b_y) )
11
Лекция№6
Рассмотрим
произведение векторов
![]() ,
,
![]()
и
![]() ,
,
составленное следующим образом:
![]() .
.
Здесь первые два вектора перемножаются
векторно, а их результат скалярно на
третий вектор. Такое произведение
называется векторно-скалярным, или
смешанным, произведением трех векторов.
Смешанное произведение представляет
собой некоторое число.
Выясним
геометрический смысл выражения
![]() .
.
Теорема.
Смешанное произведение трех векторов
равно объему параллелепипеда, построенного
на этих векторах, взятому со знаком
«плюс», если эти векторы образуют правую
тройку, и со знаком «минус», если они
образуют левую тройку.
Доказательство..Построим
параллелепипед, ребрами которого
являются векторы
![]() ,
,
![]() ,
,
![]()
и вектор
![]() .
.
Имеем:
![]() ,
,
![]() ,
,
где
![]()
– площадь параллелограмма, построенного
на векторах
![]()
и
![]() ,
,
![]()
для правой тройки векторов и
![]()
для левой, где
![]()
– высота параллелепипеда. Получаем:
![]() ,
,
т.е.
![]() ,
,
где
![]()
– объем параллелепипеда, образованного
векторами
![]() ,
,
![]()
и
![]() .
.
Свойства смешанного произведения
1.
Смешанное произведение не меняется при
циклической перестановке его
сомножителей, т.е.
![]() .
.
Действительно,
в этом случае не изменяется ни объем
параллелепипеда, ни ориентация его
ребер.
2.
Смешанное произведение не меняется при
перемене местами знаков векторного и
скалярного умножения, т.е.
![]() .
.
Действительно,
![]()
и
![]() .
.
Знак в правой части этих равенств берем
один и тот же, так как тройки векторов
![]() ,
,
![]() ,
,
![]()
и
![]() ,
,
![]() ,
,
![]()
– одной ориентации.
Следовательно,
![]() .
.
Это позволяет записывать смешанное
произведение векторов
![]()
в виде
![]()
без знаков векторного, скалярного
умножения.
3.
Смешанное произведение меняет знак при
перемене мест любых двух векторов-сомножителей,
т.е.
![]() ,
,
![]() ,
,
![]() .
.
Действительно,
такая перестановка равносильна
перестановке сомножителей в векторном
произведении, меняющей у произведения
знак.
4.
Смешанное произведение ненулевых
векторов
![]() ,
,
![]()
и
![]()
равно нулю тогда и только тогда, когда
они компланарны.
2.12. Вычисление смешанного произведения в координатной форме в ортонормированном базисе
Пусть
заданы векторы
![]() ,
,
![]() ,
,
![]() .
.
Найдем их смешанное произведение,
используя выражения в координатах для
векторного и скалярного произведений:

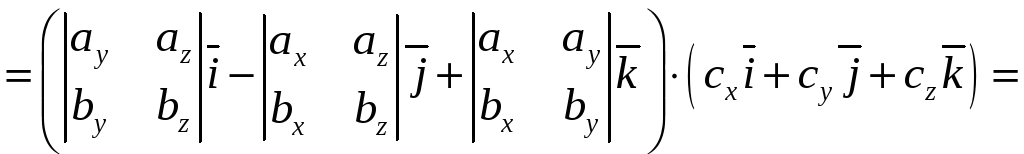
 . (10)
. (10)
Полученную
формулу можно записать короче:
 ,
,
так как правая часть
равенства (10) представляет собой
разложение определителя третьего
порядка по элементам третьей строки.
Итак,
смешанное произведение векторов равно
определителю третьего порядка,
составленному из координат перемножаемых
векторов.
2.13.Некоторые приложения смешанного произведения
Определение
взаимной ориентации векторов в
пространстве
Определение
взаимной ориентации векторов
![]() ,
,
![]()
и
![]()
основано на следующих соображениях.
Если
![]() ,
,
то
![]() ,
,
![]() ,
,
![]()
– правая тройка; если
![]() ,
,
то
![]() ,
,
![]() ,
,
![]()
– левая тройка.
Условие
компланарности векторов
Векторы
![]() ,
,
![]()
и
![]()
компланарны тогда и только тогда, когда
их смешанное произведение равно нулю
(![]() ,
,
![]() ,
,
![]() ):
):
 векторы
векторы
![]() ,
,
![]() ,
,
![]()
компланарны.
Определение
объемов параллелепипеда и треугольной
пирамиды
Нетрудно
показать, что объем параллелепипеда,
построенного на векторах
![]() ,
,
![]()
и
![]()
вычисляется как
![]() ,
,
а объем треугольной пирамиды, построенной
на этих же векторах, равен
![]() .
.
Пример
1. Доказать, что векторы
![]() ,
,
![]() ,
,
![]()
компланарны.
Решение.
Найдем смешанное произведение этих
векторов по формуле:
 .
.
. Это и означает,
что векторы
![]()
компланарны.
Пример 2.
Даны вершины тетраэдра:
![]()
(0, -2, 5),
![]()
(6, 6, 0),![]()
(3, -3, 6),
![]()
(2, -1, 3). Найти длину его высоты, опущенной
из вершины
![]() .
.
Решение.
Найдем сначала объем тетраэдра
![]() .
.
По формуле получаем:
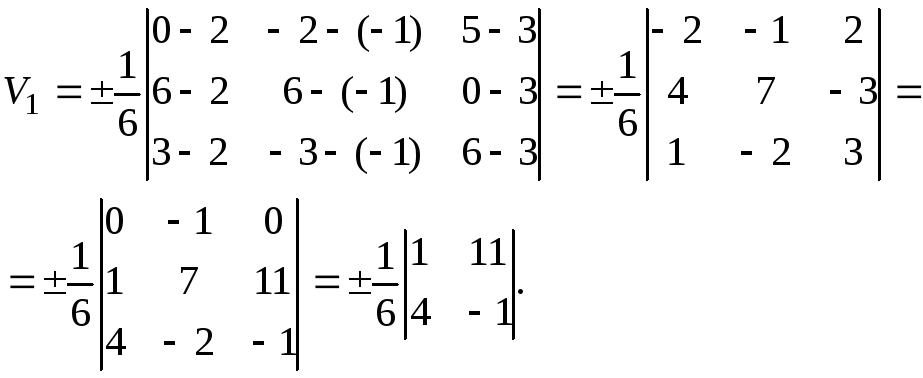
Так как
определитель равен отрицательному
числу, то в данном случае перед формулой
нужно взять знак минус. Следовательно,
![]() .
.
Искомую
величину h определим
из формулы
![]() ,
,
где S – площадь
основания. Определим площадь S:
![]()
где
![]()
![]()
Поскольку
![]()
![]()
то
![]()
Подставляя
в формулу
![]()
значения
![]()
и
![]() ,
,
получим h=3.
Пример 3.
Образуют ли векторы![]()
базис в пространстве ? Разложить вектор
![]()
по базису векторов
![]() .
.
Решение. Если векторы образуют
базис в пространстве, то они не лежат в
одной плоскости, т.е. являются
некомпланарными. Найдем смешанное
произведение векторов
![]() :
:
 ,
,
Следовательно,
векторы не компланарны и образуют базис
в пространстве. Если векторы образуют
базис в пространстве, то любой вектор![]()
можно представить в виде линейной
комбинации базисных векторов, а именно
![]() ,где
,где
![]()
координаты вектора
![]() в
в
базисе векторов
![]() .
.
Найдем эти координаты, составив и решив
систему уравнений
 .
.
Решая ее
методом Гаусса, имеем
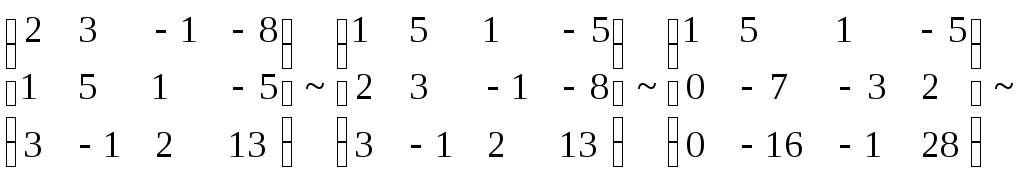







Отсюда
 .
.
Тогда
 .
.
Таким образом,
![]() .
.
Пример
4. Вершины пирамиды находятся в точках:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Вычислить:
а)
площадь грани
![]() ;
;
б) объем
пирамиды
![]() ;
;
в)
проекцию вектора
![]()
на направление вектора
![]() ;
;
г) угол
![]() ;
;
д)
проверить, что векторы
![]() ,
,
![]() ,
,
![]()
компланарны.
Решение
а) Из
определения векторного произведения
известно, что:
![]() .
.
Находим
векторы
![]()
и
![]() ,
,
используя формулу
![]() ;
;
![]() ,
,
![]() .
.
Для
векторов, заданных своими проекциями,
векторное произведение находится по
формуле
 ,
,
где
 .
.
Для
нашего случая
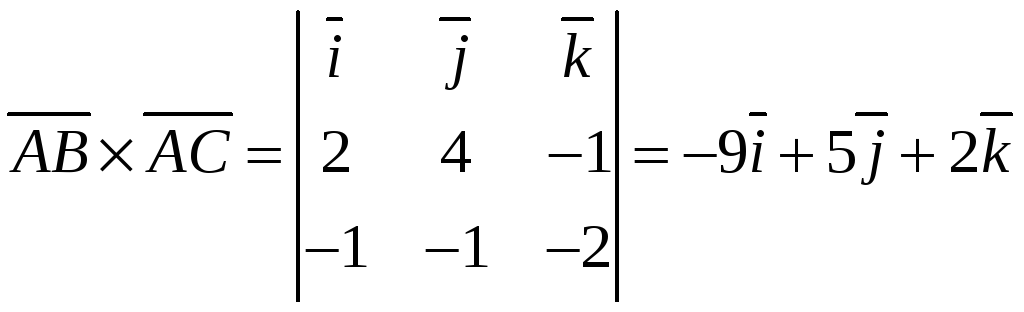 .
.
Длину
полученного вектора находим, используя
формулу
![]() ,
,
![]() .
.
![]()
и тогда
![]()
(кв. ед.).
б)
Смешанное произведение трех векторов
по абсолютной величине равно объему
параллелепипеда, построенного на
векторах
![]() ,
,
![]() ,
,
![]()
как на ребрах.
Смешанное
произведение вычисляется по формуле:
 .
.
Найдем
векторы
![]() ,
,
![]() ,
,
![]() ,
,
совпадающие с ребрами пирамиды,
сходящимися к вершине
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Смешанное
произведение этих векторов
 .
.
Так
как объем пирамиды равен
![]()
части объема параллелепипеда, построенного
на векторах
![]() ,
,
![]() ,
,
![]() ,
,
то
![]()
(куб. ед.).
в)
Используя формулу
![]() ,
,
определяющую скалярное произведение
векторов
![]() ,
,
![]() ,
,
можно записать так:
![]() ,
,
где
![]()
или
 ;
;
![]()
или
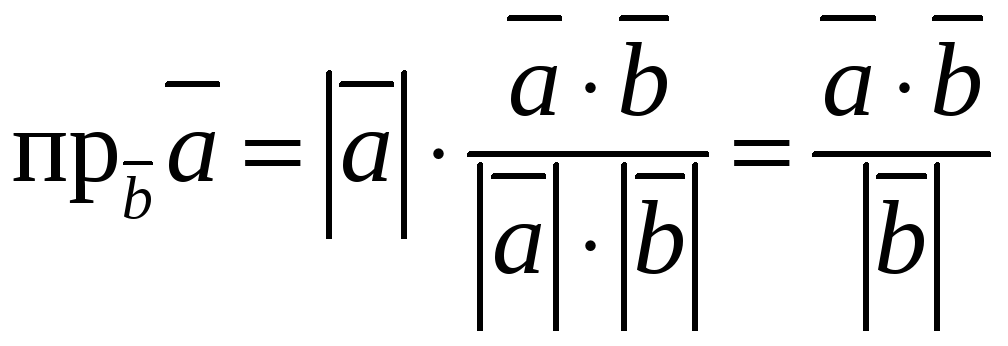 .
.
Для
нахождения проекции вектора
![]()
на направление вектора
![]()
находим координаты векторов
![]() ,
,
![]() ,
,
а затем, применяя формулу
 ,
,
получаем
 .
.
г) Для
нахождения угла
![]()
определяем векторы
![]() ,
,
![]() ,
,
имеющие общее начало в точке
![]() :
:
![]() ,
,
![]() .
.
Затем
по формуле скалярного произведения
![]()
находим
 ,
,
 .
.
д) Для
того чтобы три вектора
![]() ,
,
![]() ,
,
![]()
были компланарны,
необходимо и достаточно, чтобы их
смешанное произведение было равно нулю.
В нашем
случае имеем
 .
.
Следовательно,
векторы компланарны.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
