Калькулятор объема конуса
Рассчитайте онлайн объем для любых конусовидных объектов в кубических метрах или литрах.
Что известно
Размерность
Радиус основания
см
Диаметр основания
см
Площадь основания
см2
Высота
см
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🧮 Что такое калькулятор объема конуса?
Калькулятор объема конуса — это онлайн инструмент, который позволяет вычислить объем конуса при заданных значениях его радиуса основания и высоты.
Данный онлайн-калькулятор удобен для быстрого и точного расчета объема конуса без необходимости вручную применять формулу для расчета.
Какую формулу использует калькулятор?
Калькулятор объема конуса онлайн использует формулу для расчета объема правильного конуса, которая выглядит следующим образом:
V = 1/3 * π * r2 * h
где V – объем конуса, π – математическая константа (приблизительно равна 3,14159), r – радиус основания конуса, h – высота конуса.
В чем может быть полезен такой калькулятор?
Калькулятор объема конуса онлайн может быть полезен в различных областях, например:
- В учебной деятельности – калькулятор позволяет быстро и удобно вычислять объем конуса при решении задач в школе, вузе или других образовательных учреждениях.
- В профессиональной деятельности – инженеры, архитекторы, дизайнеры и другие специалисты могут использовать калькулятор для расчета объемов конических форм в проектах, таких как проектирование зданий, оборудования и т.д.
- В повседневной жизни – калькулятор может пригодиться при решении бытовых задач, например, при расчете объема цветочного горшка в форме конуса, объема мороженого в стаканчике или других предметов, имеющих форму конуса.
- В производстве – калькулятор может использоваться для расчета объема конических контейнеров, таких как силосы, резервуары, баки и т.д. Это может помочь определить необходимый объем материала, который нужно использовать при изготовлении таких контейнеров, и при планировании их транспортировки и хранения.
Также калькулятор объема конуса онлайн может быть полезен для тех, кто интересуется математикой и хочет изучить формулы и свойства конуса более подробно.
Какие преимущества имеет коническая форма?
Конусообразная форма имеет ряд преимуществ в различных областях:
- Прочность – из-за своей конической формы конструкции, такие как башни, мачты и башенные краны, имеют высокую прочность и устойчивость к ветру и другим нагрузкам.
- Эффективность – конические формы могут быть эффективными для передачи или направления потока жидкости, газа или другого материала, так как конусное сужение может ускорять поток, повышая его скорость.
- Удобство – конические формы могут быть удобными для хранения и транспортировки предметов, так как они занимают меньше места при хранении, чем другие формы.
- Эстетика – конические формы могут иметь эстетическую привлекательность и использоваться в дизайне зданий, мебели, украшений и т.д.
- Возможность распределения нагрузок – коническая форма может распределять нагрузки на более широкую область, что позволяет уменьшить напряжения и повысить прочность конструкций.
- Простота конструкции – конические формы могут быть проще в изготовлении и сборке, так как они имеют меньшее количество деталей и сложных соединений, чем другие формы.
❓Вопросы и ответы
Часто задаваемые вопросы и ответы по калькулятору объема конуса онлайн.
Что такое калькулятор объема конуса онлайн?
Калькулятор объема конуса онлайн — это инструмент, который позволяет рассчитать объем конуса на основе его радиуса и высоты.
Как использовать калькулятор объема конуса онлайн?
Для использования калькулятора нужно ввести значение радиуса и высоты конуса в соответствующие поля и нажать кнопку “Рассчитать”. Результат, т.е. объем конуса, будет показан ниже.
Можно ли использовать калькулятор для расчета объема усеченного конуса?
Нет, калькулятор объема конуса онлайн не предназначен для расчета объема усеченного конуса.
Можно ли использовать калькулятор объема конуса для расчета объема других трехмерных фигур?
Нет, калькулятор объема конуса онлайн предназначен только для расчета объема конуса. Для расчета объема других трехмерных фигур существуют другие калькуляторы.
Могу ли я использовать дробные значения для радиуса и высоты конуса?
Да, вы можете использовать дробные значения для радиуса и высоты конуса в калькуляторе объема конуса онлайн.
Для каких целей может быть полезен калькулятор объема конуса онлайн?
Калькулятор объема конуса онлайн может быть полезен для профессионалов, работающих в области строительства, дизайна и инженерии, а также для учеников и студентов, изучающих геометрию и математику.
Я не знаю, как найти радиус и высоту конуса. Что мне делать?
Радиус и высота конуса могут быть определены с помощью соответствующих измерений или данных. Если у вас нет этих данных, вы можете попробовать использовать другие методы расчета объема конуса, такие как измерение площади основания и умножение на высоту, но для этого вам нужно знать другие параметры конуса.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Поскольку объем конуса равен произведению высоты на треть площади основания конуса, то, зная объем и высоту, легко найти площадь круга в основании, а затем радиус и диаметр конуса.
S_(осн.)=3V/h
r=√(S_(осн.)/π)=√(3V/πh)
d=2r=2√(3V/πh)
Чтобы найти образующую конуса через объем и высоту, необходимо построить прямоугольный треугольник с образующей в виде гипотенузы и радиусом и высотой как катетами треугольника. Тогда образующая будет равна квадратному корню из суммы квадратов высоты и радиуса по теореме Пифагора, а угол между основанием и образующей можно будет найти через тангенс отношения высоты к радиусу. (рис.40.1)
l=√(h^2+r^2 )=√(h^2+3V/πh)
tanβ=h/r=h/√(3V/πh)=h√(πh/3V)
Угол раствора конуса можно найти, зная угол между образующей и основанием, и соединив их в равнобедренном треугольнике, где боковой стороной будет образующая, а основанием треугольника – диаметр конуса. (рис.40.2)
α=180°-2β
Площадь боковой поверхности конуса равна произведению радиуса на образующую и число π, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания, которую можно найти через объем.
S_(б.п.)=πrl=π√(3V/πh (h^2+3V/πh) )
S_(п.п.)=S_(б.п.)+S_(осн.)=π√(3V/πh (h^2+3V/πh) )+3V/h
Радиусы вписанной и описанной около конуса сфер можно найти из отношений, связывающих не только высоту конуса, которая известна, но и образующую, а также радиус основания конуса. (рис.40.3,40.4)
r_1=hr/(l+r)=(h√(3V/πh))/(√(h^2+3V/πh)+√(3V/πh))=(h√3V)/(√(πh^3+3V)+√3V)
R=(h^2+3V/πh)/2h
Нахождение объема конуса: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать объем прямого кругового конуса и разберем примеры решения задач.
Формула вычисления объема
1. Через площадь основания и высоту
Объем (V) конуса равняется одной третьей произведения его высоты на площадь основания:
2. Через радиус основания и высоту
Как мы знаем, основанием конуса является круг, площадь которого вычисляется по формуле: S = πR 2 .
Следовательно, формулу для вычисления объема конуса можно представить в виде:
Т.е. объем конуса равняется одной третьей произведения его высоты на число π и на радиус основания в квадрате.
Примечание: в расчетах значение числа π округляется до 3,14.
Формула для нахождения объема усеченного конуса представлена в отдельной публикации.
Примеры задач
Задание 1
Найдите объем конуса, если известна площадь его основания – 50,24 см 2 , а также, высота – 9 см.
Решение:
Применим первую формулу, подставив в нее заданные значения:
Задание 2
Высота конуса равна 7 см, а его радиус – 3 см. Найдите объем фигуры.
Решение:
Воспользовавшись второй, более расширенной, формулой получаем:
Калькулятор для расчета объема конуса
C помощью нашего Онлайн-калькулятора для расчета объема конуса Вы можете быстро и точно рассчитать объем конуса. Для того, чтобы вычислить объем конуса, сначала выберите формулу, по которой Вы собираетесь произвести расчет. Объем конуса (в зависимости от исходных данных) можно вычислить двумя способами: 1. через высоту и радиус основания; 2. через высоту и площадь основания. Затем введите значения исходных данных для расчета (значение высоты конуса, значение радиуса основания конуса (или значение площади основания конуса) и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем конуса.
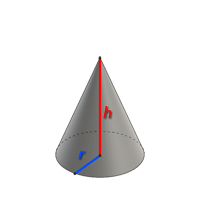
Конус – это геометрическое тело, которое образуется при вращение прямоугольного треугольника вокруг одного из его катетов. Такой конус также еще называется – прямой круговой конус.
Объем конуса можно вычислить по двум формулам:
- через высоту конуса и радиус основания;
- через высоту конуса и площадь основания.
Формула для определения объема конуса. Пример решения задачи
Каждый школьник при изучении стереометрии в старших классах сталкивался с конусом. Двумя важными характеристиками этой пространственной фигуры являются площадь поверхности и объем. В данной статье покажем, как находить объем круглого конуса.
Круглый конус как фигура вращения прямоугольного треугольника
Прежде чем переходить непосредственно к теме статьи, следует описать конус с геометрической точки зрения.
Пусть имеется некоторый прямоугольный треугольник. Если его вращать вокруг любого из катетов, то результатом этого действия станет искомая фигура, изображенная ниже на рисунке.
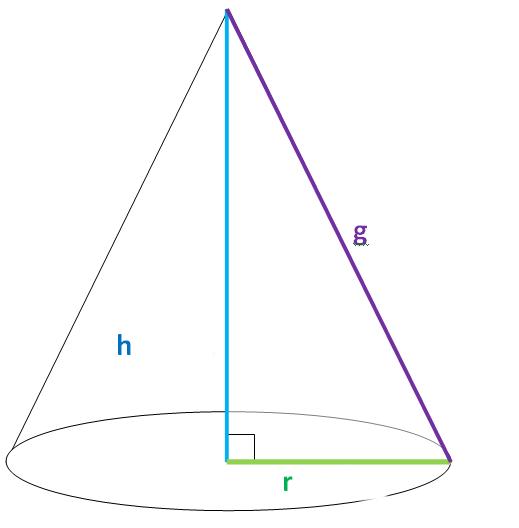
Здесь катет AB является частью оси конуса, а его длина соответствует высоте фигуры. Второй катет (отрезок CA) будет радиусом конуса. Во время вращения он опишет окружность, ограничивающую основание фигуры. Гипотенуза BC называется образующей фигуры, или ее генератрисой. Точка B – это вершина конуса, которая у него является единственной.
Учитывая свойства треугольника ABC, можно записать связь между генератрисой g, радиусом r и высотой h в виде следующего равенства:
Эта формула оказывается полезной при решении многих геометрических задач с рассматриваемой фигурой.
Формула объема конуса
Объемом всякой пространственной фигуры называют область пространства, которую ограничивают поверхности этой фигуры. Для конуса таких поверхностей две:
- Боковая, или коническая. Она образована всеми генератрисами.
- Основание. В данном случае оно является кругом.
Получим формулу для определения объема конуса. Для этого разрежем его мысленно на множество параллельных основанию слоев. Каждый из слоев имеет толщину dx, которая стремится к нулю. Площадь Sx слоя, который находится на расстоянии x от вершины фигуры, равна следующему выражению:
Справедливость этого выражения можно проверить интуитивно, если подставить значения x = 0 и x = h. В первом случае мы получим равную нулю площадь, во втором случае она будет равна площади круглого основания.
Для определения объема конуса необходимо сложит маленькие “объемчики” каждого слоя, то есть следует воспользоваться интегральным исчислением:
Вычисляя этот интеграл, приходим к конечной формуле для круглого конуса:
Любопытно отметить, что эта формула полностью аналогична той, которая используется для вычисления объема произвольной пирамиды. Это совпадение не случайное, ведь любая пирамида переходит в конус при увеличении количества ее ребер до бесконечности.
Задача на вычисление объема
Полезно привести пример решения задачи, который продемонстрирует использование выведенной формулы для объема V.
Дан круглый конус, у которого площадь основания равна 37 см 2 , а генератриса фигуры больше в три раза радиуса. Чему равен объем конуса?
Формулой для объема мы вправе воспользоваться, если знаем две величины: высоту h и радиус r. Найдем формулы, которые их определяют в соответствии с условием задачи.
Радиус r можно рассчитать, зная площадь круга So, имеем:
Пользуясь условием задачи, запишем равенство для генератрисы g:
Зная формулы для r и g, рассчитаем высоту h:
Мы нашли все необходимые параметры. Теперь пришло время подставить их в формулу для V:
Осталось подставить площадь основания So и вычислить значение объема: V = 119,75 см 3 .
[spoiler title=”источники:”]
http://calc.by/math-calculators/calculator-volume-cone.html
http://fb.ru/article/51455/cu-formula-dlya-opredeleniya-obyema-konusa-primer-resheniya-zadachi
[/spoiler]
Как рассчитать объем конуса
На данной странице калькулятор поможет рассчитать объем конуса онлайн. Для расчета задайте высоту, радиус или площадь. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Конус – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.
Через высоту и радиус
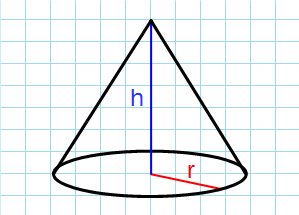
Формула объема конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Через высоту и площадь основания
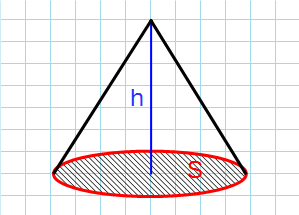
Формула объема конуса через высоту и площадь основания:
h – высота конуса; S – площадь основания.
Конус – это тело в пространстве, образованное путем вращения прямоугольного треугольника вокруг одного из его катетов.
Онлайн-калькулятор объема конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной.
Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
Формула объема прямого конуса
Объем прямого конуса можно рассчитать по следующей формуле:
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
где SоснS_{text{осн}} – площадь основания конуса;
hh – высота конуса.
Рассмотрим несколько примеров.
Найдите объем конуса, если его образующая ll равна 5см5text {см}, а радиус основания RR, которым является круг, равен 3 см3text{ см}.
Решение
l=5l=5
R=3R=3
Сперва найдем высоту конуса hh. Включим его в прямоугольный треугольник, гипотенузой которого является образующая. По теореме Пифагора:
l2=h2+R2l^2=h^2+R^2
Отсюда, hh:
h=l2−R2h=sqrt{l^2-R^2}
h=52−32h=sqrt{5^2-3^2}
h=25−9h=sqrt{25-9}
h=16h=sqrt{16}
h=4h=4
Затем находим площадь основания конуса. Это площадь круга радиуса RR:
Sосн=π⋅R2=π⋅32≈28.26S_{text{осн}}=picdot R^2=picdot3^2approx28.26
Последние вычисления — нахождение объема конуса по формуле:
V=13⋅Sосн⋅h≈13⋅28.26⋅4≈37.68 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 28.26cdot 4approx37.68text{ см}^3
Ответ: 37.68 см3.37.68text{ см}^3.
Известен диаметр круга DD лежащего в основании конуса, равен он 8 см8text{ см}. Высота конуса равна 9 см9text{ см}. Найдите его объем.
Решение
D=8D=8
h=9h=9
Найдем радиус RR круга через его диаметр:
R=12⋅D=82=4R=frac{1}{2}cdot D=frac{8}{2}=4
Площадь этого круга и есть основание нашего конуса:
Sосн=π⋅R2=π⋅42≈50.24S_{text{осн}}=picdot R^2=picdot4^2approx50.24
Сам объем равен:
V=13⋅Sосн⋅h≈13⋅50.24⋅9≈150.72 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 50.24cdot 9approx150.72text{ см}^3
Ответ: 150.72 см3.150.72text{ см}^3.
Вам нужно решить задачу по алгебре? Наши эксперты помогут вам!