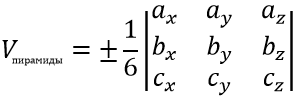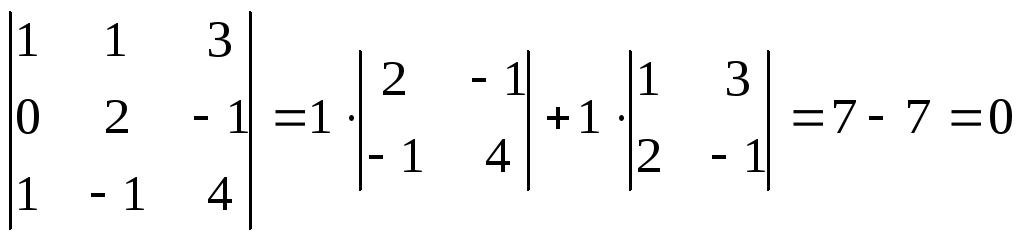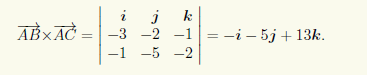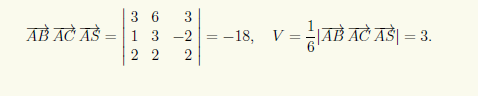Как найти объем треугольной пирамиды по векторам

Skip to content

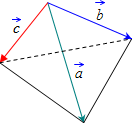
Объём треугольной пирамиды, построенной на векторах

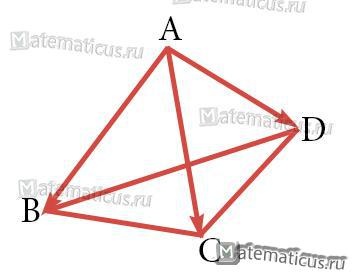
Рисунок — Треугольная пирамида, построенная на векторах

Объём треугольной пирамиды (см. рисунок выше), построенной на векторах вычисляется по формуле:

Пример

Найти объём треугольной пирамиды, построенной на векторах ABCD c вершинами

А(2; -1; 1), B(5;5;4), C(3;2;-1), D(4;1;3).

Решение

Находим координаты векторов

$overrightarrow {AB}  = left{ {left( {5 — 2} right);left( {5 — left( { — 1} right)} right);left( {4 — 1} right)} right} = left{ {3;6;3} right}$

$overrightarrow {AC}  = left{ {left( {3 — 2} right);left( {2 — left( { — 1} right)} right);left( { — 1 — 1} right)} right} = left{ {1;3; — 2} right}$

$overrightarrow {AD}  = left{ {left( {4 — 2} right);left( {1 — left( { — 1} right)} right);left( {2 — 1} right)} right} = left{ {2;2;2} right}$

Искомый объём равен $frac{1}{6}$ объём параллелепипеда, построенного на рёбрах,

$overrightarrow {AB} $, $overrightarrow {AС} $, $overrightarrow {AD} $, следовательно объем равен:

$V =  pm frac{1}{6}left| {begin{array}{*{20}{c}}3&6&3 \ 1&3&{ — 2} \ 2&2&2 end{array}} right|=$

$ =  pm frac{1}{6}cdotleft( {3cdotleft( {3cdot2 — left( { — 2} right)cdot2} right) — 6cdotleft( {1cdot2 — left( { — 2} right)cdot2} right) + 3cdotleft( {1cdot2 — 3cdot2} right)} right) = 3$

Решая, находим определитель матрицы третьего порядка и получаем искомый объём треугольной пирамиды V=3

17667

Объём треугольной пирамиды (тетраэдра)
равен (1/6) от величины
смешанного произведения векторов
на которых она построена:

Так как значение смешанного произведения векторов может быть числом отрицательным, а объём тетраэдра – только положительным, то при вычислении объёма треугольной пирамиды (тетраэдра), построенной на векторах, результат смешанного произведения берется по модулю:

Вычислить объём треугольной пирамиды (тетраэдра), построенной на векторах поможет наш онлайн калькулятор с описанием хода решения на русском языке.

Уставление
компланарности векторов в пространстве

Пример
12: Доказать
компланарность векторов
=
1
1; 3 ,

= 0

2 -
1 ,

= 1
– 1
4 .

Решение.
Найдем смешанное произведение векторов

:

=

(определитель
вычислен путем его разложения по
элементам первого столбца).

Так
как смешанное произведение векторов
,

и

равно нулю, то эти векторы компланарны.

Определение объемов параллелепипеда и треугольной пирамиды

Пример
13:Найти объём
треугольной пирамиды с вершинами в
точках

Решение.
Найдем
координаты векторов
,,,
на которых построена пирамида:

Вычислим
смешанное произведение этих векторов

Объём
треугольной пирамиды, построенной на
векторах
,,,
равен

Определение взаимной ориентации векторов

Определение
взаимной ориентации векторов
,,
_{основано
на следующих соображениях. Если
>0,
то тройка векторов правая, если
<
0, то тройка векторов левая.}

2. Задачи для самостоятельной работы

1.
По данным векторам а
и b
построить следующие их линейные
комбинации: а) 2а
+ b;
б) а
— Зb;
в) — а
+ 4-b;

2.
Векторы
служат сторонами треугольника ABC.
Выразить через а,
b,
с
векторы

совпадающие с медианами треугольника.

3.
В треугольной пирамиде SABC известны
векторы Найти вектор
,
если точка О является центром масс

треугольника
ABC.

4.
Дана прямоугольная трапеция ABCD, длины
оснований AD н ВС которой соответственно
равны 4 и 2, а угол D равен 45°. Найти проекции
векторов
на
ось

определяемую вектором
.

5.
Вектор а
составляет с координатными осямн Ох и
Оу углы
.
Вычислить его координаты, если |а|
=2.

6.
Найти длины диагоналей параллелограмма,
построенного на векторах

7.
Векторы
определяют
стороны треугольника ABC. Найти длину
вектора
,
совпадающего с медианой, проведенной
из вершины С.

8.В
параллелограмме ABCD
даны стороны

Выразить
через
ивекторы

9.
В ТреугольникеABCпроведины меридианыaAK,BLиCM.
Выразить
и
через векторыи.

10.
Даны векторыи.
Найти векторы:
;.

11.
Найти направляющие
косинусы вектора

12.Дано
=5,=6.
Найти скалярное произведение векторови,
если уголмежду ними равен 120°

13.
Найти угол А в треугольнике с вершинами
A(1;2;-1),B(5;5;11),C(13;18;20)

14.
Даны векторы
,,.
Найти проекцию векторана вектор.

15.
Даны векторы
,и.
Найти проекцию векторана вектор.

16.
Найти
,
если

17.
Даны векторы
и.
При каком значенииm
эти векторы перпендикулярны?

18.Даны
три последовательные вершины
параллелограмма А (-3;-2;0), В(3;-3;1) и С(5;0;2).
Найти четвёртую вершину D
и угол между векторами
и.

19.
Даны векторы
и.
При каком значенииm
векторы перпендикулярны?

20.
Найти площадь треугольника с вершинами
А (2;2;2), В(1;3;3), С(3;4;2).

21.
Упростить:

22.
Известно, что
а
угол между
иравен
Найти
.

23.
Найти площадь треугольника с вершинами
в точках

24.
Вычислить площадь треугольника с
вершинами А (1;1;1), В (2;3;4), С (4;3;2).

25.
Вычислить площадь и высоту параллелограмма,
построенного на векторах

26.
Найти площадь параллелограмма,
построенного на векторах
и,
где.

27.
Вычислить диагонали и площадь
параллелограмма, построенного на
векторах
и.

28.
Найти значения α и β, при которых векторы
=и=являются коллинеарными.

29.
На оси аппликат найти точку, равноудаленную
от точек А(3;9;-1) и В(7;-3;9)

30.
Определите координаты концов P
и Q
отрезка, который точками М(3;1;3) и N(6;-1;1)
разделён на три части.

31.
Проверить, является ли векторы
компланарными?

32.
Найти объём тетраэдра с вершинами в
точках А (-1;1;0), В(2;-2;1), С(3;1;-1), D(1;0;-2).

33.
Вычислить объём параллелепипеда,
построенного на векторах
и.

34.
Установить, лежат ли в одной плоскости
точки А (4;3;10), В (5;1;5), С (2;2;5), D
(3;4;12).

35.
В тетраэдре с вершинами D
(-3;-3;-3), A
(2;-1;-3), B
(-1;2;3) и

C(-2;-2;1).
Найти площадь грани АВС и длину высоты,
проведённой к этой грани.

36.Выяснить,
компланарны ли векторы
?

34.
Определить
,
при котором компланарны векторы
и

37.
Найти объем тетраэдра с вершинами в
точках А (-1; 1; 0 ), В ( 2; -2; 1 ), С (3; 1; -1 ),
D
=(1; 0; -2 ).

38.
На прямой проходящей через точки А
(-3;8;2) и B
(1;-2;0) найти точку С, абсцисса которой

39.
Найти объём треугольной пирамиды с
вершинами в точках

40.
Найти точку пересечения медиан
треугольника, если вершинами его служат
точки А(7;-4;5), В(-1;8;-2), С(-12;-1;6).

41.
Найти все значения m, при
которых вектора (1;m;
3) линейно выражается через векторыb(2;3;7),c(3;-2;4),d(-1;1;-1).

42.
Предприятие выпускает 4 вида продукции
Р₁, Р₂;
Р_3,
Р₄
в количествах 50, 80, 20,120 единиц. При этом
нормы расхода сырья составляют
соответственно 7; 3,5; 10; 4 кг. Определите
суммарный расход сырья и его изменение
при изменениях выпуска продукции Р₁,
Р₂; Р_3,
Р₄ соответственно
+5, -4, -2, +10 единиц.

43.
Предприятие выпускает три вида продукции
Р₁, Р₂;
Р₃
в количестве 15, 25, 40 штук, реализуемых
по ценам 30, 40, 50 усл. Ед. соответственно.
Найти выручку предприятия от реализации
продукции и ее изменение при изменении
Р₁, Р₂;
Р₃цен
продукции соответственно на +5, -3, +2 усл.
ед.

44.
Выяснить, являются ли векторы а₁=(4;-5;2;6),
а₂=(2;-2;1;3),
а₃=(6;-3;3;9),
а₄=(4;
-1;5;6) линейно зависимыми?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Коллинеарные векторы

Коллинеарными называются векторы, лежащие на параллельных прямых (или на одной и той же прямой).

Коллинеарные векторы могут иметь одно и то же направление (равнонаправленные векторы) или противоположные направления.

Два ненулевых вектора равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы считаются равными.

Условие коллинеарности векторов

Если векторы a(x₁,y₁,z₁) и b(x₂,y₂,z₂) коллинеарны, то их соответствующие координаты пропорциональны:

x₂/x₁ = y₂/y₁ = z₂/z₁ 

И обратно: если соответствующие координаты векторов пропорциональны, то векторы эти — коллинеарны.

Если коэффициент пропорциональности λ = x₂/x₁ = y₂/y₁ = z₂/z₁ положителен, то векторы a и b равнонаправлены, а если отрицателен — то противоположно направлены.

Например:

• векторы АВ(3, 5, 8) и CD(6, 10, 16) коллинеарны;
• векторы АВ(-12, -8, -22) и CD(6, 4, 11) коллинеарны;
• векторы АВ(-10, -8, -21) и CD(6, 5, 11) не коллинеарны

Компланарные векторы

Три вектора (или большее их число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.

Если хотя бы один из трёх векторов — нулевой, то три вектора также считаются компланарными.

Компланарность векторов, доказательство их компланарности

Необходимым и достаточным условием компланарности трёх векторов a, b, c является равенство нулю их смешанного произведения.

Например:

• векторы AB(2, 1, 3), CD(-2, 8, 12), EF(3, 15, 27) компланарны;
• векторы AB(-4, 2, -6), CD(-1, -4, 6), EF(-2, 10, -18) компланарны.

Смешанное произведение векторов

Смешанным (или векторно-скалярным) произведением трёх векторов a, b, c называется скалярное произведение вектора а на векторное произведение b×c, т.е. число а(b×c), или, что то же, (b×c)а.

Для того, чтобы найти смешанное произведение трёх векторов a, b и c, заданных своими координатами a(a_x,a_y,a_z), b(b_x,b_y,b_z), c(c_x,c_y,c_z), нужно определенным образом составить определитель третьего порядка. В первой строке определителя записываем координаты первого вектора, во второй строке — второго, в третьей — третьего:

a_x         a_y         a_z

b_x         b_y         b_z

c_x         c_y         c_z

и вычисляем определитель. Результат вычислений и есть искомое смешанное произведение трёх векторов.

Например, смешанное произведение векторов a(-2, 5, -3), b(1, -4, 6), c(1, 5, 9) равно 90.

Смешанное произведение abc трех некомпланарных векторов a, b, c равно объёму параллелепипеда, построенного на векторах a, b, c, взятому со знаком «плюс», если система a, b, c — правая, и со знаком «минус», если эта система левая.

Иногда вопрос задают так: «Чему равен объём параллелепипеда, построенного на векторах a, b и c?». Как уже известно, равен он смешанному произведению векторов a, b и c. Если результат окажется со знаком «минус», то результат, конечно же, нужно взять по модулю.

Например, объём параллелепипеда, построенного на векторах a(-2, 5, -3), b(1, -4, 6), c(1, 5, 9), равен 90 кубических единиц.

Объём пирамиды, построенной на векторах

Объём пирамиды, построенной на векторах a, b и c, равен 1/6 объёма параллелепипеда, построенного на векторах a, b и c.

Если известны координаты вершин A, B, C, D пирамиды, то последовательность действий для нахождения её объёма следующая:

• находим координаты векторов AB, AC и AD;
• находим 1/6 смешанного произведения векторов AB, AC и AD (результат вычислений берём со знаком «плюс»).

Например, даны вершины пирамиды ABCD:

• A(5, 0, 14);
• B(-7, 16, 9);
• C(14, -5, 17);
• D(15, 11, -2).

Находим координаты векторов AB, AC и AD:

• AB = (-7-5, 16-0, 9-14) = (-12, 16, -5);
• AC = (14-5, -5-0, 17-14) = (9, -5, 3);
• AD = (15-5, 11-0, -2-14) = (10, 11, -16).

Вычисляем 1/6 смешанного произведения векторов AB, AC и AD.

V = 1/6 · 1475 = 245,83 кубических единиц.

Источники:

• М.Я. Выгодский. Справочник по высшей математике.
• В.Д. Черненко. Высшая математика в примерах и задачах. В 3 томах. Том 1.

Дополнительно на Геноне:

• Что такое определитель матрицы?
• Как найти определитель матрицы?
• Какими свойствами обладает определитель матрицы?

Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.

Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.

Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3; —1;2).

Для определения площади ΔABC с помощью (4.10) найдем координаты векторов AB и AC: AB = {1 — 4; 2 — 4; 3 — 4} = { — 3; —2; —1}, —1 = {3 — 4; —1 — 4; 2 — 4} = { — 1; —5; —2}.

Затем по (3.2) вычислим их векторное произведение:

Модуль этого векторного произведения равен |AB×AC| = √((—1)² + (—5)² + 13²) = √195, и следовательно, S ΔABC = |AB×AC|/2 = √195/2 #

Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах AB, AC и AS. Таким образом, объем этой пирамиды равен VSABC = |ABACAS|/6.

Пример 4.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: A(2; —1;1), B(5; 5; 4), C(3; 2; —1), S(4;1;3).

Используя (4.10), вычисляем координаты векторов, направленных по ребрам пирамиды: AB = {5 — 2; 5 — (—1);4 — 1} = {3; 6; 3}, AC = {3 — 2; 2 — (—1); —1 — 1} = {1;3; —2},= AS {4 — 2;1 — (—1); 3 — 1} = {2;2;2}, и определяем объем с помощью смешанного произведения найденных векторов: