Объем призмы
Для нахождения объема призмы применяется общая универсальная формула:
V = Sh
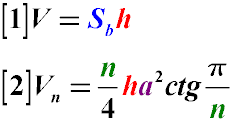
где:
V – объем призмы
Vn – объем призмы, в основании которой лежит правильный многоугольник с n сторонами
Sb – площадь основания призмы
h – высота призмы
n – количество сторон правильного многоугольника, который лежит в основании призмы
a – длина стороны правильного многоугольника
Как найти объем треугольной призмы (с треугольником в основании)
Если в основании призмы лежит треугольник, то для нахождения ее объема можно применить формулы нахождения площади треугольника и умножить полученное значение на высоту призмы.
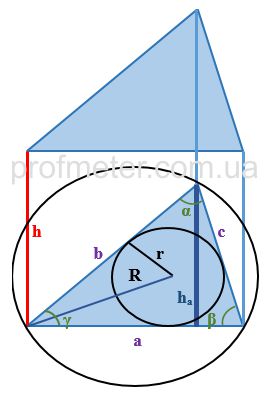
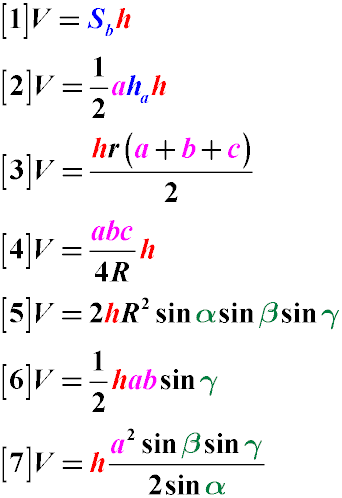
Объем треугольной призмы можно найти через высоту основания ha и сторону a, на которую эта высота опущена (Формула 2). Не путайте ha и h.
Объем треугольной призмы можно найти через радиус вписанной окружности r и сумму длин сторон основания (a,b,c).(Формула 3)
Объем треугольной призмы можно вычислить как произведение длин сторон основания на четыре радиуса описанной окружности R, умноженное на высоту призмы. (Формула 4)
Также, зная радиус описанной окружности, объем треугольной призмы можно найти как произведение синусов всех углов основания на квадрат радиуса описанной окружности, умноженное на удвоенную высоту призмы (Формула 5).
Если известен угол между двумя сторонами основания и сами эти стороны, то половина произведения сторон основания на синус угла между ними и на высоту призмы, также позволит вычислить ее объем (Формула 6).
Есть также формулы нахождения объема призмы для специальных случаев, когда в основании лежит геометрическая фигура с “особенностями”. Например, если в основании прямой призмы лежит равносторонний, прямоугольный или равнобедренный треугольник, тогда количество формул, которыми можно воспользоваться для расчета объем призмы, существенно расширяется:
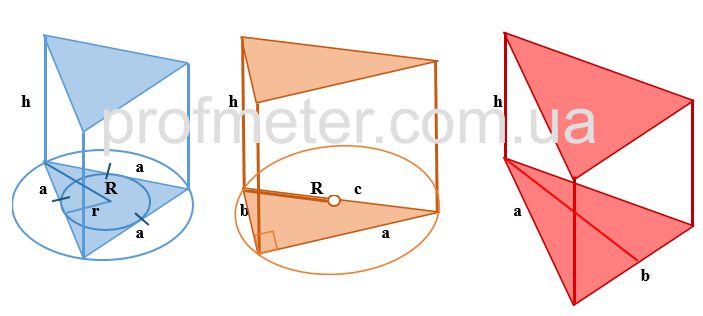
Объем правильной треугольной призмы (с правильным треугольником в основании)
На рисунке выше правильная треугольная призма изображена синим цветом.
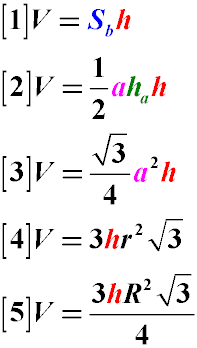
Где:
V – объем правильной треугольной призмы
ha – высота основания, опущенная на сторону основания a
h – высота призмы
r – радиус вписанной в основание окружности
R – радиус окружности, описанной вокруг основания правильной треугольной призмы
Объем призмы с прямоугольным треугольником в основании
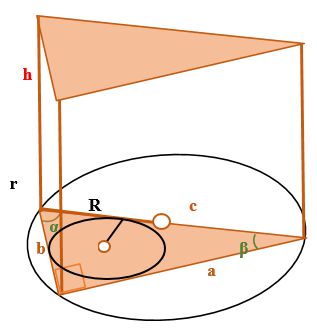
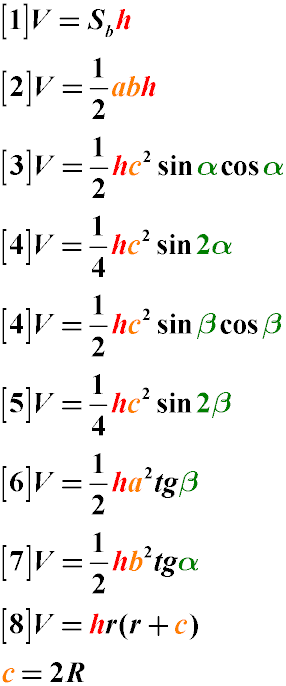
Где:
V – объем призмы с прямоугольным треугольником в основании
h – высота призмы
α – угол основания, противолежащий стороне a (катету a) прямоугольного треугольника
β – угол основания, противолежащий стороне b (катету b) прямоугольного треугольника
a,b – катеты прямоугольного треугольника, который является основанием призмы
c – гипотенуза прямоугольного треугольника, который является основанием призмы
r – радиус вписанной в основание призмы окружности
R – радиус описанной вокруг основания призмы, которое является прямоугольным треугольником, окружности
Учтите, что если, вокруг прямоугольного треугольника описана окружность, то гипотенуза треугольника лежит на ее диаметре, то есть c = 2R. Поэтому, при необходимости, можно заменить в формулах c на (2R).
Объем призмы с равнобедренным треугольником в основании
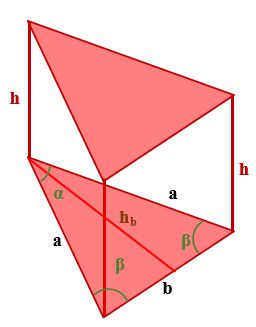
Если в основании призмы лежит равнобедренный треугольник, для нахождения ее объема можно воспользоваться следующими формулами:
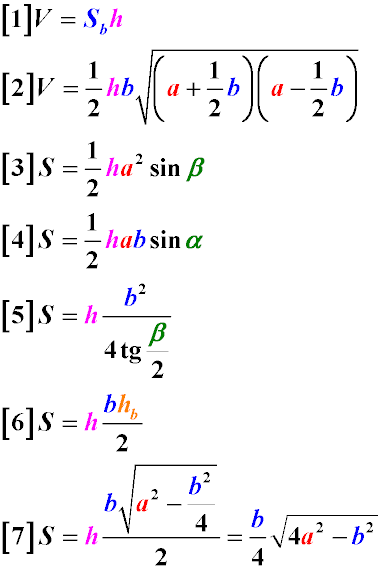
где:
V– объем призмы с равнобедренным треугольником в основании
h – высота призмы
hb – высота равнобедренного треугольника, опущенная на его основание
a – длина одной из равных сторон равнобедренного треугольника, лежащего в основании призмы
b – основание равнобедренного треугольника
α – угол между сторонами и основанием равнобедренного треугольника
β – угол между равными сторонами равнобедренного треугольника, который лежит в основании призмы
Объем параллелепипеда и куба
Если в основании прямой призмы лежит прямоугольник, то количество формул для нахождения объема такой призмы также будет больше:
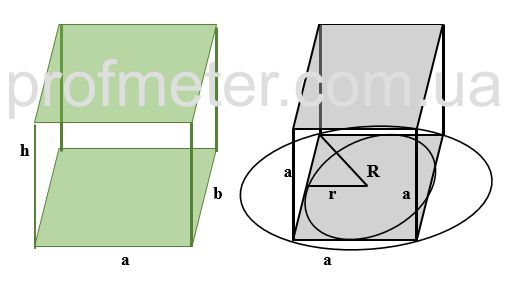
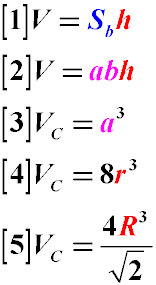
где:
V – объем призмы, в основании которой лежит прямоугольник
Vc – объем куба
h – высота призмы
a – длина стороны основания
b – длина второй стороны основания
R – радиус окружности, описанной вокруг основания куба
r – радиус окружности, вписанной в основание куба
0
Призма. Параллелепипед. Куб. Решение задач |
Описание курса
| Площадь боковой поверхности призмы
Объем призмы
Объем призмы ранен V = Sоснов • H. где Sоснов — площадь основания призмы. H — ее высота.
Исходим из известного факта: объем параллелепипеда, равен
Vпар = Sоснов • H
(Sоснов – площадь основания, H — высота).
Начнем с частного случая. Пусть нам дана треугольная призма.
Достроим ее до параллелепипеда. Следовательно, параллелепипед состоит из двух равных призм, поэтому
С другой стороны,
а высота призмы и параллелепипеда общая. Из равенства
следует, что
Переходим теперь к общему случаю. Дана произвольная призма. В ее основании лежит многоугольник. Проведя в нем диагонали, исходящие, из одной вершины, разбиваем многоугольник на треугольники (рис. 39). Сечения, проведенные через эти диагонали и соответствующие боковые ребра призмы делят ее на определенное число n треугольных призм. Для призмы с номером k объем равен
Vk = Sk • H
где Sk — площадь ее основания, H — высота первоначальной призмы. Складывая объем треугольных призм, получаем объем первоначальной призмы:
Формула установлена.
Тема. «Объёмы многогранников».
Методическое пособие по решению задач для студентов 2 курса СПО.
Дистанционная форма обучения.
1. Теоретический материал.
|
Вид многогранника |
Формула объёма |
|
1. Призма |
V=Sосн H |
|
2. Прямоугольный параллелепипед |
V=abc |
|
3. Куб |
V=a3 |
|
4. Пирамида |
V= |
|
5.Усеченная пирамида |
V= |
2. Решение задач.
Задача № 1
Найдите объем прямой призмы, в основании которой лежит ромб с диагоналями, равными 25 и 60, и боковым ребром, равным 25.
|
|
Дано: АВСДА1В1С1Д1 – прямая четырехугольная призма АС = 60; ВД = 25; АА1 = 25 Найти: V призмы Решение V призмы = Sосн H; Н=АА1 АВСД – ромб, следовательно Sосн = Sосн = Ответ. 18750 |
Задача № 2
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 8 и 15, боковое ребро равно 9. Найдите объем призмы.
|
|
Дано: АВСА1В1С1 – прямая треугольная призма.
АС = 15; ВС = 8; АА1 = 9 Найти: V призмы V призмы = Sосн H; Н=АА1
следовательно Sосн = Sосн = Ответ. 540 |
Задача № 3.
В основании наклонной треугольной призмы лежит треугольник со сторонами 14; 12 и 12. Боковое ребро равно 6 и наклонено к плоскость основания под углом 30 . Найти объём призмы.
. Найти объём призмы.
|
|
Дано: АВСА1В1С1 – наклонная треугольная призма. АС = 12; ВС = 12; АВ = 14; СС1 = 6; Найти: V призмы V призмы = Sосн H;
С1О С1О = С1С Н=ОС1 = 3 Sосн = р = Sосн = V призмы = Ответ. 21 |
Задача № 4.
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
|
|
Дано: прямоугольный параллелепипед; а=4; в=6; с=9. Vп.п = Vк Найти : d Решение: Vп.п =авс; Vп.п = 4 Vк = d3; d3 = 216; d = Ответ. 6 |
Задача № 5
От треугольной пирамиды, объем которой равен 34, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
|
|
Дано: VSАВС = 34; MN – средняя линия треугольника АВС Найти: VSMNC Решение: Так как MN – средняя линия треугольника АВС, то MN = Коэффициент подобия к=2, следовательно
Так как высоты пирамид SАВС и SMNC совпадают, то VSMNC = VSАВС : 4= 34:4=8,5 Ответ. 8,5 |
Задача № 6
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
|
|
Дано: SABCD – пирамида; ABCD – прямоугольник; АВ=3; ВС = 4; VSABCD = 16 Найти: H Решение: V= SАВСD = АВ 16= Ответ. 4 |
Задача № 7
Сторона основания правильной четырехугольной пирамиды равна 6 см, боковая грань наклонена к плоскости основания под углом 60°. Найти объем пирамиды.
см, боковая грань наклонена к плоскости основания под углом 60°. Найти объем пирамиды.
|
|
Дано: SABCD – правильная четырехугольная пирамида; АВ=6 Найти: VSABCD Решение: VSABCD = Sосн = AB2; Sосн = (6
SO – высота пирамиды;
Н=SО = 9см; VSABCD = Ответ. 324 см3 |
Задача № 8
Основанием пирамиды является прямоугольник со сторонами 6см и 8см. Все боковые ребра равны 13 см. Найти объём пирамиды.
|
|
Дано: SABCD – пирамида; ABCD – прямоугольник; АВ=6см; ВС = 8си; SA=SB=SC=SD=13cм. Найти: VSABCD Решение: VSABCD = SАВСD = АВ
АС2 = АВ2 + ВС2 ; АС2 = 62 + 82 =100; АС=10; AO=5см SO SO2 = АS2 – AO2 ; SO2 = 132 – 52 =169-25=144; SO=12см Н=SO VSABCD = Ответ. 192см3 |
Задача № 9
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны
2см, а объем равен  см3.
см3.
|
|
Дано: SABC-правильная треугольная пирамида; АВ=2см; VSABC = Найти: Н Решение: VSABC =
SABC =
Ответ. 3 |
Задача № 10
Стороны оснований правильной четырехугольной усеченной пирамиды равны 3см и 5см. Найдите объем пирамиды, если ее боковое ребро равно 2 см и наклонено к плоскости основания под углом 60 градусов.
см и наклонено к плоскости основания под углом 60 градусов.
|
|
Дано: ABCDA1B1C1D1-правильная усеченная четырехугольная пирамида; АВ=5см; A1B1 = 3 см; DD1 = 2
Найти: V Решение: V= S1 =
D1F = 2 V= Ответ. 49 см3 |
Задания для самостоятельного решения
1. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна  .
.
2. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
4. Основанием прямой призмы является ромб со стороной 12см и углом 60º. Меньшее из диагональных сечений призмы является квадратом. Найти объем призмы.
5. В кубе AD1 через середину ребер АВ, DС и вершину D1 проведено сечение. Найдите объем куба, если площадь этого сечения равна  .
.
![]()
Для вас очередная статья, сегодня мы мы рассмотрим задания с параллелепипедом. Освежим в памяти само понятие…
Параллелепипед — это четырехугольная призма, все грани которой — параллелограммы. Параллелепипеды, как и призмы, могут быть прямыми и наклонными.
Если сказать просто, то у прямого параллелепипеда его боковые рёбра перпендикулярны основанию, боковые грани прямоугольники, основания параллелограммы; у наклонного параллелепипеда верхнее и нижнее основания как бы смещены параллельным сдвигом, посмотрите рисунок в первой задаче.
В предыдущих статьях мы рассматривали задачи с прямоугольным параллелепипедом (все грани прямоугольники). Представленные ниже задания я выделил в отдельную группу, так как в ходе решения рассматривается пирамида — стоят вопросы о нахождении её объёма. Решаются они практически устно, но мы их разберём подробно. Что нужно помнить?
Объём параллелепипеда формула

С площадью основания всё ясно. А что такое высота? Если параллелепипед прямой, то понятно – его высота равна боковому ребру. Если же параллелепипед наклонный? Его высота равна расстоянию между основаниями, то есть простыми словами можно сказать, что это длина отрезка, который перпендикулярен основаниям и соединяет их:

Но в данных задачах находить саму площадь основания и высоту будет не нужно.
Формула объёма пирамиды:

*Запомните навсегда, что объём пирамиды равен одной трети объёма параллелепипеда с тем основанием и высотой.
Рассмотрим задачи:

Объем параллелепипеда равен 9. Найдите объем треугольной пирамиды ABDA1.

Известно, что объём параллелепипеда равен произведению площади его основания и высоты, то есть:

Объём пирамиды равен:
![]()
Рассмотрим пирамиду ABDA1, её высота равна высоте параллелепипеда, так она у них общая. Площадь её основания в два раза меньше площади основания параллелепипеда, так как диагональ BD делит параллелограмм ABCD на два равных по площади треугольника, значит:

Следовательно:

Получили, что объём пирамиды в шесть раз меньше объёма параллелепипеда и будет равен 9:6 = 1,5.
Ответ: 1,5
*В подобных заданиях, где дан объём параллелепипеда и требуется найти объём какой-либо составляющей его части, не нужно пытаться найти саму площадь основания или высоту. Необходимо просто установить соотношение объёмов используя известные свойства.

Объем куба равен 94. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.
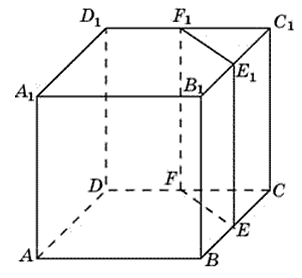
Объем призмы равен произведению площади основания на высоту:
![]()
Поскольку высота призмы равна высоте куба, то их объемы пропорциональны площадям их оснований. Определим, как соотносятся площади оснований призмы и куба.
Пусть ребро куба равно а. Тогда площадь основания куба равна а2.
Определим площадь основания призмы:

Видно, что площадь основания построенной призмы в 8 раз меньше площади основания куба, поэтому искомый объем призмы также будет в 8 раз меньше объёма куба, то есть:

Ответ: 12

Объем куба равен 123. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Объем пирамиды равен:

Площади оснований куба и пирамиды равны, высота пирамиды в два раза меньше ребра куба. Обозначим ребро куба как a, тогда объём пирамиды:

Ответ: 20,5

Объем параллелепипеда ABCDA1B1C1D1 равен 3,6. Найдите объем треугольной пирамиды B1AD1C.

Данную задачу можно решить разными способами. Можно найти площадь основания AD1C и высоту пирамиды (отрезок соединяющий центр куба и вершину B1), но это долгий путь. Проще поступить следующим образом.
Искомый объем равен разности объемов параллелепипеда и четырех пирамид:

То есть мы как бы вычленяем (вырезаем) пирамиду из куба «отсекая» лишнее. Обозначим для простоты восприятия рёбра следующим образом, пусть:
AB = a BC = b BB1 = c
Тогда

Ответ: 1,2

Найдите объем параллелепипеда ABCDA1B1C1D1, если объем треугольной пирамиды ABDA1 равен 10.

Эта задача обратная той, которую мы рассмотрели в самом начале. Мы установили, что объём такой пирамиды в шесть раз меньше объёма параллелепипеда, значит объём параллелепипеда будет равен 60.
Запишем подробнее. Объем параллелепипеда равен:

Объём данной пирамиды равен:

Площадь основания пирамиды равна половине площади основания параллелепипеда, то есть:

Следовательно

Можем записать:

Ответ: 60
![]()
27182. Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC. Ответ: 2

27183. Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

Посмотреть решение
27184. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Посмотреть решение
27209. Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1.

Посмотреть решение
77154. Найдите объем параллелепипеда ABCDA1B1C1D1, если объем треугольной пирамиды ABDA1 равен 3.

Посмотреть решение
Как вы поняли, главное в подобных заданиях знать свойства. Например, что диагональ параллелограмма делит его на два равных по площади треугольника; две диагонали параллелограмма разбивают его на четыре равных по площади треугольника; то, что центр куба делит его высоту пополам, равноотстоит от его граней и вершин и прочее.
Понимая это и другие простые свойства фигур вы без труда вычислите (устно) во сколько раз объём пирамиды будет меньше объёма куба или параллелепипеда, а также сможете быстро решать другие подобные задания.
Например, решим такую задачу: дан наклонный параллелепипед, его основание и основание пирамиды находятся в одной плоскости. Площадь основания пирамиды в 4 раза меньше, её высота в 3 раза меньше высоты параллелепипеда. Найдите объём пирамиды, если объём параллелепипеда равен 360.
Сразу отметим, что у пирамиды с тем же основанием и высотой объём в три раза меньше. Сказанной, что площадь её основания в 4 раза меньше, то есть объём уменьшается ещё в 4 раза, и высота в 3 раза, получаем:

Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Содержание:
Ранее вы уже знакомились с призмой, т. е. многогранником, две грани которого — равные 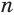
Что такое призма
Равные грани-многоугольники призмы лежат в параллельных плоскостях и называются основаниями призмы, а остальные грани-параллелограммы — боковыми гранями. Ребра боковых граней, не принадлежащие основаниям, называют боковыми ребрами. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называют диагональю призмы (рис. 1). Плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани, называется диагональной плоскостью, а сечение призмы диагональной плоскостью — диагональным сечением. На рисунке 2 показаны два диагональных сечения призмы.
Призмы разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Призма, изображенная на рисунке 1, — шестиугольная, а на рисунке 2, — девятиугольная.
Отличают прямые и наклонные призмы в зависимости от того, перпендикулярны или не перпендикулярны боковые ребра призмы ее основаниям. Обычно при изображении прямой призмы ее боковые ребра проводят вертикально.
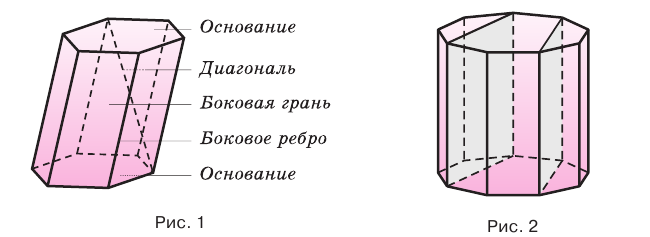
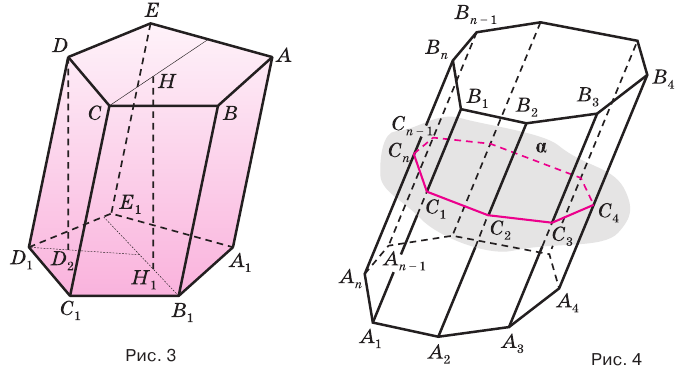
Прямая призма, основаниями которой являются правильные многоугольники, называется правильной призмой. В прямой призме все боковые грани — прямоугольники, а в правильной — равные прямоугольники.
Перпендикуляр, проведенный из какой-либо точки одного основания призмы к плоскости другого основания, называется высотой призмы. На рисунке 3 показаны две высоты 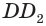 и
и 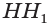 призмы
призмы 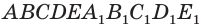 . У прямой призмы ее высота равна боковому ребру.
. У прямой призмы ее высота равна боковому ребру.
Боковые грани составляют боковую поверхность призмы, а боковые грани вместе с основаниями — полную поверхность призмы.
Теорема 1.
Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра:
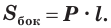
Доказательство:
Пусть имеется 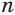 -угольная призма
-угольная призма 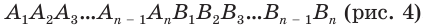 . Пересечем ее плоскостью
. Пересечем ее плоскостью 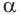 , перпендикулярной боковому ребру. Получим перпендикулярное сечение
, перпендикулярной боковому ребру. Получим перпендикулярное сечение 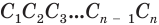 , стороны которого перпендикулярны сторонам параллелограммов, составляющим боковую поверхность призмы. Поэтому для боковой поверхности
, стороны которого перпендикулярны сторонам параллелограммов, составляющим боковую поверхность призмы. Поэтому для боковой поверхности 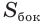 получим:
получим:
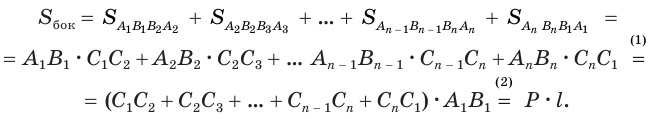
При переходе (1) мы учли, что все боковые ребра призмы равны друг другу, при переходе (2) — то, что сумма  выражает периметр
выражает периметр 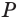 перпендикулярного сечения призмы, а множитель
перпендикулярного сечения призмы, а множитель 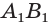 — длину
— длину 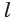 бокового ребра.
бокового ребра.
Следствие 1.
Площадь боковой поверхности прямой призмы равна произведению периметра ее основания и высоты.
Действительно, перпендикулярное сечение прямой призмы равно ее основанию, а боковое ребро является высотой.
Частным видом призмы является параллелепипед, т. е. призма, основанием которой является параллелограмм. Параллелепипед, как и призма, может быть прямым или наклонным. Прямой параллелепипед, основаниями которого являются прямоугольники, называется прямоугольным параллелепипедом. Прямоугольный параллелепипед, у которого три ребра, выходящие из одной вершины, равны друг другу, называется кубом.
У параллелепипеда все грани — параллелограммы, из которых у прямого параллелепипеда прямоугольниками являются боковые грани, а у прямоугольного параллелепипеда — все грани.
12 ребер параллелепипеда разделяются на три четверки равных ребер (рис. 5), его 6 граней — на три пары равных граней (рис. 6), а 4 диагонали пересекаются в одной точке, являющейся центром симметрии параллелепипеда (рис. 7).
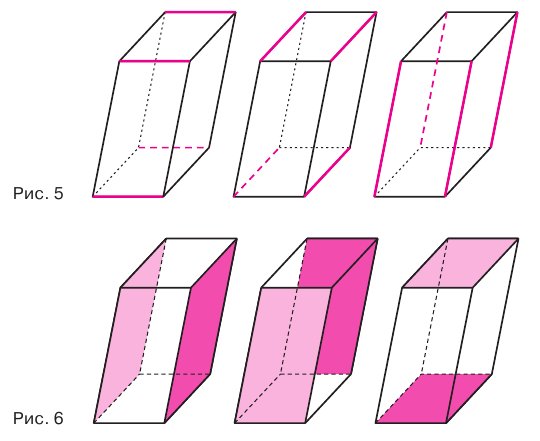
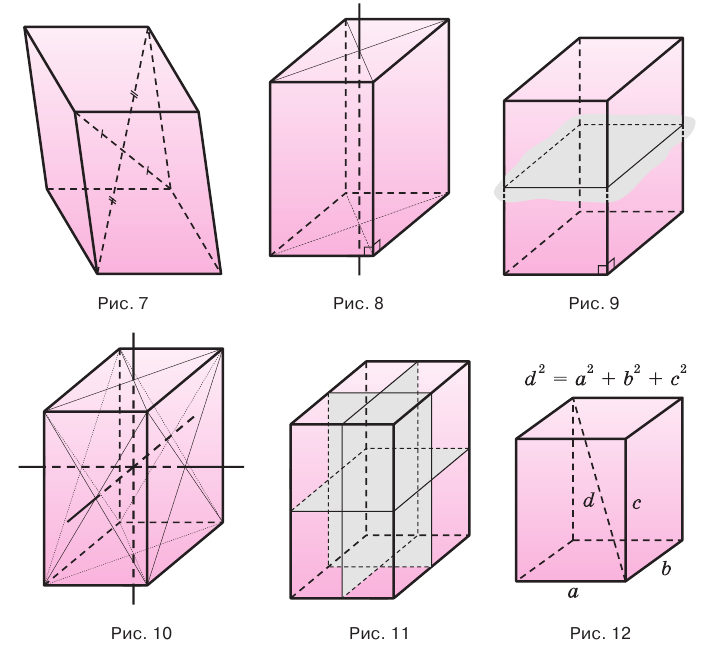
Прямой параллелепипед еще имеет ось симметрии (рис. 8) и плоскость симметрии (рис. 9). Прямоугольный параллелепипед имеет три оси симметрии (рис. 10) и три плоскости симметрии (рис. 11).
Ребра прямоугольного параллелепипеда, выходящие из одной вершины, называют измерениями прямоугольного параллелепипеда. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (рис. 12), и все его диагонали равны друг другу.
Важной характеристикой плоской фигуры является ее площадь. Подобной характеристикой тела является его объем. Будем считать, что изучаемые нами тела имеют объем.
За единицу объема принимают объем куба с ребром 1. На практике пользуются разными единицами объема: как метрическими — кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр, кубический километр, так и неметрическими — галлон, барель, бушель, кварта.
Для объема тела выполняются его основные свойства:
- равные тела имеют равные объемы;
- если тело разделено на части, то его объем равен сумме объемов этих частей.
При этом равными фигурами называют фигуры, которые преобразуются друг в друга определенным движением. Например, равными являются две шестиугольные правильные призмы, у которых соответственно равны стороны оснований и высоты (рис. 13), или два цилиндра с соответственно равными радиусами оснований и образующими (рис. 14). Тело, изображенное на рисунке 15, можно разделить на цилиндр и конус, и его объем равен сумме объемов этих цилиндра и конуса.
Два тела с равными объемами называют равновеликими телами. Равные тела являются равновеликими, но не наоборот.
Вы знаете, что объем 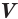 прямоугольного параллелепипеда равен произведению трех его измерений
прямоугольного параллелепипеда равен произведению трех его измерений 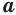 ,
, 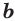 ,
, 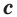 (рис. 16):
(рис. 16): 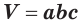 .
.
Учитывая, что в формуле 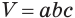 произведение
произведение 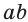 выражает площадь
выражает площадь 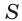 основания прямоугольного параллелепипеда, а число
основания прямоугольного параллелепипеда, а число 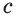 — его высоту
— его высоту 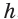 , получим, что объем
, получим, что объем 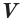 прямоугольного параллелепипеда равен произведению площади его основания и высоты:
прямоугольного параллелепипеда равен произведению площади его основания и высоты:  .
.
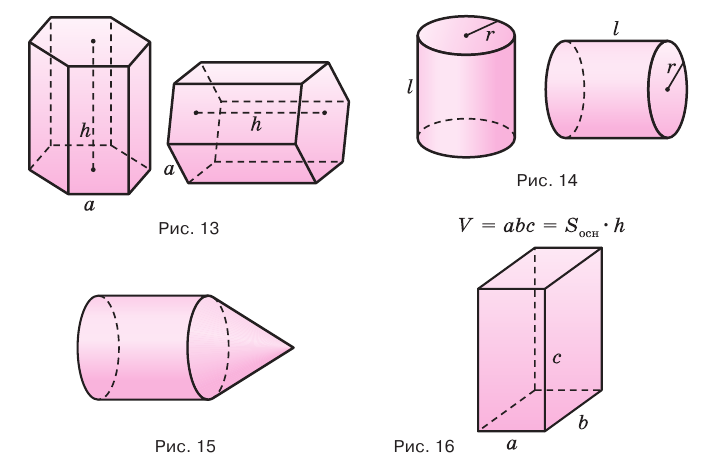
Теорема 2.
Объем произвольного параллелепипеда равен произведению площади его основания и высоты:
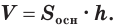
Доказательство:
Пусть имеется произвольный параллелепипед 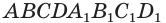 (рис. 17). Через ребро
(рис. 17). Через ребро 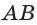 проведем плоскость, перпендикулярную ребру
проведем плоскость, перпендикулярную ребру 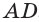 , она отсечет от параллелепипеда треугольную призму
, она отсечет от параллелепипеда треугольную призму 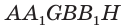 (рис. 18). После параллельного сдвига этой призмы в направлении отрезка
(рис. 18). После параллельного сдвига этой призмы в направлении отрезка 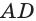 получим призму
получим призму 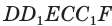 . Параллелепипед
. Параллелепипед 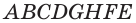 равновелик с данным параллелепипедом
равновелик с данным параллелепипедом 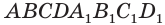 . Выполненное преобразование параллелепипеда также сохраняет объем параллелепипеда, площадь его основания и высоту.
. Выполненное преобразование параллелепипеда также сохраняет объем параллелепипеда, площадь его основания и высоту.
У параллелепипеда 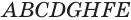 его боковые грани
его боковые грани 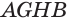 и
и  перпендикулярны плоскости основания. К граням
перпендикулярны плоскости основания. К граням 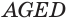 и
и 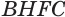 , которые не перпендикулярны плоскости основания, применим такое же преобразование, в результате которого получим прямой параллелепипед
, которые не перпендикулярны плоскости основания, применим такое же преобразование, в результате которого получим прямой параллелепипед 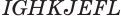 (рис. 19), в котором сохраняются объем, площадь основания и высота.
(рис. 19), в котором сохраняются объем, площадь основания и высота.
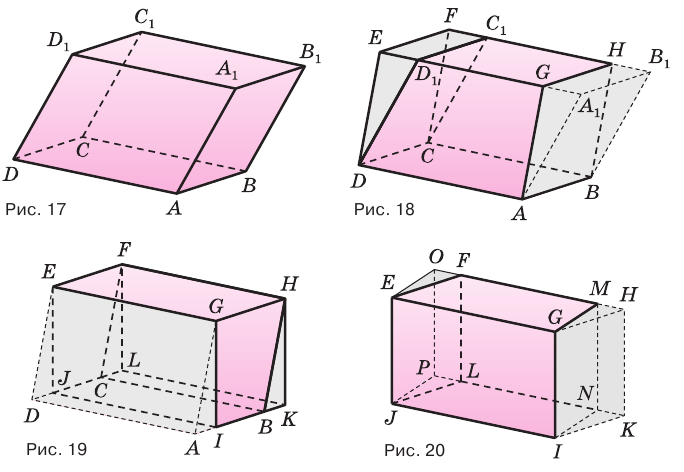
Наконец, применив еще раз такое преобразование к граням 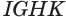 и
и  прямого параллелепипеда
прямого параллелепипеда 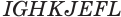 , получим прямоугольный параллелепипед
, получим прямоугольный параллелепипед 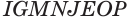 (рис. 20), сохранив объем параллелепипеда, площадь его основания и высоту.
(рис. 20), сохранив объем параллелепипеда, площадь его основания и высоту.
Значит,
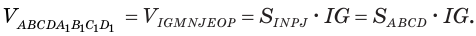
Множитель 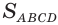 есть площадь основания параллелепипеда
есть площадь основания параллелепипеда 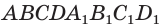 , а множитель
, а множитель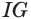 выражает его высоту, так как
выражает его высоту, так как 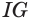 есть перпендикуляр, возведенный из точки
есть перпендикуляр, возведенный из точки 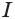 основания
основания 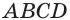 к другому основанию
к другому основанию 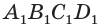 . Значит, объем произвольного параллелепипеда равен произведению площади его основания и высоты.
. Значит, объем произвольного параллелепипеда равен произведению площади его основания и высоты.
Теорема 3.
Объем призмы равен произведению площади ее основания и высоты:
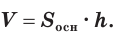
Доказательство:
Рассмотрим сначала треугольную призму 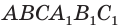 (рис. 21). Дополним ее до параллелепипеда
(рис. 21). Дополним ее до параллелепипеда 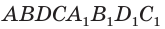 (рис. 22). Точка
(рис. 22). Точка 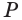 пересечения диагоналей диагонального сечения
пересечения диагоналей диагонального сечения 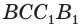 этого параллелепипеда является его центром симметрии. Это означает, что достроенная призма
этого параллелепипеда является его центром симметрии. Это означает, что достроенная призма 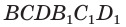 симметрична данной призме
симметрична данной призме 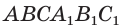 относительно центра
относительно центра 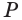 , а потому эти призмы равны друг другу. Значит, объем параллелепипеда
, а потому эти призмы равны друг другу. Значит, объем параллелепипеда 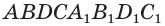 равен удвоенному объему данной призмы.
равен удвоенному объему данной призмы.
Объем параллелепипеда 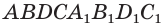 равен произведению площади его основания
равен произведению площади его основания 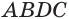 и высоты. Но площадь его основания
и высоты. Но площадь его основания 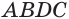 равна удвоенной площади основания
равна удвоенной площади основания 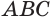 данной призмы, а высота параллелепипеда равна высоте призмы.
данной призмы, а высота параллелепипеда равна высоте призмы.
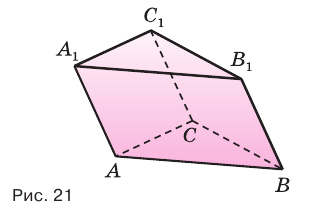
Отсюда следует, что объем призмы 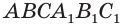 равен площади ее основания
равен площади ее основания 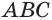 и высоты. Теперь рассмотрим произвольную призму
и высоты. Теперь рассмотрим произвольную призму 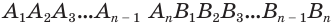 (рис. 23).
(рис. 23).
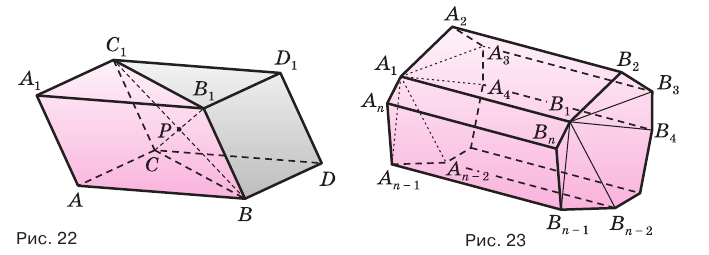
Диагональными сечениями, проходящими через вершину 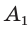 , разобьем ее на треугольные призмы-части
, разобьем ее на треугольные призмы-части 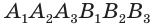 ,
, 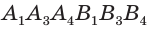 , …,
, …, 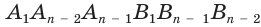 ,
, 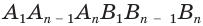 , которые все имеют одну и ту же высоту, равную высоте
, которые все имеют одну и ту же высоту, равную высоте 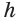 данной призмы. Объем данной призмы равен сумме объемов призм-частей. По уже доказанному для объема
данной призмы. Объем данной призмы равен сумме объемов призм-частей. По уже доказанному для объема 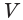 данной призмы получим:
данной призмы получим:
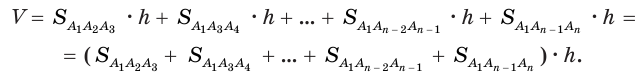
Учитывая, что сумма в скобках выражает площадь S основания данной призмы, получим:
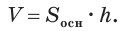
Следствие 2.
Объем прямой призмы равен произведению площади ее основания и бокового ребра.
Призма и её сечения
С призмой вы уже знакомы. Несмотря на это, мы напомним определение призмы и её свойства.
Призма -это многогранник, две грани которого равные n-угольники (основания), лежащие в параллельных плоскостях, а остальные n граней – параллелограммы (рис. 22).
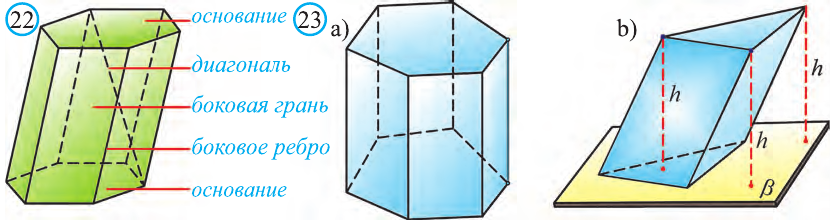
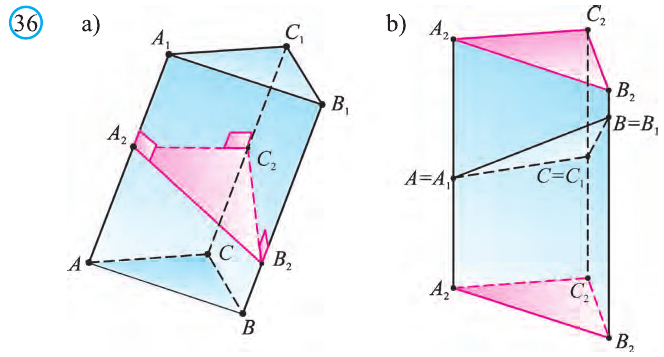
В зависимости от того перпендикулярны ли боковые грани призмы его основаниям или нет, призмы делят на прямые или наклонные. На рисунке 23.а изображена прямая призма, а на рисунке 23.b – наклонная. Очевидно, что боковые грани прямой призмы – прямоугольники.
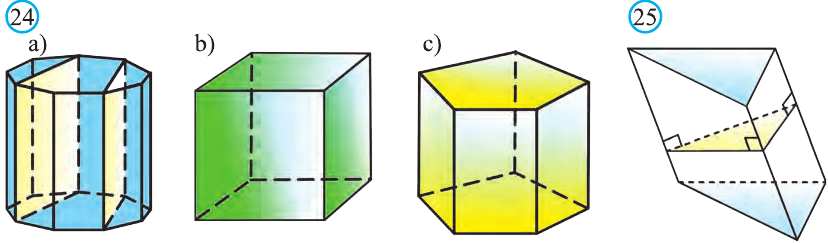
Если основания прямой призмы являются правильными многоугольниками, то её называют правильной (рис. 24). Боковые грани правильной призмы это равные между собой прямоугольники.
Перпендикуляр, опущенный из некоторой точки одного основания к другому, называют его перпендикуляром (рис. 23.b).
Сечение призмы, проходящее через соответствующие диагонали его оснований, называют диагональным сечением (рис. 24.а) и их число равно числу диагоналей одного из оснований.
Перпендикулярным сечением призмы называют сечение перпендикулярное всем его боковым рёбрам (рис. 25). так как 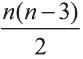 число диагоналси выпуклого n-угольника, то число диагональных сeчeний n-угольной призмы также равно
число диагоналси выпуклого n-угольника, то число диагональных сeчeний n-угольной призмы также равно 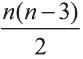 .
.
В каждом диагональном сечении призмы можно провести две диагонали. Следовательно, n-угольная призма имеет 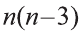 диагоналей.
диагоналей.
Пример:
В наклонной треугольной призме расстояния между боковыми ребрами соответственно равны 7 см, 15 см и 20 см. Найдите расстояние между большей боковой гранью и противолежащим боковым ребром.
Решение:
Известно, что расстояние между параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки одной прямой на другую. Тогда длины сторон перпендикулярного сечения ABC (рис. 26). Наибольшая грань призмы проходит через наибольшую сторону АС= 20 см этого сечения. Расстояние от рёбра призмы В2В1 до плоскости грани 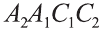 равно высоте BD треугольника ABC.
равно высоте BD треугольника ABC.
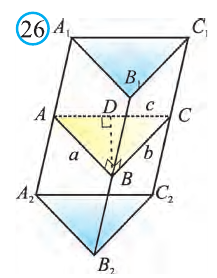
Тогда по формуле Герона получаем:
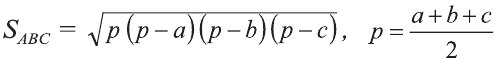
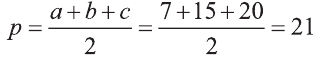 ,
,
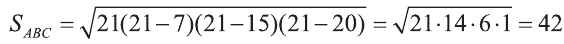 .
.
С другой стороны, 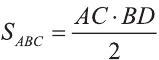 .
.
Отсюда 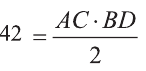 или
или 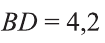 см.
см.
Ответ: 4,2 см.
Параллелепипед и куб
Призма, основаниями которой являются параллелограммы, называют параллелепипедом (рис. 27). Параллелепипеды также как и призмы могут быть прямыми (рис. 27.а) и наклонными (рис. 27.b). 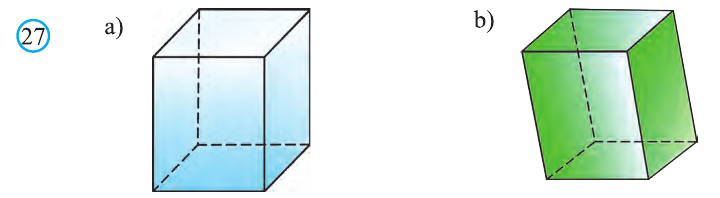
Грани параллелепипеда, не имеющие общую вершину, называют противоположными гранями.
У параллелепипеда:
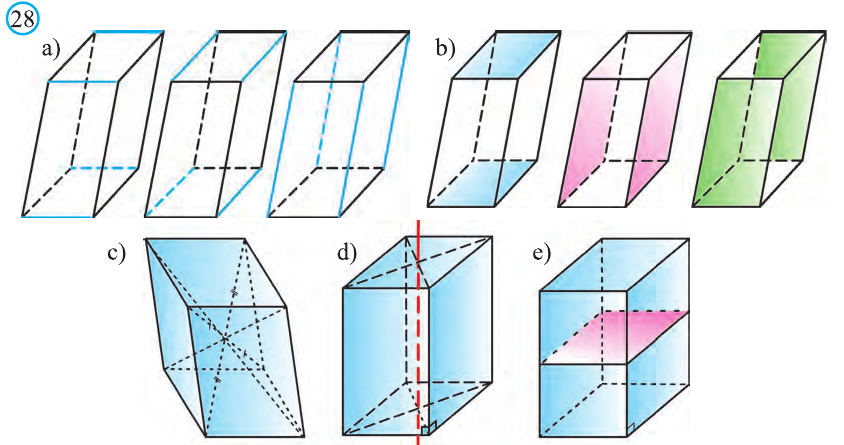
- —12 рёбер, каждые четыре из которых равны (рис. 28.а),
- —6 граней, которые попарно параллельны и равны (рис. 28.b),
- —4 диагонали, которые пересекаются и точкой пересечения делятся пополам (рис. 28.с),
- —точка пересечения диагоналей – центр его симметрии (рис. 28.с). Прямой параллелепипед имеет ось симметрии (рис. 28.d) и плоскость симметрии (рис. 28.e).
Прямой параллелепипед, основания которого являются прямоугольники, называют прямоугольным параллелепипедом (рис. 29). Очевидно, что все грани прямоугольного параллелепипеда являются прямоугольниками.
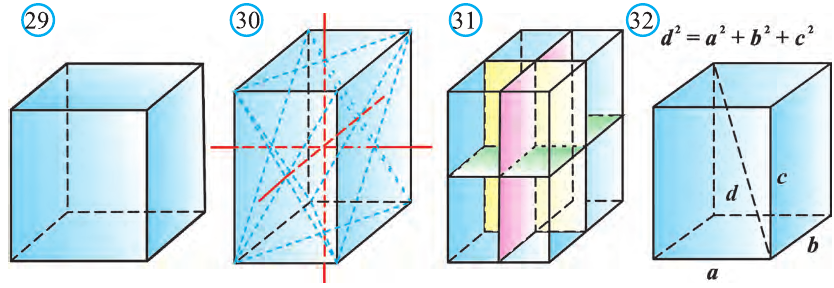
Прямоугольный параллелепипед имеет три оси симметрии (рис. 30) и три плоскости симметрии (рис. 31).
Длины трех рёбер, исходящих из одной вершины прямоугольного параллелепипеда называют его измерениями.
Свойство: В прямоугольном параллелепипеде квадрат любой диагонали d равен сумме квадратов его измерений: а, b и с (рис.32):
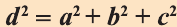 .
.
Прямоугольный параллелепипед, все измерения которого равны, называют кубом. Очевидно, что все грани куба являются равными квадратами. Куб имеет один центр симметрии, 9 осей симметрии и 9 плоскостей симметрии.
Выше были перечислены свойства призмы. Некоторые из них были показаны в 10 классе. Доказательства остальных свойств проще, поэтому их доказательства вы можете провести самостоятельно.
Площади боковой и полной поверхности призмы
На рисунке 33 проведены высоты НН1 DD1 призмы
АВСDЕ–А1В1С1D1Е1. Очевидно, что высоты правильной призмы будут равны её боковому рёбру. 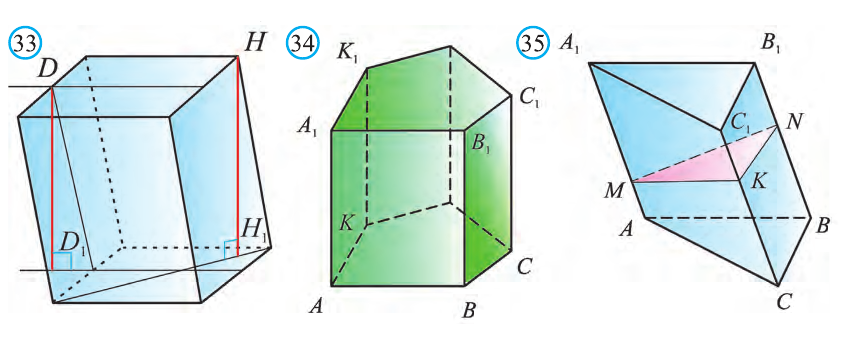
Боковая поверхность призмы (точнее, площадь боковой поверхности)равна сумме боковых поверхностей ее граней, а полная поверхнасть равна сумме боковой поверхности и площадей двух ее оснований. 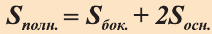
Теорема. Боковая поверхность прямой призмы равна произведению периметра ее основания на высоту: 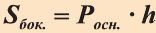
Доказательство. Пусть высота данной прямой призмы равна 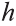 , а периметр основания
, а периметр основания 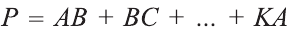 (рис. 34). Известно, что каждая грань прямой призмы является прямоугольником. Основания прямоугольников равны соответствующим сторонам основания призмы, а высоты равны высоте призмы.
(рис. 34). Известно, что каждая грань прямой призмы является прямоугольником. Основания прямоугольников равны соответствующим сторонам основания призмы, а высоты равны высоте призмы.
Тогда 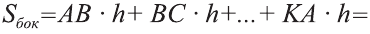
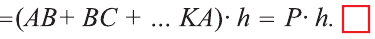
Теорема. Боковая поверхность произвольной призмы равна произведению периметра перпендикулярного сечения призмы на ее боковое ребро: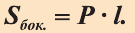
Доказательство. Пусть периметр перпендикулярного сечения призмы равен Р (рис. 35). Сечение делит призму на две части (рис. 36.а). Совершим параллельный перенос одной из этих частей так, чтобы основания нашей призмы совпали. В результате мы получим новую прямую призму (рис. 36.b). Очевидно, что, боковая поверхность этой призмы равна боковой поверхности данной. Её основанием является перпендикулярное сечение, а боковое ребро равно 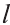 .
.
Тогда по доказанной выше теореме: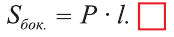
Объем призмы
Одним из свойств, характеризующих геометрические тела в пространстве, является понятие объема. Каждый предмет (тело) занимает некоторую часть пространства. Например, кирпич по сравнению со спичечным коробком занимает большую часть пространства. Для сравнения этих частей между собой вводится понятие объёма.
Объём – это величина, численное значение которой обладает следующими свойствами:
- Любое тело имеет определённый объём, выраженный положительным числом.
- Равные тела имеют равные объёмы.
- Если тело разбито на несколько частей, то его объём равен сумме объёмов этих частей.
- Объём куба, ребро которого равно единице, равен единице.
Объём – также как длина и площадь, является величиной. В зависимости от выбора единицы длины, объём единого куба измеряют в кубических единицах:
1 см3, 1 дм3, 1 м3 и т. д.
Объёмы тел измеряют различными способами или вычисляют. Например, объёмы маленьких предметов можно измерить с помощью сосудов (мензурки) с мелкими делениями (шкалами) (рис. 46). А объём ведра можно измерить с помощью сосуда, имеющего единичный объём, наполнив его водой (рис. 47). Но таким способом мы не можем измерить объёмы всех тел. В таких случаях объём вычисляют различными способами. Ниже рассмотрим их без доказательств. 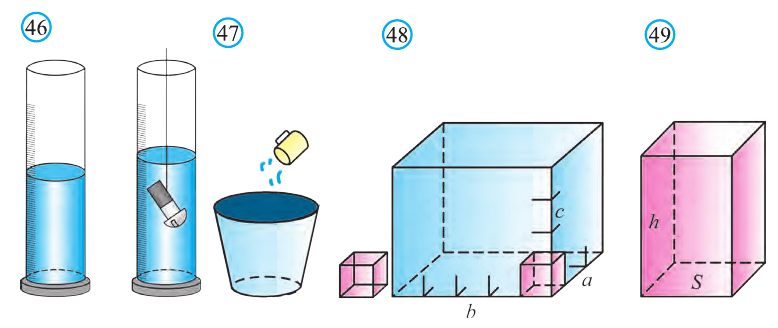
Объём параллелепипеда
Теорема. Объём прямоугольного параллелепипеда равен произведению трех его измерeний (рис.48): 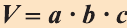 .
.
Следствие. Объём прямоугольного параллелепипеда равен произведению площади его основания на высоту (рис. 49): 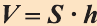 .
.
Теорема. Объём произвольного параллелепипеда равен произведению площади его основания на высоту (рис. 50): 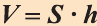 .
.
Это свойство вытекает из вышеупомянутого следствия. На рисунке 50 показано как данный параллелепипед преобразовать в прямоугольный параллелепипед. Воспользовавшись этим самостоятельно обоснуйте свойство. 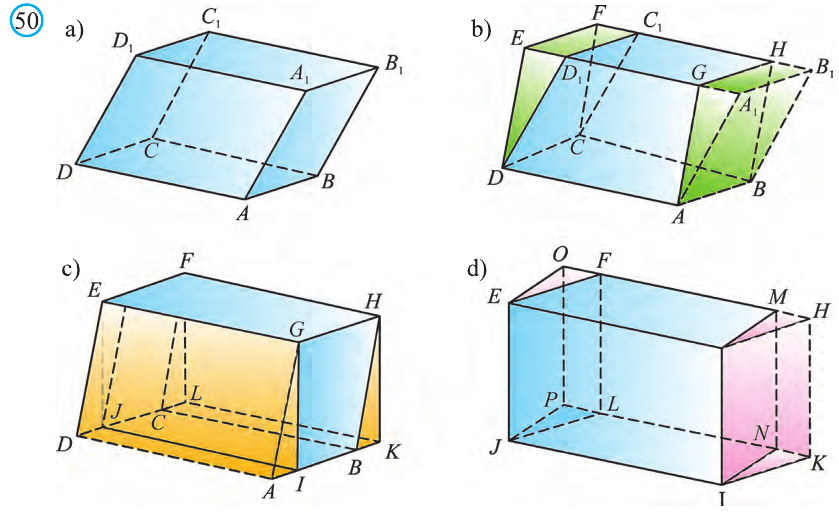
Нахождение объёма призмы
Теорема. Объём прямой призмы равен произведению площади его основания на высоту (рис. 51): 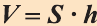 .
.
Доказательство. 1 случай. Пусть основанием призмы будет прямоугольный треугольник (рис 51.а). Эту призму можно дополнить равной ей призмой до прямоугольного параллелепипеда (рис. 51 .b).
Если объём данной призмы, площадь её основания и высота V, S и h, то объём полученного прямоугольного параллелепипеда, площадь его основания и высота будут соответственно равны 2V, 2S и h.
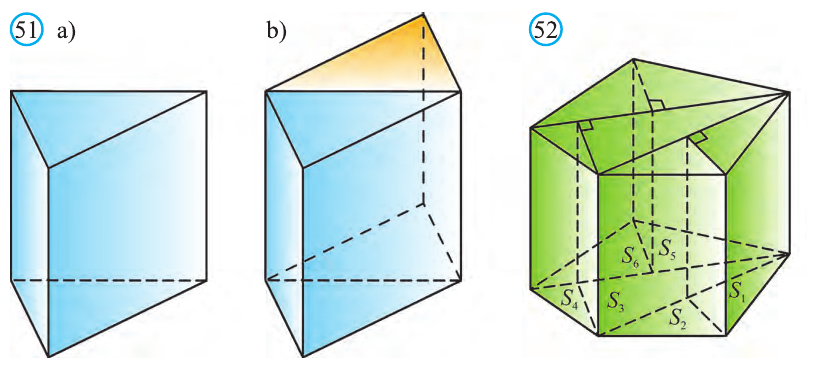
Следовательно 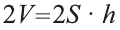 или
или 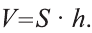
2 случай. Пусть S – площадь произвольной n – угольной прямой призмы и h – её высота. Основание призмы – n-угольник делится диагоналями на треугольники, каждый из которых можно разделить на прямоугольные треугольники (рис. 52). В результате данная призма разделится на конечное число прямых призм, основания которых являются прямоугольными треугольниками. Высоты этих призм равны h , а сумма площадей оснований этих призм равна площади основания данной призмы: 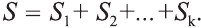
Объём данной призмы равен сумме объёмов составляющих её треугольных призм:
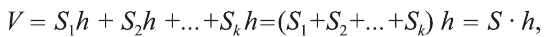
или 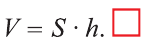
Теорема. Объём произвольной призмы равен произведению площади его основания на высоту: 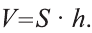
По рисунку 5.3 докажите эту теорему самостоятельно, сначала для треугольной призмы (рис. 5.3.а), затем для любой призмы (рис. 5.3.b).
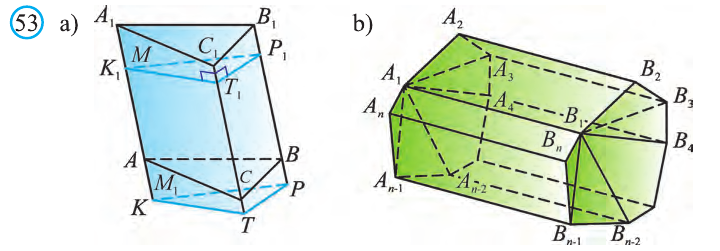
Пример:
Стороны основания прямого параллелепипеда равны а и b, а угол между ними 30°. Найдите его объём, если площадь его боковой поверхности равна S.
Решение:
Обозначим высоту параллелепипеда h(рис. 54).
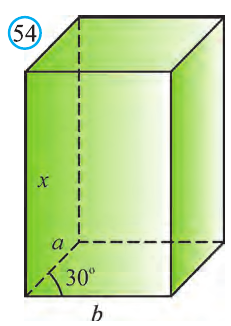
Тогда по условию задачи:
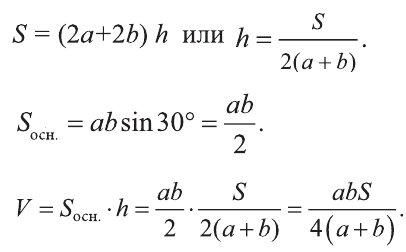
- Цилиндр в геометрии
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии
- Возникновение геометрии
- Геометрические преобразования в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление















































