Как найти объем усеченного конуса по высоте

{V=dfrac {1}{3} pi h (R_1^2 + R_1 cdot R_2 + R_2^2)}

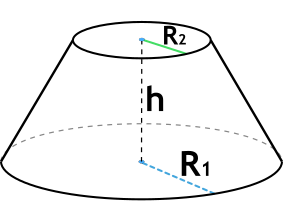
Радиус нижнего основания R₁

Радиус верхнего основания R₂

Усеченный конус – фигура, которую можно получить из конуса, если через него провести сечение, параллельное основанию.

Справедливо и другое определение.

Усеченный конус – тело вращения, которое получается при вращении прямоугольной трапеции вокруг меньшей боковой стороны.

Калькулятор объема конуса и формулы для расчета находится здесь.

Чтобы найти объем усеченного конуса необходимо знать три его характеристики – высоту (h), радиус нижнего основания (R₁) и радиус верхнего основания (R₂). Кроме того существует вторая формула объема усеченного конуса, для которой необходимо знать высоту конуса, а также площади его верхнего и нижнего оснований.

Содержание:

калькулятор объема усеченного конуса
формула объема усеченного конуса через радиусы оснований и высоту
формула объема усеченного конуса через площади оснований и высоту
примеры задач

Формула объема усеченного конуса через радиусы оснований и высоту

{V=dfrac {1}{3} pi h (R_1^2 + R_1 cdot R_2 + R_2^2)}

h – высота усеченного конуса

R₁ – радиус нижнего основания

R₂ – радиус верхнего основания

Формула объема усеченного конуса через площади оснований и высоту

{V=dfrac {h}{3} (S_1 + sqrt{S_1 cdot S_2} + S_2)}

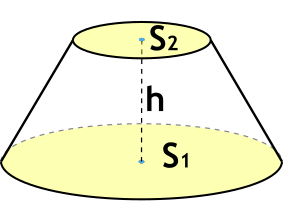
h – высота усеченного конуса

S₁ – площадь нижнего основания

S₂ – площадь верхнего основания

Примеры задач на нахождение объема усеченного конуса

Задача 1

Найдите объем усеченного конуса радиусы оснований которого равны 1см и 2см, а высота равна 3см.

Решение

Для решения используем формулу объема усеченного конуса через высоту и радиусы оснований. Подставим известные нам значения в формулу и произведем расчет.

V=dfrac {1}{3} pi h (R_1^2 + R_1 cdot R_2 + R_2^2) = dfrac {1}{3} pi cdot 3 cdot (2^2 + 2 cdot 1 + 1^2) = dfrac {1}{3} pi cdot 3 cdot (4 + 2 + 1) = dfrac {1}{3} pi cdot 3 cdot 7 = dfrac {1}{3} pi cdot 21 = dfrac {21}{3} pi = 7 pi : см^3 approx 21.99115 : см^3

Ответ: 7 pi : см^3 approx 21.99115 : см^3

Полученный ответ легко проверить с помощью калькулятора .

Источник

Как рассчитать объем усеченного конуса

На данной странице калькулятор поможет рассчитать объем усеченного конуса онлайн. Для расчета задайте высоту и радиус. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.

Усеченный конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

Через радиусы и высоту

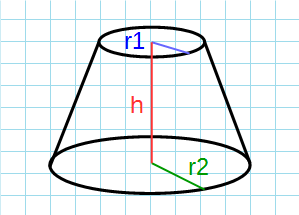
Формула объема усеченного конуса через радиусы и высоту:

π – константа равная (3.14); r1 – радиус верхнего основания ; r2 – радиус нижнего основания; h – высота усеченного конуса.

Источник

Определение усеченного конуса

Усеченный конус можно получить из обычного конуса, если пересечь такой конус плоскостью, параллельной основанию. Тогда та фигура, которая находится между двумя плоскостями (этой плоскостью и основание обычного конуса) и будет называться усеченным конусом.

У него имеется два основания, которые для кругового конуса являются кругами, причем один из них больше другого. Также усеченный конус имеет высоту — отрезок, соединяющий два основания и перпендикулярный каждому из них.

Онлайн-калькулятор объема усеченного конуса

Усеченный конус может быть прямым, тогда у него центр одного основания проецируется в центр второго. Если конус наклонный, то такое проецирование не имеет места.

Рассмотрим прямой круговой конус. Объем данной фигуры может быть рассчитан несколькими способами.

Формула объема усеченного конуса через радиусы оснований и расстояние между ними

Если нам дан круговой усеченный конус, то найти его объем можно по формуле:

Объем усеченного конуса

V=13⋅π⋅h⋅(r12+r1⋅r2+r22)V=frac{1}{3}cdotpicdot hcdot(r_1^2+r_1cdot r_2+r_2^2)

r1,r2r_1, r_2 — радиусы оснований конуса;
hh — расстояние между этими основаниями (высота усеченного конуса).

Рассмотрим пример.

Задача 1

Найдите объем усеченного конуса, если известно, что площадь малого основания равна 64π см264pitext{ см}^2, большого — 169π см2169pitext{ см}^2, а высота его равна 14 см14text{ см}.

Решение

S1=64πS_1=64pi
S2=169πS_2=169pi
h=14h=14

Найдем радиус малого основания:

S1=π⋅r12S_1=picdot r_1^2

64π=π⋅r1264pi=picdot r_1^2

64=r1264=r_1^2

r1=8r_1=8

Аналогично, для большого основания:

S2=π⋅r22S_2=picdot r_2^2

169π=π⋅r22169pi=picdot r_2^2

169=r22169=r_2^2

r2=13r_2=13

Вычислим объем конуса:

V=13⋅π⋅h⋅(r12+r1⋅r2+r22)=13⋅π⋅14⋅(82+8⋅13+132)≈4938 см3V=frac{1}{3}cdotpicdot hcdot (r_1^2+r_1cdot r_2+r_2^2)=frac{1}{3}cdotpicdot14cdot(8^2+8cdot 13+13^2)approx4938text{ см}^3

Ответ

4938 см3.4938text{ см}^3.

Формула объема усеченного конуса через площади оснований и их расстояние до вершины

Пусть у нас есть усеченный конус. Мысленно добавим к нему недостающий кусок, тем самым делая из него “обычный конус” с вершиной. Тогда объем усеченного конуса можно найти как разность объемов двух конусов с соответствующими основаниями и их расстоянием (высотой) до вершины конуса.

Объем усеченного конуса

V=13⋅S⋅H−13⋅s⋅h=13⋅(S⋅H−s⋅h)V=frac{1}{3}cdot Scdot H-frac{1}{3}cdot scdot h=frac{1}{3}cdot (Scdot H-scdot h)

SS — площадь основания большого конуса;
HH — высота этого (большого) конуса;
ss — площадь основания малого конуса;
hh — высота этого (малого) конуса;

Задача 2

Определите объем усеченного конуса, если высота полного конуса HH равна 10 см10text{ см}, радиус нижнего основания RR — 5 см5text{ см}, верхнего rr — 4 см4text{ см}, а высота усеченного конуса – 8 см8text{ см}.

Решение

R=5R=5
r=4r=4
H=10H=10
H−h=8H-h=8,
где hh — высота малого конуса.

Найдем площади обоих оснований конуса:

S=π⋅R2=π⋅52≈78.5S=picdot R^2=picdot 5^2approx78.5

s=π⋅r2=π⋅42≈50.24s=picdot r^2=picdot 4^2approx50.24

Найдем высоту малого конуса hh:

H−h=8H-h=8

h=H−8h=H-8

h=10−8h=10-8

h=2h=2

Объем равен по формуле:

V=13⋅(S⋅H−s⋅h)≈13⋅(78.5⋅10−50.24⋅2)≈228 см3V=frac{1}{3}cdot (Scdot H-scdot h)approxfrac{1}{3}cdot (78.5cdot 10-50.24cdot 2)approx228text{ см}^3

Ответ

228 см3.228text{ см}^3.

На Студворк вы можете заказать решение задач на заказ онлайн у профильных экспертов!

Тест по теме “Объем усеченного конуса”

Источник

Объем и площадь усеченного конуса

Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.

Радиус основания 1

см

Радиус основания 2

см

Высота

см

Размерность

Раcсчитать

Что считает калькулятор?

Калькулятор объема и площади усеченного конуса — это онлайн инструмент, который используется для быстрого расчета объема и площади усеченного конуса по его радиусам большего и меньшего оснований и высоте. Объем такого конуса представляет собой объем пространства, которое занимает эта фигура в трехмерном пространстве.

Калькулятор объема и площади усеченного конуса может быть полезным инструментом для учебных заданий или практических задач, связанных с расчетами объемов и площадей таких геометрических фигур. Он также может использоваться в различных профессиональных областях, где необходимы точные расчеты объемов и площадей, например, в архитектуре, инженерии, физике и т.д.

Где можно применить калькулятор объема и площади усеченного конуса?

Калькулятор объема и площади усеченного конуса может применяться в различных сферах, включая:

Инженерия и строительство: усеченный конус может использоваться в качестве формы для создания конструкций и деталей, таких как колонны, башни, фонари, вазы и т.д. такие расчеты помогают определить необходимое количество материала для изготовления детали.
Производство: усеченный конус может использоваться в качестве формы для изготовления различных изделий из металла, стекла, керамики, пластика и т.д. Расчёт его параметров помогает определить необходимое количество сырья для производства изделия.
Математика: усеченный конус может быть использован для примеров и задач в математическом образовании. Расчёт объёма и площади позволяет ученикам узнать, как применять формулы для нахождения объёма и площади фигур.
Машиностроение: усеченный конус может использоваться в качестве детали для различных механизмов и машин. Расчёт объёма и площади помогает определить размеры и форму детали.
Архитектура и дизайн: усеченный конус может использоваться в качестве элемента декора и оформления интерьера и экстерьера зданий. Расчёт объёма и площади помогает определить оптимальный размер и форму элемента декора.

В чем преимущество усеченного конуса как геометрической фигуры?

Усеченный конус — это геометрическая фигура, у которой основаниями являются две круглые плоскости, соединенные боковой поверхностью, которая имеет форму конуса, но сечение вдоль его высоты меньше его оснований.

Преимущества этой геометрической фигуры могут включать:

Усеченный конус имеет большую устойчивость, чем обычный конус, так как он имеет большую поверхность опоры на основаниях, что делает его лучшим выбором для некоторых приложений, например, при проектировании оболочек реакторов.
Усеченный конус может быть более экономичным в использовании материала, чем обычный конус, так как он имеет меньшую высоту, но сохраняет ту же площадь оснований. Это может быть полезно в проектировании строительных элементов, таких как колонны или башни.
Усеченный конус может иметь большую универсальность в применении, так как его форма может быть изменена путем изменения размеров его оснований и высоты. Это позволяет использовать усеченные конусы в различных областях, например, в качестве башенной опоры или формы для литья металла.
Усеченный конус может иметь более эргономичную форму, что делает его удобным в использовании в некоторых приложениях, например, при проектировании мебели или автомобильных деталей.
Усеченный конус может иметь более интересный внешний вид, что делает его привлекательным для использования в художественном дизайне или архитектуре.

В целом, усеченный конус является полезной геометрической фигурой, которая имеет множество преимуществ в различных областях применения.

Как вычислить объем усеченного конуса через радиусы его оснований и высоту?

Для расчета объема усеченного конуса необходимо знать радиусы большего и меньшего оснований, а также высоту усеченного конуса.

Формула для расчета объема усеченного конуса:

V = (1/3) * π * h * (R² + Rr + r²)

где:

π – число Пи (3.14)
V – объем усеченного конуса
h – высота усеченного конуса
R – радиус большего основания
r – радиус меньшего основания

Чтобы использовать эту формулу, нужно знать значения h, R и r. Затем необходимо подставить значения в формулу и выполнить вычисления.

Пример:

Допустим, у нас есть усеченный конус с высотой 10 см, радиусом большего основания 6 см и радиусом меньшего основания 4 см. Чтобы найти объем усеченного конуса, мы можем использовать формулу:

V = (1/3) * π * h * (R² + Rr + r²)
V = (1/3) * 3,14 * 10 * (6^2 + 6*4 + 4^2)
V = 795,5 см³

Ответ: объем усеченного конуса равен 795,5 кубическим сантиметрам.

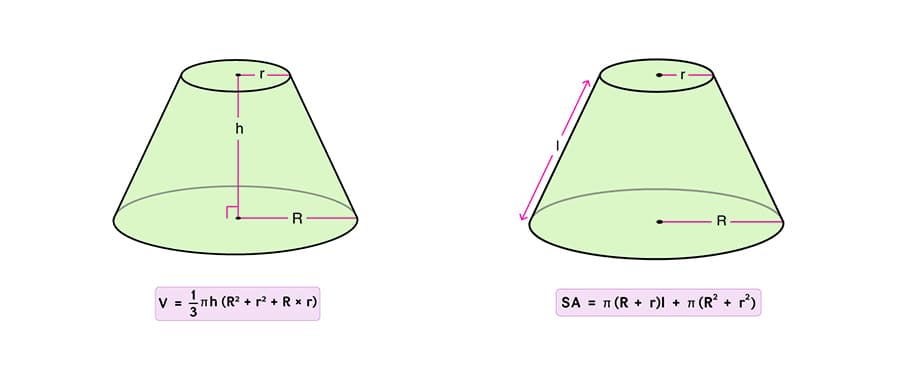
Как вычислить площадь усеченного конуса через радиусы его оснований и образующую?

Площадь усеченного конуса можно рассчитать с использованием следующей формулы:

S = π(r + R)ℓ + π(R² + r²)

где S – площадь усеченного конуса,
π – математическая константа, примерно равная 3.14,
r1 и r2 – радиусы оснований большего и меньшего конусов соответственно,
и ℓ – образующая, т.е. расстояние между вершиной и основанием, вычисленная по теореме Пифагора.

Для решения задачи необходимо знать значения радиусов оснований и образующей. Если известны только высоты обоих конусов, то необходимо использовать теорему Пифагора для вычисления образующей.

После подстановки всех известных значений в формулу можно вычислить площадь усеченного конуса.

❓ Вопросы и ответы

А вот несколько ответов на часто задаваемы вопросе о шаре и его объеме.

Как пользоваться онлайн калькулятором объема и площади усеченного конуса?

Для того, чтобы использовать калькулятор объема усеченного конуса, нужно ввести значения радиусов его оснований и высоту в соответствующие поля калькулятора, затем калькулятор автоматически рассчитает объем шара. Для расчёта площади нужно проделать соответствующие действия со значениями радиусов оснований и образующей, которая вычисляется по теореме Пифагора.

Что такое усеченный конус?

Усеченный конус – это геометрическое тело, полученное из обычного конуса путем удаления верхней части тела параллельным срезом, расположенным на определенном расстоянии от вершины конуса.

Для чего нужен расчет объема усеченного конуса?

Расчет объема и площади усеченного конуса может быть полезен во многих областях, включая инженерию, архитектуру, производство и технику. Например, в производственной отрасли расчет объема и площади усеченного конуса может помочь определить количество материалов, необходимых для создания детали.

Какой материал лучше всего подходит для изготовления усеченных конусов?

Для изготовления усеченного конуса можно использовать различные материалы в зависимости от требований к конструкции. Однако, наиболее распространенными материалами для изготовления усеченных конусов являются металлы. Это может быть сталь, алюминий, медь, латунь и другие металлы. Металлические конусы обычно используются в технических приложениях, где требуется высокая прочность и устойчивость к износу.

Как вычислить образующую усеченного конуса?

Образующая конуса (l) может быть найдена с помощью теоремы Пифагора, для этого можно воспользоваться формулой: l = √((R – r)² + h²). Таким образом, чтобы вычислить образующую усеченного конуса, необходимо знать значения радиуса большего основания, радиуса меньшего основания и высоты конуса, после чего следует применить формулу, описанную выше.

Формула вычисления объема усеченного конуса

Чтобы найти объем прямого усеченного кругового конуса, нужно знать оба радиуса его оснований и высоту.

R/r – радиусы оснований;
h – высота конуса.

Примечание: в расчетах значение числа π обычно округляется до 3,14.

Пример задачи

Высота усеченного кругового конуса равна 9 см, а радиусы его оснований – 4 см и 7 см. Найдите объем данной фигуры.

Решение

Воспользуемся приведенной выше формулой, подставив в нее известные значения:

Источник