From Wikipedia, the free encyclopedia
| Uniform triangular prism | |
|---|---|

|
|
| Type | Prismatic uniform polyhedron |
| Elements | F = 5, E = 9 V = 6 (χ = 2) |
| Faces by sides | 3{4}+2{3} |
| Schläfli symbol | t{2,3} or {3}×{} |
| Wythoff symbol | 2 3 | 2 |
| Coxeter diagram | |
| Symmetry group | D3h, [3,2], (*322), order 12 |
| Rotation group | D3, [3,2]+, (322), order 6 |
| References | U76(a) |
| Dual | Triangular dipyramid |
| Properties | convex |
 Vertex figure 4.4.3 |

3D model of a (uniform) triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases, and square sides.
Equivalently, it is a polyhedron of which two faces are parallel, while the surface normals of the other three are in the same plane (which is not necessarily parallel to the base planes). These three faces are parallelograms. All cross-sections parallel to the base faces are the same triangle.
As a semiregular (or uniform) polyhedron[edit]
A right triangular prism is semiregular or, more generally, a uniform polyhedron if the base faces are equilateral triangles, and the other three faces are squares. It can be seen as a truncated trigonal hosohedron, represented by Schläfli symbol t{2,3}. Alternately it can be seen as the Cartesian product of a triangle and a line segment, and represented by the product, The dual of a triangular prism is a triangular bipyramid.
The symmetry group of a right 3-sided prism with triangular base is D3h of order 12. The rotation group is D3 of order 6. The symmetry group does not contain inversion.
Volume[edit]
The volume of any prism is the product of the area of the base and the distance between the two bases. In this case the base is a triangle so we simply need to compute the area of the triangle and multiply this by the length of the prism:
where b is the length of one side of the triangle, h is the length of an altitude drawn to that side, and l is the distance between the triangular faces.
Truncated triangular prism[edit]
A truncated right triangular prism has one triangular face truncated (planed) at an oblique angle.[1]
The volume of a truncated triangular prism with base area A and the three heights h1, h2, and h3 is determined by
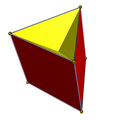
Facetings[edit]
There are two full D3h symmetry facetings of a triangular prism, both with 6 isosceles triangle faces, one keeping the original top and bottom triangles, and one the original squares. Two lower C3v symmetry facetings have one base triangle, 3 lateral crossed square faces, and 3 isosceles triangle lateral faces.
| Convex | Facetings | |||
|---|---|---|---|---|
| D3h symmetry | C3v symmetry | |||

|
|

|

|
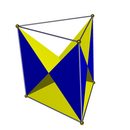
|
| 2 {3} 3 {4} |
3 {4} 6 ( ) v { } |
2 {3} 6 ( ) v { } |
1 {3} 3 t'{2} 6 ( ) v { } |
1 {3} 3 t'{2} 3 ( ) v { } |
Related polyhedra and tilings[edit]

Family of uniform n-gonal prisms
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prism name | Digonal prism | (Trigonal) Triangular prism |
(Tetragonal) Square prism |
Pentagonal prism | Hexagonal prism | Heptagonal prism | Octagonal prism | Enneagonal prism | Decagonal prism | Hendecagonal prism | Dodecagonal prism | … | Apeirogonal prism |
| Polyhedron image | … | ||||||||||||
| Spherical tiling image | Plane tiling image | ||||||||||||
| Vertex config. | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | … | ∞.4.4 |
| Coxeter diagram | … |
| n | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| Schläfli symbol | {2} || t{2} | {3} || t{3} | {4} || t{4} | {5} || t{5} | {6} || t{6} | {7} || t{7} | {8} || t{8} |
| Cupola |  Digonal cupola |
 Triangular cupola |
 Square cupola |
 Pentagonal cupola |
 Hexagonal cupola (Flat) |
 Heptagonal cupola (Non-regular face) |
 Octagonal cupola (Non-regular face) |
| Related uniform polyhedra |
Triangular prism |
Cubocta- hedron |
Rhombi- cubocta- hedron |
Rhomb- icosidodeca- hedron |
Rhombi- trihexagonal tiling |
Rhombi- triheptagonal tiling |
Rhombi- trioctagonal tiling |
Symmetry mutations[edit]
This polyhedron is topologically related as a part of sequence of uniform truncated polyhedra with vertex configurations (3.2n.2n), and [n,3] Coxeter group symmetry.
*n32 symmetry mutation of truncated tilings: t{n,3}
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | ||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]… |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | |
| Truncated figures |

|

|

|

|

|

|

|

|

|

|
|
| Symbol | t{2,3} | t{3,3} | t{4,3} | t{5,3} | t{6,3} | t{7,3} | t{8,3} | t{∞,3} | t{12i,3} | t{9i,3} | t{6i,3} |
| Triakis figures |

|

|

|

|

|

|

|
||||
| Config. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ |
This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
| *n32 symmetry mutation of expanded tilings: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paracomp. | ||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]… |
*∞32 [∞,3] |
|
| Figure | 
|

|

|

|

|

|

|
|
| Config. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Compounds[edit]
There are 4 uniform compounds of triangular prisms:
- Compound of four triangular prisms, compound of eight triangular prisms, compound of ten triangular prisms, compound of twenty triangular prisms.
Honeycombs[edit]
There are 9 uniform honeycombs that include triangular prism cells:
- Gyroelongated alternated cubic honeycomb, elongated alternated cubic honeycomb, gyrated triangular prismatic honeycomb, snub square prismatic honeycomb, triangular prismatic honeycomb, triangular-hexagonal prismatic honeycomb, truncated hexagonal prismatic honeycomb, rhombitriangular-hexagonal prismatic honeycomb, snub triangular-hexagonal prismatic honeycomb, elongated triangular prismatic honeycomb
[edit]
The triangular prism is first in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (equilateral triangles and squares in the case of the triangular prism). In Coxeter’s notation the triangular prism is given the symbol −121.
| k21 figures in n dimensional | ||||||||
|---|---|---|---|---|---|---|---|---|
| Space | Finite | Euclidean | Hyperbolic | |||||
| En | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Coxeter group |
E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 =  = E8+ = E8+
|
E10 =  = E8++ = E8++
|
| Coxeter diagram |
||||||||
| Symmetry | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] |
| Order | 12 | 120 | 1,920 | 51,840 | 2,903,040 | 696,729,600 | ∞ | |
| Graph | 
|

|

|

|

|

|
– | – |
| Name | −121 | 021 | 121 | 221 | 321 | 421 | 521 | 621 |
Four dimensional space[edit]
The triangular prism exists as cells of a number of four-dimensional uniform 4-polytopes, including:
| Four dimensional polytopes with triangular prisms | |||||||
|---|---|---|---|---|---|---|---|
| Tetrahedral prism |
Octahedral prism |
Cuboctahedral prism |
Icosahedral prism |
Icosidodecahedral prism |
Truncated dodecahedral prism |
||

|

|

|

|

|

|
||
| Rhomb-icosidodecahedral prism |
Rhombi-cuboctahedral prism |
Truncated cubic prism |
Snub dodecahedral prism |
n-gonal antiprismatic prism |
|||

|

|

|

|

|
|||
| Cantellated 5-cell |
Cantitruncated 5-cell |
Runcinated 5-cell |
Runcitruncated 5-cell |
Cantellated tesseract |
Cantitruncated tesseract |
Runcinated tesseract |
Runcitruncated tesseract |

|

|

|

|

|

|

|

|
| Cantellated 24-cell |
Cantitruncated 24-cell |
Runcinated 24-cell |
Runcitruncated 24-cell |
Cantellated 120-cell |
Cantitruncated 120-cell |
Runcinated 120-cell |
Runcitruncated 120-cell |

|

|

|

|

|

|

|

|
See also[edit]
- Wedge (geometry)
References[edit]
- ^ Kern, William F.; Bland, James R. (1938). Solid Mensuration with proofs. p. 81. OCLC 1035479.
- Weisstein, Eric W. “Triangular prism”. MathWorld.
- Interactive Polyhedron: Triangular Prism
- Surface area and volume of a triangular prism

Определение площади поверхности и объема усеченных цилиндров и призм
Джон Рэй Куэвас
Что такое усеченный цилиндр?
Усеченный круговой цилиндр, также известный как цилиндрический сегмент, представляет собой твердое тело, образованное пропусканием непараллельной плоскости через круговой цилиндр. Некруглое верхнее основание наклонено к круглому сечению. Если круговой цилиндр является правильным цилиндром, то каждая правая часть представляет собой круг, имеющий такую же площадь, что и основание.
Пусть K – площадь правого сечения, а h 1 и h 2 – самый короткий и самый длинный элемент усеченного цилиндра соответственно. Объем усеченного кругового цилиндра определяется формулой, приведенной ниже. Если усеченный цилиндр представляет собой правильный круговой цилиндр радиуса r, объем можно выразить через радиус.
V = K
V = πr 2

Усеченные цилиндры
Джон Рэй Куэвас
Что такое усеченная призма?
Усеченная призма – это часть призмы, образованная путем прохождения плоскости, не параллельной основанию и пересекающей все боковые края. Поскольку плоскость усечения не параллельна основанию, сформированное твердое тело имеет два непараллельных основания, которые являются многоугольниками с одинаковым количеством ребер. Боковые края не совпадают, а боковые грани представляют собой четырехугольники (прямоугольники или трапеции). Если отрезанная призма – это правая призма, то боковые грани – правильные трапеции. Общая площадь поверхности усеченной призмы – это сумма площадей двух многоугольных оснований и правых трапециевидных граней.
В общем, объем усеченной призмы равен произведению площади ее правого сечения на среднее значение длин ее боковых краев. K – площадь правого сечения, L – средняя длина боковых краев. Для усеченной призмы правильное сечение равно площади основания. Объем усеченной призмы определяется формулой ниже. K – это B, умноженное на значение sinθ, L равно средней длине его боковых краев, а n – количество сторон основания.
V = KL
V = BL

Усеченные призмы
Джон Рэй Куэвас
Задача 1. Площадь поверхности и объем усеченной треугольной призмы.
Усеченная правая призма имеет равностороннее треугольное основание, одна сторона которого составляет 3 сантиметра. Боковые края имеют длину 5 см, 6 см и 7 см. Найдите общую площадь поверхности и объем усеченной правой призмы.

Площадь и объем усеченной треугольной призмы.
Джон Рэй Куэвас
Решение
а. Так как это усеченная справа призма, все боковые грани перпендикулярны нижнему основанию. Это делает каждую боковую грань призмы правильной трапецией. Вычислить для ребер AC, AB и BC верхнего основания, используя заданные в задаче меры.
AC = √3 2 + (7-5) 2
AC = √13 сантиметров
АВ = √3 2 + (7-6) 2
AB = √10 сантиметров
BC = √3 2 + (6-5) 2
AB = √10 сантиметров
б. Вычислите площадь треугольника ABC и треугольника DEF, используя формулу Герона.
s = (a + b + c) / 2
s = (√13 + √10 + √10) / 2
s = 4,965
АВС = √4.965 (4,965 – √13) (4,965 – √10) (4,965 – √10)
A ABC = 4,68 см 2
A DEF = 1/2 (3) 2 (sin (60 °))
A DEF = 3,90 см 2
c. Вычислите площадь трапециевидных граней.
ACED = 1/2 (7 + 5) (3)
A ACED = 18 см 2
BCEF = 1/2 (6 + 5) (3)
BCEF = 16,5 см 2
ABFD = 1/2 (7 +6) (3)
A ABFD = 19,5 см 2
d. Найдите общую площадь усеченной призмы, суммируя все площади.
TSA = B 1 + B 2 + LSA
TSA = 4,68 + 3,90 + 18 +16,5 +19,5
TSA = 62,6 см 2
е. Найдите объем усеченной правой призмы.
V = BL
V = 3,90
V = 23,4 см 3
Окончательный ответ: общая площадь поверхности и объем усеченной правой призмы, приведенные выше, составляют 62,6 см 2 и 23,4 см 3 соответственно.
Задача 2: объем и поперечная площадь усеченной прямоугольной призмы
Найдите объем и поперечную площадь усеченной прямоугольной призмы с краем основания 4 фута. Боковые края имеют размеры 6 футов, 7 футов, 9 футов и 10 футов.

Объем и поперечная площадь усеченной прямоугольной призмы.
Джон Рэй Куэвас
Решение
а. Поскольку это прямоугольная усеченная призма, все боковые грани перпендикулярны нижнему основанию. Это делает каждую боковую грань призмы правильной трапецией. Вычислите края верхнего квадратного основания, используя указанные в задаче меры.
S 1 = √4 2 + (10-9) 2
S 1 = √17 футов
S 2 = √4 2 + (9-6) 2
S 2 = 5 футов
S 3 = √4 2 + (7-6) 2
S 3 = √17 футов
S 4 = √4 2 + (10-7) 2
S 4 = 5 футов
б. Вычислите площадь трапециевидных граней.
А 1 = 1/2 (10 + 9) (4)
A 1 = 38 футов 2
А 2 = 1/2 (9 + 6) (4)
A 2 = 30 футов 2
А 3 = 1/2 (7 +6) (4)
А 3 = 26 футов 2
А 4 = 1/2 (7 + 10) (4)
А 4 = 34 фута 2
c. Вычислите общую боковую площадь, получив сумму всех площадей боковых поверхностей.
TLA = А 1 + А 2 + А 3 + А 4
TLA = 38 + 30 + 26 + 34
TLA = 128 футов 2
е. Найдите объем усеченной прямоугольной призмы.
V = BL
V = 4 2
V = 128 футов 3
Окончательный ответ: общая площадь поверхности и объем усеченной правой квадратной призмы, приведенные выше, составляют 128 футов 2 и 128 футов 3 соответственно.
Задача 3: объем правого кругового цилиндра
Покажите, что объем усеченного правого кругового цилиндра равен V = πr 2.

Объем правого кругового цилиндра.
Джон Рэй Куэвас
Решение
а. Упростите все переменные данной формулы для объема. B обозначает площадь основания, а h 1 и h 2 обозначают самый короткий и самый длинный элементы усеченного цилиндра, показанного выше.
B = площадь круглого основания
B = πr 2
б. Разделите усеченный цилиндр на два твердых тела так, чтобы клиновая часть имела объем, равный половине объема верхнего цилиндра высотой h 2 – h 1. Объем верхнего цилиндра обозначен V 1. С другой стороны, нижняя часть представляет собой цилиндр высотой h 1 и объемом V 2.
V = (1/2) V 1 + V 2
V 1 = B (h 2 – h 1)
V 2 = B xh 1
V = (1/2) (B (h 2 – h 1)) + (B xh 1)
V = (1/2) (B xh 2) – (1/2) (B xh 1) + (B xh 1)
V = B
V = πr 2
Окончательный ответ: объем усеченного правого кругового цилиндра равен V = πr 2.
Задача 4: Полная площадь поверхности усеченной прямоугольной призмы
Блок земли в виде усеченной правой призмы имеет квадратное основание с размером ребер 12 сантиметров. Два смежных боковых края имеют длину 20 см каждый, а два других боковых края имеют длину 14 см каждый. Найдите общую площадь поверхности блока.

Общая площадь усеченной прямоугольной призмы.
Джон Рэй Куэвас
Решение
а. Поскольку это прямоугольная усеченная призма, все боковые грани перпендикулярны нижнему основанию. Это делает каждую боковую грань призмы правильной трапецией. Вычислите края верхнего квадратного основания, используя указанные в задаче меры.
S 1 = √12 2 + (20-20) 2
S 1 = 12 сантиметров
S 2 = √12 2 + (20 – 14) 2
S 2 = 6√5 сантиметров
S 3 = √12 2 + (14 – 14) 2
S 3 = 12 сантиметров
S 4 = √12 2 + (20 – 14) 2
S 4 = 6√5 сантиметров
б. Вычислите площадь нижнего квадратного основания и верхнего прямоугольного основания.
ВЕРХНИЙ = 12 х 6√5
ВЕРХНИЙ = 72√5 см 2
НИЖНИЙ = 12 х 12
НИЖНИЙ = 144 см 2
б. Вычислите площадь прямоугольной и трапециевидной граней данной усеченной прямоугольной призмы.
А 1 = 20 х 12
A 1 = 240 см 2
А 2 = 1/2 (20 + 14) (12)
A 2 = 204 см 2
А 3 = 14 х 12
А 3 = 168 см 2
А 4 = 1/2 (20 + 14) (12)
А 4 = 204 см 2
d. Найдите общую площадь поверхности усеченной квадратной призмы, суммируя все площади.
TSA = ВЕРХНИЙ + НИЖНИЙ + LSA
TSA = 72√5 + 144 + 240 + 204 + 168 + 204
TSA = 1120,10 см 2
Окончательный ответ: Общая площадь поверхности данной усеченной квадратной призмы составляет 1120,10 см 2.
Другие темы о площади поверхности и объеме
- Как рассчитать приблизительную площадь фигур неправильной формы с помощью правила Симпсона 1/3
Узнайте, как приблизить площадь фигур неправильной формы с помощью правила 1/3. В этой статье рассматриваются концепции, проблемы и решения о том, как использовать правило Симпсона 1/3 для аппроксимации площади.
- Как вычислить
площадь поверхности и объем призм и пирамид Это руководство научит вас определять площадь поверхности и объем различных многогранников, таких как призмы, пирамиды. Есть примеры, чтобы показать вам, как решать эти проблемы шаг за шагом.
© 2020 Луч
Треугольная призма — призма с тремя боковыми гранями. Этот многогранник имеет в качестве граней треугольное основание, его копию, полученную в результате параллельного переноса и 3 грани, соединяющие соответствующие стороны[en]. Прямая треугольная призма имеет прямоугольные боковые стороны, в противном случае призма называется косой.
Однородная треугольная призма — это прямая треугольная призма с равносторонним основанием и квадратными боковыми сторонами.
Призма является пятигранником, у которого две грани параллельны, в то время как нормали трёх других лежат в одной плоскости (которая не обязательно параллельна основаниям). Эти три грани являются параллелограммами. Все сечения, параллельные основаниям, являются одинаковыми треугольниками.
Полуправильный (однородный) многогранник[править | править код]
Прямая треугольная призма является полуправильным многогранником или, более обще, однородным многогранником, если основание является правильным треугольником, а боковые стороны — квадратами.
Этот многогранник можно рассматривать как усечённый треугольный осоэдр, представленный символом Шлефли t{2,3}. Его также можно рассматривать как прямое произведение треугольника на отрезок, что представляется как {3}x{}. Двойственным многогранником треугольной призмы является треугольная бипирамида.
Группой симметрии прямой призмы с треугольным основанием является D3h порядка 12. Группой вращения служит D3 с порядком 6. Группа симметрии не содержит центральную симметрию.
Объём[править | править код]
Объём любой призмы равен произведению площади основания на расстояние между основаниями. В нашем случае, когда основание треугольно, нужно просто вычислить площадь треугольника и умножить на длину призмы:
где b — длина стороны основания, h равна высоте треугольника, а l равна расстоянию между треугольниками.
Усечённая треугольная призма[править | править код]
Усечённая прямая треугольная призма имеет одну усечённую треугольную грань[1].
Гранение[править | править код]
Имеется полная D2h симметрия гранений[en] (удаление части многогранника, не создавая новые вершины, пересечение рёбер новоё вершиной не считается) треугольной призмы. Получающиеся многогранники имеются многогранники с 6 гранями в виде равнобедренного треугольника, один многогранник сохраняет исходные верхний и нижний треугольники, и один сохраняет исходные квадраты. Две симметрии гранения C3v имеют один базовый треугольник, 3 грани в виде боковых самопересекающихся квадратов и 3 грани в виде равнобедренных треугольников.
| Выпуклые | Гранение | |||
|---|---|---|---|---|
| Симметрия D3h | Симметрия C3v | |||

|

|

|

|

|
| 2 {3} 3 {4} |
3 {4} 6 () v { } |
2 {3} 6 () v { } |
1 {3} 3 t'{2}[en] 6 () v { } |
1 {3} 3 t'{2}[en] 3 () v { } |
Связанные многогранники и мозаики[править | править код]
| Многоугольник | 
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | ||||||||||||
| Конфигурация | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | 17.4.4 | ∞.4.4 |
| n | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Название | {2} || t{2} | {3} || t{3} | {4} || t{4} | {5} || t{5} | {6} || t{6} |
| Купол |  Диагональный купол |
 Трёхскатный купол |
 Четырёхскатный купол |
 Пятискатный купол |
 Шестискатный купол (плоский) |
| Связанные однородные многогранники |
Треугольная призма |
Кубооктаэдр |
Ромбокубо- октаэдр |
Ромбоикосо- додекаэдр |
Ромботри- шестиугольная мозаика[en] |
Варианты симметрии[править | править код]
Этот многогранник топологически является частью последовательности однородных усечённых многогранников с вершинными конфигурациями (3.2n.2n) и имеющими симметрию [n,3] группы Коксетера.
| Варианты симметрии *n32 усечённых мозаик: 3.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *n32 [n,3] |
Сферическая | Евклидова | Компактная гиперболич. | Параком- пактная |
Некомпактная гиперболич. | ||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]… |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | |
| Усечённые фигуры |

|

|

|

|

|

|

|

|

|

|
|
| Конфигурация | 3.4.4 | 3.6.6 | 3.8.8 | 3.10.10 | 3.12.12[en] | 3.14.14[en] | 3.16.16[en] | 3.∞.∞[en] | 3.24i.24i | 3.18i.18i | 3.12i.12i |
| Разделённые фигуры |

|

|

|

|

|

|
|||||
| Конфигурация | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12[en] | V3.14.14[en] | V3.16.16 | V3.∞.∞ |
Этот многогранник топологически является частью последовательности рёберно усечённых[en] многогранников с вершинной фигурой (3.4.n.4), которая продолжается как умощения гиперболической плоскости. Эти вершинно-транзитивные[en] фигуры имеют зеркальную симметрию[en] (*n32).
| Варианты симметрии *n42 расширенных мозаик: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *n32 [n,3] |
Сферическая | Евклидова | Компактная гиперболическая |
Паракомпактная | ||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]… |
*∞32 [∞,3] |
|
| Фигура | 
|

|

|

|

|

|

|
|
| Конфигурация | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4[en] | 3.4.7.4[en] | 3.4.8.4[en] | 3.4.∞.4[en] |
Составные тела[править | править код]
Имеется 4 однородных составных тела из треугольных призм:
- соединение четырёх треугольных призм[en];
- соединение восьми треугольных призм[en];
- соединение десяти треугольных призм[en];
- соединение двадцати треугольных призм[en].
Соты[править | править код]
Существует 9 однородных сот, которые включают треугольные призмы:
- гироудлинённые альтернированные кубические соты[en]
- удлинённые альтернированные кубические соты[en]
- плосконосые квадратно-призматические соты[en]
- треугольные призматические соты
- тришестиугольные призматические соты
- усечённые шестиугольные призматические соты
- ромботришестиугольные призматические соты
- плосконосые шестиугольные призматические соты
- удлинённые треугольные призматические соты
Связанные многогранники[править | править код]
Треугольная призма является первой в пространственной серии полуправильных многогранников[en]. Каждый последующий однородный многогранник имеет в качестве вершинной фигуры предыдущий многогранник. Торольд Госсет[en] обнаружил эту серию в 1900 году как содержащую все виды граней правильных многомерных многогранников, содержащую все симплексы и ортоплексы (правильные треугольники и квадраты в случае треугольной призмы). В нотации Коксетера[en] треугольной призме соответствует символ −121.
| k21[en] в пространстве размерности n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Пространство | Конечное | Евклидово | Гиперболическое | |||||
| En[en] | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Группа Коксетера |
E₃=A₂A₁ | E₄=A₄ | E₅=D₅ | E₆ | E₇[en] | E₈ | E₉ = Ẽ₈ = E₈+ | E₁₀ = T₈ = E₈++ |
| Диаграмма Коксетера |
||||||||
| Симметрия[en] | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] |
| Порядок | 12 | 120 | 192 | 51 840 | 2 903 040 | 696 729 600 | ∞ | |
| Граф | 
|

|

|

|

|

|
– | – |
| Обозначение | −121 | 021 | 121 | 221[en] | 321[en] | 421[en] | 521[en] | 621[en] |
Четырёхмерное пространство[править | править код]
Треугольная призма существует как ячейка в большом числе четырёхмерных однородных четырёхмерных многогранников[en], включая:
| тетраэдральная призма[en] |
октаэдральная призма[en] |
кубооктаэдрическая призма[en] |
икосаэдральная призма[en] |
икосододекаэдральная призма[en] |
усечённая додекаэдральная призма[en] |
||

|

|

|

|

|

|
||
| Ромбоикосидодекаэдральная призма[en] |
Ромбокубоктаэдральная призма[en] |
Усечённая кубическая призма[en] |
Плосконосая додекаэдральная призма[en] |
n-угольная антипризматическая призма[en] |
|||

|

|

|

|

|
|||
| Рёберноусечённая 5-ячейка[en] |
Кантиусечённая 5-ячейка[en] |
Рансинированная 5-ячейка[en] |
Рансиусечённая 5-ячейка[en] |
Cantellated tesseract |
Кантиусечённый тессеракт[en] |
Рансинированный тессеракт[en] |
Рансиусечённый тессеракт[en] |

|

|

|

|

|

|

|

|
| Кантелированная 24-ячейка[en] |
Кантиусечённая 24-ячейка[en] |
Рансинированная 24-ячейка[en] |
Рансиусечённая 24-ячейка[en] |
Кантелированная 120-ячейка[en] |
Кантиусечённая 120-ячейка[en] |
Рансинированная 120-ячейка[en] |
Рансиусечённая 120-ячейка[en] |

|

|

|

|

|

|

|

|
См. также[править | править код]
- Клин
Примечания[править | править код]
- ↑ William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.81
Ссылки[править | править код]
- Weisstein, Eric W. Triangular prism (англ.) на сайте Wolfram MathWorld.
- Interactive Polyhedron: Triangular Prism
- surface area and volume of a triangular prism
| Равномерная треугольная призма | |
|---|---|

|
|
| Тип | Призматический однородный многогранник |
| Элементы |
F = 5, E = 9 V = 6 (χ = 2) |
| Лица по сторонам | 3 {4} +2 {3} |
| Символ Шлефли | t {2,3} или {3} × {} |
| Символ Wythoff | 2 3 | 2 |
| Диаграмма Кокстера |
|
| Группа симметрии | D 3h , [3,2], (* 322), порядок 12 |
| Группа вращения | D 3 , [3,2] + , (322), порядок 6 |
| использованная литература | U 76 (а) |
| Двойной | Треугольная дипирамида |
| Характеристики | выпуклый |
 Вершинная фигура 4.4.3 |

3D модель (однородной) треугольной призмы
В геометрии , A треугольной призмы является трехгранной призмы ; это многогранник, состоящий из треугольного основания, переведенной копии и трех граней, соединяющих соответствующие стороны . Правая треугольная призма имеет прямоугольные стороны, в противном случае это наклонное . Равномерная треугольная призма является правой треугольной призмой с равносторонними основаниями, и квадратными сторон.
Эквивалентно, это многогранник, две грани которого параллельны, а нормали поверхностей трех других находятся в одной плоскости (которая не обязательно параллельна базовым плоскостям). Эти три грани – параллелограммы . Все поперечные сечения, параллельные граням основания, представляют собой один и тот же треугольник.
Как полуправильный (или равномерный) многогранник
Прямоугольная призма является полуправильной или, в более общем смысле, однородным многогранником, если ее базовые грани представляют собой равносторонние треугольники , а три другие грани – квадраты . Его можно рассматривать как усеченный тригональный осоэдр , представленный символом Шлефли t {2,3}. В качестве альтернативы его можно рассматривать как декартово произведение треугольника и отрезка линии и представлять его как произведение: Двойник треугольной призмы – это треугольная бипирамида .
Группа симметрии правой 3-сторонней призмы с треугольным основанием – это D 3h порядка 12. Группа вращений – это D 3 порядка 6. Группа симметрии не содержит инверсии .
Объем
Объем любой призмы – это произведение площади основания и расстояния между двумя основаниями. В этом случае основание представляет собой треугольник, поэтому нам просто нужно вычислить площадь треугольника и умножить ее на длину призмы:
где b – длина одной стороны треугольника, h – длина высоты, проведенной к этой стороне, а l – расстояние между треугольными гранями.
Усеченная треугольная призма
Усечена правая треугольная призма имеет одну треугольной грань обрезано ( строганые ) под косым углом.
Объем усеченной треугольной призмы с площадью основания A и тремя высотами h 1 , h 2 и h 3 определяется по формуле
Грани
Есть два полного D 3h симметрия facetings из в треугольной призме , как с 6 равнобедренными треугольниками гранями, один сохраняя оригинальные верхние и нижние треугольники, и один оригинальные квадраты. Две нижние грани симметрии C 3v имеют один базовый треугольник, 3 боковые скрещенные квадратные грани и 3 боковые грани равнобедренного треугольника.
| Выпуклый | Грани | |||
|---|---|---|---|---|
| D 3h симметрия | C 3v симметрия | |||

|

|

|

|

|
| 2 {3} 3 {4} |
3 {4} 6 () v {} |
2 {3} 6 () v {} |
1 {3} 3 t ‘{2} 6 () v {} |
1 {3} 3 t ‘{2} 3 () v {} |
Связанные многогранники и мозаики

| Имя призмы | Дигональная призма | (Тригональная) Треугольная призма |
(Тетрагональная) Квадратная призма |
Пятиугольная призма | Шестиугольная призма | Семиугольная призма | Восьмиугольная призма | Эннеагональная призма | Десятиугольная призма | Шестиугольная призма | Додекагональная призма | … | Апейрогональная призма |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника |
|
|
|
|
|
|
|
|
|
|
|
… | |
| Сферическое мозаичное изображение |
|
|
|
|
|
|
|
|
Плоское мозаичное изображение |
|
|||
| Конфигурация вершины. | 2.4.4 | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | … | ∞.4.4 |
| Диаграмма Кокстера |
|
|
|
|
|
|
|
|
|
|
|
… |
|
| п | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Имя | {2} || т {2} | {3} || т {3} | {4} || т {4} | {5} || т {5} | {6} || т {6} |
| короткий код | 2c | 3c | 4c | 5c | 6c |
| Купол |
 Дигональный купол |
 Треугольный купол |
 Квадратный купол |
 Пятиугольный купол |
 Шестиугольный купол (плоский) |
| Связанные однородные многогранники |
Треугольная призма |
Cubocta- гранник |
Rhombi- cubocta- гранник |
Rhomb- icosidodeca- гранник |
Rhombi- trihexagonal плиточные |
Мутации симметрии
Этот многогранник топологически связан как часть последовательности однородных усеченных многогранников с конфигурациями вершин (3.2n.2n) и симметрией [n, 3] группы Кокстера .
* n 32 изменение симметрии усеченных мозаик: t { n , 3}
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия * n 32 [n, 3] |
Сферический | Евклид. | Компактная гиперболия. | Paraco. | Некомпактный гиперболический | ||||||
| * 232 [2,3] |
* 332 [3,3] |
* 432 [4,3] |
* 532 [5,3] |
* 632 [6,3] |
* 732 [7,3] |
* 832 [8,3] … |
* ∞32 [∞, 3] |
[12i, 3] | [9i, 3] | [6i, 3] | |
| Усеченные фигуры |
|

|

|

|

|

|

|

|

|

|

|
| Условное обозначение | т {2,3} | т {3,3} | т {4,3} | т {5,3} | т {6,3} | т {7,3} | т {8,3} | т {∞, 3} | т {12i, 3} | т {9i, 3} | т {6i, 3} |
Фигуры Триаки |

|
|

|

|

|

|

|

|
|||
| Конфиг. | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ |
Этот многогранник топологически связан как часть последовательности скошенных многогранников с фигурой вершины (3.4.n.4) и продолжается как мозаики гиперболической плоскости . Эти вершинно-транзитивные фигуры обладают (* n32) отражательной симметрией .
Этот многогранник топологически связан как часть последовательности скошенных многогранников с фигурой вершины (3.4.n.4) и продолжается как мозаики гиперболической плоскости . Эти вершинно-транзитивные фигуры обладают (* n32) отражательной симметрией .
| * n 32 изменение симметрии расширенных мозаик: 3.4. п. 4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия * n 32 [n, 3] |
Сферический | Евклид. | Компактная гиперболия. | Paracomp. | ||||
| * 232 [2,3] |
* 332 [3,3] |
* 432 [4,3] |
* 532 [5,3] |
* 632 [6,3] |
* 732 [7,3] |
* 832 [8,3] … |
* ∞32 [∞, 3] |
|
| Фигура |
|

|

|

|

|

|

|

|
| Конфиг. | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Соединения
Есть 4 однородных соединения треугольных призм:
- Соединение четырех треугольных призм , соединение восьми треугольных призм , соединение десяти треугольных призм , соединение двадцати треугольных призм .
Соты
Есть 9 однородных сот, которые включают ячейки треугольной призмы:
- Gyroelongated чередовались кубические сотни , удлиненной чередовались кубические соты , вращались треугольные призматические сотни , пренебрежительны квадратные призматические соты , треугольные призматические соты , треугольный-гексагональной призматические соты , усеченный гексагональный призматические сотни , rhombitriangular-гексагональная призматические сотни , вздернутые треугольные гексагональной призматические сотни , удлиненный треугольными призматические соты
Треугольная призма является первой в размерном ряду полуправильных многогранников . Каждый прогрессивный равномерный многогранник строится вершинной фигурой предыдущего многогранника. Торольд Госсет определил эту серию в 1900 году как содержащую все фасеты правильных многогранников , содержащие все симплексы и ортоплексы ( равносторонние треугольники и квадраты в случае треугольной призмы). В обозначениях Кокстера треугольной призме присвоен символ −1 21 .
| k 21 фигурка в n-мерном формате | ||||||||
|---|---|---|---|---|---|---|---|---|
| Космос | Конечный | Евклидово | Гиперболический | |||||
| E n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
Группа Коксетера |
Е 3 = А 2 А 1 | E 4 = A 4 | E 5 = D 5 | E 6 | E 7 | E 8 | E 9 = = E 8 +
|
E 10 = = E 8 ++
|
|
Диаграмма Кокстера |
|
|
|
|
|
|
|
|
| Симметрия | [3 −1,2,1 ] | [3 0,2,1 ] | [3 1,2,1 ] | [3 2,2,1 ] | [3 3,2,1 ] | [3 4,2,1 ] | [3 5,2,1 ] | [3 6,2,1 ] |
| порядок | 12 | 120 | 1,920 | 51 840 | 2 903 040 | 696 729 600 | ∞ | |
| График |

|

|

|

|

|

|
– | – |
| Имя | −1 21 | 0 21 | 1 21 | 2 21 | 3 21 | 4 21 | 5 21 | 6 21 |
Четырехмерное пространство
Треугольная призма существует в виде ячеек ряда четырехмерных однородных 4-многогранников , в том числе:
| Четырехмерные многогранники с треугольными призмами | |||||||
|---|---|---|---|---|---|---|---|
|
Тетраэдрическая призма |
Восьмигранная призма |
Кубооктаэдрическая призма |
Икосаэдрическая призма |
Икозододекаэдрическая призма |
Усеченная додекаэдрическая призма |
||

|

|

|

|

|

|
||
|
Ромбо-икосододекаэдрическая призма |
Ромби-кубооктаэдрическая призма |
Усеченная кубическая призма |
Плоская додекаэдрическая призма |
n-угольная антипризматическая призма |
|||

|

|

|

|

|
|||
|
Собранный 5-элементный |
Усеченный 5-элементный |
Ранцинированный 5-клеточный |
Усеченный 5-элементный |
Кантеллированный тессеракт |
Усеченный тессеракт |
Бегущий тессеракт |
Выполнить усеченный тессеракт |

|

|

|

|

|

|

|

|
|
Собранный 24-элементный |
Cantitruncated 24-элементный |
Ранцинированный 24-элементный |
Runcitruncated 24-элементный |
Собранный 120-элементный |
Усеченный 120-элементный |
Ранцинированный 120-клеточный |
Усеченный 120-элементный |

|

|

|

|

|

|

|

|
Смотрите также
- Клин (геометрия)
использованная литература
- Вайсштейн, Эрик В. «Треугольная призма» . MathWorld .
- Интерактивный многогранник: треугольная призма
- Площадь и объем треугольной призмы
Как рассчитать объем усеченной пирамиды
На данной странице калькулятор поможет рассчитать объем усеченной пирамиды онлайн. Для расчета задайте площадь верхнего и нижнего основания и высоту. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Усеченная пирамида — многогранник, образованный пирамидой и её сечением, параллельным основанию.
Через основания и высоту
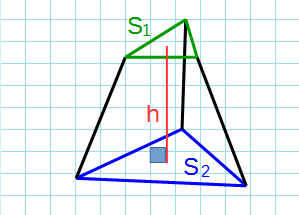
Формула объема усеченной пирамиды через высоту и площадь основания:
S1 – площадь верхнего основания; S2 – площадь нижнего основания; h – высота усеченной пирамиды.




