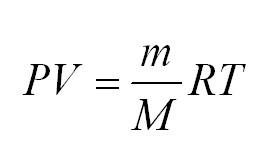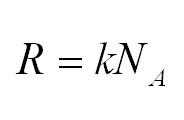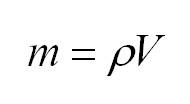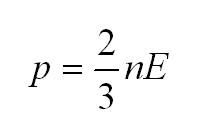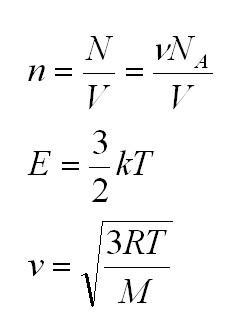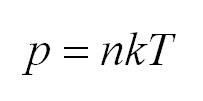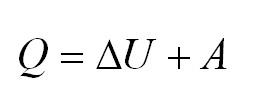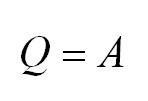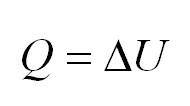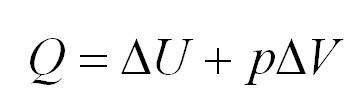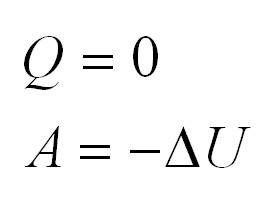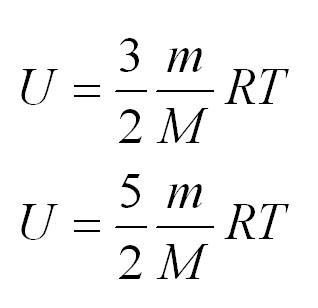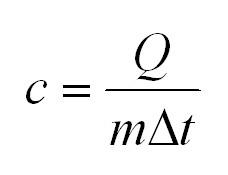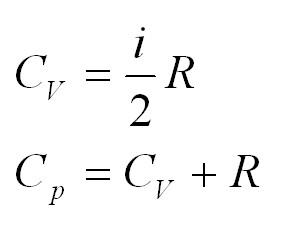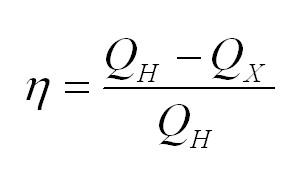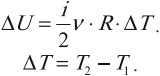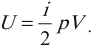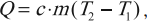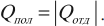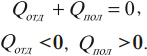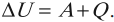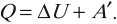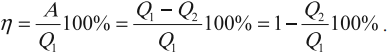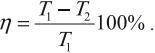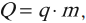Как найти объем в физике термодинамика

Основные формулы термодинамики и молекулярной физики, которые вам пригодятся. Еще один отличный день для практических занятий по физике. Сегодня мы соберем вместе формулы, которые чаще всего используются при решении задач в термодинамике и молекулярной физике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Итак, поехали. Попытаемся изложить законы и формулы термодинамики кратко.

Идеальный газ

Идеальный газ – это идеализация, как и материальная точка. Молекулы такого газа являются материальными точками, а соударения молекул – абсолютно упругие. Взаимодействием же молекул на расстоянии пренебрегаем. В задачах по термодинамике реальные газы часто принимаются за идеальные. Так гораздо легче жить, и не нужно иметь дела с массой новых членов в уравнениях.

Итак, что происходит с молекулами идеального газа? Да, они движутся! И резонно спросить, с какой скоростью? Конечно, помимо скорости молекул нас интересует еще и общее состояние нашего газа. Какое давление P он оказывает на стенки сосуда, какой объем V занимает, какая у него температура T.

Для того, чтобы узнать все это, есть уравнение состояния идеального газа, или уравнение Клапейрона-Менделеева

Здесь m – масса газа, M – его молекулярная масса (находим по таблице Менделеева), R – универсальная газовая постоянная, равная 8,3144598(48) Дж/(моль*кг).

Универсальная газовая постоянная может быть выражена через другие константы (постоянная Больцмана и число Авогадро)

Массу, в свою очередь, можно вычислить, как произведение плотности и объема.

Основное уравнение молекулярно-кинетической теории (МКТ)

Как мы уже говорили, молекулы газа движутся, причем, чем выше температура – тем быстрее. Существует связь между давлением газа и средней кинетической энергией E его частиц. Эта связь называется основным уравнением молекулярно-кинетической теории и имеет вид:

Здесь n – концентрация молекул (отношение их количества к объему), E – средняя кинетическая энергия. Найти их, а также среднюю квадратичную скорость молекул можно, соответственно, по формулам:

Подставим энергию в первое уравнение, и получим еще один вид основного уравнения МКТ

Первое начало термодинамики. Формулы для изопроцессов

Напомним Вам, что первый закон термодинамики гласит: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа U и на совершение газом работы A. Формула первого закона термодинамики записывается так:

Как известно, с газом что-то происходит, мы можем сжать его, можем нагреть. В данном случае нас интересуют такие процессы, которые протекают при одном постоянном параметре. Рассмотрим, как выглядит первое начало термодинамики в каждом из них.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы. 

Изотермический процесс протекает при постоянной температуре. Тут работает закон Бойля-Мариотта: в изотермическом процессе давление газа обратно пропорционально его объёму. В изотермическом процессе:

Изохорный процесс протекает при постоянном объеме. Для этого процесса характерен закон Шарля: При постоянном объеме давление прямо пропорционально температуре. В изохорном процессе все тепло, подведенное к газу, идет на изменение его внутренней энергии.

Изобарный процесс идет при постоянном давлении. Закон Гей-Люссака гласит, что при постоянном давлении газа его объём прямо пропорционален температуре. При изобарном процессе тепло идет как на изменение внутренней энергии, так и на совершение газом работы.

Адиабатный процесс. Адиабатный процесс – это такой процесс, который проходит без теплообмена с окружающей средой. Это значит, что формула первого закона термодинамики для адиабатного процесса выглядит так:

Внутренняя энергия одноатомного и двухатомного идеального газа

Теплоемкость

Удельная теплоемкость равна количеству теплоты, которое необходимо для нагревания одного килограмма вещества на один градус Цельсия.

Помимо удельной теплоемкости, есть молярная теплоемкость (количество теплоты, необходимое для нагревания одного моля вещества на один градус) при постоянном объеме, и молярная теплоемкость при постоянном давлении. В формулах ниже, i – число степеней свободы молекул газа. Для одноатомного газа i=3, для двухатомного – 5.

Тепловые машины. Формула КПД в термодинамике

Тепловая машина, в простейшем случае, состоит из нагревателя, холодильника и рабочего тела. Нагреватель сообщает тепло рабочему телу, оно совершает работу, затем охлаждается холодильником, и все повторяется вновь. Типичным примером тепловой машины является двигатель внутреннего сгорания.

Коэффициент полезного действия тепловой машины вычисляется по формуле

Вот мы и собрали основные формулы термодинамики, которые пригодятся в решении задач. Конечно, это не все все формулы из темы термодинамика, но их знание действительно может сослужить хорошую службу. А если возникнут вопросы  – помните о студенческом сервисе, специалисты которого готовы в любой момент прийти на выручку.

From Wikipedia, the free encyclopedia

For the general geometric concept, see Volume.

Volume (thermodynamics)
Common symbols	V
SI unit	m3

In thermodynamics, the volume of a system is an important extensive parameter for describing its thermodynamic state. The specific volume, an intensive property, is the system’s volume per unit of mass. Volume is a function of state and is interdependent with other thermodynamic properties such as pressure and temperature. For example, volume is related to the pressure and temperature of an ideal gas by the ideal gas law.

The physical volume of a system may or may not coincide with a control volume used to analyze the system.

Overview[edit]

The volume of a thermodynamic system typically refers to the volume of the working fluid, such as, for example, the fluid within a piston. Changes to this volume may be made through an application of work, or may be used to produce work. An isochoric process however operates at a constant-volume, thus no work can be produced. Many other thermodynamic processes will result in a change in volume. A polytropic process, in particular, causes changes to the system so that the quantity is constant (where is pressure, is volume, and is the polytropic index, a constant). Note that for specific polytropic indexes, a polytropic process will be equivalent to a constant-property process. For instance, for very large values of approaching infinity, the process becomes constant-volume.

Gases are compressible, thus their volumes (and specific volumes) may be subject to change during thermodynamic processes. Liquids, however, are nearly incompressible, thus their volumes can be often taken as constant. In general, compressibility is defined as the relative volume change of a fluid or solid as a response to a pressure, and may be determined for substances in any phase. Similarly, thermal expansion is the tendency of matter to change in volume in response to a change in temperature.

Many thermodynamic cycles are made up of varying processes, some which maintain a constant volume and some which do not. A vapor-compression refrigeration cycle, for example, follows a sequence where the refrigerant fluid transitions between the liquid and vapor states of matter.

Typical units for volume are (cubic meters), (liters), and (cubic feet).

Heat and work[edit]

Mechanical work performed on a working fluid causes a change in the mechanical constraints of the system; in other words, for work to occur, the volume must be altered. Hence, volume is an important parameter in characterizing many thermodynamic processes where an exchange of energy in the form of work is involved.

Volume is one of a pair of conjugate variables, the other being pressure. As with all conjugate pairs, the product is a form of energy. The product is the energy lost to a system due to mechanical work. This product is one term which makes up enthalpy :

where is the internal energy of the system.

The second law of thermodynamics describes constraints on the amount of useful work which can be extracted from a thermodynamic system. In thermodynamic systems where the temperature and volume are held constant, the measure of “useful” work attainable is the Helmholtz free energy; and in systems where the volume is not held constant, the measure of useful work attainable is the Gibbs free energy.

Similarly, the appropriate value of heat capacity to use in a given process depends on whether the process produces a change in volume. The heat capacity is a function of the amount of heat added to a system. In the case of a constant-volume process, all the heat affects the internal energy of the system (i.e., there is no pV-work, and all the heat affects the temperature). However, in a process without a constant volume, the heat addition affects both the internal energy and the work (i.e., the enthalpy); thus the temperature changes by a different amount than in the constant-volume case and a different heat capacity value is required.

Specific volume[edit]

Specific volume () is the volume occupied by a unit of mass of a material.^[1] In many cases, the specific volume is a useful quantity to determine because, as an intensive property, it can be used to determine the complete state of a system in conjunction with another independent intensive variable. The specific volume also allows systems to be studied without reference to an exact operating volume, which may not be known (nor significant) at some stages of analysis.

The specific volume of a substance is equal to the reciprocal of its mass density. Specific volume may be expressed in , , , or .

where, is the volume, is the mass and is the density of the material.

For an ideal gas,

where, is the specific gas constant, is the temperature and is the pressure of the gas.

Specific volume may also refer to molar volume.

Gas volume[edit]

Dependence on pressure and temperature[edit]

The volume of gas increases proportionally to absolute temperature and decreases inversely proportionally to pressure, approximately according to the ideal gas law:

where:

• p is the pressure
• V is the volume
• n is the amount of substance of gas (moles)
• R is the gas constant, 8.314 J·K⁻¹mol⁻¹
• T is the absolute temperature

To simplify, a volume of gas may be expressed as the volume it would have in standard conditions for temperature and pressure, which are 0 °C (32 °F) and 100 kPa.^[2]

Humidity exclusion[edit]

In contrast to other gas components, water content in air, or humidity, to a higher degree depends on vaporization and condensation from or into water, which, in turn, mainly depends on temperature. Therefore, when applying more pressure to a gas saturated with water, all components will initially decrease in volume approximately according to the ideal gas law. However, some of the water will condense until returning to almost the same humidity as before, giving the resulting total volume deviating from what the ideal gas law predicted. Conversely, decreasing temperature would also make some water condense, again making the final volume deviating from predicted by the ideal gas law.

Therefore, gas volume may alternatively be expressed excluding the humidity content: V_d (volume dry). This fraction more accurately follows the ideal gas law. On the contrary, V_s (volume saturated) is the volume a gas mixture would have if humidity was added to it until saturation (or 100% relative humidity).

General conversion[edit]

To compare gas volume between two conditions of different temperature or pressure (1 and 2), assuming nR are the same, the following equation uses humidity exclusion in addition to the ideal gas law:

Where, in addition to terms used in the ideal gas law:

• p_w is the partial pressure of gaseous water during condition 1 and 2, respectively

For example, calculating how much 1 liter of air (a) at 0 °C, 100 kPa, p_w = 0 kPa (known as STPD, see below) would fill when breathed into the lungs where it is mixed with water vapor (l), where it quickly becomes 37 °C (99 °F), 100 kPa, p_w = 6.2 kPa (BTPS):

Common conditions[edit]

Some common expressions of gas volume with defined or variable temperature, pressure and humidity inclusion are:

• ATPS: Ambient temperature (variable) and pressure (variable), saturated (humidity depends on temperature)
• ATPD: Ambient temperature (variable) and pressure (variable), dry (no humidity)
• BTPS: Body temperature (37 °C or 310 K) and pressure (generally same as ambient), saturated (47 mmHg or 6.2 kPa)
• STPD: Standard temperature (0 °C or 273 K) and pressure (760 mmHg (101.33 kPa) or 100 kPa (750.06 mmHg)), dry (no humidity)

Conversion factors[edit]

The following conversion factors can be used to convert between expressions for volume of a gas:^[3]

To convert from	To	Multiply by
ATPS	STPD	[(PA – Pwater S) / PS] * [TS / TA]
BTPS	[(PA – Pwater S) / (PA – Pwater B)] * [TB/TA]
ATPD	(PA – Pwater S) / PA
ATPD	STPD	(PA / PS) * (TS / TA)
BTPS	[PA / (PA – Pwater B)] * (TB / TA)
ATPS	PA / (PA – Pwater S)
BTPS	STPD	[(PA – Pwater B) / PS] * [TS / TB]
ATPS	[(PA – Pwater B) / (PA – Pwater S)] * [TA / TB]
ATPD	[(PA – Pwater B) / PA] * [TA / TB]
STPD	BTPS	[PS / (PA – Pwater B)] * [TB / TS]
ATPS	[PS / (PA – Pwater S)] * [TA / TS]
ATPD	[PS / PA] * [TA / TS]
Legend: PA = Ambient pressure PS = Standard pressure (100 kPa or 750 mmHg) Pwater S = Partial pressure of water in saturated air (that is, at 100% relative humidity; in this case the partial pressure is equal to the vapour pressure, which can be determined as a function of ambient temperature) Pwater B = Partial pressure of water in saturated air in 37 °C = 47 mmHg TS = Standard temperature in kelvins (K) = 273 K TA = Ambient temperature in kelvins = 273 + t (where t is ambient temperature in °C) TB = Body temperature in kelvins = 310 K

Partial volume[edit]

The partial volume of a particular gas is the volume which the gas would have if it alone occupied the volume, with unchanged pressure and temperature, and is useful in gas mixtures, e.g. air, to focus on one particular gas component, e.g. oxygen.

It can be approximated both from partial pressure and molar fraction:^[4]

• V_X is the partial volume of any individual gas component (X)
• V_tot is the total volume in gas mixture
• P_X is the partial pressure of gas X
• P_tot is the total pressure in gas mixture
• n_X is the amount of substance of a gas (X)
• n_tot is the total amount of substance in gas mixture

See also[edit]

• Volumetric flow rate

References[edit]

Физическая дисциплина «Термодинамика», имеющая дословный перевод с греческого как θέρμη — «тепло», δύναμις — «сила», занимается изучением общих характеристик макросистем и обращения энергии внутри них. Эту науку относят к феноменологическому типу, хотя опирается она на факты, полученные опытным путем.

Термодинамическая система, рассматриваемая в данном ракурсе, имеет конкретные характеристики, не применимые к единичным атомам и молекулам. К ним относят температуру, энергию, объем, концентрацию растворов, давление.

Определение таких параметров происходит по формулам термодинамики.

Основные формулы термодинамики

Особенностью термодинамики является то, что ее постулаты не касаются взаимодействия отдельных единиц (атомов, молекул), как в молекулярной физике. Предметом изучения предстают общие взаимопревращения энергии, образование теплоты, теплопередача и совершение работы.

Исходя из этого, выделяют основные формулы термодинамики, к которым относятся:

1. Уравнение Менделеева-Клайперона: (PV=(m/M)*RT). Его смысл — в изменениях трех входящих величин, которые направлены на характеристику состояния идеального газа.
2. Количество вещества, обозначаемое буквой (ν). (nu=N/NA=m/mu)

   Величина, выражающая, сколько одинаковых структурных компонентов (единиц) находится в веществе.

3. Закон Дальтона: давление смеси газов на стенку сосуда равно сумме давлений каждого входящего в смесь элемента: (p=p1+p2+…pn.)
4. Главное уравнение МКТ (молекулярно-кинетической теории): (p=2n/3<varepsilon>n=N/V). Выражает математическое соотношение таких параметров, как давление газа и микропараметров: массы молекул, их скорости движения, концентрации.
5. Средняя кинетическая энергия поступательного движения молекулы газа. Для обозначения применяется (E_k),  выражается через формулу: (E_k=E_{моля}/NA=3/2ast RT/NA). Ее мерой является абсолютная температура идеального газа, поскольку потенциальная энергия (вследствие взаимодействия молекул друг с другом) равна нулю. Зная, что R/N_A=k, получается формула: (E_k=3/2ast kT).
6. Давление идеального газа прямо пропорционально концентрации и его температуре: (P=nkT.)
7. Скорость молекул определяется по формулам:
   (V=surd(2kT/m_o)=surd(2RT/mu)) — наиболее вероятная;
   (<V>=surd(8kT/pi m_o)=surd(8RT/pimu)) — среднеарифметическая;
   (<Vкв>surd(3kT/m_o)=surd(3RT/mu)) — средняя квадратичная.
8. Сумма кинетических энергий всех молекул определяет внутреннюю энергию всего идеального газа. Математически выражение выглядит так: (U=i/2ast(m/mu)ast RT.)
9. Формула для определения работы, которую совершает идеальный газ при расширении:( A=P(V_2-V_1).)
10. Формула первого закона термодинамики: (Q=Delta U+A.)
11. Для определения удельной теплоемкости вещества применяется математическое выражение: (С=Delta Q/mdT.)
12. Кроме удельной теплоемкости, существует понятие молярной теплоемкости. Для ее определения применяется формула: (C=cmu). Для изохорного процесса правильная формула принимает вид: (C_v=1/2ast R), для изобарного: (C_p=((i+2)/2)ast R).

Первое начало термодинамики

Согласно первому закону термодинамики, (Q) (количество внутренней теплоты), которое получил газ извне, расходуется на совершение работы (А) и изменение внутренней энергии (U). Формула закона: (Q=Delta U+A).

На практике газ может быть нагрет либо охлажден. Однако в данном случае рассматривается изотермический процесс, в котором один из характеризующих параметров остается неизменным.

Если процесс изотермичен, в химии включается закон Бойля-Мариота. В нем говорится, что давление газа соотносится к изначальному объему, при стабильной температуре, обратно пропорционально.

(Q=A)

Когда процесс происходит при неизменном объеме, говорят об изохорности. Здесь вступает в действие закон Шарля. В обозначенных условиях то тепло, которое поступило к газу, расходуется на изменение внутренней энергии. Другими словами, (P) пропорционально (T).

(Q=Delta U)

Протекание процессов в идеальном газе при неизменном давлении носит характер изобарного. Здесь действует закон Гей-Люссака, который выражается уравнением:

(Q=Delta U=pDelta V)

Полная формулировка закона гласит: полученное тепло при изобарном процессе расходуется на совершение работы газом, а также изменяет его внутреннюю энергию.

Часть процессов происходят изолированно от внешней среды. Газ не получает дополнительной энергии. Такая ситуация носит название адиабатной и математически записывается: (Q=0). Работа (А) в таком случае выражается: (A=-Delta U.)

Уравнение идеального газа в термодинамике

Молекулы идеального газа постоянно движутся. От того насколько велика скорость их движения, зависит общее состояние газа, а также величина его воздействия, например, на стенки сосуда. Поэтому одним из основных уравнений термодинамики является Клайперона-Менделеева:

(PV=(m/M)ast RT)

В уравнении (m) — единица массы газа, (M) — его молекулярная масса, (R) — универсальная величина, называемая газовой постоянной. Ее значение = 8,3144598. Измеряется в Дж/(моль*кг).

В основе термодинамики лежат и другие газовые постоянные, например, число Авогадро, постоянная Больцмана. Таким образом, (R=kNA.)

Из уравнения Клайперона-Менделеева можно также вычислить массу. Она будет равна произведению плотности на объем: (m=rho V).

Основное уравнение молекулярно-кинетической теории (МКТ)

Решение части задач зависит от знания особенностей взаимосвязи между давлением газа и характеристикой кинетической энергии его молекул. Математическое выражение такой зависимости носит название основного уравнения МКТ:

(p=2/3ast nE)

В данном выражении кинетическая энергия обозначена буквой (Е), а концентрация молекул — (n). Каждую из этих величин физики можно найти исходя из соответствующих формул, после чего уравнение для молекулярно-кинетической теории (МКТ) приобретает вид:

(p=nkT)

Формула теплоемкости и главная формула КПД в термодинамике

Когда теплообмен проявляется передачей телу определенного количества теплоты, его энергия, как и температура, меняются.

То количество теплоты, обозначаемое (Q), которое понадобится для того, чтобы 1 кг определенного вещества нагреется на 1 К, носит определение теплоемкости вещества и обозначается с.

Математическое выражение относительно переданного количества теплоты выглядит формулой:

(Q=cm(t_2-t_1)=cmDelta t)

Измеряется величина в Дж/(кг∙К).

При t2⟩t1, количество теплоты со знаком плюс, следовательно, вещество нагревается. Если наоборот, то Q — со знаком минус, и вещество остывает.

В физике, характеризуя свойства вещества, говорят о его теплоемкости. Это имеет значение, например, при выборе стройматериалов или сырья для изготовления нагревательных приборов. Теплоемкость равна произведению массы на удельную теплоемкость данного тела:

(C=cm)

Учитывая, что в величине теплоемкости уже отражена масса, то сокращенная формула для определения (Q) выглядит так:

 (Q=C(t_2-t_1))

С другой стороны, то количество теплоты, которое отдает источник, можно высчитать по формуле: 

(Q=Pt.)

В выражении буквой (P) обозначается мощность нагревателя, а (t) — время их контакта.

Конструкция, состоящая из нагревателя, тела-реципиента теплоты и охладителя, носит название тепловой машины. В качестве примера рассматривается двигатель внутреннего сгорания. Как и любой механизм, она имеет такую характеристику, как КПД — коэффициент полезного действия. Для его расчета применяется формула:

(eta=(Q_н-Q_x)/Q_н)

Внутренняя энергия одноатомного и двухатомного идеального газа

Характерной особенностью идеального газа является отсутствие у его составляющих частей потенциальной энергии. Вся внутренняя энергия — это сумма кинетических энергий всех молекул. Она является величиной, прямо пропорциональной температуре идеального газа:

(mw2/2=alpha T)

В этом уравнении:

(alpha T=3Rmu/2Nmu)

Исходя из приведенных формул, величина кинетической энергии поступательного движения идеального газа должна определяться исходя из выражения:

(mv2/2=(3Rmu/2Nmu)ast T)

Поступательное движение характеризуется тремя степенями свободы. На каждую из них приходится одна треть общей кинетической энергии.

Двух- и более атомные молекулы газа характеризуются степенями свободы, касающимися вращательного движения.

Если обозначить число молекул в одном киломоле за (Nμ), то внутренняя энергия идеального газа будет измеряться по формуле:

(Umu=1/2(Rmu Ti))

В формуле (i) — число степеней свобод.

Если газ одноатомный, (i=3), двуатомный — 5, трех- и более — 6.

Задачи на термодинамику характеризуют распространенные физические процессы, поэтому часть включаются в программы экзаменов. Если для их решения не хватает времени, можно обратиться за помощью в Феникс.Хелп. На профильном сайте вам помогут справиться с любой, даже запутанной задачей, экономя ваши время и силы.

Термодинамика

Термодинамика – это раздел физики, изучающий тепловые свойства макроскопических тел и систем тел, находящихся в состоянии теплового равновесия, на основе закона сохранения энергии, без учета внутреннего строения тел, составляющих систему.

Термодинамика не рассматривает микроскопические величины – размеры атомов и молекул, их массы и количество.

Законы термодинамики устанавливают связи между непосредственно наблюдаемыми физическими величинами, характеризующими состояние системы, такими как давление ​( p )​, объем ​( V )​, температура ​( T )​.

Внутренняя энергия

Внутренняя энергия – это физическая величина, равная сумме кинетической энергии теплового движения частиц тела и потенциальной энергии их взаимодействия друг с другом.

Обозначение – ​( U )​, в СИ единица измерения – Джоуль (Дж).

В термодинамике внутренняя энергия зависит от температуры и объема тела.

Внутренняя энергия тел зависит от их температуры, массы и агрегатного состояния. С ростом температуры внутренняя энергия увеличивается. Наибольшая внутренняя энергия у вещества в газообразном состоянии, наименьшая – в твердом.

Внутренняя энергия идеального газа представляет собой только кинетическую энергию теплового движения его частиц; потенциальная энергия взаимодействия частиц равна нулю.

Внутренняя энергия идеального газа прямо пропорциональна его температуре, а от объема не зависит (молекулы идеального газа не взаимодействуют друг с другом):

где ​( i )​ – коэффициент, равный числу степеней свободы молекулы, ​( nu )​ – количество вещества, ​( R )​ – универсальная газовая постоянная, ​( T )​ – абсолютная температура.

Число степеней свободы равно числу возможных движений частицы.

Важно!
Для одноатомных газов коэффициент ​( i )​ = 3, для двухатомных газов ​( i )​ = 5.

На практике часто важно уметь находить изменение внутренней энергии:

При решении задач можно записать формулу для вычисления внутренней энергии, используя уравнение Менделеева–Клапейрона:

где ​( p )​ – давление, ​( V )​ – объем газа.

Внутренняя энергия реальных газов зависит как от температуры, так и от объема.

Изменить внутреннюю энергию можно за счет изменения температуры (при теплопередаче) и за счет изменения давления и объема (при совершении работы).

Тепловое равновесие

Тепловое равновесие – это состояние системы, при котором все ее макроскопические параметры остаются неизменными сколь угодно долго.

Величины, характеризующие состояние макроскопических тел без учета их молекулярного строения, называются макроскопическими параметрами. К ним относятся давление и температура, объем, масса, концентрация отдельных компонентов смеси газа и др. В состоянии теплового равновесия отсутствует теплообмен с окружающими телами, отсутствуют переходы вещества из одного агрегатного состояния в другое, не меняются температура, давление, объем.

Любая термодинамическая система переходит самопроизвольно в состояние теплового равновесия. Каждому состоянию теплового равновесия, в которых может находиться термодинамическая система, соответствует определенная температура.

Важно!
В состоянии теплового равновесия объем, давление могут быть различными в разных частях термодинамической системы, и только температура во всех частях термодинамической системы, находящейся в состоянии теплового равновесия, является одинаковой. Микроскопические процессы внутри тела не прекращаются и при тепловом равновесии: меняются положения молекул, их скорости при столкновениях.

Теплопередача

Теплопередача – процесс изменения внутренней энергии тела без совершения работы.

Существуют три вида теплопередачи: теплопроводность, конвекция и излучение (лучистый теплообмен). Теплопередача происходит между телами, имеющими разную температуру. Тепло передается от тела с более высокой температурой к телу с более низкой температурой.

Теплопроводность – это процесс переноса энергии от более нагретых тел (частей тела) к менее нагретым в результате движения и взаимодействия частиц тела. Высокую теплопроводность имеют металлы – так, лучшие проводники тепла – медь, золото, серебро. Теплопроводность жидкостей меньше, а газы являются плохими проводниками тепла. Пористые тела плохо проводят тепло, так как в порах содержится воздух. Вещества с низкой теплопроводностью используют в качестве теплоизоляторов. Теплопроводность невозможна в вакууме. При теплопроводности не происходит переноса вещества.

Явление теплопроводности газов аналогично явлению диффузии. Быстрые молекулы из слоя с более высокой температурой перемещаются в более холодный слой, а молекулы из холодного слоя перемещаются в более нагретый. За счет этого средняя кинетическая энергия молекул более теплого слоя уменьшается, и его температура становится ниже.

В жидкостях и твердых телах при повышении температуры какого-либо участка твердого тела или жидкости его частицы начинают колебаться сильнее. Соударяясь с соседними частицами, где температура ниже, эти частицы передают им часть своей энергии, и температура этого участка возрастает.

Конвекция – перенос энергии потоками жидкости или газа.

Объяснить механизм конвекции можно на основе теплового расширения тел и закона Архимеда. При нагревании объем жидкости увеличивается, а плотность уменьшается. Нагретый слой под действием силы Архимеда поднимается вверх, а холодный опускается вниз. Это естественная конвекция. Она возникает при неравномерном нагревании жидкости или газа снизу в поле тяготения.

При вынужденной конвекции перемещение вещества происходит под действием насосов, лопастей вентилятора. Такая конвекция применяется в состоянии невесомости. Интенсивность конвекции зависит от разности температур слоев среды и агрегатного состояния вещества. Конвекционные потоки поднимаются вверх. При конвекции происходит перенос вещества.

В твердых телах конвекция невозможна, так как частицы не могут из-за сильного взаимодействия покидать свои места. В вакууме конвекция также невозможна.

Примером конвективных потоков в природе являются ветры (бризы дневной и ночной, муссоны).

Излучение (лучистый теплообмен) – перенос энергии электромагнитными волнами. Перенос тепла излучением возможен в вакууме. Источником излучения является любое тело, температура которого отлична от нуля К. При поглощении энергия теплового излучения переходит во внутреннюю энергию. Темные тела быстрее нагреваются излучением, чем тела с блестящей поверхностью, но и остывают быстрее. Мощность излучения зависит от температуры тела. С увеличением температуры тела энергия излучения увеличивается. Чем больше площадь поверхности тела, тем интенсивнее излучение.

Количество теплоты. Удельная теплоемкость вещества

Количество теплоты – это скалярная физическая величина, равная энергии, которую тело получило или отдало при теплопередаче.

Обозначение – ​( Q )​, в СИ единица измерения – Дж.

Удельная теплоемкость – это скалярная физическая величина, численно равная количеству теплоты, которое тело массой 1 кг получает или отдает при изменении его температуры на 1 К.

Обозначение – ​( c )​, в СИ единица измерения – Дж/(кг·К).

Удельная теплоемкость определяется не только свойствами вещества, но и тем, в каком процессе осуществляется теплопередача. Поэтому выделяют удельную теплоемкость газа при постоянном давлении – ​( c_P )​ и удельную теплоемкость газа при постоянном объеме – ​( c_V )​. Для нагревания газа на 1 К при постоянном давлении требуется большее количество теплоты, чем при постоянном объеме – ​( c_P > c_V )​.

Формула для вычисления количества теплоты, которое получает тело при нагревании или отдает при охлаждении:

где ​( m )​ – масса тела, ​( c )​ – удельная теплоемкость, ​( T_2 )​ – конечная температура тела, ​( T_1 )​ – начальная температура тела.

Важно!
При решении задач на расчет количества теплоты при нагревании или охлаждении можно не переводить температуру в кельвины. Так как 1К=1°С, то​( Delta T=Delta t )​.

Работа в термодинамике

Работа в термодинамике равна изменению внутренней энергии тела.

Обозначение работы газа – ​( A’ )​, единица измерения в СИ – джоуль (Дж). Обозначение работы внешних сил над газом – ​( A )​.

Работа газа ​( A’ =-A )​.

Работой расширения идеального газа называют работу, которую газ совершает против внешнего давления.

Работа газа положительна при расширении и отрицательна при его сжатии. Если объем газа не изменяется (изохорный процесс), то работы газ не совершает.

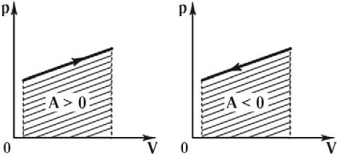
Графически работа газа может быть вычислена как площадь фигуры под графиком зависимости давления от объема в координатных осях ​( (p,V) )​, ограниченная графиком, осью ​( V )​ и перпендикулярами, проведенными из точек начального и конечного значений объема.

Формула для вычисления работы газа:

в изобарном процессе ​( A’=pcdotDelta V. )​

в изотермическом процессе ( A’=frac{m}{M}RTlnfrac{V_2}{V_1}. )​

Уравнение теплового баланса

Если система тел является теплоизолированной, то ее внутренняя энергия не будет изменяться несмотря на изменения, происходящие внутри системы. Если ​( A )​ = 0, ​( Q )​ = 0, то и ​( Delta U )​ = 0 .

При любых процессах, происходящих в теплоизолированной системе, ее внутренняя энергия не изменяется (закон сохранения внутренней энергии).

Рассмотрим теплоизолированную систему из двух тел с разными температурами. При контакте между ними будет проходить теплообмен. Тело с большей температурой будет отдавать некоторое количество теплоты, а тело с меньшей температурой – получать, пока температуры тел не станут равными. Так как суммарная внутренняя энергия не должна изменяться, то, на сколько уменьшится внутренняя энергия более нагретого тела, на столько должна увеличиться внутренняя энергия второго тела. Так как работа не совершается, то изменение внутренней энергии равно количеству теплоты.

Количество теплоты, отданное при теплообмене телом с большей температурой, равно по модулю количеству теплоты, полученному телом с меньшей температурой:

Другая формулировка: если тела образуют замкнутую систему и между ними происходит только теплообмен, то алгебраическая сумма отданных ​( Q_{отд} )​ и полученных ( Q_{пол} ) количеств теплоты равна нулю:

Первый закон термодинамики

Закон сохранения и превращения энергии, распространенный на тепловые явления, называется первым законом (началом) термодинамики.

Можно дать формулировку этого закона исходя из способов изменения внутренней энергии.

Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:

Если рассматривать работу самой системы над внешними телами, то закон может быть сформулирован так:

количество теплоты, переданное системе, идет на изменение ее внутренней энергии и совершение системой работы над внешними телами:

Если система изолирована и над ней не совершается работа и нет теплообмена с внешними телами, то в этом случае внутренняя энергия не изменяется. Если к системе не поступает теплота, то работа системой может совершаться только за счет уменьшения внутренней энергии. Это значит, что невозможно создать вечный двигатель – устройство, способное совершать работу без каких-либо затрат топлива.

Первый закон термодинамики для изопроцессов

Изотермический процесс: ​( Q=A’,(T=const, Delta U=0) )​
Физический смысл: все переданное газу тепло идет на совершение работы.

Изобарный процесс: ( Q=Delta U+A’ )​
Физический смысл: подводимое к газу тепло идет на увеличение его внутренней энергии и на совершение газом работы.

Изохорный процесс: ( Q=Delta U,(V=const, A’=0) )​
Физический смысл: внутренняя энергия газа увеличивается за счет подводимого тепла.

Адиабатный процесс: ​( Delta U=-A’ )​ или ​( A=Delta U,mathbf{(Q=0)} )​
Физический смысл: внутренняя энергия газа уменьшается за счет совершения газом работы. Температура газа при этом понижается.

Задачи об изменении внутренней энергии тел

Такие задачи можно разделить на группы:

• При взаимодействии тел изменяется их внутренняя энергия без совершения работы над внешней средой.
• Рассматриваются явления, связанные с превращением одного вида энергии в другой при взаимодействии двух тел. В результате происходит изменение внутренней энергии одного тела вследствие совершенной им или над ним работы.

При решении задач первой группы:

• установить, у каких тел внутренняя энергия уменьшается, а у каких – возрастает;
• составить уравнение теплового баланса ​( (Delta U=0) ), при записи которого в выражении ​( Q =cm(t_2 – t_1) )​ для изменения внутренней энергии нужно вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака;
• решить полученное уравнение относительно искомой величины;
• проверить решение.

При решении задач второй группы:

• убедиться, что в процессе взаимодействия тел теплота извне к ним не подводится, т.е. действительно ли ​( Q = 0 )​;
• установить, у какого из двух взаимодействующих тел изменяется внутренняя энергия и что является причиной этого изменения – работа, совершенная самим телом, или работа, совершенная над телом;
• записать уравнение ​( Q = Delta U + A )​ для тела, у которого изменяется внутренняя энергия, учитывая знак перед работой и КПД рассматриваемого процесса;
• если работа совершается за счет уменьшения внутренней энергии одного из тел, то ​( А= -Delta U )​, а если внутренняя энергия тела увеличивается за счет работы, совершенной над телом, то ​( A=Delta U )​;
• найти выражения для ​( Delta U )​ и ​( A )​;
• подставить в исходное уравнение вместо ( Delta U ) и ( A ) выражения для них, получить окончательное соотношение для определения искомой величины;
• решить полученное уравнение относительно искомой величины;
• проверить решение.

Второй закон термодинамики

Все процессы в природе протекают только в одном направлении. В обратном направлении самопроизвольно они протекать не могут. Необратимым называется процесс, обратный которому может протекать только как составляющая более сложного процесса.

Примеры необратимых процессов:

• переход тепла от более нагретого тела к менее нагретому телу;
• переход механической энергии во внутреннюю энергию.

Первый закон термодинамики ничего не говорит о направлении процессов в природе.

Второй закон термодинамики выражает необратимость процессов, происходящих в природе. Существует несколько его формулировок.

Второй закон термодинамики (формулировка Клаузиуса):
невозможно перевести тепло от более холодной системы к более горячей при отсутствии одновременных изменений в обеих системах или окружающих телах.

Второй закон термодинамики (формулировка Кельвина):
невозможно осуществить такой периодический процесс, единственным результатом которого было бы получение работы за счет теплоты, взятой от одного источника.

Эта формулировка говорит также и о том, что невозможно построить вечный двигатель второго рода, то есть двигатель, совершающий работу за счет охлаждения какого-либо одного тела.

Важно!
В формулировке второго закона термодинамики большое значение имеют слова «единственным результатом». Если процессы, о которых идет речь, не являются единственными, то запреты снимаются. Например, в холодильнике происходит передача тепла от более холодного тела к нагретому и при этом осуществляется компенсирующий процесс превращения механической энергии окружающих тел во внутреннюю энергию.

Второй закон термодинамики выполняется для систем с огромным числом частиц. В системах с малым количеством частиц возможны флуктуации – отклонения от равновесия.

КПД тепловой машины

Коэффициентом полезного действия (КПД) тепловой машины (двигателя) называется отношение работы ​( A )​, совершаемой двигателем за цикл, к количеству теплоты ​( Q_1 )​, полученному за цикл от нагревателя:

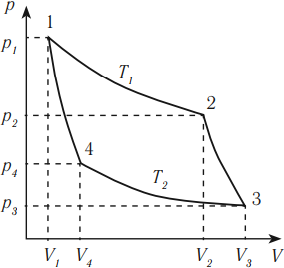
Тепловая машина с максимальным КПД была создана Карно. В машине осуществляется круговой процесс (цикл Карно), при котором после ряда преобразований система возвращается в начальное состояние.

Цикл Карно состоит из четырех стадий:

1. Изотермическое расширение (на рисунке — процесс 1–2). В начале процесса рабочее тело имеет температуру ​( T_1 )​, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передает ему количество теплоты ​( Q_1 )​. При этом объем рабочего тела увеличивается.
2. Адиабатное расширение (на рисунке — процесс 2–3). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника ​( T_2 )​.
3. Изотермическое сжатие (на рисунке — процесс 3–4). Рабочее тело, имеющее к тому времени температуру ​( T_2 )​, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты ​( Q_2 )​.
4. Адиабатное сжатие (на рисунке — процесс 4–1). Рабочее тело отсоединяется от холодильника. При этом его температура увеличивается до температуры нагревателя ​( T_1 )​.

КПД цикла Карно:

Отсюда видно, что КПД цикла Карно с идеальным газом зависит только от температуры нагревателя ​( (T_1) )​ и холодильника ( (T_2) ).

Из уравнения следуют выводы:

• для повышения КПД тепловой машины нужно увеличить температуру нагревателя и уменьшить температуру холодильника;
• КПД тепловой машины всегда меньше 1.

Цикл Карно обратим, так как все его составные части являются равновесными процессами.

КПД тепловых двигателей: двигатель внутреннего сгорания — 30%, дизельный двигатель — 40%, паровая турбина — 40%, газовая турбина — 25–30%.

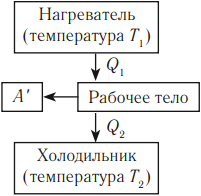
Принципы действия тепловых машин

Тепловым двигателем называют устройство, преобразующее внутреннюю энергию топлива в механическую энергию.

Основные части теплового двигателя:

• Нагреватель – тело с постоянной температурой, преобразующее внутреннюю энергию топлива в энергию газа. В каждом цикле работы двигателя нагреватель передает рабочему телу некоторое количество теплоты.
• Рабочее тело – это газ, совершающий работу при расширении.
• Холодильник – тело с постоянной температурой, которому рабочее тело передает часть тепла.

Любая тепловая машина получает от нагревателя некоторое количество теплоты ​( Q_1 )​ и передает холодильнику количество теплоты ​( Q_2 )​. Так как ​( Q_1 > Q_2 )​, то совершается работа ​( A’ = Q_1 – Q_2 )​.

Тепловой двигатель должен работать циклически, поэтому расширение рабочего тела должно сменяться его сжатием. Работа расширения газа должна быть больше работы сжатия, совершаемой внешними силами (условие совершения полезной работы). Температура газа при расширении должна быть выше, чем температура при сжатии. Тогда давление газа во всех промежуточных состояниях при сжатии будет меньше, чем при расширении.

В реальных тепловых машинах нагревателем является камера сгорания. В них рабочее тело нагревается за счет тепла, выделяющегося при сгорании топлива. Количество теплоты, выделяющееся при сгорании топлива, вычисляется по формуле:

где ​( q )​ – удельная теплота сгорания топлива, ​( m )​ – масса топлива.

Холодильником чаще всего у реальных двигателей служит атмосфера.

Виды тепловых двигателей:

• паровой двигатель;
• турбина (паровая, газовая);
• двигатель внутреннего сгорания (карбюраторный, дизельный);
• реактивный двигатель.

Тепловые двигатели широко используются на всех видах транспорта: на автомобилях – двигатели внутреннего сгорания; на железнодорожном транспорте – дизельные двигатели (на тепловозах); на водном транспорте – турбины; в авиации – турбореактивные и реактивные двигатели. На тепловых и атомных электростанциях тепловые двигатели приводят в движение роторы генераторов переменного тока.

Проблемы энергетики и охрана окружающей среды

Тепловые двигатели широко применяются на транспорте и в энергетике (тепловые и атомные электростанции). Использование тепловых двигателей сильно влияет на состояние биосферы Земли. Можно выделить следующие вредные факторы:

• при сжигании топлива используется кислород из атмосферы, что приводит к снижению содержания кислорода в воздухе;
• при сгорании топлива в атмосферу выделяется углекислый газ. Концентрация углекислого газа в атмосфере повышается. Это изменяет прозрачность атмосферы, так как молекулы углекислого газа поглощают инфракрасное излучение, что ведет к повышению температуры (парниковый эффект);
• при сжигании угля в атмосферу поступают азотные, серные соединения и соединения свинца, вредные для здоровья человека.

Решение проблемы охраны окружающей среды от вредного воздействия предприятий тепловой энергетики требует комплексного подхода. Массовыми загрязнителями при работе тепловых электростанций являются летучая зола, диоксид серы и оксиды азота. Методы сокращения выбросов зависят от свойств топлива и условия его сжижения. Предотвращение загрязнения летучей золой достигается очисткой всего объема продуктов сгорания твердого топлива в высокоэффективных золоуловителях. Сокращение выбросов оксидов азота с продуктами сгорания топлива на тепловых электростанциях, а также в парогазовых и газотурбинных установках обеспечивается, главным образом, технологией сжигания топлива. Уменьшение выброса диоксида серы может быть достигнуто различными методами облагораживания и переработки топлива вне тепловых электростанций либо непосредственно на тепловых электростанциях, а также очисткой дымовых газов.

Контроль за выбросом вредных веществ электростанций осуществляется специальными приборами.

В ряде случаев достаточно эффективным решением вопросов очистки выбросов в атмосферу остается сооружение фильтров-уловителей и дымовых труб. У дымовой трубы два назначения: первое — создавать тягу и тем самым заставлять воздух — обязательный участник процесса горения — в нужном количестве и с должной скоростью входить в топку; второе — отводить продукты горения (вредные газы и имеющиеся в дыме твердые частицы) в верхние слои атмосферы. Благодаря непрерывному турбулентному движению вредные газы и твердые частицы уносятся далеко от источника их возникновения и рассеиваются.

Для рассеивания сернистого ангидрида, содержащегося в дымовых трубах тепловых электростанций, сооружаются дымовые трубы высотой 180, 250 и 320 м. Тепловые электростанции России, работающие на твердом топливе, за год выбрасывают в отвалы около 100 млн т золы и шлаков. Зола и шлаки занимают большие площади земель, неблагоприятно влияют на окружающую среду.

Более половины всех загрязнений создает транспорт. Один из путей решения проблемы защиты окружающей среды заключается в переходе на дизельные двигатели, электродвигатели, повышение КПД.

Алгоритм решения задач раздела «Термодинамика»:

• выделить систему тел и определить ее тип (замкнутая, адиабатически замкнутая, замкнутая в механическом смысле, незамкнутая);
• выяснить, как изменяются параметры состояния ​( (p,V,T) )​ и внутренняя энергия каждого тела системы при переходе из одного состояния в другое;
• записать уравнения, связывающие параметры двух состояний системы, формулы для расчета изменения внутренней энергии каждого тела системы при переходе из одного состояния в другое;
• определить изменение механической энергии системы и работу внешних сил по изменению ее объема;
• записать формулу первого закона термодинамики или закона сохранения и превращения энергии;
• решить систему уравнений относительно искомой величины;
• проверить решение.

Основные формулы раздела «Термодинамика»