Математика
5 класс
Урок №32
Объём прямоугольного параллелепипеда. Единицы объёма
Перечень рассматриваемых вопросов:
– куб;
– параллелепипед;
– элементы параллелепипеда;
– объём прямоугольного параллелепипеда, куба.
Тезаурус
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками.
Высота, длина и ширина – это измерения прямоугольного параллелепипеда.
Единичный куб – куб, ребро которого равно линейной единице.
Обязательная литература
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Как вы думаете, что больше занимает места– 1 кг ваты или 1 кг гвоздей? Чтобы ответить на этот вопрос, нужно знать величину, которая называется объём. В данной задаче ответ очевиден, так как мы можем представить предметы визуально. Но не всегда ответ может быть таким простым. Чаще всего нужно произвести определённые вычисления.
Сегодня мы рассмотрим объём прямоугольного параллелепипеда и научимся его находить.
Объём можно измерить. Его измеряют в кубических миллиметрах, кубических сантиметрах, кубических метрах, литрах и т. д.
Найдём соотношение между единицами измерения объёма.
Так как 1 см = 10 дм, то 1 см3 = 1 000 мм3.
1 дм3 = 1000 см3 = 1 л
1 м3 = 1000 дм3
1 км3 = 1000000000 м3
В древности в разных частях планеты люди по-разному измеряли объём. Например, в Древней Греции использовали глиняные мерные сосуды для зерна или жидкостей. Причём это были амфоры разного размера. Поэтому значение единицы объёма менялось от 2 до 26 литров.
На Руси основной мерой жидкостей считалось ведро, в котором 10 кружек или 12 литров. Также для подсчётов объём ведра делили пополам, то есть на два полуведра, которые, в свою очередь, тоже можно было поделить пополам. Для торговли с иностранцами использовали меру объёма, называемую бочка, которая равнялась 40 вёдрам.
Дадим определение единичного куба – это куб, ребро которого равно линейной единице. Его тоже принимают за единицу объёма.
Если прямоугольный параллелепипед можно разрезать на К единичных кубов, то говорят, что его объём V равен К кубическим единицам.
Например, на рисунке объём параллелепипеда равен 24 кубическим единицам.

V = 24 куб. единиц
Введём формулу объёма прямоугольного параллелепипеда.
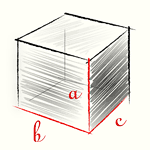
Объём прямоугольного параллелепипеда равен произведению трёх его измерений, то есть произведению длины а, ширины bи высоты c, или произведению площади основания S на высоту c.
V = а · b · c = S · с
Так как куб является прямоугольным параллелепипедом, у которого все измерения равны, то его объём равен третьей степени длины его ребра а.
V = а3
Решим задачу.
Мальчик купил аквариум в форме прямоугольного параллелепипеда, который имеет площадь дна, равную 1400 см3, и высоту 6 дм. Какой объём воды он налил в аквариум, если уровень жидкости не доходил до края 5 см? Выразите ответ в кубических сантиметрах.
Чтобы решить эту задачу переведём единицы измерения длины в сантиметры.
6 дм = 60 см
Получается, что высота аквариума равна 60 см. Но по условию задачи требуется определить объём налитой жидкости, а её высота соответствует разности между высотой аквариума и уровнем жидкости, не доходящей до края:
с = 60 см – 5 см = 55 см
Получается, что высота жидкости в сосуде соответствует 55 см.
Теперь можно определить объём воды, которая налита в аквариум.
Для этого используем следующую формулу:
V = S · с = 1400 см2 · 55 см = 77000 см3
Ответ: мальчик налил в аквариум 77000 см3 воды.
Разбор решения заданий тренировочного модуля
№ 1. Чему равен объём куба, если длина его ребра равна 3 см?
Решение: для нахождения объёма куба нужно воспользоваться формулой.
V = а3 = (3 см)3 = 27 см3
Ответ: 27 см3.
№2. Как изменится объём прямоугольного параллелепипеда, если его длину увеличить в три раза. Подчеркните правильный ответ.
Решение: чтобы ответить на вопрос, нужно воспользоваться формулой для вычисления объёма прямоугольного параллелепипеда.
V = а · b · c, где а – длина прямоугольного параллелепипеда.
Если длина возрастет в три раза, то объём, соответственно, увеличится в три раза, так как, длина – это один из трёх множителей, входящих в формулу объёма прямоугольного параллелепипеда:
V = 3 · а · b · c
Ответ: объём увеличится в три раза.
Уже известны единицы измерения длины, например:
— и другие.
Для фигур на плоскости измеряют площадь в соответствующих квадратных единицах измерения:
мм2,см2,дм2,м2,км2…
Для геометрических тел измеряют объём, и для этого необходимы единицы измерения.
Единицей измерения объёма служит объём куба, у которого все грани равны (1) единице измерения длины:

мм3,см3,дм3,м3,км3…
Это кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр или даже кубический километр:
1км3=1000000000м3;1м3=1000дм3=1000000см3;1дм3=1000см3;1см3=1000мм3.
Часто для измерения объёма жидкости используют единицу измерения (1) литр:
1 л =1000см3=1дм3
.
Если измерять объём прямоугольного параллелепипеда, то можно представить, как маленькие кубики перекрывают прямоугольник в основании прямоугольного параллелепипеда.
Длины сторон прямоугольника определяют, сколько кубиков в ряду и сколько рядов с кубиками будет.
|
|
|
Если стороны равны, например, (3) см и (4) см, то прямоугольник перекрывается (3·4 = 12) кубиками.
Высота параллелепипеда определяет, сколько таких слоёв с кубиками можно поставить.
 |
|
Если высота прямоугольного параллелепипеда равна (3) см, то всего получится (3) слоя с кубиками. Итак, всего (3·3·4 = 36) кубиков, или объём равен (36) см³.
Значит, три измерения прямоугольного параллелепипеда позволяют посчитать, сколько всего кубиков поместилось в геометрическом теле, то есть вычислить объём прямоугольного параллелепипеда.
Пусть измерения прямоугольного параллелепипеда будут a, b и c единиц измерения.
Тогда объём (V = a·b·c) кубических единиц измерения.
Объем прямоугольного параллелепипеда


4.7
Средняя оценка: 4.7
Всего получено оценок: 510.
4.7
Средняя оценка: 4.7
Всего получено оценок: 510.
В школьном курсе математики за 5 класс, ученики знакомятся с темой прямоугольного параллелепипеда. Это одна из первых фигур курса, имеющих объем. Именно об объеме и формуле его нахождения пойдет речь сегодня.

Опыт работы учителем математики – более 33 лет.
Определения
Прямоугольным параллелепипедом называется фигура, все грани которого – прямоугольники. Фигура имеет шесть граней. Грани, пресекаясь, образовывают ребра, их 12.
Прямоугольный параллелепипед имеет четыре боковые грани и две грани оснований. В жизни мы часто сталкиваемся с данной фигурой: шкаф, холодильник, коробка – все они имеют форму прямоугольного параллелепипеда.
Формула объема данной фигуры
Объем куба (фигуры, все грани которого квадраты) со стороной 1 единица называется 1 кубическая единица.

Если заложить такими кубиками дно фигуры (рис. 3), то в длину понадобится 4 куба, а в ширину 3.
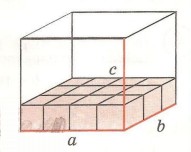
Таким образом, для заполнения основания необходимо:
3 х 4 =12 – так мы вычисляли площадь.
Чтобы заполнить всю фигуру и узнать объем, необходимо посчитать, сколько поместится в высоту таких слоев кубов, к примеру, если это будет 2, то объем составит:
3 х 4 х 2 = 24 кубов
Так, если учесть что длина основания фигуры 4 единицы, ширина – 3, высота – 2, то для того чтобы вычесть объем прямоугольного параллелепипеда необходимо найти произведение этих величин или измерений. Фигура, которая имеет три измерения, называется трехмерной либо объемной.
Для обозначения объема используют букву V.
Формула объема прямоугольного параллелепипеда имеет вид:
$$V = a · b · c$$
При необходимости все данные в задании необходимо перевести в одни единицы измерения.
Единицами измерения являются $мм^3, см^3, дм^3$ и так далее. Важно правильно читать: $1 м^3$ или кубический метр и так далее.
Английский иллюзионист провел 44 дня в стеклянном прямоугольном параллелепипеде, который был подвешен над рекой Темза. В его распоряжении была только вода, подушка, матрас и письменные принадлежности.
Задание: Вычислить объем фигуры, ширина которой 4 дм, длина 50 мм, а высота 10 см.
Решение: Для начала необходимо перевести все данные в одни единицы измерения.
$4 дм. = 40 см$;
$50 мм. = 5 см$.
$V = a • b • h$
$V = 40 • 5 • 10 = 200 см^3$
Таким образом, объем фигуры $V = 200 см^3$
Для измерения объема жидкости используют особую единицу измерения – литр (1 л).
Древние измерения жидкости, например кор = 220 л, бат = 22 л.
Измерения объема:
$$1 л = 1 000 см^3 = 1 дм^3$$
$$1 км^3 = 1000 000 000 м^3$$
$$1 м^3 = 1 000 дм^3 = 1 000 000 см^3$$
$$1 дм^3 = 1 000 см^3$$
$$1 см^3 = 1 000 мм^3$$

Что мы узнали?
Мы узнали, что для того, чтобы найти объем прямоугольного параллелепипеда необходимо умножить произведение длины и ширины основания на высоту фигуры. А также мы познакомились с единицами измерения объема.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Каролина Юсупова
5/5
-

Розочка Ангелиночка
5/5
-

Семён Сапьянов
4/5
-

Ярослава Ковалко
5/5
-

Армине Оганджанян
5/5
-

Егор Плисовский
4/5
-

Анастасия Прибыток
5/5
-

Lol Kek
5/5
-

Кирилл Лазарев
5/5
-

Илья Юрченко
5/5
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 510.
А какая ваша оценка?
На этом уроке мы познакомимся с понятием «объём», узнаем, как вычислить объём прямоугольного параллелепипеда и объём куба, а также поговорим о единицах измерения объёма.
Что такое объём?
На рисунке 1 вы видите стакан. Если использовать его как формочку для песка, получится цилиндрик. Таких цилиндров можно сделать много, и у всех их будет одинаковый объём. Если теперь налить в стакан воды, молока, сока, то объём жидкости будет равен объёму фигурки из песка.
Объём – это количественная характеристика пространства, которое занимает тело или вещество.
Другими словами, объём – это то, что куда-то вмещается. Объём можно измерить, объёмы можно сравнивать.
Сравним объём трёх чашек (рисунок 2). Объём синей чашки меньше всего, ведь она самая маленькая. А вот с зелёной и жёлтой чашкой не так всё просто. Зелёная – широкая, зато красная – высокая. Как бы вы узнали, объём какой чашки больше?
Показать решение
Скрыть
Простой способ — использовать воду или другую жидкость.
Нужно налить воду в одну из чашек, например, зелёную, и перелить её в красную. Если она будет полной, а зелёная чашка опустеет, значит, объём этих чашек равен. Если воды не хватит, чтобы заполнить вторую чашку, значит, объём первой чашки меньше, а если останется лишняя вода – значит, объём первой чашки больше.
Измерение объёма
В древности люди измеряли объём мерками, вёдрами, бочками… Даже сейчас в книгах рецептов часто можно встретить инструкции: «Возьмите стакан муки, чайную ложку соды и две столовые ложки сахара».
Обычно для измерения объёма, как и для измерения длины и площадей, используется метрическая система.
На рисунке 3 – куб, каждая сторона которого равна $1$ см. Объём этого куба будет $1$ см3, или один кубический сантиметр.
Для измерения объёмов используют следующие единицы: кубический миллиметр (мм3), кубический сантиметр (см3), кубический дециметр (дм3), кубический метр (м3), кубический километр (км3).
Кубический дециметр также называют литром.
Вычисление объёма
Предположим, у нас есть вот такая прозрачная коробка и маленькие кубики с ребром $1$ см.
Как найти объём коробки?
Показать решение
Скрыть
Положить в неё кубики и посчитать, сколько кубиков поместится.
У нас получился вот такой прямоугольный параллелепипед. Его длина $4$ кубика, ширина $3$ кубика, высота $2$ кубика.
Для удобства можно разбить этот прямоугольный параллелепипед на два слоя. Слои состоят из трёх рядов, а каждый ряд – из четырёх кубиков.
Объём каждого ряда будет $4$ см3, каждого слоя из трёх рядов – $4 cdot 3$ (см3), а всей фигуры — $(4 cdot 3) cdot 2$, то есть $24$ см3.
Для того чтобы вычислить объём прямоугольного параллелепипеда, нужно его длину умножить на ширину и на высоту.
$$V=abc$$
А как найти объём куба?
Показать решение
Скрыть
Все его измерения одинаковы. Значит, формула объёма куба будет выглядеть так:
$$V=a^3$$
Именно поэтому третью степень числа (n3) называют кубом числа n.
Нахождение объема куба: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a 3

2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√ 2 .

Следовательно, вычислить объем куба можно так:
![]()
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .
Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:![]()
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
Как вычислить объем куба
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 82 человек(а).
Количество просмотров этой статьи: 562 175.
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте). У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 , где s — длина одного (любого) ребра куба.
Объемы фигур. Объем куба.
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте).
У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны.
Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна
ширине и равна высоте, то объем куба равен s 3 ,

где s – длина одного (любого) ребра куба.
Воспользуйтесь онлайн калькулятором для расчета объема куба: объем куба, онлайн расчет.
Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.
Метод 1 из 3: Возведение в куб ребра куба
- Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы
вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.
Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.
Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза.
Если s — длина ребра куба, то

и, таким образом, вы вычислите объем куба.
Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на
ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть,
другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и
равна высоте, то это процесс можно заменить возведением ребра куба в третью степень.
В нашем примере объем куба равен:

- К ответу припишите единицы измерения объема. Так как объем – это количественная
характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические
В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических
сантиметрах (или в см 3 ). Итак, объем куба равен 125 см 3 .
Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих
Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м 3 .
Метод 2 из 3: Вычисление объема по площади поверхности
- В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых вы
можете найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите
ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем
возведите длину ребра куба в третью степень и вычислите объем куба.
Площадь поверхности куба равна 6s 2 ,
где s – длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так
как у куба 6 равных граней).
Рассмотрим пример. Площадь поверхности куба равна 50 см 2 . Найдите объем куба.
- Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь
одной грани куба). В свою очередь площадь одной грани куба равна s 2 , где s – длина ребра куба.
В нашем примере: 50/6 = 8,33 см 2 (не забывайте, что площадь измеряется в квадратных единицах — см 2 ,
- Так как площадь одной грани куба равна s 2 , то извлеките квадратный корень из значения площади
одной грани и получите длину ребра куба.
В нашем примере, √8,33 = 2,89 см.
- Возведите в куб полученное значение, чтобы найти объем куба.
В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см 3 . К ответу не забудьте приписать кубические
Метод 3 из 3: Вычисление объема по диагонали
- Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом,
если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив
Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба
равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см 3 .
Запомните: d 2 = 2s 2 ,
где d — диагональ грани куба, s – ребро куба. Эта формула вытекает из теоремы Пифагора, согласно
которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен
сумме квадратов катетов (в нашем случае ребер), то есть:
d 2 = s 2 + s 2 = 2s 2 .
- Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче
дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3.
Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный
(где D — диагональ куба, s – ребро куба).
Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае
диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет –
это ребро, а второй катет – это диагональ грани куба, равная 2s 2 ), то есть
D 2 = s 2 + 2s 2 = 3s 2 .
Рассмотрим пример. Диагональ куба равна 10 м. Найдите объем куба.



