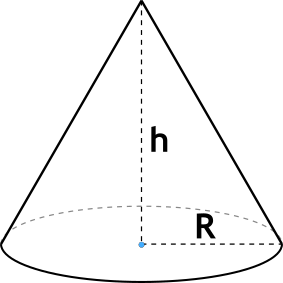
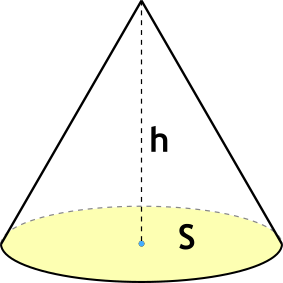
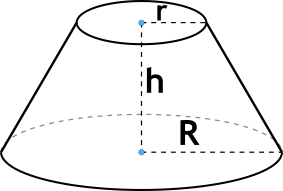
Конус – это тело в пространстве, образованное путем вращения прямоугольного треугольника вокруг одного из его катетов.
Онлайн-калькулятор объема конуса
Конус – это тело, образованное совокупностью всех лучей, исходящих из точки пространства и пересекающих плоскость.
Точка, из которой лучи исходят, получила название вершины конуса. В случае, когда основанием конуса является многоугольник, он превращается в пирамиду.
Рассмотрим некоторые важные понятия.
Образующей конуса называется отрезок, который соединяет любую точку границы основания конуса, с его вершиной.
Высотой конуса является перпендикуляр, который опущен из вершины к основанию тела.
Конус бывает нескольких типов:
Прямой, если его основание – одна из таких фигур, как эллипс или круг. Обязательным условием является проецирование вершины конуса в центр основания.
Косой – у него центр фигуры, которая находится в основании, не совпадает с проекцией вершины на это самое основание.
Круговой – отталкиваясь от названия, понятно, что в его основании лежит круг.
Усеченный – область конуса, лежащая между основанием и сечением плоскости, которая параллельна основанию и пересекает данный конус.
Формула объема прямого конуса
Объем прямого конуса можно рассчитать по следующей формуле:
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
где SоснS_{text{осн}} – площадь основания конуса;
hh – высота конуса.
Рассмотрим несколько примеров.
Найдите объем конуса, если его образующая ll равна 5см5text {см}, а радиус основания RR, которым является круг, равен 3 см3text{ см}.
Решение
l=5l=5
R=3R=3
Сперва найдем высоту конуса hh. Включим его в прямоугольный треугольник, гипотенузой которого является образующая. По теореме Пифагора:
l2=h2+R2l^2=h^2+R^2
Отсюда, hh:
h=l2−R2h=sqrt{l^2-R^2}
h=52−32h=sqrt{5^2-3^2}
h=25−9h=sqrt{25-9}
h=16h=sqrt{16}
h=4h=4
Затем находим площадь основания конуса. Это площадь круга радиуса RR:
Sосн=π⋅R2=π⋅32≈28.26S_{text{осн}}=picdot R^2=picdot3^2approx28.26
Последние вычисления — нахождение объема конуса по формуле:
V=13⋅Sосн⋅h≈13⋅28.26⋅4≈37.68 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 28.26cdot 4approx37.68text{ см}^3
Ответ: 37.68 см3.37.68text{ см}^3.
Известен диаметр круга DD лежащего в основании конуса, равен он 8 см8text{ см}. Высота конуса равна 9 см9text{ см}. Найдите его объем.
Решение
D=8D=8
h=9h=9
Найдем радиус RR круга через его диаметр:
R=12⋅D=82=4R=frac{1}{2}cdot D=frac{8}{2}=4
Площадь этого круга и есть основание нашего конуса:
Sосн=π⋅R2=π⋅42≈50.24S_{text{осн}}=picdot R^2=picdot4^2approx50.24
Сам объем равен:
V=13⋅Sосн⋅h≈13⋅50.24⋅9≈150.72 см3V=frac{1}{3}cdot S_{text{осн}}cdot happroxfrac{1}{3}cdot 50.24cdot 9approx150.72text{ см}^3
Ответ: 150.72 см3.150.72text{ см}^3.
Вам нужно решить задачу по алгебре? Наши эксперты помогут вам!
Тест на тему “Объем конуса”
В данной публикации мы рассмотрим, каким образом можно посчитать объем прямого кругового конуса и разберем примеры решения задач.
-
Формула вычисления объема
- 1. Через площадь основания и высоту
- 2. Через радиус основания и высоту
-
Примеры задач
Формула вычисления объема
1. Через площадь основания и высоту
Объем (V) конуса равняется одной третьей произведения его высоты на площадь основания:
2. Через радиус основания и высоту
Как мы знаем, основанием конуса является круг, площадь которого вычисляется по формуле: S = πR2.
Следовательно, формулу для вычисления объема конуса можно представить в виде:
Т.е. объем конуса равняется одной третьей произведения его высоты на число π и на радиус основания в квадрате.
Примечание: в расчетах значение числа π округляется до 3,14.
Формула для нахождения объема усеченного конуса представлена в отдельной публикации.
Примеры задач
Задание 1
Найдите объем конуса, если известна площадь его основания – 50,24 см2, а также, высота – 9 см.
Решение:
Применим первую формулу, подставив в нее заданные значения:
Задание 2
Высота конуса равна 7 см, а его радиус – 3 см. Найдите объем фигуры.
Решение:
Воспользовавшись второй, более расширенной, формулой получаем:

{V=dfrac {1}{3} pi r^2 h}
Конус – это трехмерная фигура, в основании которой лежит круг. Чтобы найти объем конуса достаточно знать два параметра – высоту (h) и радиус основания (r).
Содержание:
- калькулятор объема конуса
- формула объема конуса через высоту и радиус
- формула объема конуса через площадь основания и высоту
- формула объёма усеченного конуса
- примеры задач
Если мы сравним формулу объема конуса с формулой объема цилиндра, то мы увидим, что объем конуса в 3 раза меньше объема цилиндра с той же высотой и радиусом основания.
Наш калькулятор может рассчитать объем конуса через радиус основания и высоту, площадь основания и высоту, а также объем усеченного конуса через его высоту и радиусы нижнего и верхнего оснований.
Кроме того объем конуса можено найти, подставив значения в формулы, приведенные ниже.
Формула объёма конуса через радиус и высоту
{V=frac {1}{3} pi r^2 h}
r – радиус основания конуса,
h – высота конуса
Формула объёма конуса через площадь основания и высоту
{V=frac {1}{3} S h}
S – площадь основания конуса,
h – высота конуса
Формула объёма усеченного конуса
{V=frac {1}{3} pi h(r^2 + r R + R^2)}
h – высота усеченного конуса,
r – радиус меньшего основания усеченного конуса,
R – радиус большего основания усеченного конуса.
Примеры задач на нахождение объема конуса
Задача 1
Найдем объем конуса, высота которого 30см, а радиус основания 20см.
Решение
Подставим эти значения в формулу и произведем расчет:
V=dfrac {1}{3} pi r^2 h = dfrac {1}{3} cdot pi cdot 20^2 cdot 30 = dfrac {1}{3} cdot pi cdot 12000 = 400 pi : см^3 approx 12 566,37 : см^3
Ответ: {400 pi : см^3 approx 12 566,37 : см^3}
Проверить результат можно с помощью калькулятора .
Задача 2
Найдем объем конуса с высотой 3 см и диаметром основания 8 см².
Решение
Подставим эти значения в формулу и произведем расчет:
V=dfrac {1}{3} S h = dfrac {1}{3} cdot 8 cdot 3 = dfrac {1}{3} cdot 24 = 8 : см^3
Ответ: 8 см³
Воспользуемся калькулятором для проверки результата.
Задача 3
Найдите объем усеченного конуса радиусы оснований которого равны 1 см и 2 см, а высота равна 3 см.
Решение
Подставим высоту и радиусы оснований в формулу и произведем расчет:
V=dfrac {1}{3} pi h(r^2 + r R + R^2) = dfrac {1}{3} pi cdot 3 cdot (1^2 + 1 cdot 2 + 2^2) = dfrac {1}{3} pi cdot 3 cdot (1 + 2 + 4) = dfrac {1}{3} pi cdot 3 cdot 7 = dfrac {1}{3} pi cdot 21 = 7 pi : см^3 approx 21,99115 : см^3
Ответ: {7 pi : см^3 approx 21,99115 : см^3}
Проверим полученный ответ.
Формулы объема и площади поверхности. Цилиндр, конус и шар

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.
Например, такой важный факт:
Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем – в 8 раз.
(ведь ,
).
Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.
1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.
Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в
раза больше.
Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или
у вас в ответе в части В быть не должно. Подставлять приближенное значение числа
тоже не нужно! Оно обязательно должно сократиться! Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на
».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.
Мы тоже расскажем о ней.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Формулы объема и площади поверхности. Цилиндр, конус и шар» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Как рассчитать объем конуса
На данной странице калькулятор поможет рассчитать объем конуса онлайн. Для расчета задайте высоту, радиус или площадь. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Конус – геометрическое тело, образованное вращением прямоугольного треугольника около одного из его катетов.
Через высоту и радиус
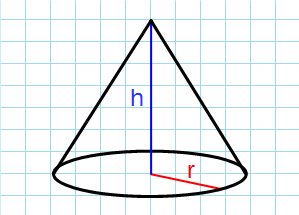
Формула объема конуса через радиус и высоту:
π – константа равная (3.14); h – высота конуса; r – радиус основания конуса.
Через высоту и площадь основания
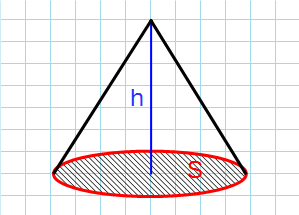
Формула объема конуса через высоту и площадь основания:
h – высота конуса; S – площадь основания.