Загрузить PDF
Загрузить PDF
Кубический сантиметр является единицей измерения объема, равной объему куба со стороной 1 см. Есть несколько способов вычислить объем предмета в кубических сантиметрах, но в простейшем случае — прямоугольного параллелепипеда — объем равен произведению длины на ширину на высоту.
-
1
Измерьте длину, ширину и высоту предмета (в сантиметрах). Для этого измерьте требуемые величины с помощью линейки или рулетки или конвертируйте известные вам значения в сантиметры.[1]
- Например, если вы хотите узнать объем холодильника, найдите его длину, ширину и высоту (в сантиметрах). Предположим, что ваш холодильник в высоту имеет 100 см, в ширину — 50 см, в длину — 40 см.
-
2
Запишите высоту предмета. Вы можете перемножать величины в любом порядке. Например, начните с высоты.
- В нашем примере запишите, что высота = 100 см.
-
3
Умножьте высоту на ширину. Затем умножьте первую величину на какую-нибудь из оставшихся (любую). Например, умножьте высоту на ширину.[2]
- В нашем примере, умножьте 100 на 50: 100 × 50 = 5000.
-
4
Умножьте полученный результат на длину предмета. Последний шаг — умножьте полученный результат на оставшуюся величину. Например, умножьте произведение высоты и ширины на длину.
- В нашем примере, умножьте 5000 на 40: 5000 × 40 =Н 200 000.
-
5
Запишите ответ в кубических сантиметрах, чтобы он был понятен любому человеку.
- Единицы измерения записываются так:
- кубические сантиметры
- сантиметров в кубе
- см^3
- см3
Реклама
- Единицы измерения записываются так:
-
1
Объем куба: V= L3, где V — объем, L — сторона. Куб – прямоугольный параллелепипед, у которого все стороны равны.[3]
Таким образом, формулу для вычисления объема куба можно записать в виде: длина × ширина × глубина = длина × длина × длина = длина3. Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах. -
2
Объем цилиндра: V = hπr2, где V — объем, h — высота, r — радиус цилиндра. Цилиндр — геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными круглыми плоскостями.[4]
Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах. -
3
Объем конуса: V = (1/3)hπr2, где V — объем, h — высота, r — радиус конуса. Конус — тело с круглым основанием и вершиной над ним. Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.[5]
-
4
Объем шара: V = 4/3πr3, где V — объем, r — радиус шара. Шар — абсолютно круглое тело.[6]
Чтобы получить объем в кубических сантиметрах, величины измеряйте в сантиметрах.Реклама
Советы
- Если вы не уверены в правильности ваших вычислений, проверьте ответ, воспользовавшись калькулятором или помощью другого человека, разбирающегося в математике.
- Кубические сантиметры — единица измерения объема, то есть количественной характеристики пространства, занимаемого телом.
- Для точного измерения величин используйте линейку или рулетку (особенно если вы делаете важные измерения).
Реклама
Об этой статье
Эту страницу просматривали 96 968 раз.
Была ли эта статья полезной?
Как найти объем через площадь
Объем – мера вместимости, выраженная для геометрических фигур в виде формулы V=l*b*h. Где l – длина, b – ширина, h – высота объекта. При наличии только одной или двух характеристик вычислить объем в большинстве случаев нельзя. Однако при некоторых условиях представляется возможным сделать это через площадь.

Инструкция
Задача первая: вычислить объем, зная высоту и площадь. Это самая простая задача, т.к. площадь (S) – это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.Пример: Площадь одной из сторон параллелепипеда – 36 см², высота – 10 см. Найдите объем параллелепипеда.V = 36 см² * 10 см = 360 см³.Ответ: Объем параллелепипеда равен 360 см³.
Задача вторая: вычислить объем, зная только площадь. Это возможно, если вы вычисляете объем куба, зная площадь одной из его граней. Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.Пример: площадь одной грани куба – 36 см². Вычислите объем.Извлеките квадратный корень из 36 см². Вы получили длину – 6 см. Для куба формула будет иметь вид: V = a³, где а – ребро куба. Или V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.V = 36 см² * 6 см = 216 см³. Или V = 6³см = 216 см³.Ответ: Объем куба равен 216 см³.
Задача третья: вычислить объем, если известна площадь и некоторые другие условия. Условия могут быть разные, помимо площади могут быть известны другие параметры. Длина или ширина могут быть равны высоте, больше или меньше высоты в несколько раз. Также могут даваться дополнительные сведения о фигурах, которые помогут в вычислениях объема.Пример 1: найдите объем призмы, если известно, что площадь одной стороны 60 см², длина 10 см, а высота равна ширине.S = l * b; l = S : b
l = 60 см² : 10 см = 6 см – ширина призмы. Т.к. ширина равна высоте, вычислите объем:
V=l*b*h
V = 10 см * 6 см *6 см = 360 см³Ответ:объем призмы 360 см³
Пример 2: найдите объем фигуры, если площадь 28 см², длина фигуры 7 см. Дополнительное условие: четыре стороны равны между собой, и соединены друг с другом по ширине.Для решения следует построить параллелепипед. l = S : b
l = 28 см² : 7 см = 4 см – ширинаКаждая сторона представляет собой прямоугольник, длина которого 7 см, а ширина 4 см. Если четыре таких прямоугольника соединить между собой по ширине, то получится параллелепипед. Длина и ширина в нем по 7 см, а высота 4 см. V = 7 см * 7 см * 4 см = 196 см³Ответ: Объем параллелепипеда = 196 см³.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Посчитать объём коробки
- Главная
- /
- Логистика
- /
- Посчитать объём коробки
Чтобы посчитать объем коробки или нескольких коробок воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
Расчет объема коробки
Длина коробки
Ширина коробки
Высота коробки
Объем коробки:
0
Просто введите длину, ширину и высоту коробки и узнаете её объём.
Расчет объема нескольких коробок
Количество коробок
шт
Длина коробки
Ширина коробки
Высота коробки
Объем одной коробки:
0
Общий объем всех коробок:
0
Теория
Коробка это прямоугольный параллелепипед, который имеет длину A, ширину B и высоту (глубину) C. Её объём считается по следующей формуле:
Формула
V = A⋅B⋅C
Пример
К примеру, возьмём коробку, у которой ширина равна 56 см, высота – 40 см, глубина – 32 см и посчитаем её объём:
V = 56⋅40⋅32 = 71680 см³
Если нам необходимо знать объём в кубометрах, нужно полученную цифру разделить на 1 000 000:
V = 71680/1000000 = 0.07168 ≈ 0.07 м³
См. также
Калькулятор для расчета объема параллелепипеда
C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер “a”, “b”, “c” и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
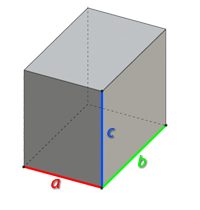
Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку “Рассчитать”
Округлить результат до
знаков после запятой
Рассчитать
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
где a, b, c – ребра параллелепипеда.
- Какой котлован нужно вырыть для погреба или фундамента?
- Как узнать вместимость комнаты?
В расчетах поможет калькулятор объема в м3. Он пригодится в расчете объема прямоугольного параллелепипеда или куба, достаточно ввести данные в поля и узнать результат.
Справка. У прямоугольного параллелепипеда все грани являются прямоугольниками.
Формула объема, по которой ведется расчет:
V=a*b*c
Где:
- а – длина;
- b – ширина;
- c – высота.
Указано, что нужно вводить данные в метрах и результат получается в кубометрах (м3), но использовать можно любые системные единицы: мм, см или дм. Для конвертации используйте подсказки:
- 1 мм3 = 0,000000001 м3;
- 1 см3 = 0,000001 м3;
- 1 дм3 = 0,001 м3.
Калькулятор кубических метров — это простой и эффективный инструмент для расчета вместимости любой прямоугольной формы. Этот инструмент поможет вам быстро получить ответ и будет полезен как для практических работ, так и в учебе. Используйте онлайн-калькулятор объема и получайте точные данные.






