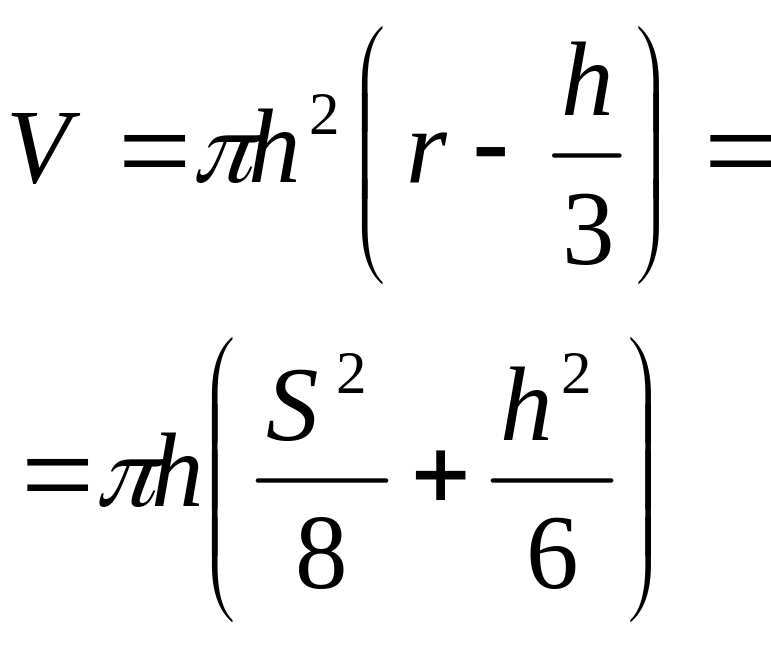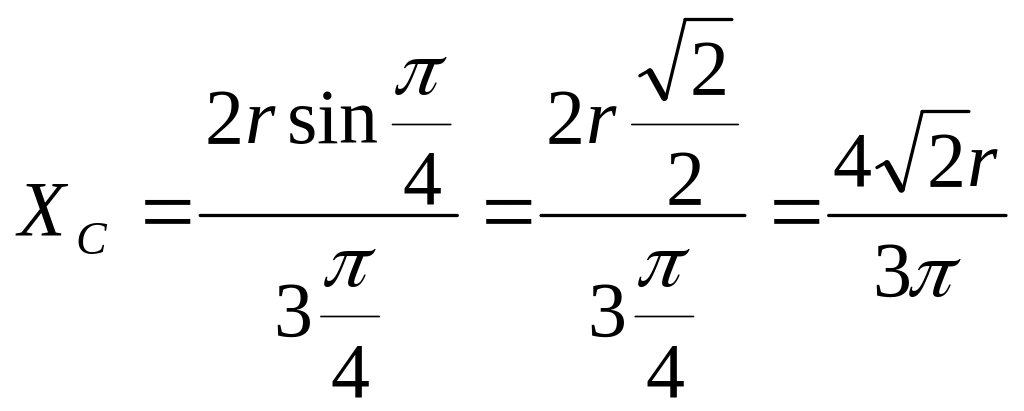Как найти объем вала

1. Определение массы детали по ее чертежу

Масса детали
определяется

G
= V,

где V
– объем детали, 
‑ плотность материала из которого
изготовлена данная деталь.

Таким образом,
для определения массы детали необходимо
определить объем детали. Для этого
разбиваем деталь на фигуры, для которых
можно определить объем детали по
известным формулам (табл. 2.1)

Таблица 2.1

Наим.	Наглядное изображение	Эскиз	Объем
1	2	3	4
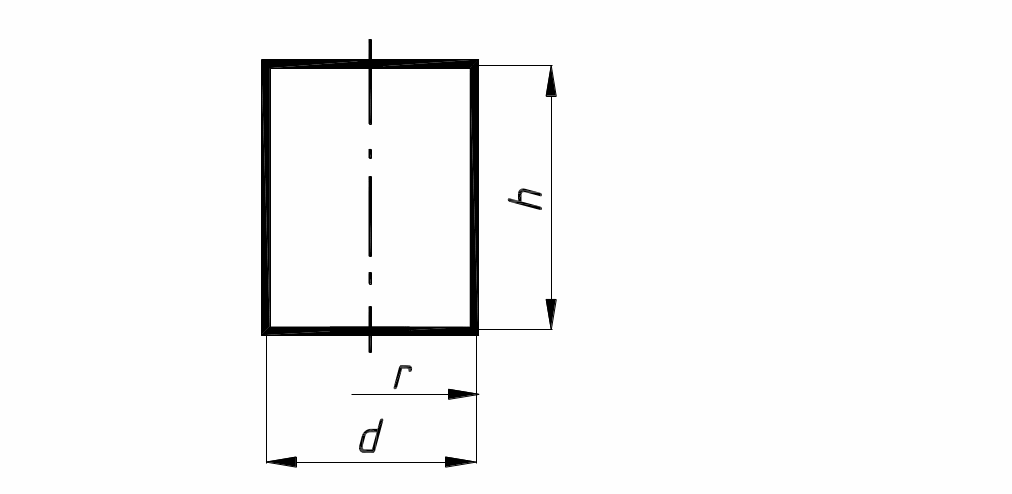
Цилиндр
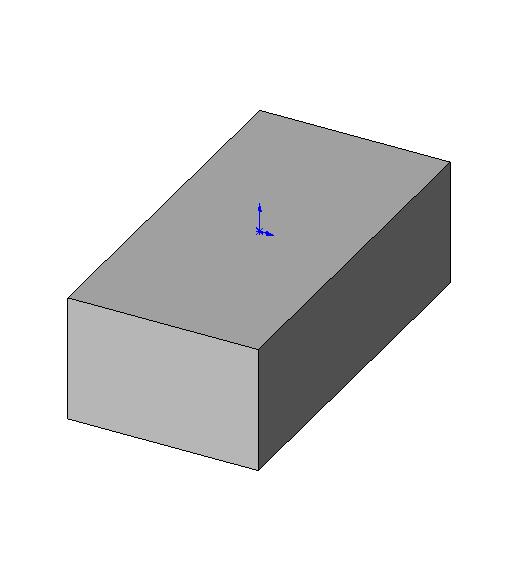
Призма			V = аbc
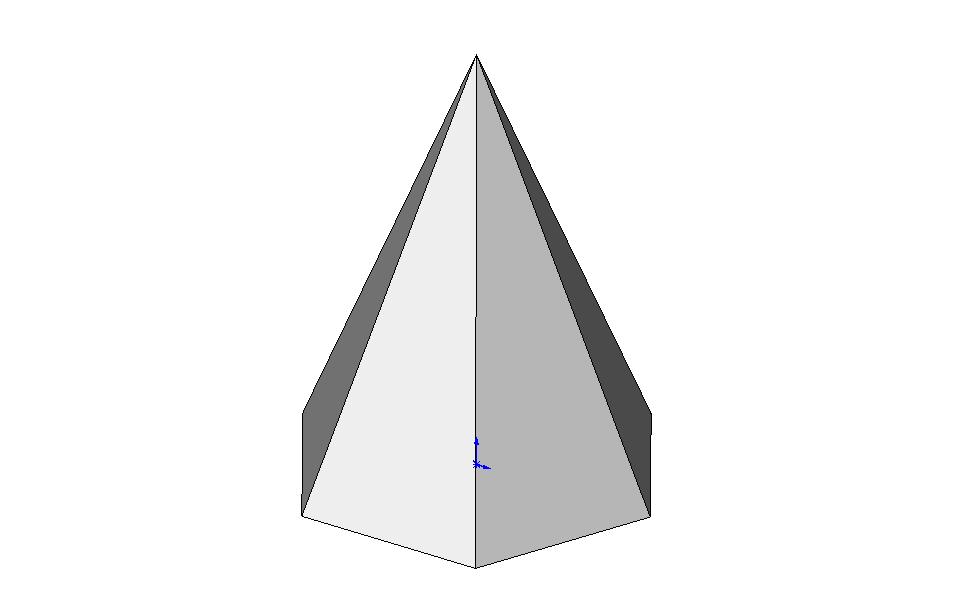
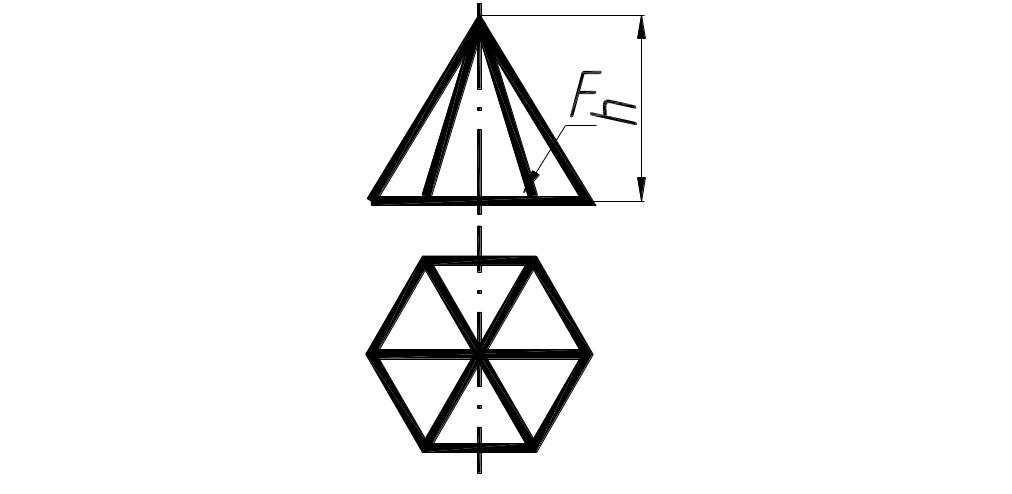
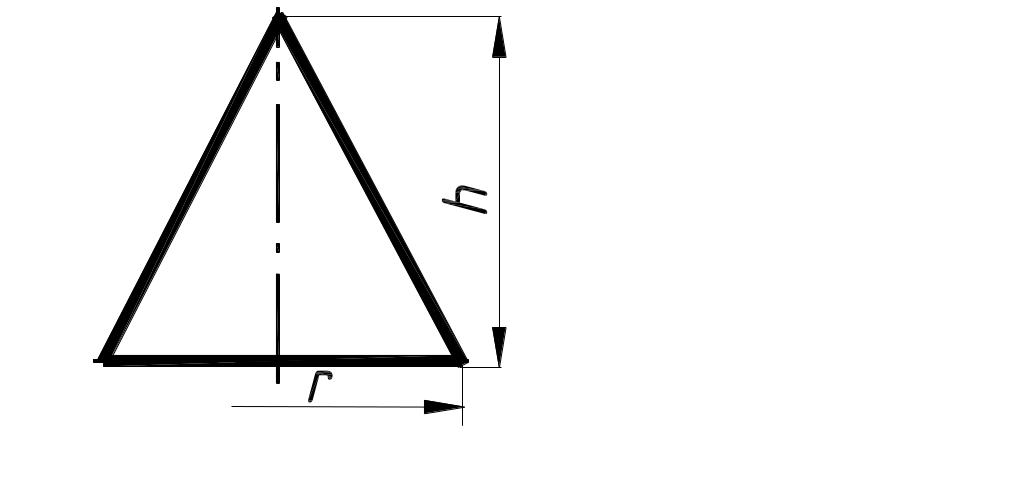
Пирамида			площадь основания

Продолжение табл.
2.1

1	2	3	4
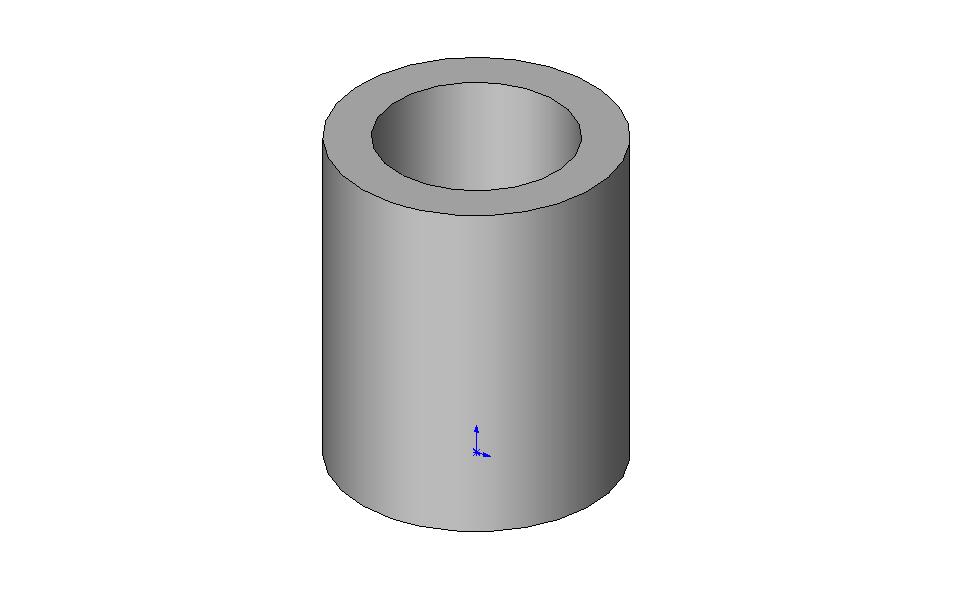
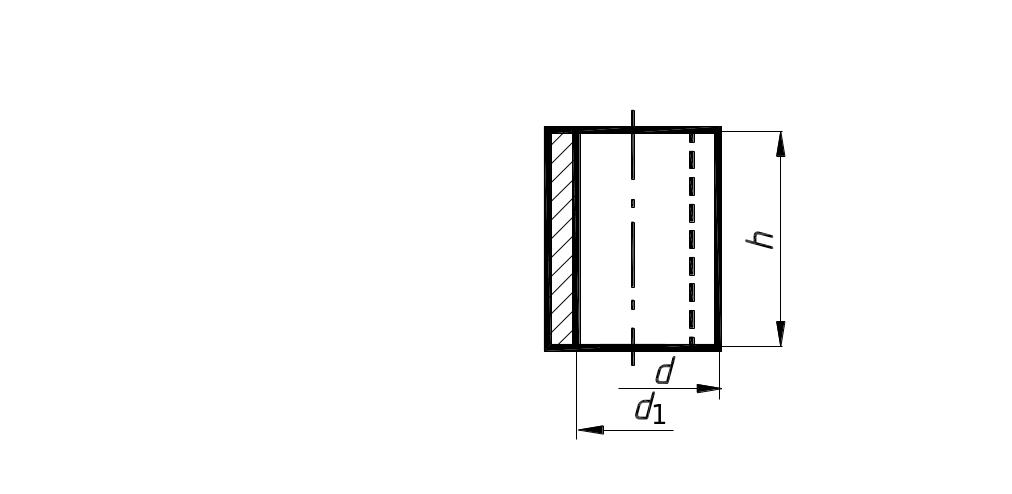
Полый цилиндр
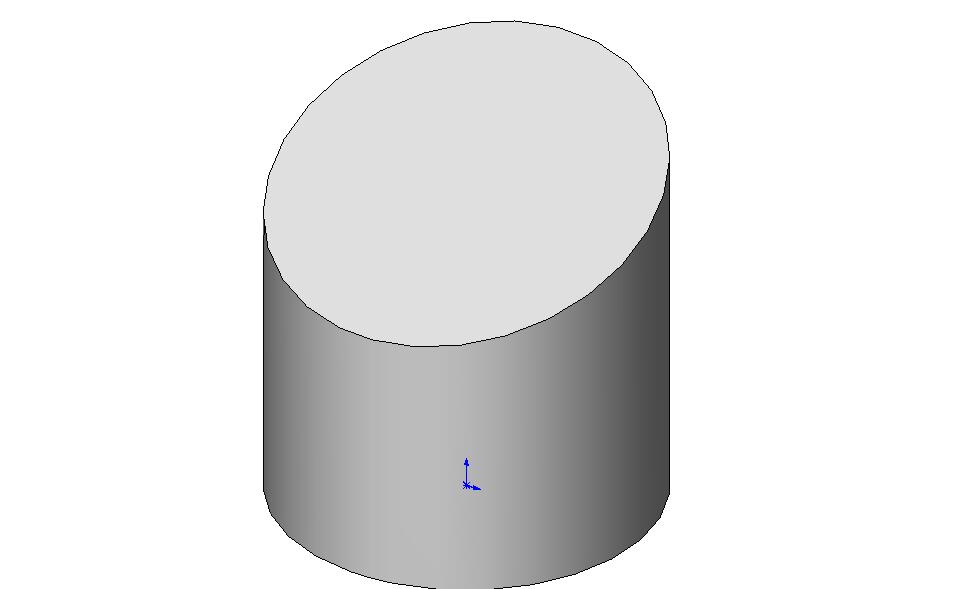
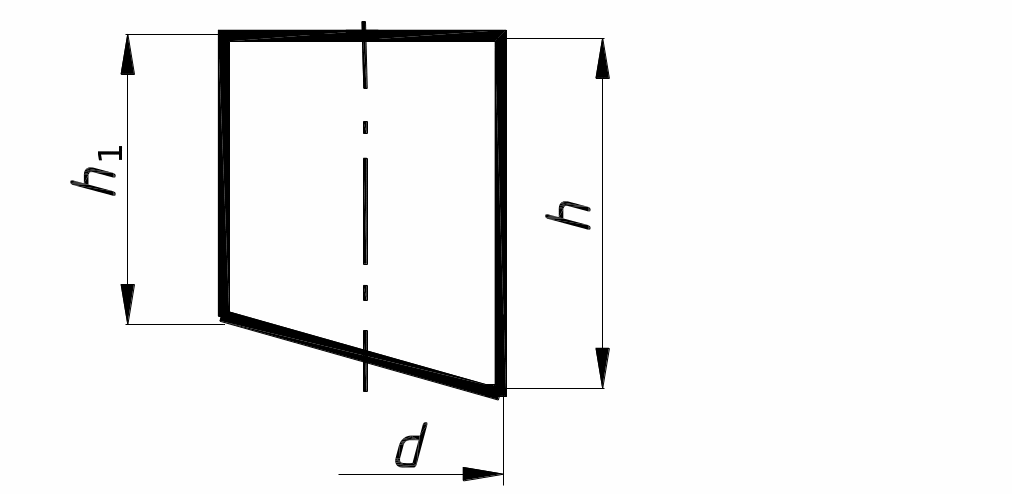
Косо срезанный цилиндр
Шар
Шаровой сектор
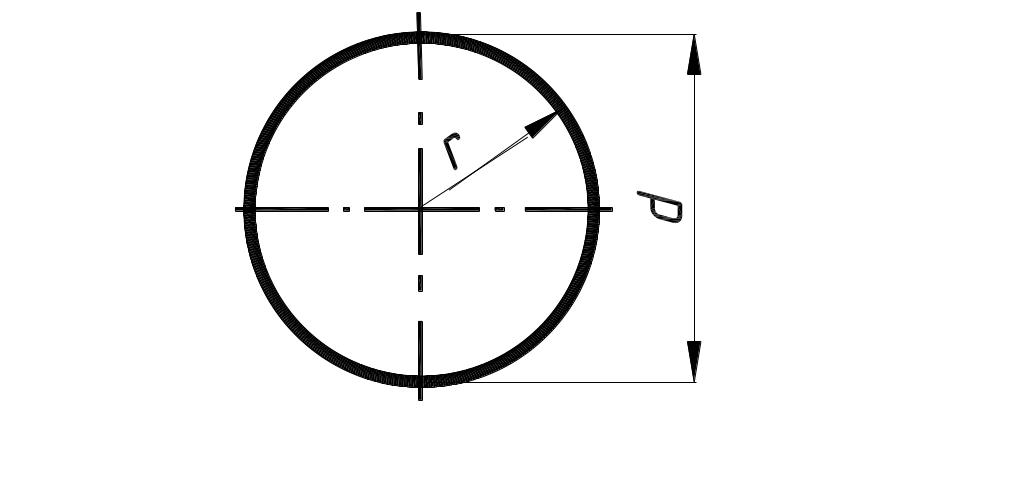
Шаровой сегмент

Продолжение табл.
2.1

1	2	3	4
Конус
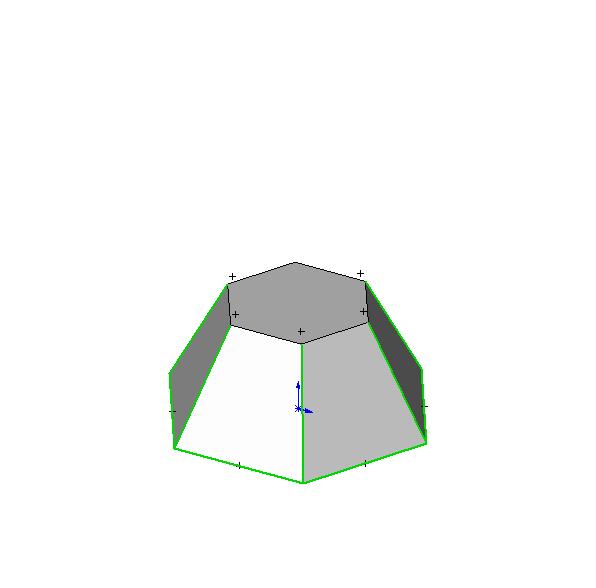
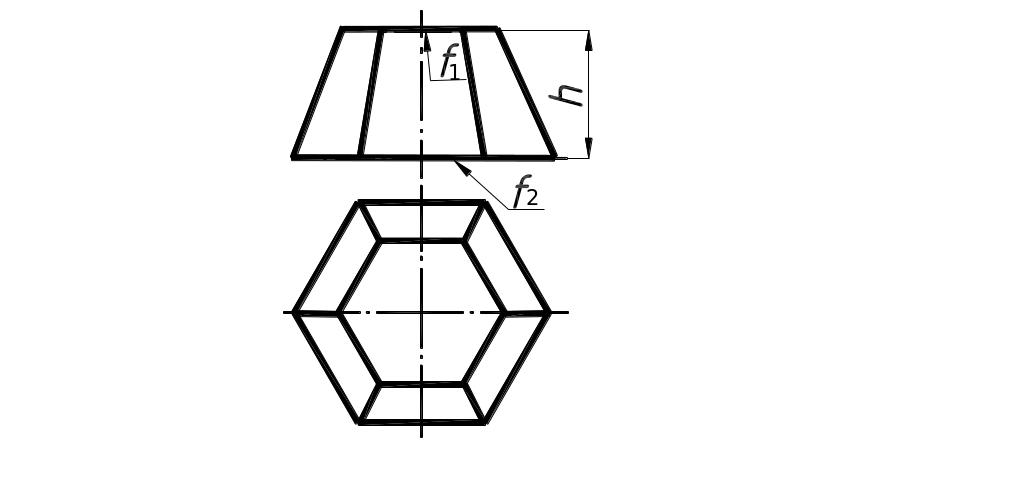
Усеченная пирамида			, где f1 и f2 – площади оснований пирамиды
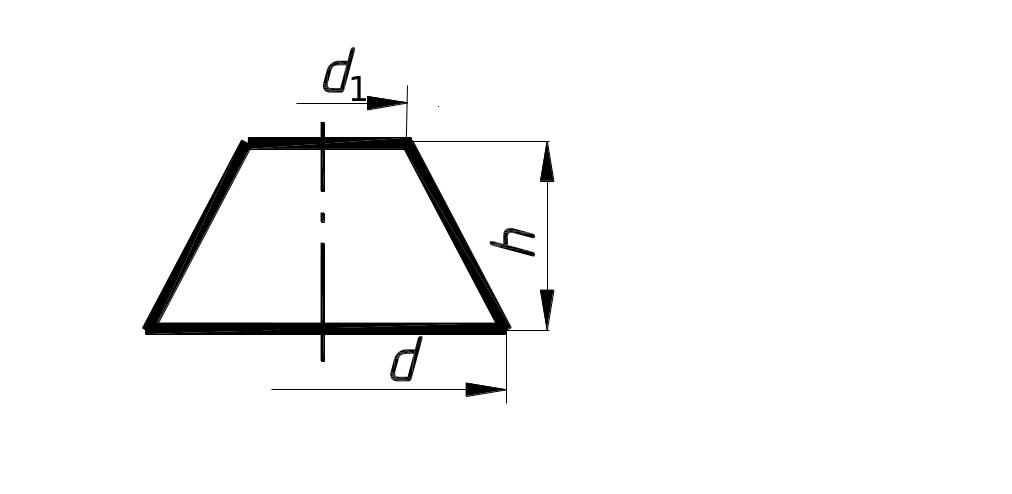
Усеченный конус
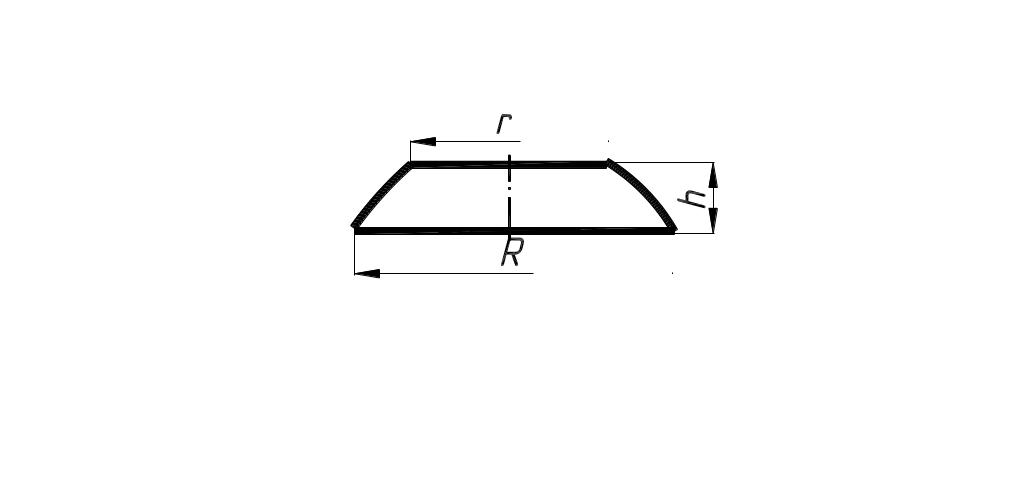
Бочка
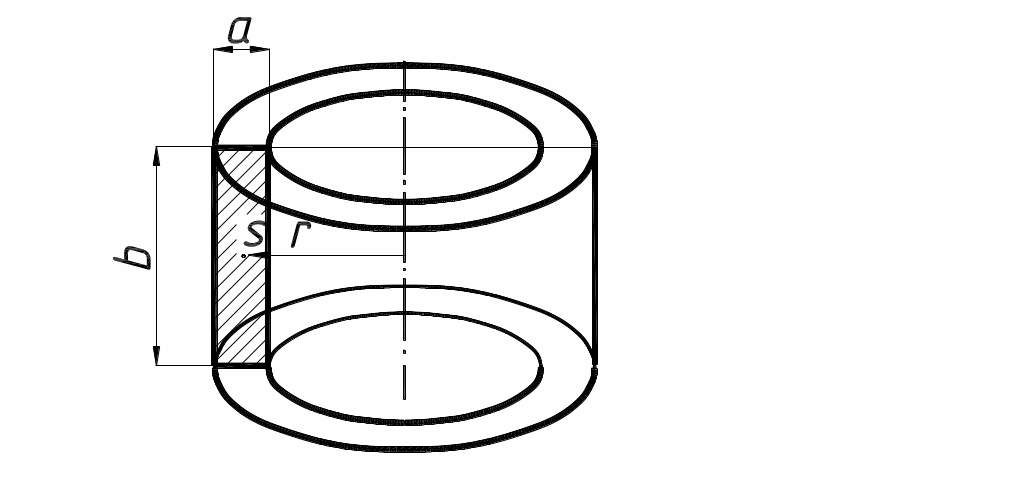
Тело вращения		Объем V тела вращения, образованного вращением площади F, умноженной на путь, описанный ее центром тяжести S вокруг оси радиусом r V=2rF=2rab

В качестве примера
рассмотрим определение объема вала,
изображенного на рис. 2.1. Разобьем вал
на простые (с точки зрения вычисления
объема) тела (рис. 2.2) и вычислим их объем.

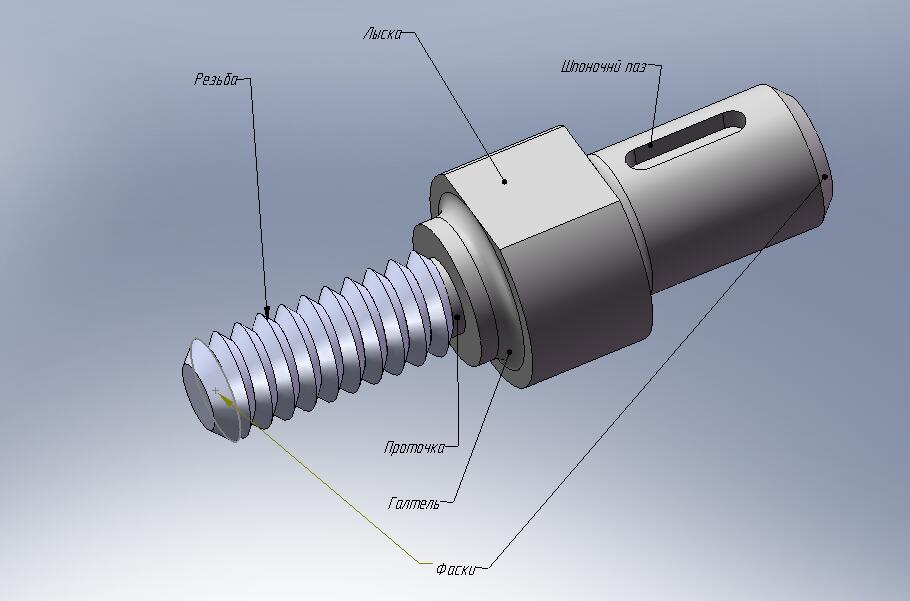
Рис.2.1

1. Объем фаски (1) –
усеченный конус (рис. 2.2)

,

где h
= 2 мм; r
= d/2=6
мм; r₁
= r
– 2 = 4 мм.

Тогда

.

1. Объем цилиндра
   (2)

.

Рис. 2.2

3. Объем паза (3) с
поперечным сечением S
(рис. 2.3, а)
и длиной 10 мм для призматической части
паза

а б

Рис. 2.3

,

где S
= S_сег.
+
S_пр,
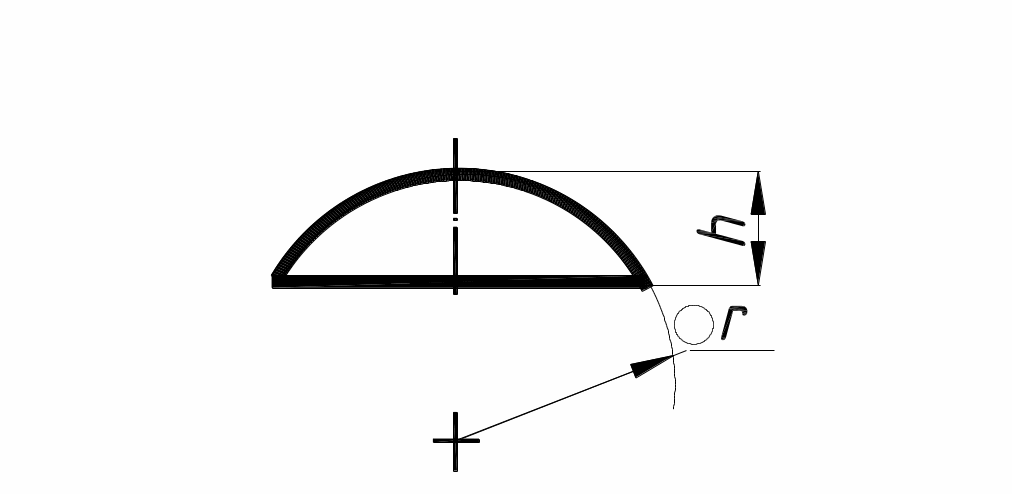
S_сег.
– площадь сегмента с радиусом R,
S_пр
– площадь прямоугольника b
ĥ
h,
б.
S_сег.
=
S_сек.
– S_тр.
S_сек.
– площадь
сектора круга, S_тр
– площадь треугольника – рис. 2.3

S_сег.
=
S_сек.
– S_тр=

здесь

S_пр
= b
ĥ
h
= 5∙10 = 50 мм²,

S
= S_сег.
+
S_пр
= 16,16 + 50 =66,16 мм²

.

Учтем объем цилиндра
от боковых полуцилиндров паза. Примем

r
=b/2
= 2,5 мм
– радиус цилиндра,

h^/
= h
+ 0,5(R
–

)
= 3 + 0,5(6 –


‑ высота

цилиндра равная
глубине паза и верхнюю часть цилиндра
паза.

Тогда объем
цилиндрической части шпоночного паза,
получим:

V_ц
≈
πr²h^/=π6,25∙3,27
= 64,2 мм³

Окончательно объем
шпоночного паза будет

V₃
= V_пр
+ V_ц
= 661,6+64,2 = 725,8 мм³

4. Объем галтели 4
с радиусом r
= 1 мм
(рис. 2.4).

Площадь галтели
определится как разность площадей
квадрата S_к
= r²
и четверти
круга (сектора) S_c
= r²/4
(рис. 2.4)

S_г
= r²
– r²/4
= r²(4-
)/4=
1²(4-π)/4
= 0,22 мм²

Р

ис.
2.4

Центр тяжести
вдоль оси Х
квадрата x_К
=

,
а четверти круга – сектора круга с углом
90º

,

Центр тяжести
галтели вдоль оси X:

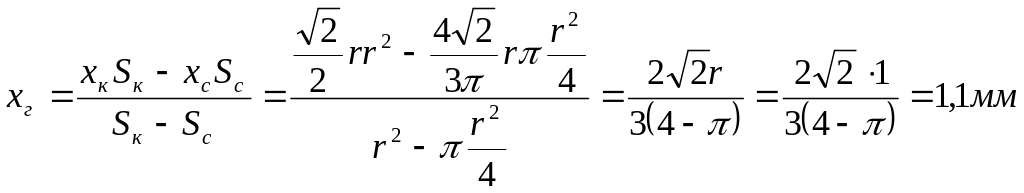
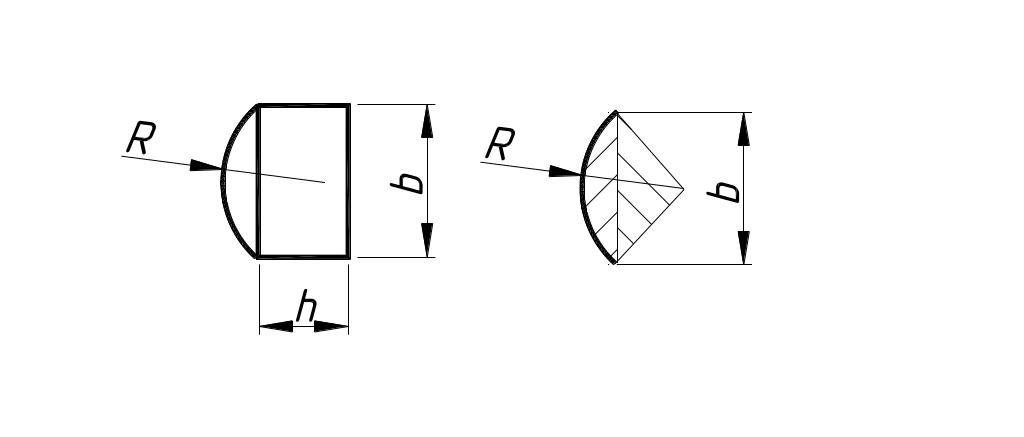
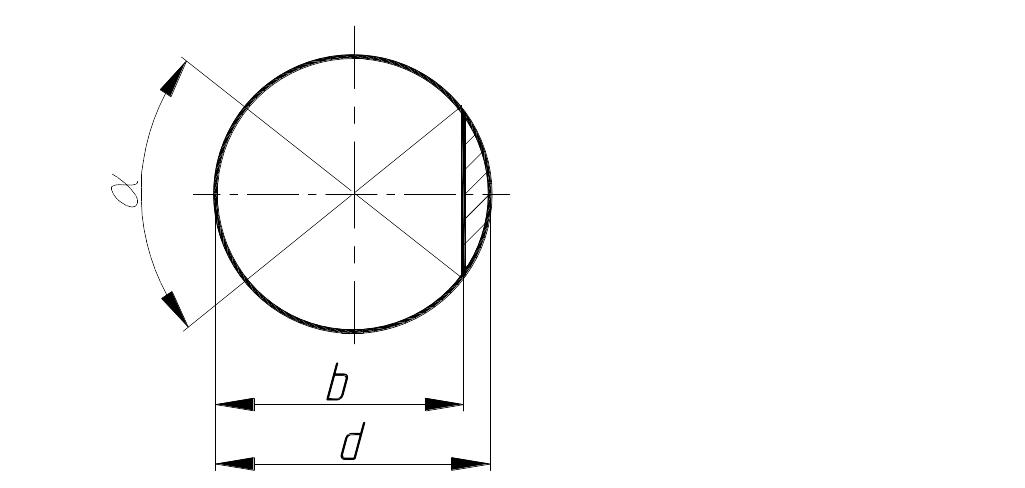
5. Объем лыски (рис.
2.5) 5:

V₅
= S_сег.h

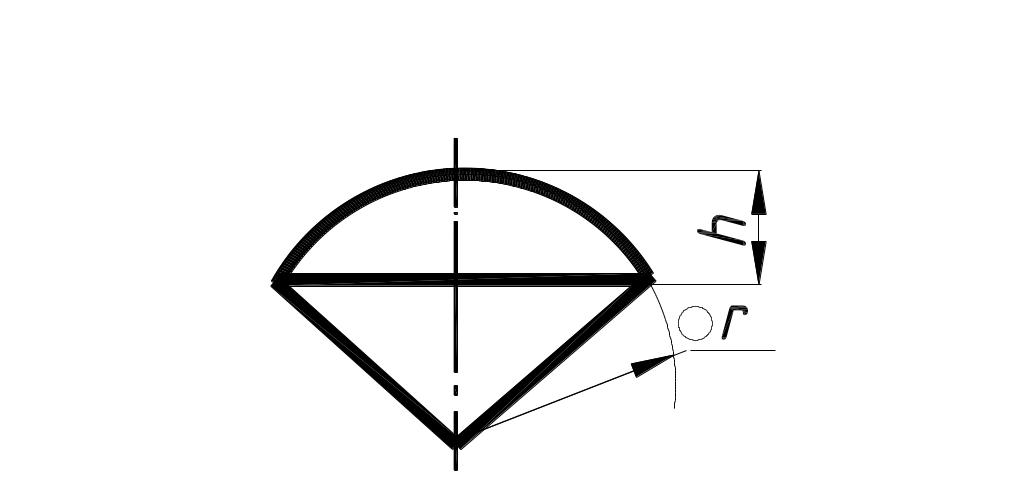
Площадь сегмента
S_сег.
определится
как разность площади сектора с углом α
и площади треугольника

S_сег.=
S_сек.
– S_тр=

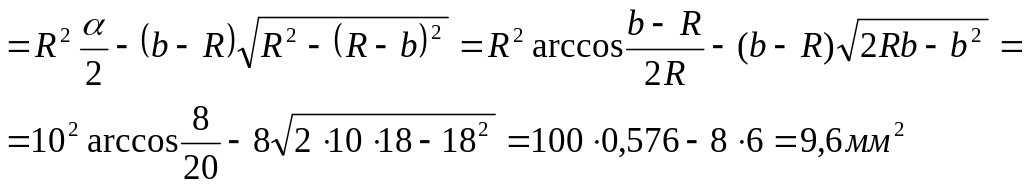
Находим численное
значение объема лыски

V₅
= S_сег.h
= 9,6∙15 = 144
мм³

Рис. 2.5

6. Объем цилиндра
(6)

.

7. Объем цилиндра
(7,8)

,

где р=
1,5 мм
– шаг резьбы.

8. Объем резьбы

V₉
= SLn,

где S=p²tg60^o/4,
L
= 2πr
– длина
витка резьбы, n
= l/p
– количество витков, l
‑ длина резьбы.

Тогда

V₉
= 2πr
p²tg60^o
l/4p
= πr
ptg60^o
l/2
= π5∙1,5∙1,732∙12/2
= 245 мм³

9. Фаска 10:

.

Окончательно,
складываем все объемы, вычитая объем
лыски и шпоночного паза, получим

V₁ + V₂
– V₃ +V₄
– V₅ + V₆
+ V_7,8 + V₉
+ V₁₀
= 160 + 2035,75 – 725,8 + 16,76 -144 + 4712,4 + 3329 + 245 + 63,87
= 9693,8 мм³.

Массу тела получим,
используя ранее приведенную формулу m
= V.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

       
Практическая работа № 3

       
Тема: Расчет
поверхностей

       
Цель работы: Научиться
рассчитывать поверхности «вал» и «отверстие»

          Конструктивно
любая деталь состоит из элементов (поверхностей) различной геометрической
формы, часть из которых взаимодействует с поверхностями других деталей, а
остальная часть элементов является свободной (несопрягаемой). В терминологии по
допускам и посадкам размеры всех элементов деталей независимо от их формы
условно делят на три группы: размеры валов, размеры отверстий и размеры, не
относящиеся к валам и отверстиям.

          
Вал – термин,
условно применяемый для обозначения наружных (охватываемых) элементов деталей,
включая и нецилиндрические элементы, и соответственно сопрягаемых размеров.

          Отверстие
– термин, условно применяемый для обозначения внутренних (охватывающих)
элементов деталей, включая нецилиндрические элементы, и соответственно
сопрягаемых размеров.

           Номинальный размер – размер, относительно которого определяются
предельные размеры и который служит началом отсчета отклонений.

           Действительный размер – размер, установленный измерением с помощью
средства измерений с допускаемой погрешностью измерения.

            Предельные размеры – два
предельно допустимых размера, между которыми должен находиться или которым
может быть равен действительный размер. Больший из двух предельных размеров
называется наибольшим предельным размером, а меньший – наименьшим предельным
размером.

Формулы для расчета предельных размеров:

для отверстия:                                            для
вала:

D_max = D_n
+ ES                                     
   d_max
= d_n +
es

D_min = D_n + EI                                            d_min
= d_n + ei

         Для
упрощения простановки размеров на чертежах вместо предельных размеров
проставляют предельные отклонения:

          верхнее отклонение – алгебраическая разность между наибольшим
предельным и номинальным размерами;

          нижнее отклонение – алгебраическая разность
между наименьшим предельным и номинальным Размерами.

         Верхнее отклонение обозначается ES  для отверстий и
es – для валов; нижнее отклонение обозначается El  для отверстий и ei – для
валов.

         Формулы для расчета отклонений:

         для отверстий:

ES = D_max  – D_n

EI  = D_min  – D_n

           для валов:

es = d_max –  d_n

ei = d_min  –  d_n

Отклонения могут выражаться как в
миллиметрах, так и в микрометрах. 1 мм=1000 мкм_. Отклонения могут
быть со знаками «+» и «-»

           Допуском размера называется разность между наибольшим и
наименьшим предельными размерами или алгебраическая разность между верхним и
нижним отклонениями. Допуск обозначается IT или TD – допуск отверстия и Td –
допуск вала.

         Допуск размера всегда положительная величина.

         Формулы для расчета  допуска:

для отверстия                                                          для
вала

ТD = D_max – D_min = ES –
EI                                    Тd = d_max – d_min = es – ei

Графическое изображение предельных
отклонений, размеров и допуска

           Поле допуска – это поле, ограниченное верхним и нижним
отклонениями. Поле допуска определяется величиной допуска и его положением
относительно номинального размера.

           Нулевой линией называется линия, соответствующая номинальному
размеру, от которой откладываются предельные отклонения размеров при графическом изображении полей допусков. Если нулевая линия расположена
горизонтально, то в условном масштабе положительные отклонения откладываются
вверх, а отрицательные – вниз от нее.

 Порядок
выполнения работы:

1.     
Получить
у преподавателя вариант задания по расчету поверхностей

2.            
Выполнить
расчеты согласно варианта и построить схемы расположения полей допусков

3.           
Ответить
на контрольные вопросы

            Содержание отчета.      

1.   Наименование и цель работы

2.   Решение задач

3.   Ответы на контрольные вопросы

           Контрольные вопросы

1.     Дать
определение поля допуска

2.     Дать
определение вала и отверстия

3.     Какой
размер называется номинальным?

4.     Чем
отличается действительный размер от номинального?

5.     В каких
единицах измерения выражаются отклонения?

6.     Выполните
перевод единиц: 10 мкм = ….. мм;  0,200 мм= … мкм;

205 мкм = …. мм;  
1 мм = ….. мкм.

7.     Дать
определения допуска размера

Варианты заданий по практической ра­боте
3.

Вариант
1

1)Дано: номинальный диаметр вала dн = 2мм
и предельные отклонения es = – 6 мкм; ei = – 12 мкм. Записать условное
обозначение номинального диаметра с предельными отклонениями, определить
предельные размеры, допуск вала. Графически изобразить поле допуска.

2) Дано:
номинальный диаметр вала dн = 270 мм и предельные отклонения es = – 190 мкм; ei
= – 400 мкм. Записать условное обозначение номинального диаметра с предельными
отклонениями, определить предельные размеры, допуск вала. Графически изобразить
поле допуска.

3) Дано: номинальный диаметр
вала dн = 35 мм и предельные отклонения d_max = 35,085
мм; d_min = 35,06 мм. Определить предельные отклонения, допуск вала
и записать условное обозначение номинального размера с предельными
отклонениями. Графически изобразить поле допуска.

Вариант
2

1) Дано: номинальный диаметр
вала dн = 350 мм и предельные отклонения es = – 62 мкм; ei = – 151 мкм.
Записать условное обозначение номинального диаметра с предельными отклонениями,
определить предельные размеры, допуск вала. Графически изобразить поле допуска.

2) Дано: номинальный
диаметр  вала dн = 68 мм и предельные отклонения d_max = 68,050
мм; d_min = 68,020 мм. Определить предельные отклонения, допуск вала
и записать условное обозначение номинального размера с предельными
отклонениями. Графически изобразить поле допуска.

3) Дано: номинальный диаметр вала dн = 630
мм и предельные отклонения es = + 550 мкм; ei = – 550 мкм. Записать условное
обозначение номинального диаметра с предельными отклонениями, определить
предельные размеры, допуск вала. Графически изобразить поле допуска.