Как найти объем валовой продукции матрицы

Постановка
задачи. Пусть
имеется n
отраслей промышленности, каждая из
которых производит продукцию, которая
идет как для внутреннего потребления
данной отраслью и другими отраслями,
так и для конечного личного или
общественного потребления. Обозначим
х_i
– общий
(валовый) объем продукции i-отрасли,
х_ij
– объем
продукции i-отрасли,
потребляемой j-отраслью,
y_i
– объем
конечного продукта i-отрасли.
Имеем соотношение
баланса:

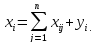
Введем
коэффициенты прямых затрат
.
Если считать, что эти коэффициенты
постоянны в течение некоторого периода
времени, тоx_ij
= a_ij
x_j
, и соотношение баланса примет вид:

или
в матричном виде Х = А٠Х
+ У.

Задача
состоит в
нахождении такого вектора Х, который
при известной матрице прямых затрат А
обеспечивает конечный
продукт
У.

Решая
полученное матричное уравнение, находим
Х = (Е–А)^–1
У.

Матрица
(Е – А)^–1
называется матрицей
полных затрат.

Чтобы
матричное уравнение было разрешимо,
необходимо, чтобы матрица А была
продуктивной.
Есть несколько критериев продуктивности
матрицы. Например, если
максимум сумм элементов столбцов не
более 1 и хоть одна сумма строго меньше
1, то матрица продуктивна.

Пример
1.9. Решение
задачи поиска межотраслевого баланса
[3,
c.
99 – 104].

Имеется
две отрасли производства, в
таблице 1.9
указаны объёмы производства и потребления.

Таблица
1.9

Производство	Потребление	Конечный продукт	Валовый продукт
Энергетика	Машиностроение
Энергетика	100	160	240	500
Машиностроение	275	40	85	400

Необходимо
вычислить объем валового выпуска
продукции каждой отрасли, если конечный
продукт 1-й отрасли должен увеличиться
в 2 раза, 2-й
на
20 %.

Из
таблицы 1.9
имеем:

х₁
= 500, х₂
= 400, у₁
= 240, у₂
= 85, х₁₁
= 100, х₂₁
= 275, х₁₂
=160, х₂₂
= 40.

Построим
матрицу прямых затрат:

а₁₁
=
== 0,2; а₁₂ =
== 0,4;

а₂₁
=
== 0,55; а₂₂
=
== 0,1.

А
=
,
Е–
А =
–
=.

Проверим
матрицу А на продуктивность:

0,2
+ 0,55 = 0,75 < 1, 0,4 + 0,1 = 0,5 < 1, т. е. матрица
А продуктивна.

Найдем
обратную к ней. Вычислим определитель:

0,8٠0,9
– 0,55٠
0,4
= 0,5.

Тогда,

Вычислим
по данным условия задачи новый вектор
конечного продукта
У = (У₁,
У₂):

У₁
= 240٠2
= 480, У₂
= 85 ٠(1+
0,2) = 102. Имеем У_нов
=

Тогда
Х =
=.

1.15.
В таблице
1.10 приведены
данные об исполнении баланса за отчетный
период в усл. ден. ед.

Таблица
1.10

Отрасль	Потребление	Конечный продукт	Валовый продукт
Сфера обслуживания	Лёгкая промышленность
Произ-водство	Сфера обслуживания	7	21	72	100
Лёгкая пром-ть	12	15	63	100

Вычислить
необходимый объем валового выпуска
каждой отрасли, если конечное потребление
сферы обслуживания увеличится вдвое,
а лёгкой промышленности сохранится на
прежнем уровне.

1.16.
Продуктивна ли матрица А:

1)
2).

1.17.
Экономика разделена на три отрасли. В
таблице 1.11
заданы коэффициенты прямых затрат и
конечная продукция отраслей.

Таблица
1.11

Отрасль	Потребление	Конечный продукт
Сфера обслуживания	Лёгкая промышленность	Сельское хозяйство
Произ-водство	Сфера обслуживания	0,3	0,25	0,2	56
Лёгкая промышленность	0,15	0,12	0,03	20
Сельское хозяйство	0,1	0,05	0,08	12

Найти
объем валовой продукции каждой отрасли,
межотраслевые поставки, чистую продукцию
отраслей.

1.18.
Дана матрица полных затрат

Найти
приращение валового выпуска ∆Х,
обеспечивающее приращение конечной
продукции ∆У = (10, 30, 20).

1.19.
Отрасль состоит из 4-х предприятий;
вектор выпуска продукции и матрица
внутреннего потребления имеют вид:

Х
=
А =

Пользуясь
моделью Леонтьева, найти вектор объемов
конечного продукта, предназначенного
для реализации вне отрасли.

1.20.
Данные баланса трех отраслей промышленности
за некоторый промежуток времени даны
в таблице
1.12.
Требуется найти объем валового выпуска
каждого вида продукции, если конечное
потребление увеличить соответственно:

1)
до 60, 70 и 30 единиц;

2)
на 30, 10 и 50 %.

Решить
задачу методом обратной матрицы.

Таблица
1.12

№ п/п	Отрасль	Потребление отрасли	Конечный продукт	Валовый выпуск
1	2	3
1	Добыча и переработка углеводородов	5	35	20	40	100
2	Энергетика	10	10	20	60	100
3	Машиностроение	20	10	10	10	50

Соседние файлы в папке ПОСОБИЯ

• #
• #

  20.03.201612.93 Mб33Уч. пособие по математике (Кремер).pdf

Межотраслевой баланс

С помощью сервиса в онлайн режиме можно:

• найти коэффициенты полных материальных затрат, определить вектор валовой продукции;
• составить межотраслевой баланс, составить схему межотраслевого баланса труда;
• проверить продуктивность матрицы.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.

Система уравнений X = AX + Y называется экономико-математической моделью межотраслевого баланса (МОБ) или моделью «затраты – выпуск». C помощью нее можно выполнить следующие расчеты:

1. подставив в модель объемы валовой продукции каждой отрасли X_i, можно определить объем конечной продукции отрасли Y_j: Y = (E – A)X
2. задав величины конечной продукции всех отраслей Y_j, можно определить величины валовой продукции каждой отрасли X_i: X = (E – A) -1 Y
3. установив для ряда отраслей величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти объемы конечной продукции первых отраслей и объемы валовой продукции вторых.

Здесь A – матрица прямых затрат, коэффициенты которой, a_ij показывают затраты i-й отрасли на производство единицы продукции j-й отрасли. Введем обозначение B = (E – A) -1 . Матрица B называется матрицей полных материальных затрат, коэффициенты которой, b_ij показывают полный объем продукции i-й отрасли, используемой для производства единицы продукции j-й отрасли. С учетом линейности соотношений эффект распространения спроса ΔX, вызванный изменением конечного спроса на величину ΔY рассчитывается как: ΔX = B·ΔY
Через C=A-B обозначают матрицу косвенных затрат.

Пример №1 . Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат A и вектор конечной продукции Y .

Пример №2 . Дан межотраслевой баланс трехотраслевой модели хозяйства:

№ отрасли потребления	1	2	3	Конечный продукт	Валовый продукт	Y’
№ отрасли	1	20	20	60	100	200	150
отрасли	2	20	40	60	80	200	100
производства	3	20	0	10	70	100	100

Определить:
1) технологическую матрицу;
2) матрицу коэффициентов полных затрат;
3) дать экономический анализ каждого столбца матрицы коэффициентов полных затрат;
4) определить валовый выпуск X’ на новый ассортимент конечной продукции Y’;

Решение.
Находим валовой объем продукции x_i;
x₁ = 20 + 20 + 60 + 100 = 200
x₂ = 20 + 40 + 60 + 80 = 200
x₃ = 20 + 0 + 10 + 70 = 100

Отрасль	Потребление	Конечный продукт	Валовой выпуск
Производство	20	20	60	100	200
20	40	60	80	200
20	0	10	70	100

По формуле a_ij = x_ij / x_j находим коэффициенты прямых затрат:
a₁₁ = 20/200 = 0.1; a₁₂ = 20/200 = 0.1; a₁₃ = 60/100 = 0.6; a₂₁ = 20/200 = 0.1; a₂₂ = 40/200 = 0.2; a₂₃ = 60/100 = 0.6; a₃₁ = 20/200 = 0.1; a₃₂ = 0/200 = 0; a₃₃ = 10/100 = 0.1;

0.1	0.1	0.6
0.1	0.2	0.6
0.1	0	0.1

Определим матрицу коэффициентов полных затрат с помощью формул обращения невырожденных матриц.
а) Находим матрицу (E-A):

(E-A) =

0,9 -0,1 -0,6 -0,1 0,8 -0,6 -0,1 0 0,9

б) Вычисляем обратную матрицу (E-A) -1 :

Найдем величины валовой продукции трех отраслей

X’ = (B -1 *Y’) =

1,23 0,15 0,92 0,26 1,28 1,03 0,14 0,0171 1,21

*

=

Пример №3 . В модели межотраслевого баланса

Производство	Потребление	Конечная продукция	Валовая продукция
1	2	3
1	10	5	15	70	100
2	20	…	…	…	…
3	30	…	…	…	…
Оплата труда	30	…	…	…	…
Прибыль D	D	…	…	…	…

прибыль D равна:
D = Валовая продукция – Затраты на производство – Оплата труда = 100 – (10+20+30) – 30 = 10.

2 Дана матрица прямых затрат A = Найти а) вектор валовой продукции X для обеспечения выпуска конечной продукции Y= Решение

2. Дана матрица прямых затрат A = .
Найти: а) вектор валовой продукции X для обеспечения выпуска конечной продукции Y=
Решение:
A = – матрица прямых затрат имеет неотрицательные элементы и удовлетворяет критериям продуктивности.
Поэтому для любого вектора конечного продукта Y можно найти необходимый объем валового выпуска X по формуле 1.
X= (E-A)-1*Y
Где (E-A)-1=B – матрица полных материальных затрат
Найдем B:
E-A= -=

Так как определитель матрицы
= 0,9*0,8-0,5*0,3=0,72-0,15=0,57>0, определитель отличен от нуля, имеет обратную матрицу и притом только одну

B= (E-A)-1=
По условию задачи Y=
Тогда X= = * =
б) приращение вектора ∆ для увеличения выпуска конечной продукции на ∆Y= .
Решение:
С учетом линейности соотношений эффект распространения спроса ∆ вызванный изменением конечного спроса на величину ∆Y рассчитаем как
∆ =B*∆Y
∆ = *
∆ = *
∆ = =

0104OLV 4.7

Преподаватель высшей школы менеджмента Преподаватель английского языка высшей категории

(новое) МЕЖОТРАСЛЕВОЙ БАЛАНС В таблице представлены данные отчетного межотраслевого баланса (МОБ) в стоимостном выражении по отраслям (N-номер варианта) Производящие отрасли Потребляющие отрасли Конечный продукт (Y) Валовой продукт (X) Пр-ть С/х Проч Промышленность 400+2N 200+N 150+N 800+2N

(новое)
МЕЖОТРАСЛЕВОЙ БАЛАНС

В таблице представлены данные отчетного межотраслевого баланса (МОБ) в стоимостном выражении по отраслям (N-номер варианта)

Производящие
отрасли Потребляющие отрасли Конечный продукт (Y) Валовой
продукт (X)

Промышленность 400+2N 200+N 150+N 800+2N ?
Сельское хоз-во 250+N 100 50 ? 600+2N
Прочие отрасли ? 50+N 50 150 350+N
Требуется:
Найти недостающие величины и заполнить шахматную таблицу МОБ.
Определить коэффициенты прямых материальных затрат.
Определить коэффициенты полных материальных затрат.
Найти вектор валового выпуска из соотношения и сравнить его с валовым продуктом отраслей, представленных в таблице.
Предполагая неизменность коэффициентов прямых затрат, определить вектор валового продукта отраслей в плановом периоде, если установлены следующие темпы прироста конечной продукции: промышленность – 10%, С/Х – 5%, прочие отрасли 3%.
По результатам, выполненным в п. 5 расчетов, определить производственное потребление продукции в плановом периоде. Заполнить таблицу МОБ.

1. Найти недостающие величины и заполнить шахматную таблицу МОБ.
Производящие
отрасли Потребляющие отрасли Конечный продукт (Y) Валовой
продукт (X)

Промышленность 442 221 171 842 1676
Сельское хоз-во 271 100 50 221 642
Прочие отрасли 100 71 50 150 371

2. Определить коэффициенты прямых материальных затрат.

По формуле aij = xij / xj находим коэффициенты прямых затрат:

a11 = 442/1676 = 0.264; a12 = 221/642 = 0.344; a13 = 171/371 = 0.461; a21 = 271/1676 = 0.162; a22 = 100/642 = 0.156; a23 = 50/371 = 0.135; a31 = 100/1676 = 0.0597; a32 = 71/642 = 0.111; a33 = 50/371 = 0.135;

0.264 0.344 0.461
0.162 0.156 0.135
0.0597 0.111 0.135

Коэффициент прямых затрат (aij) показывает, какое количество продукции i-й отрасли необходимо, учитывая только прямые затраты, для производства единицы продукции j-й отрасли.

3. Определить коэффициенты полных материальных затрат.
I. Определим матрицу коэффициентов полных материальных затрат приближенно, учитывая косвенные затраты до 2-го порядка включительно.
а) Матрица коэффициентов косвенных затрат 1-го порядка равна:
EQ A(1) = A2 = b(a al co3 hs3 (0,264;0,344;0,461;0,162;0,156;0,135;0,0597;0,111;0,135)) • b(a al co3 hs3 (0,264;0,344;0,461;0,162;0,156;0,135;0,0597;0,111;0,135)) = b(a al co3 hs3 (0,153;0,195;0,23;0,0759;0,0948;0,114;0,0417;0,0527;0,0606))
б) Матрица коэффициентов косвенных затрат 2-го порядка равна:
EQ A(2) = A3 = b(a al co3 hs3 (0,264;0,344;0,461;0,162;0,156;0,135;0,0597;0,111;0,135)) • b(a al co3 hs3 (0,153;0,195;0,23;0,0759;0,0948;0,114;0,0417;0,0527;0,0606)) = b(a al co3 hs3 (0,0856;0,108;0,128;0,0421;0,0535;0,0631;0,0231;0,0292;0,0345))
Матрица коэффициентов полных затрат приближенно равна:
EQ B = E + A + A2 + A3 = b(a al co3 hs3 (1,502;0,648;0,819;0,28;1,304;0,312;0,124;0,193;1,23))
II. Определим матрицу коэффициентов полных затрат B-1 с помощью формул обращения невырожденных матриц.
Коэффициент полных затрат (bij) показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.
Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства продукции.

а) Находим матрицу (E-A):
EQ (E-A) = b(a al co3 hs3 (0,736;-0,344;-0,461;-0,162;0,844;-0,135;-0,0597;-0,111;0,865))

б) Вычисляем обратную матрицу (E-A)-1:
Запишем матрицу в виде:
EQ b(a al co3 hs3 (0,736;-0,344;-0,461;-0,162;0,844;-0,135;-0,0597;-0,111;0,865))
Главный определитель
∆=0.74•(0.84•0.87-(-0.11•(-0.13)))-(-0.16•(-0.34•0.87-(-0.11•(-0.46))))+(-0.0597•(-0.34•(-0.13)-0.84•(-0.46)))=0.44445833768381
Определитель отличен от нуля, следовательно матрица является невырожденной и для нее можно найти обратную матрицу A-1.
Транспонированная матрица.
EQ BT=b(a al co3 hs3 (0,736;-0,162;-0,0597;-0,344;0,844;-0,111;-0,461;-0,135;0,865))
Найдем алгебраические дополнения матрицы BT.
EQ BT1,1=(-1)1+1bbc|(a al co2 hs2 (0,844;-0,111;-0,135;0,865))
∆1,1=(0.84•0.87-(-0.13•(-0.11)))=0.71555366989487
EQ BT1,2=(-1)1+2bbc|(a al co2 hs2 (-0,344;-0,111;-0,461;0,865))
∆1,2=-(-0.34•0.87-(-0.46•(-0.11)))=0.34881729376729
EQ BT1,3=(-1)1+3bbc|(a al co2 hs2 (-0,344;0,844;-0,461;-0,135))
∆1,3=(-0.34•(-0.13)-(-0.46•0.84))=0.43551569761905
EQ BT2,1=(-1)2+1bbc|(a al co2 hs2 (-0,162;-0,0597;-0,135;0,865))
∆2,1=-(-0.16•0.87-(-0.13•(-0.0597)))=0.147944020402
EQ BT2,2=(-1)2+2bbc|(a al co2 hs2 (0,736;-0,0597;-0,461;0,865))
∆2,2=(0.74•0.87-(-0.46•(-0.0597)))=0.60954719061197
EQ BT2,3=(-1)2+3bbc|(a al co2 hs2 (0,736;-0,162;-0,461;-0,135))
∆2,3=-(0.74•(-0.13)-(-0.46•(-0.16)))=0.17375633691487
EQ BT3,1=(-1)3+1bbc|(a al co2 hs2 (-0,162;-0,0597;0,844;-0,111))
∆3,1=(-0.16•(-0.11)-0.84•(-0.0597))=0.068254224448509
EQ BT3,2=(-1)3+2bbc|(a al co2 hs2 (0,736;-0,0597;-0,344;-0,111))
∆3,2=-(0.74•(-0.11)-(-0.34•(-0.0597)))=0.1019654415389
EQ BT3,3=(-1)3+3bbc|(a al co2 hs2 (0,736;-0,162;-0,344;0,844))
∆3,3=(0.74•0.84-(-0.34•(-0.16)))=0.56593079543759
Обратная матрица.
EQ B-1=f(1;0.44445833768381)b(a al co3 hs3 (0,716;0,349;0,436;0,148;0,61;0,174;0,0683;0,102;0,566))
Матрица коэффициентов полных затрат равна:
EQ B-1=b(a al co3 hs3 (1,61;0,785;0,98;0,333;1,371;0,391;0,154;0,229;1,273))

4. Найти вектор валового выпуска из соотношения и сравнить его с валовым продуктом отраслей, представленных в таблице.

EQ X = (B-1•Y) = b(a al co3 hs3 (1,61;0,785;0,98;0,333;1,371;0,391;0,154;0,229;1,273)) • b(a al co1 hs3 (842;221;150)) = b(a al co1 hs3 (1676;642;371))
Найденный вектор валового выпуска совпадает с валовым продуктом отраслей, представленных в таблице

5. Предполагая неизменность коэффициентов прямых затрат, определить вектор валового продукта отраслей в плановом периоде, если установлены следующие темпы прироста конечной продукции: промышленность – 10%, С/Х – 5%, прочие отрасли 3%.

Для расчета планового валового выпуска по формуле X =B*Y необходимо вычислить плановый конечный продукт увеличив отчетный по каждой отрасли на 10, 5 и 3 % соответственно.
Получим:

Отчетный конечный продукт

Новый конечный продукт

842 926,2
221 232,05
150 154,5

Плановый валовой продукт получим по формуле X =B*Y

1824,75
686,97
392,45

6. По результатам, выполненным в п. 5 расчетов, определить производственное потребление продукции в плановом периоде. Заполнить таблицу МОБ

Этот результат помещаем в столбце «Вал. продукт» таблицы планового баланса. Для заполнения «шахматки» воспользуемся формулой xij = aij*xj , а далее – как при заполнении таблицы отчетного баланса. После соответствующих вычислений получим таблицу
Таблица планового МОБ

Производящие
отрасли Потребляющие отрасли Конечный продукт (Y) Валовой
продукт (X)

Промышленность 487,734 236,31768 180,91945 926,2 1824,75
Сельское хоз-во 295,488 107,16732 52,98075 232,05 686,97
Прочие отрасли 108,9376 76,25367 52,98075 154,5 392,45

Список использованной литературы

1. Бушин П. Я., Захарова В. Н. Математические методы и модели в экономике: учеб. пособие. – Хабаровск, 1998.
2. Бушин П. Я. Математические модели в управлении: учеб. пособие. – Хабаровск, 1999.
3. Колемаев В. А. Математическая экономика: Учебник для вузов.- М., 2002.- 304 с.
4. Кузнецов Ю. А., Кузубов В. Н., Волощенко А. В. Математическое программирование. – М. : Высшаяшкола, 1980.
5. Леонтьев В.В. Межотраслевая экономика М ,1997. -315 с

[spoiler title=”источники:”]

[/spoiler]

Задача

Экономика
представлена двумя отраслями производства: промышленностью и сельским
хозяйством. За отчетный период получены следующие данные о межотраслевых
поставках

 и векторе объемов конечного использования

.

Требуется:

Указание:
При вычислениях производить округление с точностью до тысячных.

Решение

Матрица прямых затрат

Найдем
валовые выпуски отраслей, просуммировав в каждой строке межотраслевые поставки
и координату вектора

:

Найдем
матрицу прямых затрат. Ее элементы можно найти по формуле:

Подставляя
числовые значения, получаем:

Матрица «Затраты – выпуск»

Найдем матрицу
«Затраты – выпуск»

Вектор конечного использования Y для валового объема выпуска X

Вектор
конечного использования Y для валового объема выпуска X определим на основе
балансового соотношения: 

Для этого выполним умножение двух матриц

Матрица полных затрат

Найдем
матрицу коэффициентов полных материальных затрат

 -она будет равна обратной матрице

:

Определитель матрицы

:

Алгебраические
дополнения:

Обратная матрица:

Вектор валового объема выпуска X для конечного использования Y

Вектор валового объема выпуска

 для конечного продукта

 определим формуле:

Приросты валовых объемов выпуска

Найдем
приросты валовых объемов выпуска, если конечное потребление должно изменяться
на

 по сравнению с

:

Матрица полных затрат ресурсов S

Найдем
матрицу полных затрат ресурсов S для заданной матрицы ее прямых затрат M:

Суммарная потребность в ресурсах

Суммарная  потребность в ресурсах для вектора Y₀:

Суммарная  потребность в ресурсах для вектора Y_n:

Матрицы косвенных затрат и сумма затрат

Найдем
матрицы косвенных затрат первого, второго и третьего порядка

Сумма затрат:

Разность
матриц:

Вектор потребности в продукции

Найдем
вектор потребности в продукции всех отраслей материального производства b_ij
для получения единицы конечного продукта b_j вида. Для этого
просуммируем столбцы матрицы полных затрат:

Это значит, что для производства
единицы конечного продукта в первой отрасли во всех отраслях надо расходовать
продукции на сумму 1,913 ден.ед., для производства единицы конечного продукта
во второй отрасли -на 2,021 ден.ед.

          

Номер задачи: Mme-21

Решение: бесплатно

Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени. Взаимодействие отраслей определяется матрицей А прямых затрат.

Число а_ij, стоящее на пересечении i-й строки и j-го столбца, равно x_ij/x_j,

где

x_ij – поток средств производства из i-й отрасли в j-ю,

x_j – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости).

Задан вектор  объемов продуктов конечного потребления.

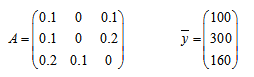
• определить, является ли матрица А продуктивной;

• составить уравнение межотраслевого баланса;

• найти объемы валовой продукции каждой отрасли .

• составить матрицу потоков средств производства (x_ij);

• найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.